Cryptography Lecture 12 Arpita Patra Arpita Patra Recall

Cryptography Lecture 12 Arpita Patra © Arpita Patra

Recall - If PRG exists, then so does PRF o Construction of PRF using PRG o Introduction to Hybrid Proof Technique o Proof

Today’s Goal - One-way Functions (OWF) & One-way Permutations (OWP) o Definition o Do they exist? o Candidate OWF o Recall def. of PRG, PRF. Which out of the three looks simpliest - Hard-core Predicates of OWF/OWP o Definition o Non-triviality of finding it. o Hard-core predicates from OWF/OWP (Goldreich-Levin Theorem) – partial proof - Roadmap of constructing PRG for poly expansion factor from OWF + Hard-core predicate

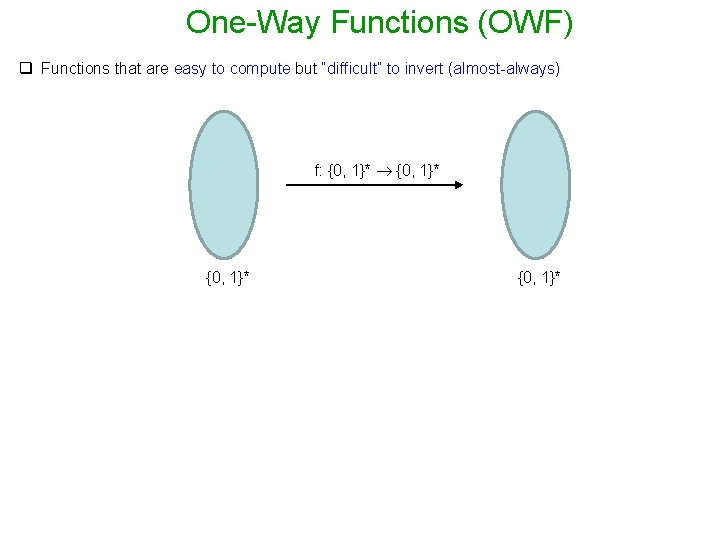
One-Way Functions (OWF) q Functions that are easy to compute but “difficult” to invert (almost-always) f: {0, 1}*

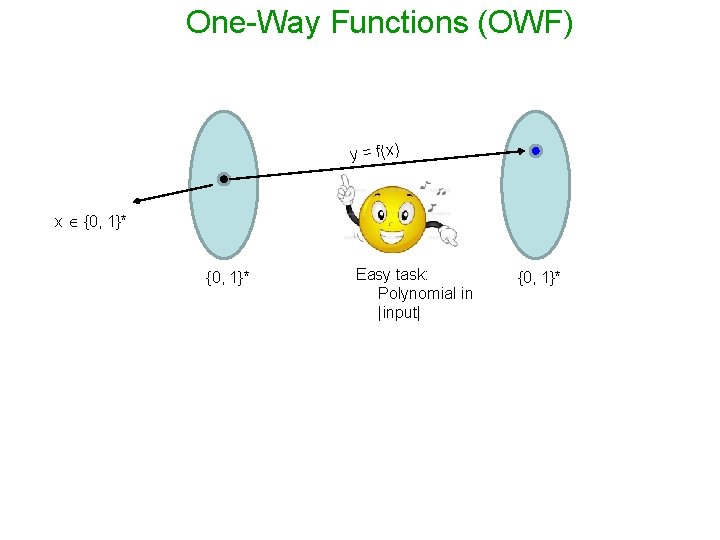
One-Way Functions (OWF) y = f(x) x {0, 1}* Easy task: Polynomial in |input| {0, 1}*

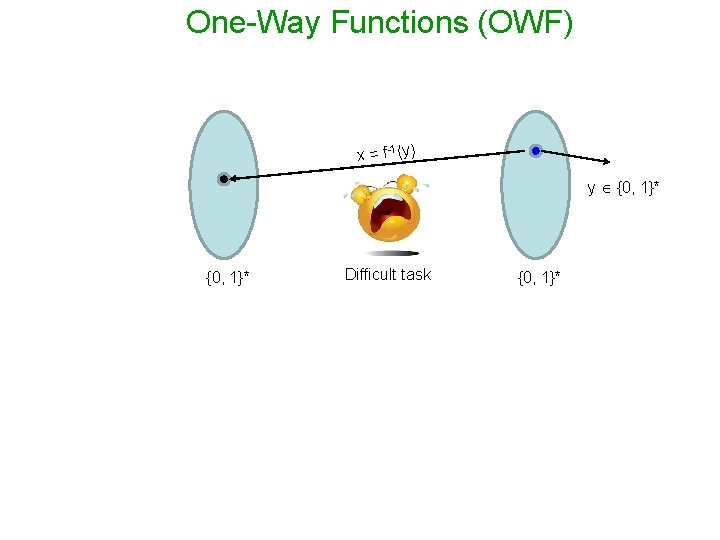
One-Way Functions (OWF) x = f-1 (y) y {0, 1}* Difficult task {0, 1}*

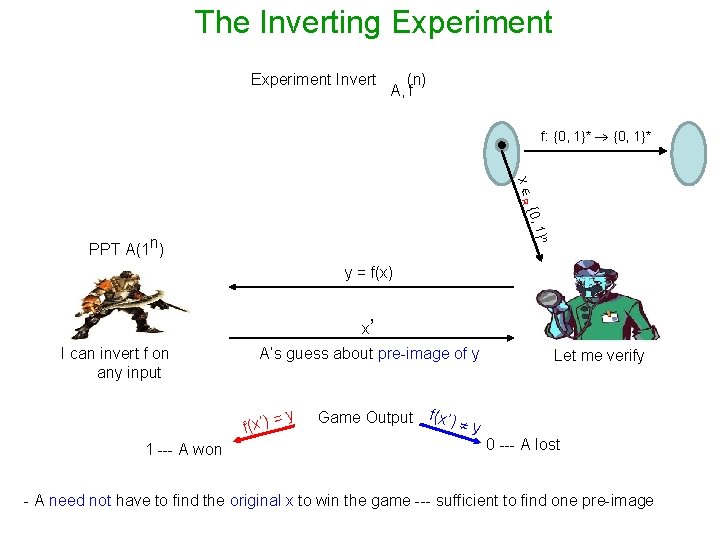
The Inverting Experiment Invert (n) A, f f: {0, 1}* x R {0, 1 }n PPT A(1 n) y = f(x) x’ I can invert f on any input A’s guess about pre-image of y f(x’) = 1 --- A won y Game Output f(x’) y Let me verify 0 --- A lost - A need not have to find the original x to win the game --- sufficient to find one pre-image

OWF: Mathematical Formulation f: {0, 1}* Function f is a OWF if the following two conditions hold : - Easy to compute: for every x {0, 1}*, f(x) can be computed in poly(|x|) times - Hard to Invert: For every PPT algorithm A, there is a negligible function negl() : Pr Invert (n) A, f = 1 negl(n) Pr [ A(f(x), 1 n) f-1(f(x))] negl(n) x {0, 1}n q OWF does not exist in the realm of unbounded powerful adversary. - Any function is invertible in principle given enough time/computational power. - The assumption of existence of OWF is about computational hardness.

Functions that are not one-way (non-OWFs) Pr Invert = 1 negl(n) A, f Pr [ A(f(x), 1 n) f-1(f(x))] negl(n) x {0, 1}n For a function to be non-OWF, there should exist an A, p(n) s. t x {0, 1}n Example I: Consider f s. t. Pr [ A(f(x), 1 n) f-1(f(x))] x {0, 1}n 3/4 f is not one-way Example III: f(x) = x 1 x 2……xn-1, where x {0, 1}n Pr [ A(f(x), 1 n) f-1(f(x))] = 1/2 x {0, 1}n > 1/n 10 when n is even negl(n) when n is odd Example II: f(x, y) = x. y, where x, y N Pr [ A(f(x, y), 1 n) f-1(f(x, y))] x, y {0, 1}n/2 f is not one-way

Do OWFs Exist? q No unconditional proof of their existence yet. - Proof is hard because - Finding a proof will lead to solving the million dollar question in CS whether P = NP or not q Whole world believes that they do and so existence of OWF is an assumption/conjecture - Several noteworthy computational problems (int. factorization) received intensive attention since ages (even before crypto was born) but no poly time algo is found. > The former suggests every PPT algo must fail to solve at least for one input > The latter suggests every PPT algo must fail to solve ALMOST ALWAYS (for any random input) - Being NP-complete is not enough to be a candidate OWF - Belief that OWF exists is much more than believing P NP

Candidate OWFs q Subset Sum Problem: q Integer Factorization: f(x, y) = xy : x and y are equal length primes.

One-Way Permutation (OWP) f: {0, 1}* q Function f is length-preserving if |f(x)| = |x| for all x Ø Size of the image and pre-image are the same q Function f is a OWP if it it is a OWF and Ø Length-preserving Ø One-to-one mapping q If f is a OWP then every y has a unique pre-image x Ø Still finding x should be hard in polynomial time {0, 1}*

Hard-Core Predicates q Let f: {0, 1}* be a OWF - Given y = f(x) for a random x, computing the entire x is hard - Does this mean nothing about x can be determined from f(x) ? q Given f, define g as follows: - g(x 1, x 2) = (x 1, f(x 2)), where |x 1| = |x 2| - g too is OWF (otherwise inverter of g can be used to invert f) !! - but it leaks half of its input !! q In general, f(x) does NOT hide everything about x. q But, f(x) must hide something about x (otherwise computing x would have been easy) - “something” that remains hidden about x even given f(x) is captured by hard-core predicates - They are one bit of info about x that is hard to guess given f(x). - Modelled as a Boolean function: hc: {0, 1}* {0, 1}

Hard-Core Predicates - Let f: {0, 1}* be ANY function (need not be a OWF) - Let hc: {0, 1}* {0, 1} be a Boolean function Function hc is a hard-core predicate for the function f if the following holds: - Given x, the value hc(x) can be computed in polynomial (in input size) time - Pr [ A(f(x), 1 n) = hc(x)] ½ + negl(n) x {0, 1}n q Hard-core Predicate may exist even for functions that are NOT one-way - Non-OWF: f(x 1, …, xn) = (x 1, …, xn-1) - hc(x 1, …, xn) = xn - For a RANDOM x, given f(x 1, …, xn), hc(x 1, …, xn) can be guessed with prob. ½ q We are NOT interested in hard-core predicates of functions that are NOT one-way.

Hard-Core Predicates for Permutations - Let f: {0, 1}* be a permutation - Let hc: {0, 1}* {0, 1} be a Boolean function Function hc is a hard-core predicate for the permutation f if the following holds: - Given x, the value hc(x) can be computed in polynomial (in input size) time - Pr [ A(f(x), 1 n) = hc(x)] ½ + negl(n) x {0, 1}n q Does hardcore predicates exist for permutations that are not one-way - Not possible CT 16 (one): If a one-to-one function has hard-core predicate then it must be one-way.

Finding HCPs for OWF/OWP is not Simple q Let f: {0, 1}* be a OWF - Given f(x 1, …, xn) for a random x = x 1, …, xn, at least one of the bits of x must be hidden --- as f is a OWF - So computing x 1 … xn from f(x 1, …, xn) must be hard - So hc(x 1, …, xn) = x 1 … xn is a hard-core predicate for f q Consider g constructed using f - g(x 1, …, xn) = (f(x 1, …, xn), x 1 … xn) - g is a OWF (else f is not a OWF; proof by reduction) - hc(x) = x 1 … xn is not a HCP for g q For a given fixed Boolean function hc(x), there always exist a OWF f such that hc is not a hard-core predicate for the function f

Does HCP exist for any OWF? q No proof yet. q Given a OWF f, we can construct a OWF g and its HCP. Weaker yet sufficient for our purpose Theorem (Goldreich-Levin): Assume OWF (OWP) exists, then there exists a OWF (OWP) g and a hard-core predicate hc for g. - Let f be a OWF/OWP - g(x, r) = (f(x), r), where x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn is a hard-core predicate for the function g Theorem (Goldreich-Levin): Let f be a OWF/OWP and define g by g(x, r) = (f(x), r), where x = x 1, …, xn and r = r 1, …, rn. Then the Boolean function hc(x, r) = r 1 x 1 … rnxn is a hard-core predicate for the function g

Roadmap PRF OWF/P g, hc OWF/P f

Goldreich Levin Theorem (Goldreich-Levin): Let f be a OWP and define g by g(x, r) = (f(x), r), where x = x 1, …, xn and r = r 1, …, rn. Then the Boolean function hc(x, r) = r 1 x 1 … rnxn is a hard-core predicate for the function g A A’ Proof: Difficulty Level ***** x {0, 1}n Pr[A’(f(x)) = x))] = 1 x, r {0, 1}n *** * x, r {0, 1}n Pr[A(f(x), r) = hc(x, r)] = 1

GL Theorem: The Most Simple Case (*) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn Pr[A’(f(x)) = x))] = 1 Pr[A(f(x), r) = hc(x, r)] = 1 A A’ f(x 1, …, xn), (1, 0, …, 0) Aha! x 1 Aha! x 2 x 1, …, xn Aha! xn x 1 0 … 0 f(x 1, …, xn), (0, 1, …, 0) 0 x 2 … 0 f(x 1, …, xn), (0, 0, …, 1) 0 0… xn

GL Theorem: The Most Simple Case (*) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn Why 1: guarantee t o n s e o D rrect for o c e r a s c the h it always e b y a m ; sure 0) , 0 , … , 0 , 1 ( fails for r= x, r {0, 1}n x {0, 1}n A’ f(x 1, …, xn) Aha! x 1 Aha! x 2 Why 2: r can Adv’s powe en queried h w d e v ie tr f(xre 1, …, xn), m(1, 0) re r’s he…, r (0, o d n a r n o ndom) ot 0 ra… arex n 0 1 f(x 1, …, xn), (0, 1, …, 0) 0 x 2 … 0 f(x 1, …, xn), (0, 0, …, 1) x 1, …, xn Aha! xn 0 0… xn A

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn x, r {0, 1}n x {0, 1}n A’ f(x 1, …, xn) A f(x 1, …, xn), r = (r 1, r 2, …, rn) x 1 r 1 … xn rn The r’s in both are random (but not f(x 1, …, xn), r (1, 0, …, 0) independent)! x 1 r’ 1 … xn rn Aha! x 1 Aha! xi -> Flip the ith bit in the second query But we are not sure if in both the queries returned hcs are correct.

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn Lemma: If n be such that x, r {0, 1}n A’ f(x 1, …, xn) A f(x 1, …, xn), r = (r 1, r 2, …, rn) x 1 r 1 … xn rn The r’s in both are random (but not f(x 1, …, xn), r (1, 0, …, 0) independent)! x 1 r’ 1 … xn rn Aha! x 1 Then S Domain of x of length n

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn Theorem: If we have A, p(n) s. t. for infinitely many n’s x, r {0, 1}n Let n be s. t. x, r {0, 1}n Then we can construct A’ s. t. x {0, 1}n Then we have A’ s. t. x {0, 1}n for infinitely many n’s

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn r {0, 1}n Then we can construct A’ s. t. for every x in S Union Bound over n bits Then we can construct A’ s. t. for every x in S x {0, 1}n

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn r {0, 1}n Then we can construct A’ s. t. for every x in S Union Bound over n bits Then we can construct A’ s. t. for every x in S Easy prob. calculation Then we can construct A’ s. t. x {0, 1}n Pr[A’(f(x)) = x))] x {0, 1}n x {0, 1}n = 1/4 p(n)

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn r {0, 1}n Prob. Boosting/Amplification technique Then we can construct A’ s. t. for every x in S Union Bound over n bits Then we can construct A’ s. t. for every x in S Easy prob. calculation Then we can construct A’ s. t. x {0, 1}n Pr[A’(f(x)) = xi] = r {0, 1}n -m/2(p(n))2 (Chernoff Bound) Find m from e -m/2(p(n))2 = 1/2 n Repeat m times (w. r. t random r) and take majority

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn x {0, 1}n r {0, 1}n A’ A f(x 1, …, xn), r = (r 1, r 2, …, rn) x 1 r 1 … xn rn f(x 1, …, xn), r (1, 0, …, 0) x 1 r’ 1 … xn rn Aha! x 1, …, xn Find x 1 and take majority Repeat m times with random r Repeat for each i

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn Theorem: If we have A, p(n) s. t. for infinitely many n’s x, r {0, 1}n Let n be s. t. x, r {0, 1}n Why ¾ will be clear here. r {0, 1}n Then we can construct A’ s. t. x {0, 1}n Then we have A’ s. t. Pr[A’(f(x)) = x] ≥ 1/4 p(n) x {0, 1}n for infinitely many n’s

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn Let n be s. t. x, r {0, 1}n Why ¾ clear ? Union Bound & Easy prob. calculation r {0, 1}n r {0, 1}n

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn Let n be s. t. x, r {0, 1}n (moderately) Easy prob. calculation r {0, 1}n Union Bound & Easy prob. calculation r {0, 1}n Pr[A(f(x), r) = hc(x, r)] x, r {0, 1}n r {0, x 1}n r {0, 1}n r {0, 1}n

GL Theorem: The Moderately Simple Case (***) - g(x, r) = (f(x), r), x = x 1, …, xn and r = r 1, …, rn. - hc(x, r) = r 1 x 1 … rnxn Theorem: If we have A, p(n) s. t. for infinitely many n’s x, r {0, 1}n Let n be s. t. x, r {0, 1}n Then we can construct A’ s. t. x {0, 1}n Then we have A’ s. t. Pr[A’(f(x)) = x] ≥ 1/4 p(n) x {0, 1}n for infinitely many n’s

Roadmap PRF OWF/P g, hc OWF/P f

CT 17 (one): If f is a OWF, then prove or disprove that g(x) = (f(x), f(f(x))) is a OWF. CT 18 (two): If there exists a PRF that maps n-length key and input to 1 -bit output, then there exists a PRF that maps n 2 -length key and n-bit input to n-bit output CT 19 (one): If G: {0, 1}n+1 is a PRG, then G is a OWF.