Cryptography Lecture 6 Arpita Patra Arpita Patra Recall

Cryptography Lecture 6 Arpita Patra © Arpita Patra

Recall >> Computational security o Security definitions (ind-coa/sem-coa) o Pseudorandom Generators (PRGs), non-trivial to construct, no secure PRG in the face of an unbounded powerful adversary o A scheme based on PRG o Reduction based proof overview, proof of our scheme >> More stronger definition o Mult-coa definition o Stronger than coa and needs randomized encryption scheme

Today’s Goal - Introduction to cpa attack and cpa security - Look for assumption needed to construct a scheme o Pseudo-random Functions o Definition o Non-trivial to construct o Pseudo-random Permutation (Strong/weak variant) - Construction based on PRF

Security for SKE with COA to CPA - - Randomized PPT COA Randomized PPT CPA Given the knowledge of two messages (vector of messages), it cannot be distinguished if the ciphertext corresponds to the first or second message (message vector).

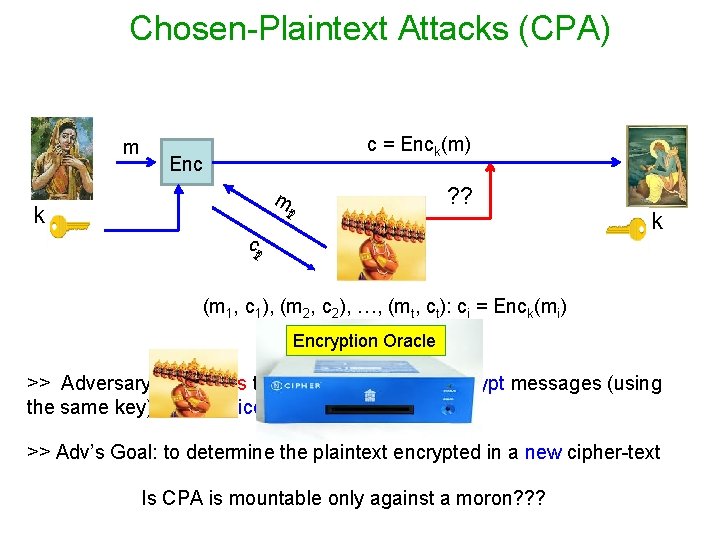
Chosen-Plaintext Attacks (CPA) m c = Enck(m) Enc ? ? m k t 21 ct 21 k (m 1, c 1), (m 2, c 2), …, (mt, ct): ci = Enck(mi) Encryption Oracle >> Adversary influences the honest parties to encrypt messages (using the same key) of its choice >> Adv’s Goal: to determine the plaintext encrypted in a new cipher-text Is CPA is mountable only against a moron? ? ?

CPA M. Luby: Pseudorandomness and Cryptographic Applications; Princeton University Press, 1996 Mihir Bellare, Anand Desai, E. Jokipii, Phillip Rogaway: A Concrete Security Treatment of Symmetric Encryption. FOCS, 1997.

Is CPA Realistic ? q How can an attacker influence parties to encrypt messages of its choice (using the same key) ? q Consider a secure hardware with secret-key embedded >> Often used in military applications q An insider may have access to the hardware (not the key) >> Can choose messages of its choice and get their encryptions

CPA shortened WWII by 2 -3 Years q Break of German codes by British during WW II Allied Power Loc 3 Loc 1 Loc 2 At Bletchley Park Axis Power Enc (L k o q Trivia: Who played a key role in this cryptanalysis process c 1 ) E nck (Lo c 2 ) Enc (L k oc ) 3

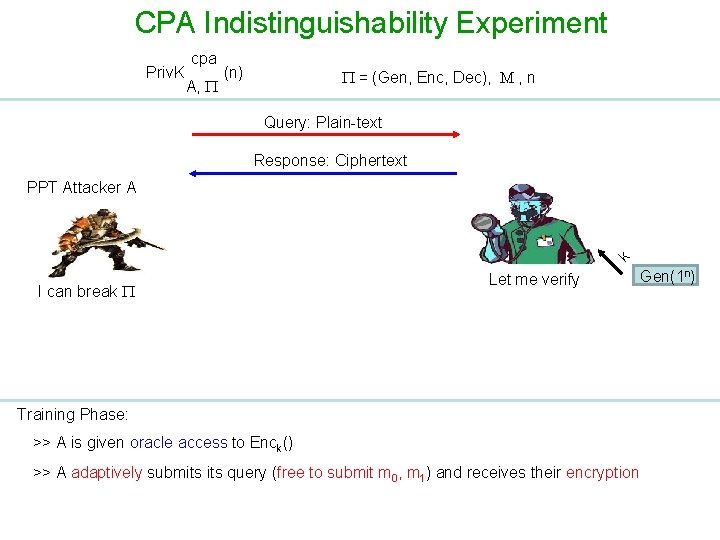
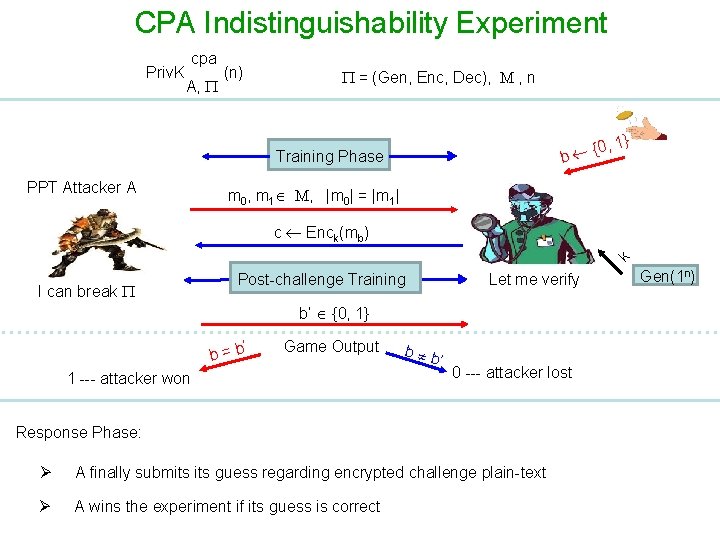
CPA Indistinguishability Experiment Priv. K cpa A, (n) = (Gen, Enc, Dec), M , n Query: Plain-text Response: Ciphertext k PPT Attacker A I can break Let me verify Gen(1 n) Training Phase: >> A is given oracle access to Enck() >> A adaptively submits query (free to submit m 0, m 1) and receives their encryption

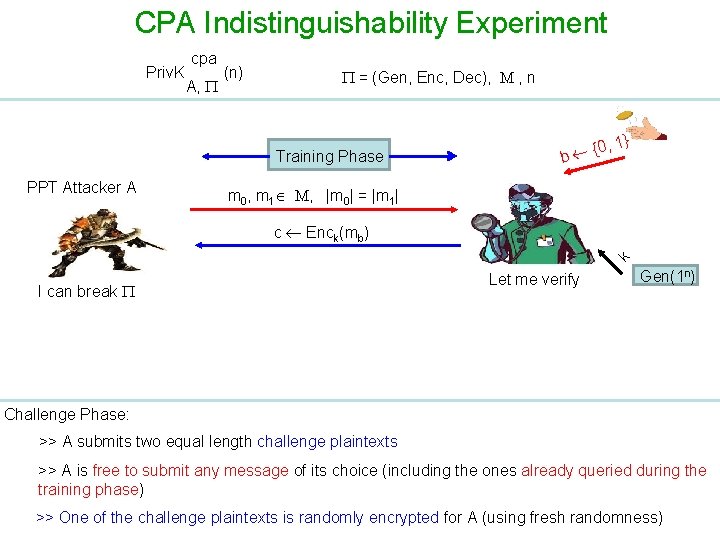
CPA Indistinguishability Experiment Priv. K cpa A, (n) = (Gen, Enc, Dec), M , n Training Phase PPT Attacker A {0 b , 1} m 0, m 1 M, |m 0| = |m 1| k c Enck(mb) I can break Let me verify Gen(1 n) Challenge Phase: >> A submits two equal length challenge plaintexts >> A is free to submit any message of its choice (including the ones already queried during the training phase) >> One of the challenge plaintexts is randomly encrypted for A (using fresh randomness)

CPA Indistinguishability Experiment Priv. K cpa A, (n) = (Gen, Enc, Dec), M , n Training Phase PPT Attacker A {0 b , 1} m 0, m 1 M, |m 0| = |m 1| Query: Plain-text I can break k c Enck(mb) Let me verify Gen(1 n) Response: Ciphertext Post-challenge Training Phase: >> A is given oracle access to Enck() >> A adaptively submits query (possibly including m 0, m 1) and receives their encryption

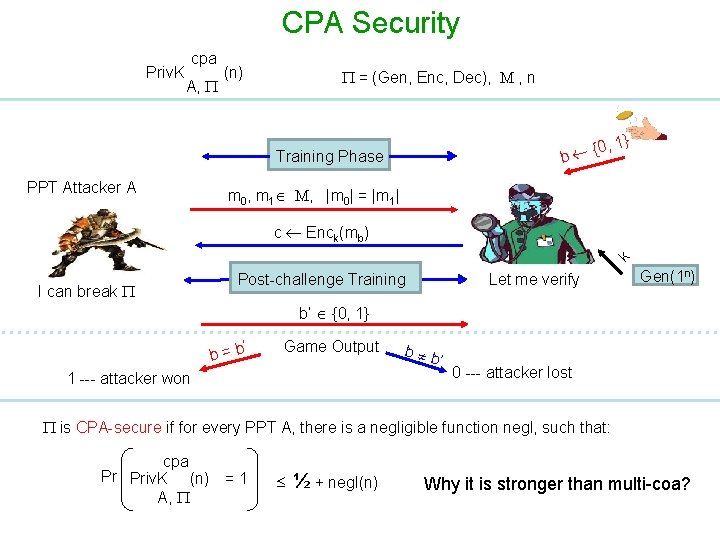
CPA Indistinguishability Experiment Priv. K cpa A, (n) = (Gen, Enc, Dec), M , n {0 b Training Phase PPT Attacker A , 1} m 0, m 1 M, |m 0| = |m 1| k c Enck(mb) I can break Post-challenge Training Let me verify b’ {0, 1} ’ b=b Game Output 1 --- attacker won b b ’ 0 --- attacker lost Response Phase: Ø A finally submits guess regarding encrypted challenge plain-text Ø A wins the experiment if its guess is correct Gen(1 n)

CPA Security Priv. K cpa A, (n) = (Gen, Enc, Dec), M , n {0 b Training Phase PPT Attacker A , 1} m 0, m 1 M, |m 0| = |m 1| k c Enck(mb) I can break Let me verify Post-challenge Training Gen(1 n) b’ {0, 1} ’ b=b Game Output 1 --- attacker won b b ’ 0 --- attacker lost is CPA-secure if for every PPT A, there is a negligible function negl, such that: cpa Pr Priv. K (n) = 1 A, ½ + negl(n) Why it is stronger than multi-coa?

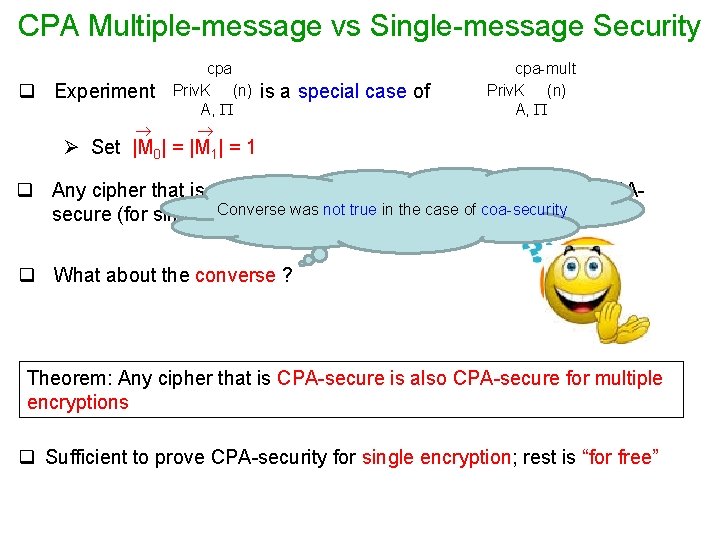
CPA Security for Multiple Encryptions cpa-mult Priv. K (n) A, = (Gen, Enc, Dec), M , n Training Phase PPT Attacker A M 0 = (m 0, 1, …, m 0, t) M 1 = (m 1, 1, …, m 1, t) {0 b , 1} (freedom to choose any pair) I can break Post-challenge Training k c 1 Enck(mb, 1) , …, ct Enck(mb, t) Let me verify Gen(1 n) b’ {0, 1} ’ b=b 1 --- attacker won Game Output b b ’ 0 --- attacker lost is CPA-secure for multiple encryptions if for every PPT A, there is a negligible function negl, such that: cpa-mult Pr Priv. K (n) = 1 ½ + negl(n) A,

CPA Multiple-message vs Single-message Security q Experiment cpa Priv. K (n) A, is a special case of cpa-mult Priv. K (n) A, Ø Set |M 0| = |M 1| = 1 q Any cipher that is CPA-secure for multiple encryptions is also CPAConverse was not true in the case of coa-security secure (for single encryption) q What about the converse ? Theorem: Any cipher that is CPA-secure is also CPA-secure for multiple encryptions q Sufficient to prove CPA-security for single encryption; rest is “for free”

CPA-security Guarantee in Practice q Ensures security against CPA even if multiple messages are encrypted using a single key and communicated >> Even if the adversary knows that the encrypted messages belong to one of the two possible “classes” >> Even if the adversary has seen encryptions of the messages in those classes in the past q Very good security guarantees >> The least we should expect from a SKE

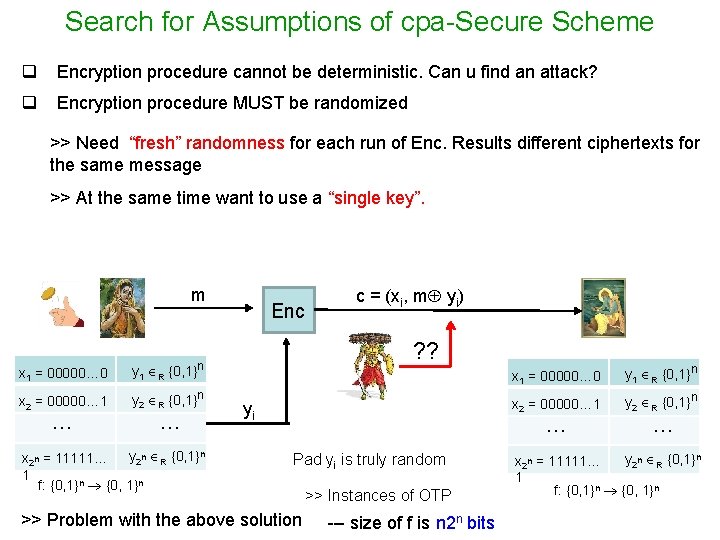
Search for Assumptions of cpa-Secure Scheme q Encryption procedure cannot be deterministic. Can u find an attack? q Encryption procedure MUST be randomized >> Need “fresh” randomness for each run of Enc. Results different ciphertexts for the same message >> At the same time want to use a “single key”. m x 1 = 00000… 0 y 1 R {0, 1}n x 2 = 00000… 1 y 2 R {0, 1}n … … y 2 n R {0, 1}n x 2 n = 11111… 1 f: {0, 1}n Enc c = (xi, m yi) ? ? yi x 1 = 00000… 0 y 1 R {0, 1}n x 2 = 00000… 1 y 2 R {0, 1}n … Pad yi is truly random >> Problem with the above solution >> Instances of OTP --- size of f is n 2 n bits … y 2 n R {0, 1}n x 2 n = 11111… 1 f: {0, 1}n

Assumptions for cpa-secure SKEs O. Goldreich, S. Goldwasser and S. Micali. How to Construct Random Functions. JACM, 33(4), 792 -807, 1986 Pseudorandom Functions (PRF) that “look” like TRF but actually not!!

Pseudorandomness - It’s a property of a probability distribution on a set Funcn = { Set of all functions f: {0, 1}n } Give me output for x U: Uniform probability Distribution G: a prob. Dist. = { Set of probabilities } We are interested in A function drawn according certain type of G. Sampler for G and U to U is called truly random function (TRF) y G is pseudorandom if a function drawn according to G is indistinguishable from a function drawn according to U to a PPT distinguisher who can make PPT no. of queries

Funcn & Uniform Distribution & TRF Funcn = { Set of all functions f: {0, 1}n } |Funcn| = n 2 n. 2 x 1 = 00000… 0 2 n possibilities x 2 = 00000… 1 2 n possibilities … 2 n possibilities x 2 n = 11111… 1 2 n possibilities = {f 1, f 2, …, f n 2 n. 2 U = {1/2 n. 2 n } , 1/2 n. 2 n , …, 1/ n. 2 n 2 n 2 n q Truly Random Function (TRF): chosen according to U >> Output behavior is completely unpredictable >> Every string of length n is a possible image with equal probability }

Pseudorandom Functions (PRF) > PRF- A function chosen from Funcn according to some distribution different from U - yet, its output behavior “looks like” a TRF - must be efficiently computable - Function specification must be concise (poly size) o Definitely not by truth table which will be of size n 2 n o The sender & the receiver needs to agree on the function > keyed functions fk (. ): {0, 1}n Funcn : { Set of all functions f: {0, 1}n } n |Funcn| = 2 n. 2 TRF: A function chosen uniformly at random from Fn KFuncn : { Set of all KEYED functions fk: {0, 1}n } Funcn |KFuncn| = 2 n PRF: A function chosen uniformly at random from KFuncn and “behaves” like a TRF

A possible Definition of PRF in PRG style q Give F (table) either uniformly sampled from Funcn or from KFuncn to PPT distinguisher D and ask if it is a TRF or PRF. >> Does it work? >> No, since the description of the function is of exponential size >> Instead we give D oracle access to either a TRF or a PRF and ask “tell us who are you interacting with? ” >> If D cannot tell apart the “behavior” of the function Fk (for a uniformly random k) from a truly random function f: {0, 1}n, then we say f is a PRF.

Indistinguishability Game for PRF F: {0, 1}n x {0, 1}n Funcn = {f 1, f 2, …, f Oracle }n 2 n. 2 x 1 Value of the function at x 1 b= 0 PPT distinguisher D KFuncn = {Fk , …, Fkn } 1 2 Value of the function at x 1 is y 1 b y 1 = ) 1 x ( f f R Funcn

Indistinguishability Game for PRF F: {0, 1}n x {0, 1}n Funcn = {f 1, f 2, …, f Oracle }n 2 n. 2 xt Value of the function at xt b= 0 PPT distinguisher D KFuncn = {Fk , …, Fk n } 1 Value of the function at xt is yt 2 • D can adaptively asks its queries • D allowed to ask polynomial number of queries b yt ) (x t f = f R Funcn

Indistinguishability Game for PRF F: {0, 1}n x {0, 1}n Funcn = {f 1, f 2, …, f } n 2 n. 2 Value of the function at x 1 PPT distinguisher D KFuncn = {Fk , …, Fk n } 1 2 Value of the function at x 1 is y 1 b= 1 k R b x 1 y 1 = {0, 1} n F( k x 1 ) Fk

Indistinguishability Game for PRF F: {0, 1}n x {0, 1}n Funcn = {f 1, f 2, …, f } n 2 n. 2 Value of the function at xt PPT distinguisher D KFuncn= {Fk , …, Fk n } 1 Value of the function at xt is yt 2 b= 1 k R b xt yt = {0, 1} n F( k xt ) Fk • D can adaptively asks its queries • D allowed to ask polynomial number of queries

Modeling PRF as an Indistinguishability Game Funcn = {f 1, f 2, …, f }n 2 n. 2 F: {0, 1}n x {0, 1}n ? ? PPT distinguisher D (x 1, y 1), (x 2, y 2), …, (xk, yk) KFuncn= {Fk 1, …, Fk 2 n } F is a PRF if for every PPT D there is an negl(n) | Pr [D Fk( ) (1 n) = 1] - Pr [D f( ) (1 n) = 1] >> uniformly random k >> uniform choice of f >> D‘s randomness >> D’s randomness | negl(n) >> D not given k in the above game --- otherwise D can distinguish with high probability

Let’s Try to Construct a PRF Consider the following keyed function F Input: x Output: k x length-preserving For any x, uniformly random output (if k is uniformly random) F is noaway PRFa PRF Oracle xi Value of of the function at at xx 12 PPT distinguisher D (x 1, y 1), (x 2, y 2) y 2 y 1 x 2= x 1 x 2 1 q | b= 0 y 2 R b= 1 xi yi = 0 F( k If D interacted with a random keyed Fkfunctionf( ) Fk( ) = Pr [D (1 n) = 1] Ø D outputs 1 only with probability if f(x 2) = f(x 11) x 1 x 2 --- prob: 2 -n - f R Funcn k Value of of the function at at xx 12 is is yy 12 y 1 yi ) (x i f = | 1 – 2 -n {0, 1} n xi ) Fk

Do PRFs exist? No proof… But we strongly believe they do Didn’t we just say we believe something is true but don’t have a proof? Yet another Assumption: PRFs exist. Later in the course………. PRFs exist li CT 7 (for 1) ica r-M e s ? ? as -G dw ol d ol ich re G PRGs exist Far from practical Be ca us en og oo dd ist ing uis he r Block Ciphers: DES, AES Highly practical

Pseudo Random Permutation (PRP) Permn = {f 1, f 2, …, f } (2 n)! F: {0, 1}n x {0, 1}n ? ? PPT distinguisher D (x 1, y 1), (x 2, y 2), …, (xk, yk) KPermn = {Fk 1, …, Fk n } Distinct pairs 2 F is a PRF if for every PPT D there is an negl(n) | Pr [D Fk( ) (1 n) = 1] - Pr [D f( ) (1 n) = 1] >> uniformly random k >> uniform choice of f >> D‘s randomness >> D’s randomness | negl(n)

TRF & TRP RA: No PPT distinguisher can tell apart between TRF & TRP. (use Birthday paradox KL A. 4. )

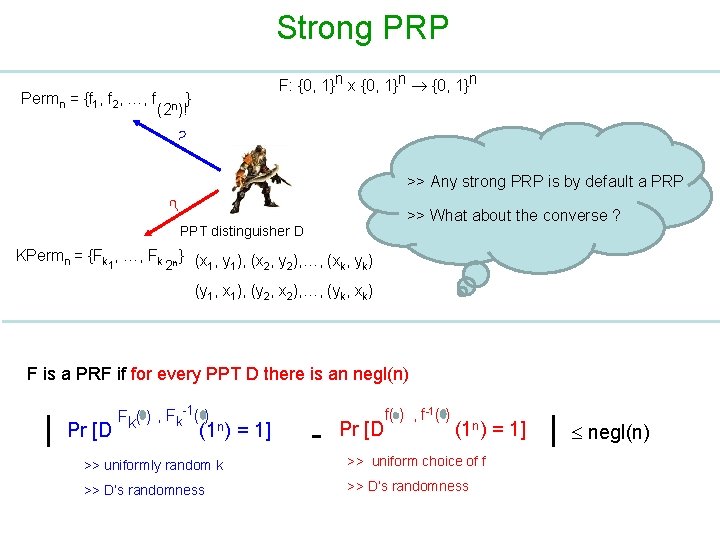
Strong PRP Permn = {f 1, f 2, …, f F: {0, 1}n x {0, 1}n } (2 n)! ? >> Any strong PRP is by default a PRP ? >> What about the converse ? PPT distinguisher D KPermn = {Fk 1, …, Fk 2 n } (x , y ), …, (x , y ) 1 1 2 2 k k (y 1, x 1), (y 2, x 2), …, (yk, xk) F is a PRF if for every PPT D there is an negl(n) | Pr [D Fk( ) , Fk-1( ) (1 n) = 1] - Pr [D f( ) , f-1( ) (1 n) = 1] >> uniformly random k >> uniform choice of f >> D‘s randomness >> D’s randomness | negl(n)

Do PRPs/SPRPs exist? No proof… But we strongly believe they do Yet another Assumption: PRPs/SPRPs exist. Later in the course………. PRPs/SPRPs exist f f ko by u L ac R - Be ca us en og oo dd ist ing uis he PRFs exist Far from practical r Block Ciphers: DES, AES Highly practical Efficiency of SPRPs based cpa-secure schemes are better than PRF-based ones