Lesson 8 Objectives Recap and iteration practice Reduction

Lesson 8 Objectives • • • Recap and iteration practice Reduction of B. E. to 1 D 1 D Quadratures 8 -1

Recap of where we are 1. The forward Boltzmann equation in space, energy, angle equation was derived to be: • The left side held the flux-dependent terms, the right side held the non-flux-dependent term. We also derived the adjoint form of the equation (which we will ignore the rest of the course) • 8 -2

Recap of where we are (2) 2. In the absence of an external source, we found that we had to add an eigenvalue to the equation. We learned four variations on this, the most common being the k-effective (or lambda) eigenvalue: • The fission neutron source term became our new “source”, so we moved it to the right hand side. 8 -3

Recap of where we are (3) 3. We then began attacking the equation, beginning with energy. We approximated the energy dependence of the flux and cross sections using the MULTIGROUP equation with (after proper approximation of the group parameters), gave us (for each group): • This “theme” of throwing more and more over to the “source” term will continue as we go! 8 -4

Recap of where we are (4) 4. Since the only non-g term of the left hand side was the scattering from other groups, we then (what else) relegated all of the non-g scattering to the right-hand-side to get: • We label the new source “out” because it becomes the source for each group in an OUTER iteration, where each of the energy groups are treated one-at-a-time. • We learned two ways of computing the source, depending on whether the inscattering sources from groups that have already been handled in the current outer iteration use the OLD iteration fluxes (“Jacobi”) or the NEW iteration fluxes (“Gauss-Seidel”) 8 -5

Recap of where we are (5) • Adding in the outer iteration “counters”, , makes this: • The “? ” is there because the iteration counter depends on whether you are using Jacobi or Gauss-Seidel (and, if G-S, whether g’ is a group that has already been calculated in the current outer iteration) I gave you some practice using this in HW#7 • 8 -6

Recap of where we are (6) 5. Just for a little practice in the numerical treatment of outer iterations, we reduced this to the infinite-medium-form, where the flux does not depend on either space or direction, giving us: • Following the traditional notation, this equation was written in terms of the SCALAR flux (the direction-integrated ANGULAR flux) because, for isotropic infinite-medium fluxes, they are the same value (as long as you use unit solid angle): 8 -7

Recap of where we are (7) Whenever you use an iterative method, if the numerical method is convergent, the fluxes will change less and less with each iteration. The user has to decide when close enough is good enough. Usually this is done with a convergence criterion of the MAXIMUM FRACTIONAL CHANGE of any iterating variable. • • After each iteration, you loop over each flux value and determine the fractional amount it has changed during this iteration. You find the maximum ABSOLUTE VALUE of any change and that becomes your “error” value for the iteration. You continue iterating until either: 1. 2. • The absolute value of your iteration error is less than some preset CONVERGENCE CRITERION; or You have exceeded the maximum number of iterations you will allow (necessary so that a divergent problem doesn’t run forever) In setting the convergence criterion, you must be careful not to demand more digits than the computer uses for a variable! (This is why FRACTIONAL change is used. ) I like 1. 0 e-06 8 -8

Recap of where we are (8) 6. Concentrating our attention on the solution within each group (dropping the outer iteration counter since they are all ): we again simplified by throwing the more complicated withingroup scattering term to the right-hand-side to get: • Using an INNER iteration counter of k, this becomes: 8 -9

Recap of where we are (9) 7. Just for a little practice in the numerical treatment of outer iterations and inner iterations at the same time, we reduced this to the infinite-medium-form, where the flux does not depend on either space or direction, giving us: • Notice that I did NOT use the removal cross section YOU MUST BE SURE to start each inner iteration with the initial fluxes set to the BEST AVAILABLE fluxes for that group (i. e. , the results of the last time this group was calculated). DO NOT reset them to zero; they are only set to 0 the first time. • 8 -10

Recap of where we are (10) Whenever you are dealing with BOTH inner and outer iterations, you have to decide how finely to converge the inner iterations before moving on to the next group. Basically, this comes down to setting the maximum number of inner iterations to run for each outer sweep through a group. The two limiting cases of this parameter are 1 and infinity, i. e. , 8. • • • Running just one inner iteration per outer iteration; and Converging the inner iterations FULLY before moving on, no matter how long it takes. Although this decision is problem dependent, usually a good value can be found. (At SRP, we used 4. ) FYI, it is frequently done that the INNER iteration convergence criterion is smaller than the OUTER iteration convergence criterion (I like to use half). This helps keep the number of outer iterations lower. 8 -11

Treatment of Space and Direction • Now we move on to solve the group equations in both direction and space • You might THINK that we would treat one of them first and then move on to the next one. BUT, since multidimensional problems are more difficult than one-dimensional problems, we shall instead attack: • Both space and direction in one-dimensional problems and THEN • Both space and direction in multi-dimensional problems So, next is the treatment of one dimensional problems. We shall also break THIS up by difficulty, looking at: • • • One dimensional SLAB geometries; and then One dimensional CURVED geometries (cylindrical and spherical). 8 -12

Reduction to 1 D Slab • To concentrate our attention on our angular treatments, we will simplify space to 1 D slab geometry: • where the second relation reminds that the angular dependence of the source is given as Legendre source moments. 8 -13

Quadrature integration • • • In a minute, we are going to represent the angular dependence of the angular flux as a quadrature. But, since this is a relatively obscure mathematical practice, let’s review what a quadrature is and the specific properties of a Gauss-Legendre quadrature. Whereas an expansion is used to approximate a function at all points of the domain: a quadrature is used to approximate the integral of a function between a and b by sampling specific points of the function and using a weighted sum (with weights summing to 1): 8 -14

Quadrature integration (2) • The different quadratures differ in the number of points sampled, the prescription of the values to be sampled, and how much weight each is given: • The most common quadratures use equally spaced x values, but use specially chosen weights: • • Reimann sum: N cell-centered x’s, weights=1/N Trapezoidal rule: N+1 cell-edged x’s, weights=(0. 5, 1, 1, …, 1, 0. 5)/N Simpson’s rule: N+1 cell-edged x’s, weights=(1, 4, 2, …, 2, 4, 1)/(3 N) Example: • • • Reimann: 2(0. 5^3+1. 5^3)=3. 5 Trapezoidal: 2(0. 5*0+1*1+0. 5*8)=5 Simpson’s: 2(1*0+4*1+1*8)/3)=4 (Simpson’s rule is exact up to 3 rd order) 8 -15

Gauss-Legendre Quadrature • • An Nth-order Gauss-Legendre quadrature is RESTRICTED to integrals between -1 and 1 (although they can be adapted for other domains). This quadrature defines the wn’s and the xn’s by the following rules: • The xn’s are chosen to be the roots of the Nth order Legendre polynomial: • The wn’s are chosen so that the Legendre moments up to order 2 N-1 are satisfied exactly, i. e. , with weights summing to 1: 8 -16

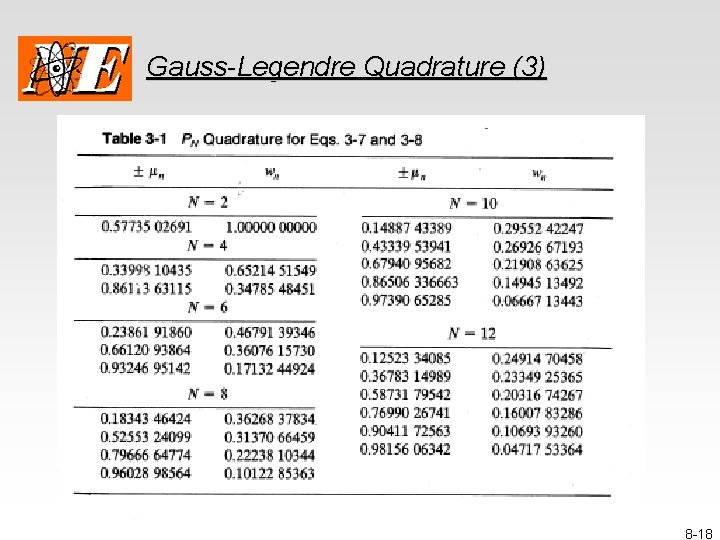
Gauss-Legendre Quadrature (2) The power of a Gauss-Legendre quadrature is that an Nth-order Gauss-Legendre quadrature integrates a (2 N-1)th order polynomial exactly. The resulting quadrature sets are given in text on Table 3 -1. • • NOTE: Only the positive values of the xn are given. You must include the negative values as well (with the same weights. ) NOTE: The ORNL code convention is to have all weights add up to 1. The text follows the convention that the weights add up to the width of the domain of integration (i. e. , 2 for our problems). In effect, they incorporate the (b-a) term into the weights. 8 -17

Gauss-Legendre Quadrature (3) 8 -18

Application of SN quadrature to direction • • We will now apply the Gaussian quadrature to our direction variable. Why? Because, we nuclear engineers are seldom interested in the angular flux itself. We are much more interested in REACTION RATES, which are determined from the scalar flux, which in slab geometry is: 8 -19

Applic. of SN quadrature to direct’n (2) • This approach also fits well with our definition of the angular source, for which we use flux moments: 8 -20

Resulting equation • The final result is that we calculate the angular flux ONLY IN PARTICULAR DIRECTIONS (“discrete ordinates”): • We will begin the spatial attack next week 8 -21

Homework 8 -1 • Using the information on slide 8 -16, find the Legendre weights and values for N=4 and N=6. (And check them against the Table 3 -1 values on slide 8 -18. ) You may find the following recurrence relation to be of use: 8 -22

Homework 8 -2 • Solve for a. : b. • using the Legendre-based quadratures from Table 3 -1 of the text. For each of them, use the 2, 4, 6, 8, 10, and 12 order quadrature parameters. Solve for by using proportional x values (same weights) 8 -23

Homework 8 -3 • Demonstrate (not prove) that use of the N=12 quadrature can exactly integrate powers of xl between -1 and 1 for up to l=2 N-1=23. between. • Since roundoff error is unavoidable, it is sufficient to show me results for l=0 to (say) 30 and show that very low errors become notso-low errors after 23. 8 -24