Differentiation recap Rules you must remember Rules on

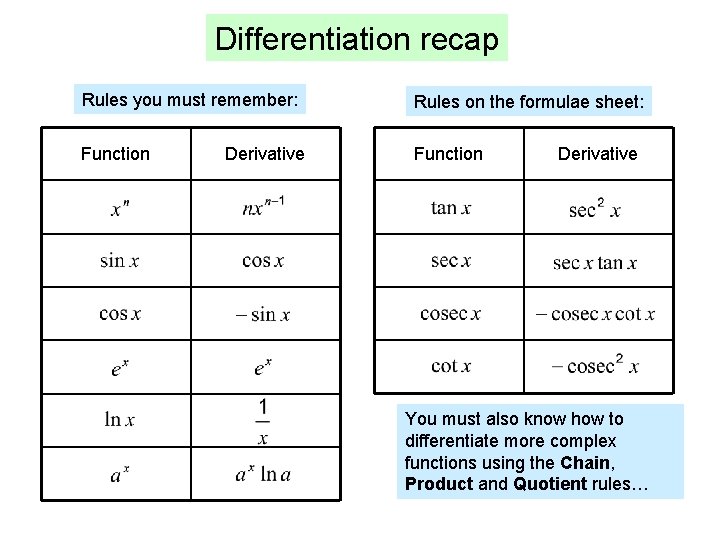
Differentiation recap Rules you must remember: Rules on the formulae sheet: Function Derivative You must also know how to differentiate more complex functions using the Chain, Product and Quotient rules…

Differentiation recap You have already met the following rules: The Chain Rule: If Eg then or Eg If then Eg The Product Rule: If then Eg The Quotient Rule: If then Eg

Maclaurin Taylor Series • KUS objectives BAT Starter:

Notes 1 • A wide range of functions of x can be expressed as an infinite series (a bit like the Binomial Expansion) • These are sometimes called a ‘power series’ • These are used very often as they can allow us to find values of things such as Sinx or Cosx to whatever degree of accuracy we want • Remember that many values of Sin and Cos are irrational numbers, hence cannot always be calculated exactly • The series sum idea is possibly what your calculator does to calculate values such as Sin 20 etc…

Notes 1 NOTATION Differential 2 nd Differential 3 rd Differential 4 th Differential 1 st nth Differential You need to understand this next piece of notation this means find the value of the 4 th differential when x = 6

Differentiate using the rule for ln Differentiate using the chain rule (rewrite as a bracket to a power first)

Differentiate using the rule for ‘e’ Differentiate using the product rule Simplify by grouping like terms

WB 3 Complete the table:

Practice Ex 205 A

KUS objectives self-assess One thing learned is – One thing to improve is –

END