Section 7 2 Inverse Transforms and Transforms of






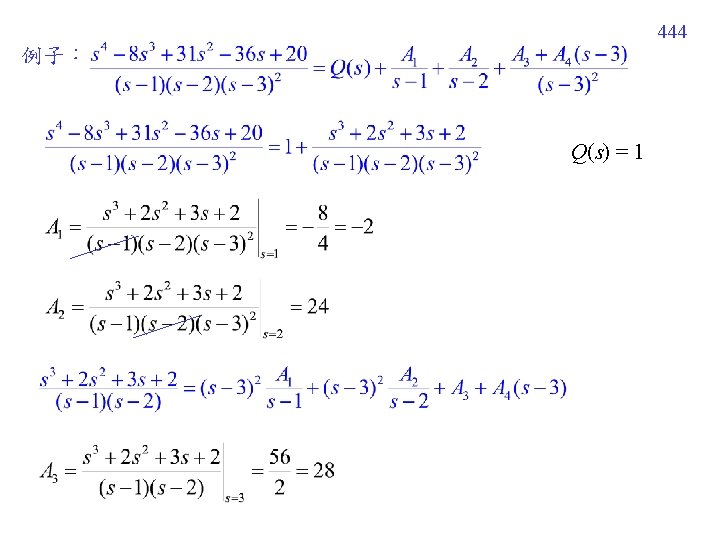
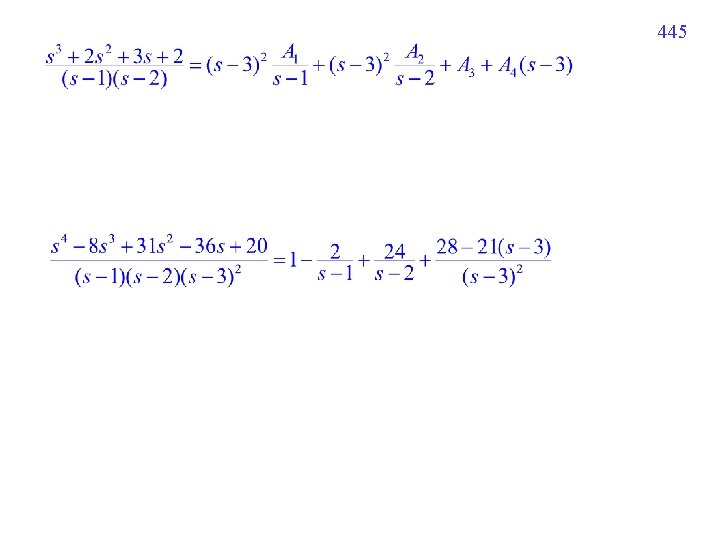

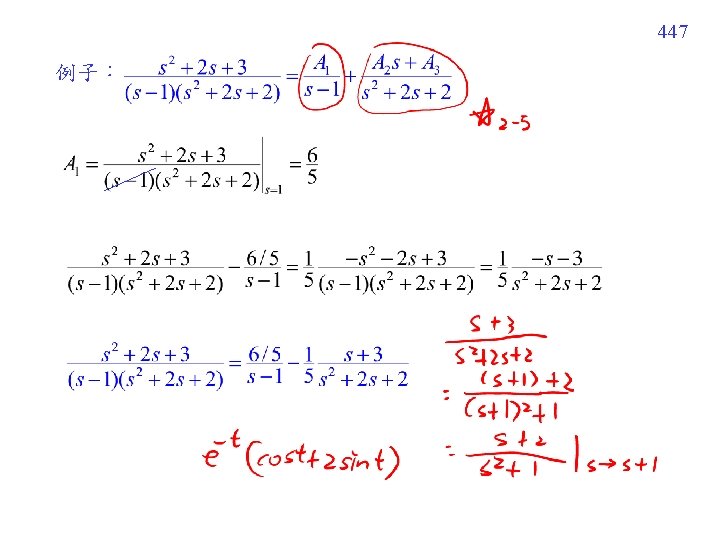



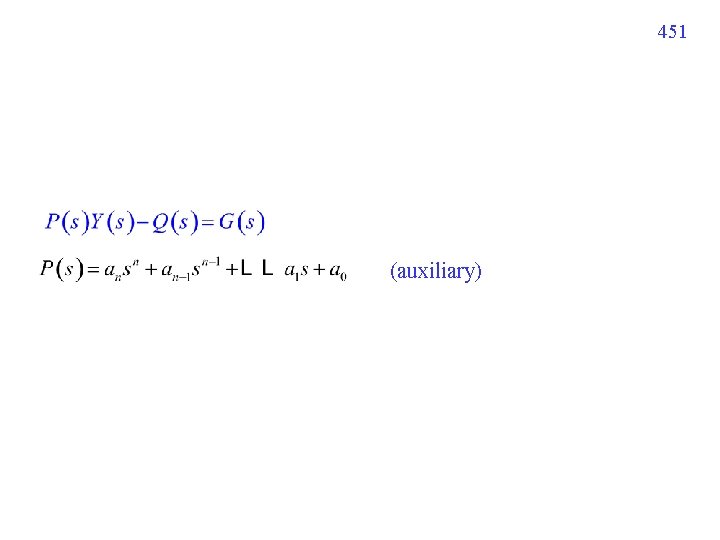




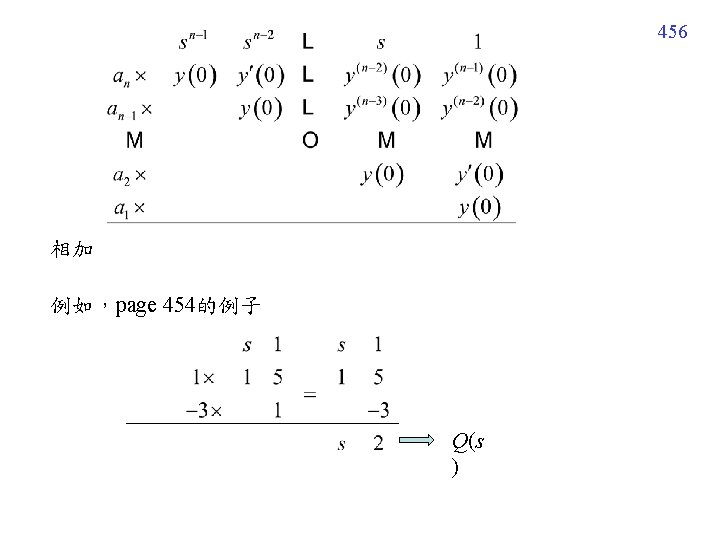







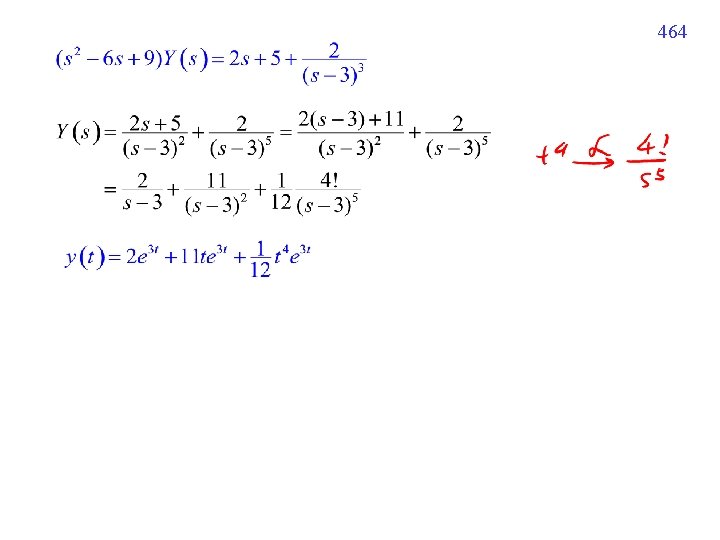

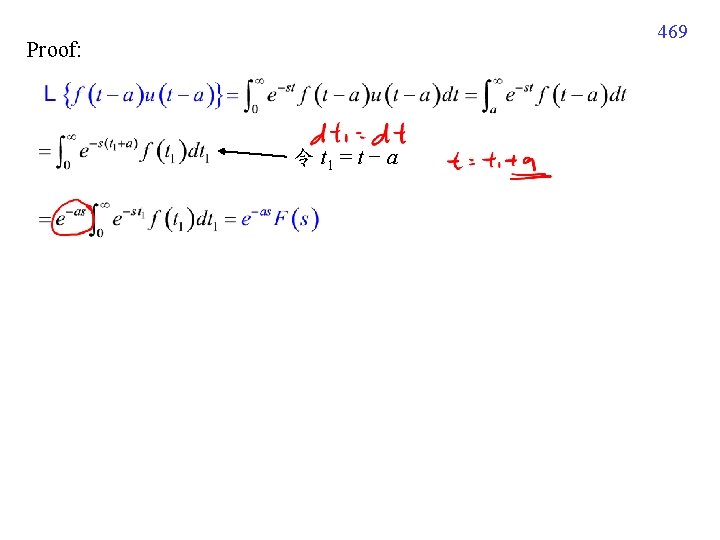













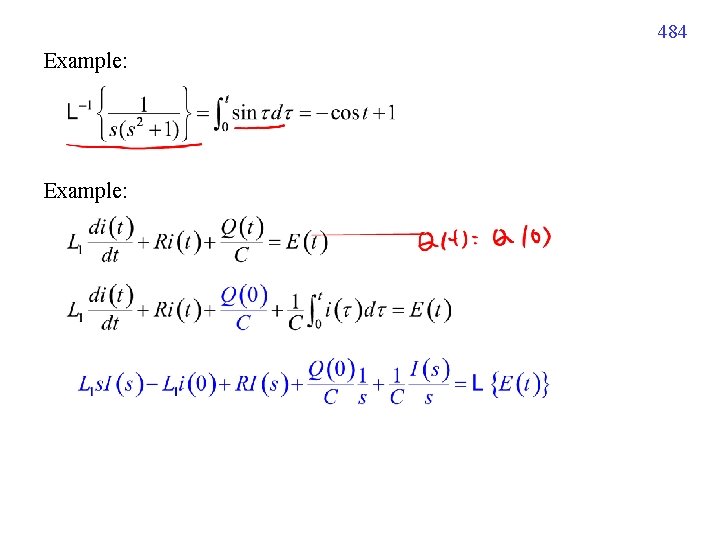

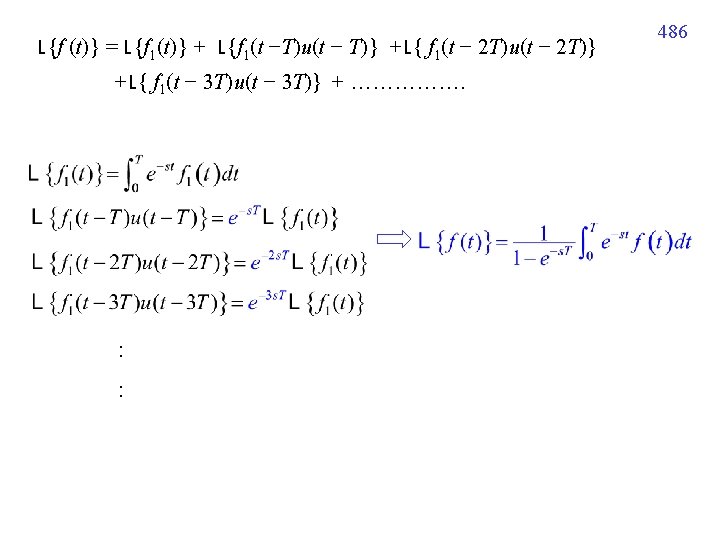
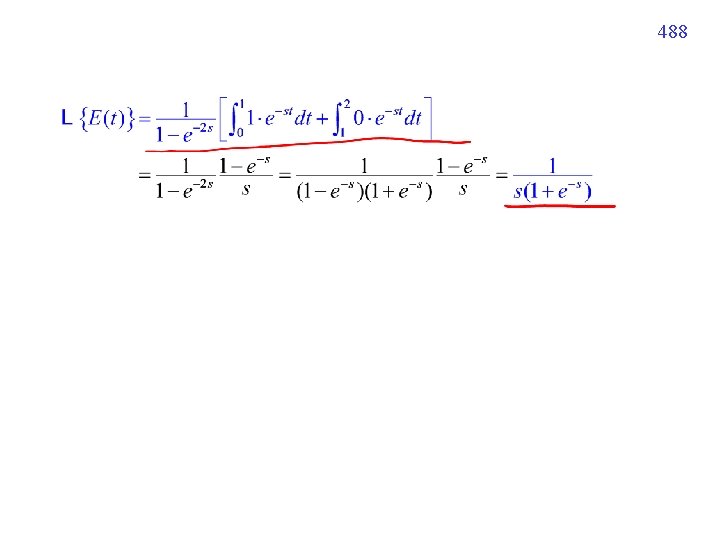

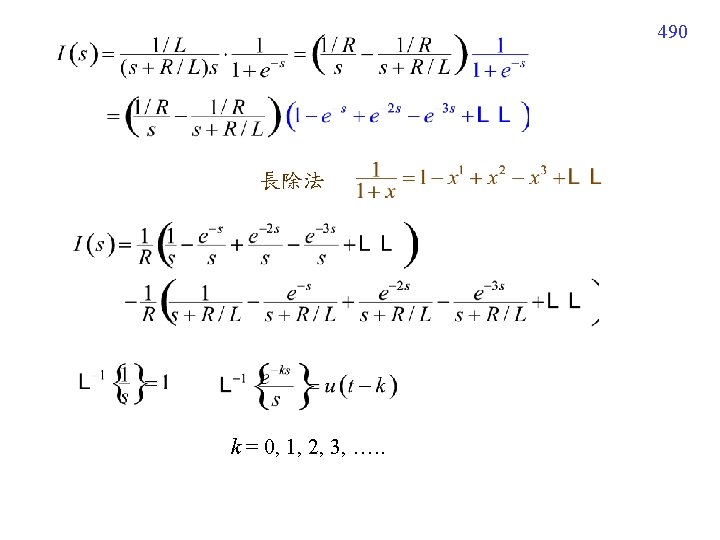












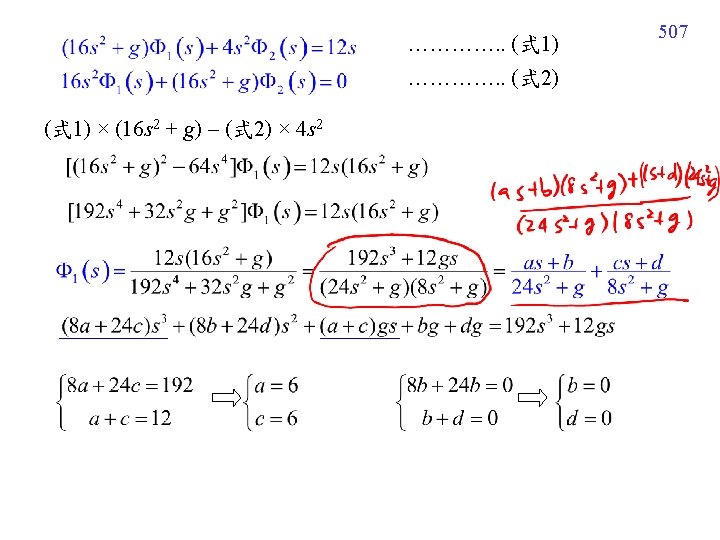

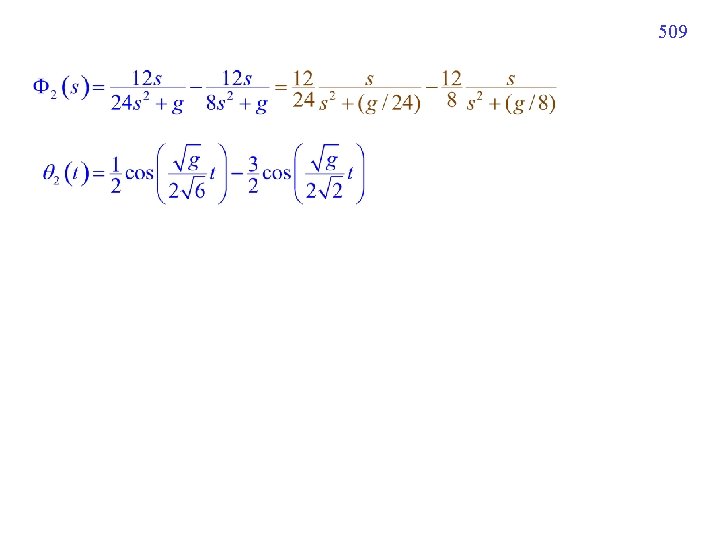











- Slides: 84

Section 7 -2 Inverse Transforms and Transforms of Derivatives 本節有兩大部分: (1) inverse Laplace transform 的計算 (7 -2 -1 ~ 7 -2 -3) (2) 將微分變成 Laplace transform 當中的乘法 (7 -2 -4 ~ 7 -2 -6) 437

438 7 -2 -1 Inverse 方法一: One-to-One Relation When (1) f 1(t) and f 2(t) are piecewise continuous on [0, ), and (2) f 1(t) and f 2(t) are of exponential order, then if f 1(t) f 2(t) then F 1(s) F 2(s) 換句話說,在這種情形下,Laplace transform 是 one-to-one 的運算。 If the Laplace transform of f 1(t) is F 1(s), then the inverse Laplace transform of F 1(s) must be f 1(t).

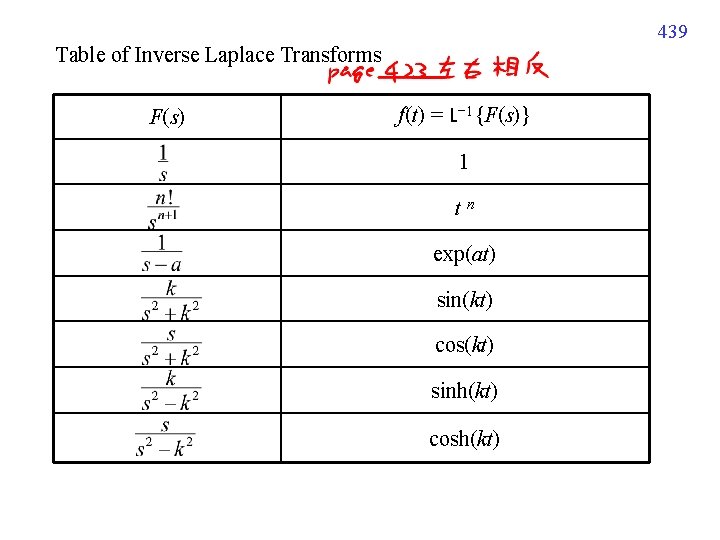
439 Table of Inverse Laplace Transforms F(s) f(t) = L− 1{F(s)} 1 tn exp(at) sin(kt) cos(kt) sinh(kt) cosh(kt)

440 Example 1 (text page 287) (a) Example 2 (text page 287)

441 7 -2 -2 Inverse 方法 (二) Decomposition of Fractions Example 3 (text page 288) 問題:A, B, C 該如何算出? 太麻煩


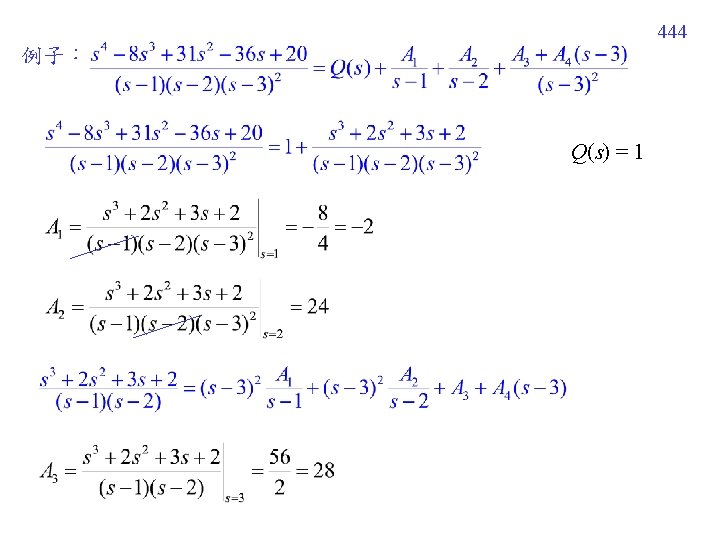
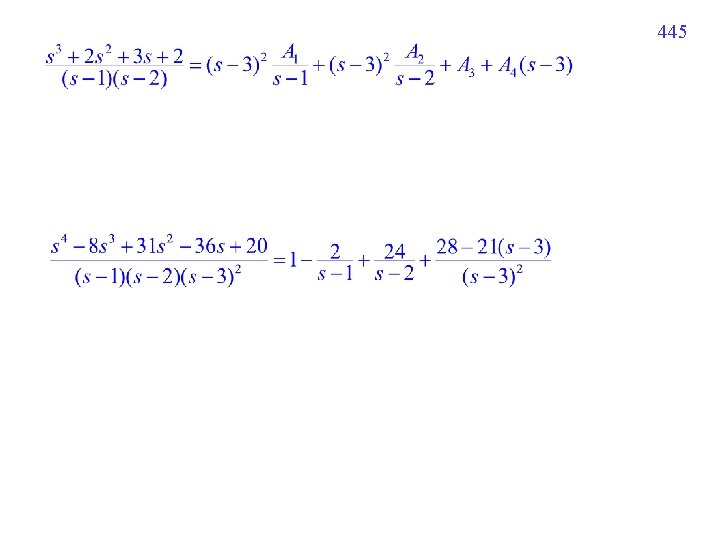
445

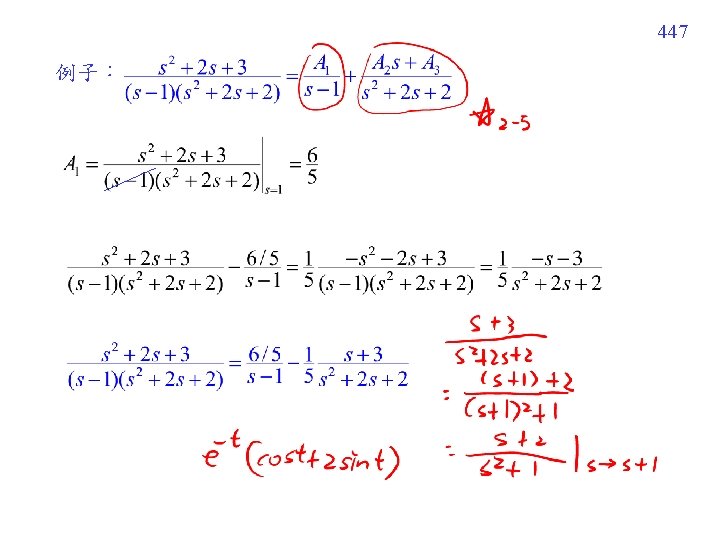

448 7 -2 -4 Transforms of Derivatives

449 Theorem 7. 2. 2 Derivative Property of the Laplace Transform

450 7 -2 -5 Solving the Constant Coefficient Linear DE by Laplace Transforms Laplace transform
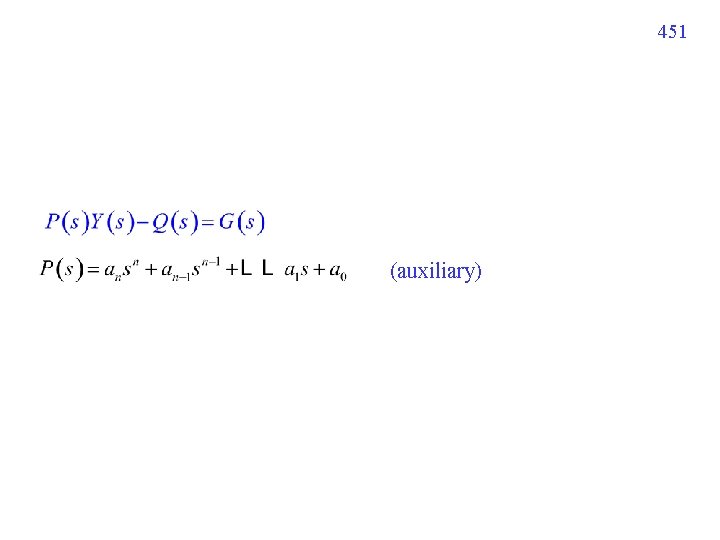
451 (auxiliary)

452 G(s): Laplace transform of the input Q(s): caused by initial conditions Y(s): Laplace transform of the response W(s): transform function L− 1[W(s)Q(s)]: zero-input response or state response L− 1[W(s)G(s)]: zero-state response or input response

Example 4 (text page 290) (Step 1) Laplace Transform (Step 2) Decompose (Step 3) Inverse Laplace Transform 453

Example 5 (text page 291) (Step 1) Laplace (Step 2) Decompose (Step 3) Inverse 快速法 454

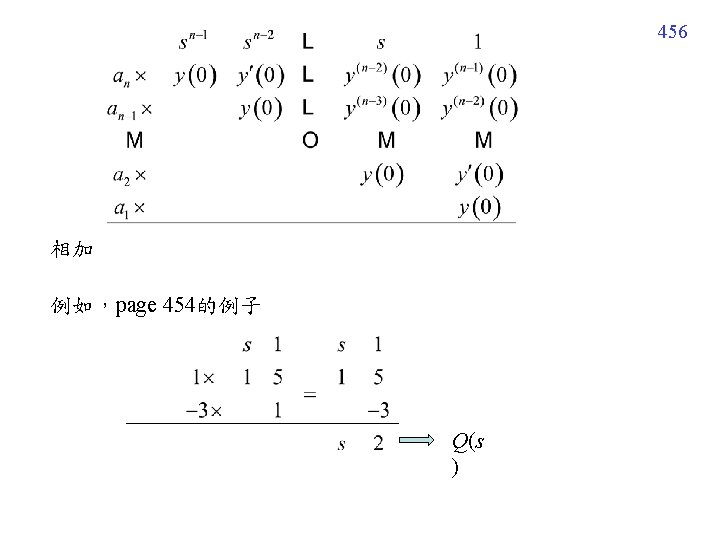


Section 7 -3 Operational Properties I 介紹兩個可以簡化 Laplace transform 計算的重要性質 First Translation Theorem (translation for s) Second Translation Theorem (translation for t) u(t): unit step function (注意兩者之間的異同) 458

7 -3 -1 First Translation Theorem (Translation for s) Proof: 459

7 -3 -1 -1 Inverse of “Translation for s” When f(t) is piecewise continuous and of exponential order (一對一) 註: Sections 7 -3 和 7 -4 其他的定理亦如此 460

7 -3 -1 -2 Examples Example 1 (text page 295) (a) (b) 461

462 Example 2 (text page 296) (a) (b)

463 Example 3 (text page 297) s 1 Q(s) = +
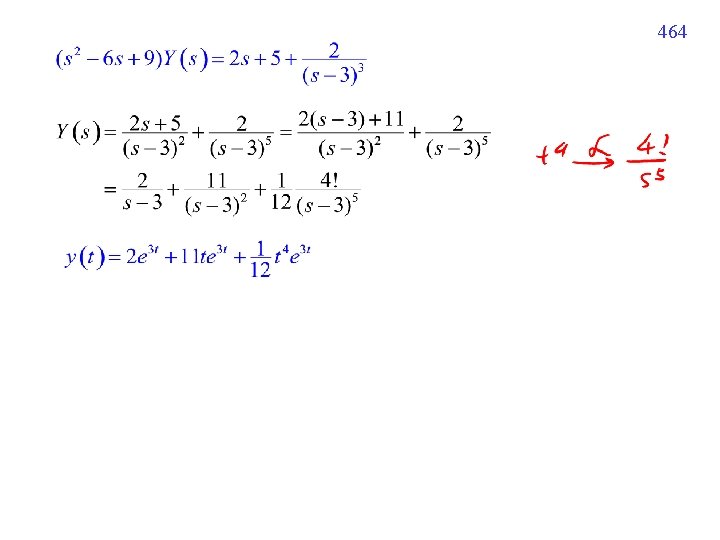
464

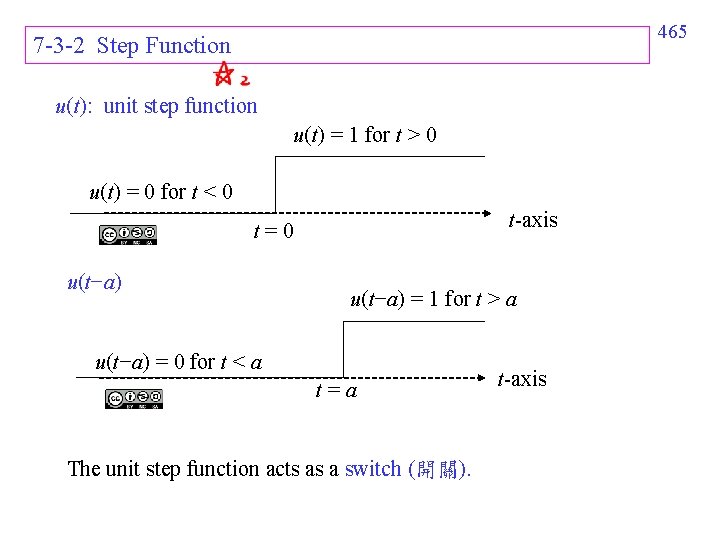
465 7 -3 -2 Step Function u(t): unit step function u(t) = 1 for t > 0 u(t) = 0 for t < 0 t-axis t=0 u(t−a) = 1 for t > a u(t−a) = 0 for t < a t=a The unit step function acts as a switch (開關). t-axis

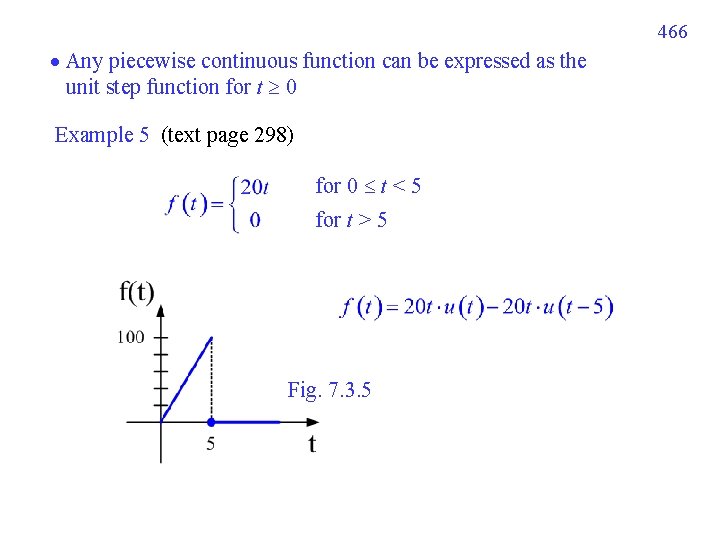
466 Any piecewise continuous function can be expressed as the unit step function for t 0 Example 5 (text page 298) for 0 t < 5 for t > 5 Fig. 7. 3. 5

467 In general, for 0 t < a for t > a

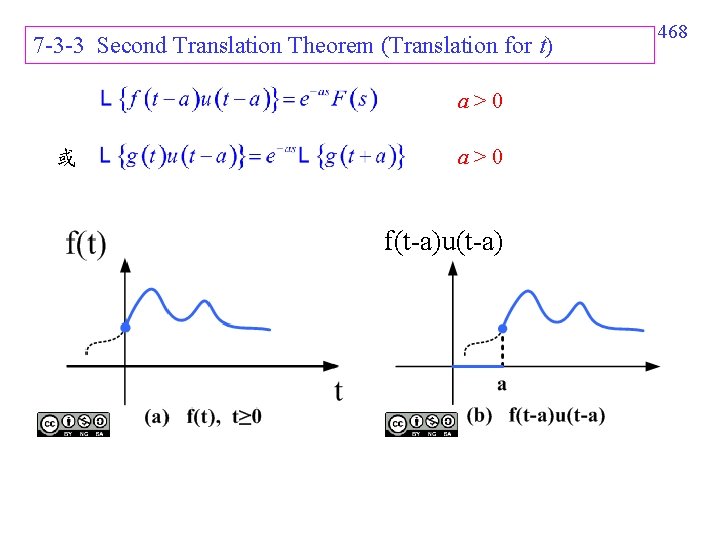
7 -3 -3 Second Translation Theorem (Translation for t) a>0 或 a>0 f(t-a)u(t-a) 468
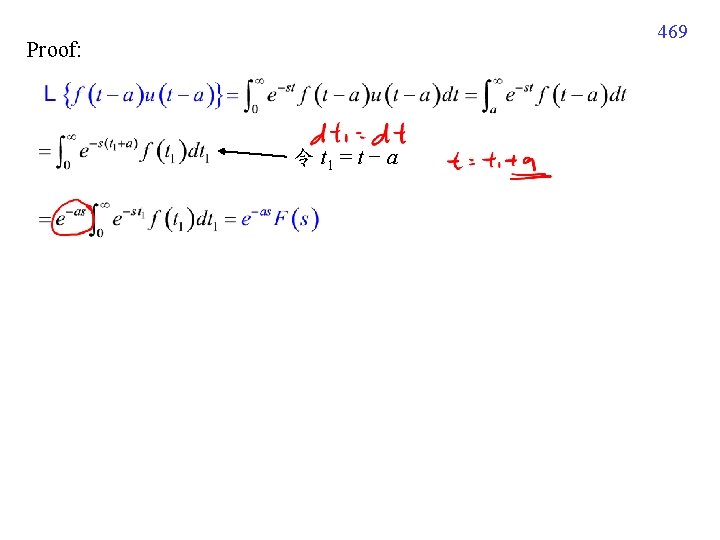
469 Proof: 令 t 1 = t − a

470 Example 7(a) (text page 300) Example 8 (text page 300)

Example 9 (text page 301) 471 for 0 t < for t

472

7 -3 -4 本節需要注意的地方 (1) 套用 “translation for t” 的公式時, 先將 input 變成 g( t + a ) 再作 Laplace transform (例如 Example 7) (2) Second translation theorem (translation for t) 當 a > 0 時才適用 (3) 套用公式時,注意「順序」 473

Section 7 -4 Operational Properties II 7 -4 -1 Derivatives of Transforms 比較: 微分 Laplace 乘 tn Laplace 乘 sn 微分 474

Proof of the Theorem of Derivatives of Transforms: 475

476 Example 1 (text page 307) 練習:為何

477 7 -4 -2 Convolution (旋積) Definition of convolution: (標準定義) * 代表 convolution (課本關於 convolution 的定義) When f(t) = 0 for t < 0 and g(t) = 0 for t < 0 , 上方的式子可以簡化為下方的式子



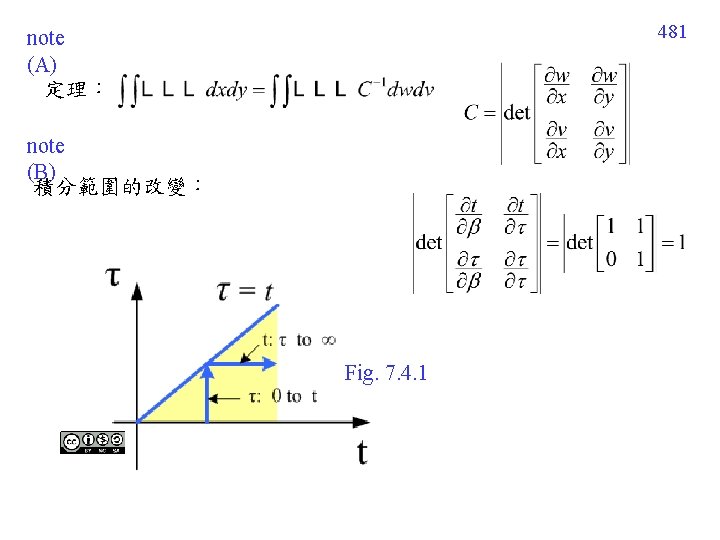
480 7 -4 -3 Convolution Theorem Convolution Multiplication Proof: note (A) 令 t = + 見後頁說明 note (B ) 見後頁說明


Example 3 (text page 308) Compute Example 4 (text page 309) Example 5 (text page 309) 482

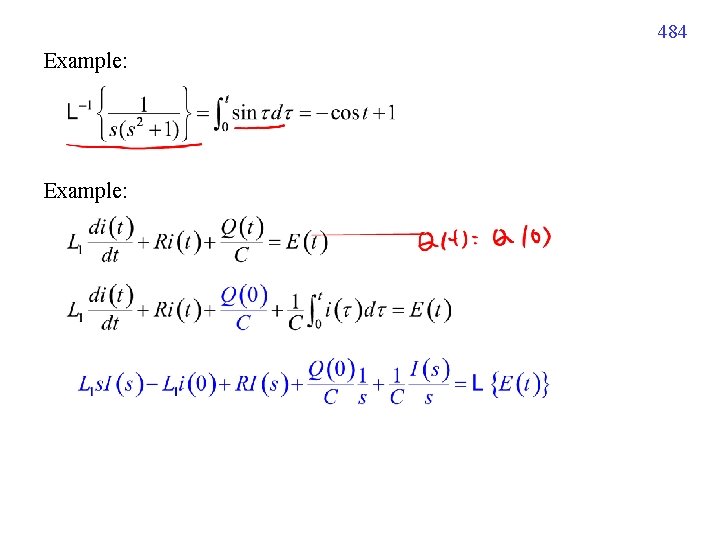
484 Example:

7 -4 -5 Transform of a Periodic Function 485 Theorem 7. 4. 3 When f(t + T) = f(t) then Proof: 令 f 1(t) = f (t) f 1(t) = 0 when 0 t < T otherwise f (t) = f 1(t) + f 1(t − T) + f 1(t − 2 T) + f 1(t − 3 T) + ……………. = f 1(t) + f 1(t −T)u(t − T) + f 1(t − 2 T) u(t − 2 T ) + f 1(t − 3 T) u(t − 3 T ) + …………….
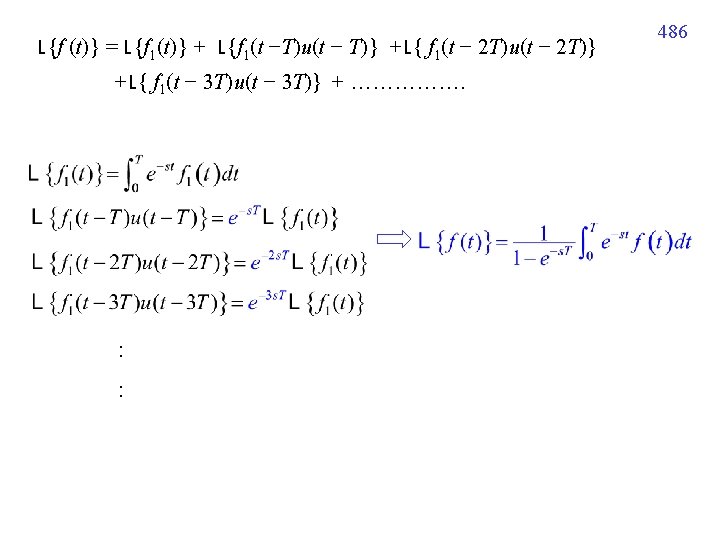

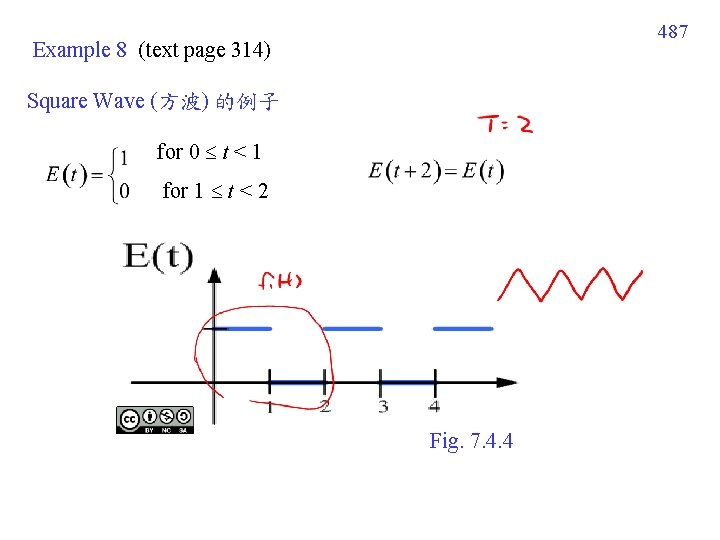
487 Example 8 (text page 314) Square Wave (方波) 的例子 for 0 t < 1 for 1 t < 2 Fig. 7. 4. 4
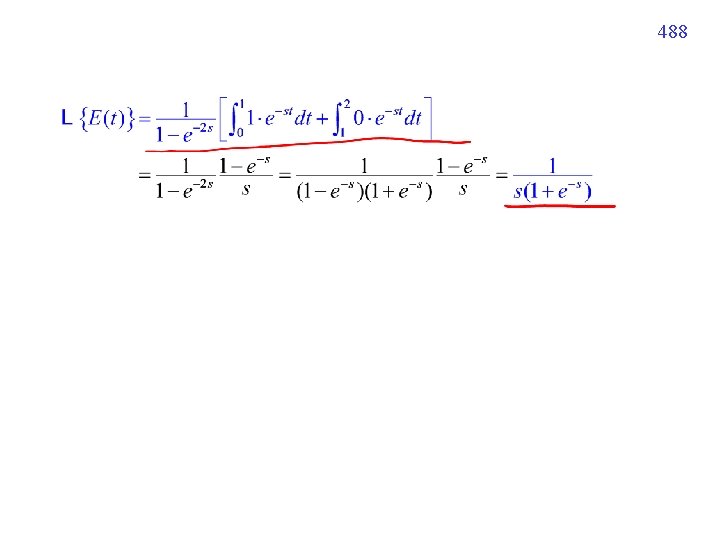
488

489 Example 9 (text page 314) E(t) 為 page 487 之方波
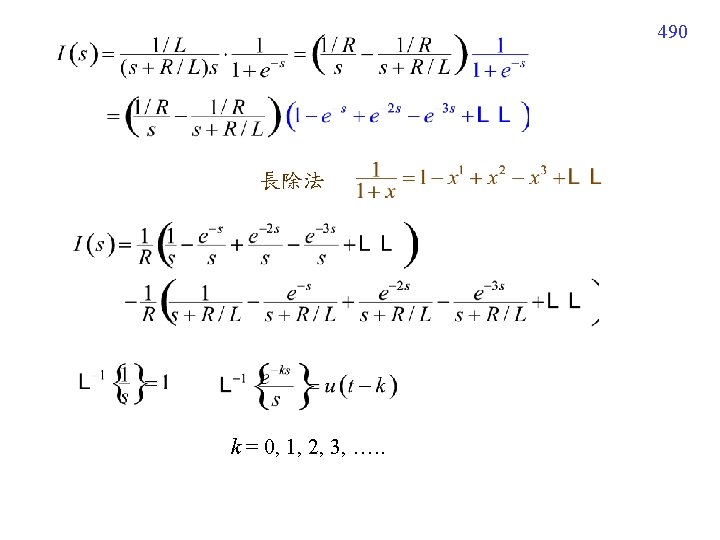



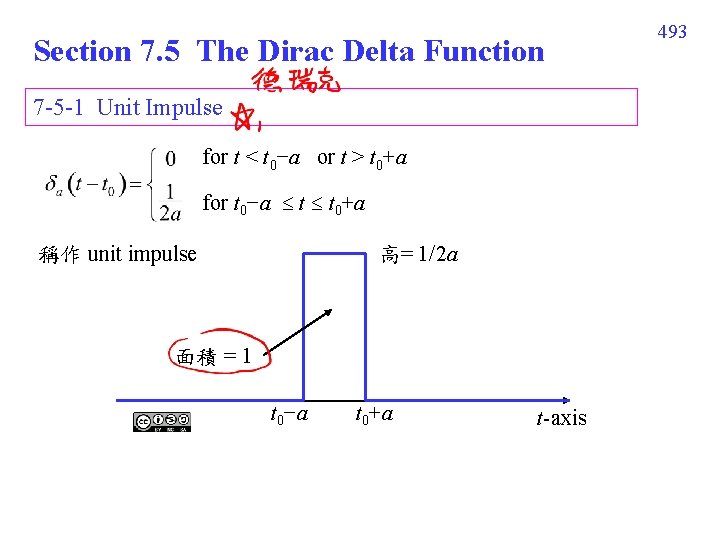
Section 7. 5 The Dirac Delta Function 7 -5 -1 Unit Impulse for t < t 0−a or t > t 0+a for t 0−a t t 0+a 稱作 unit impulse 高= 1/2 a 面積 = 1 t 0−a t 0+a t-axis 493

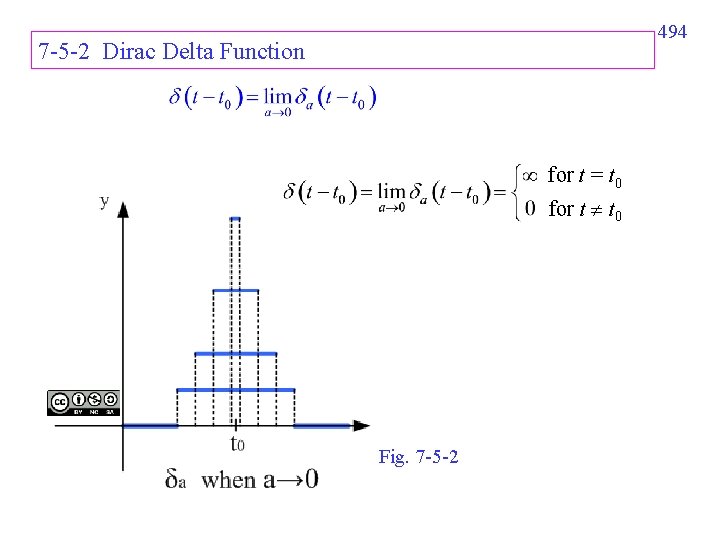
494 7 -5 -2 Dirac Delta Function for t = t 0 for t t 0 Fig. 7 -5 -2

7 -5 -3 Properties of the Dirac Delta Function (1) Integration (2) Sifting when t 0 [p, q] Proof: 當 a 很小的時候,f(t) f(t 0) for t 0−a t t 0+a 495

(3) Laplace transform of (t − t 0) when t 0 > 0 Proof: (from the sifting property) (4) Relation with the unit step function 496

497 7 -5 -4 Example 1(a) (text page 319) 0 t < 2 t 2

498 7 -5 -5 幾個名詞 where (1) w(t) = L− 1{W(s)} 稱作 weight function 或 impulse response Note: When Q(s) = 0 (no initial condition) and G(s) = 1 (g(t) = (t)), Y(s) = W(s), y(t) = w(t). (2) 許多文獻把 Dirac delta function (t − t 0) 亦稱作 delta function , impulse function,或 unit impulse function


Section 7 -6 Systems of Linear Differential Equations Chapter 7 的應用題 比較:類似的問題,也曾經在 Section 4 -9 出現過 7 -6 -1 雙彈簧的例子 500


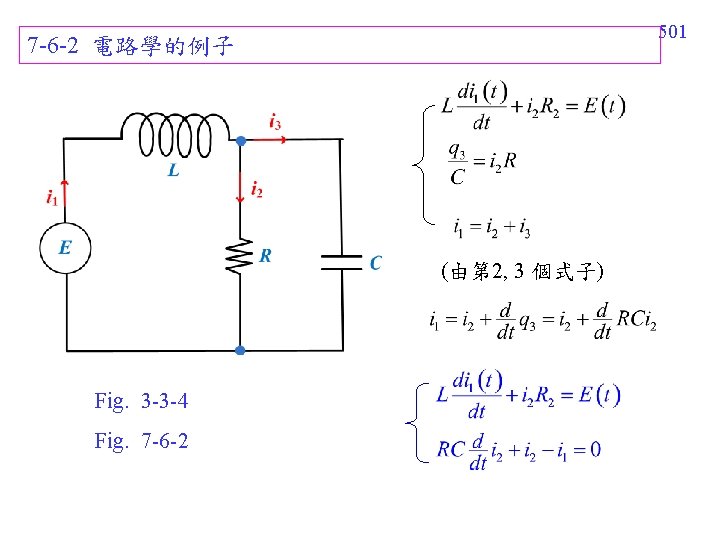
502 Example 2 (text page 323) E(t) = 60 V, L = 1 H, R = 50 , C = 10− 4 F, i 1(t) = i 2(t) = 0 ………. . (式 1) …. . . (式 2) (式 1) × 1 + (式 2) × s


504

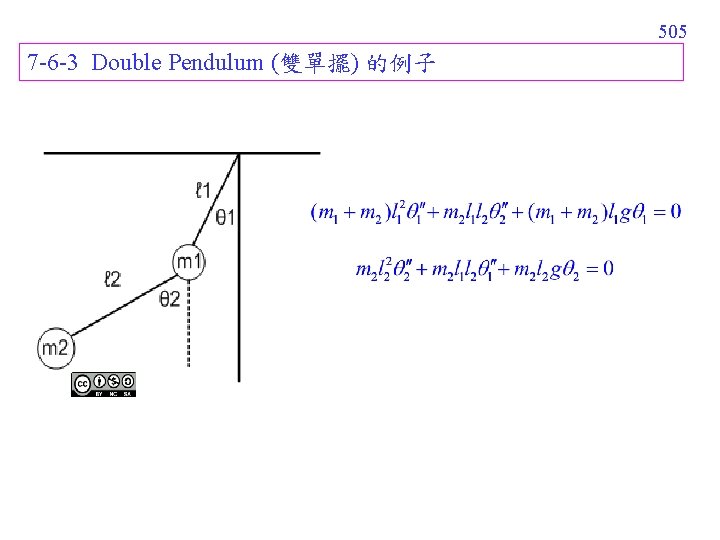
505 7 -6 -3 Double Pendulum (雙單擺) 的例子

506 Example 3 (text page 324) m 1 = 3, m 2 = 1, l 1 = 12 = 16, 1(0) = 1, 2(0) = 1, '1(0) = 0, '2(0) = 0 Laplace
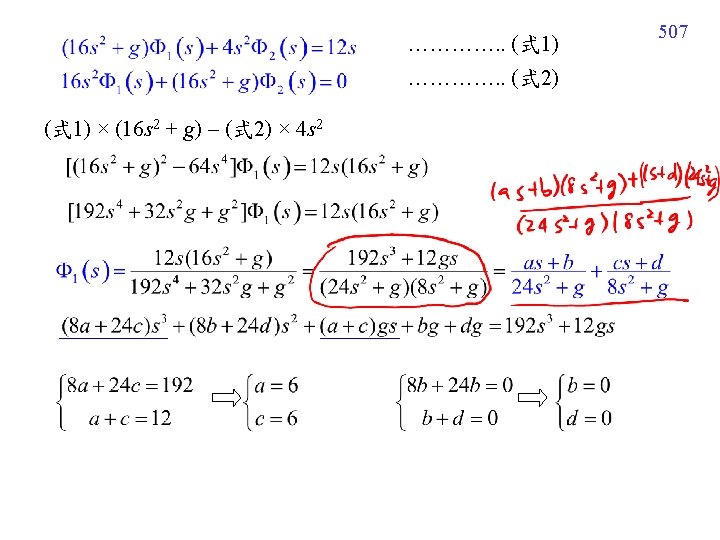

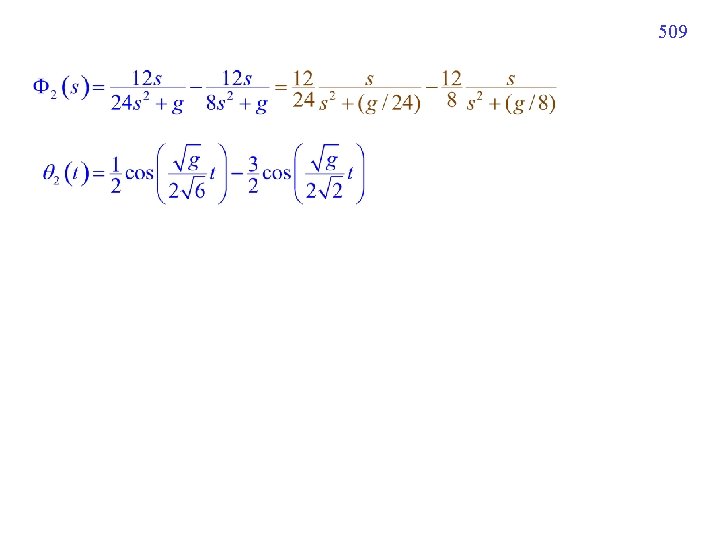
509



Review of Chapter 7 (1) Laplace transform 定義 Inverse Laplace transform If then (2) 7 大transform pairs (看講義 page 423) and f(t) is piecewise continuous of exponential order 512

513 transform pairs 補充 f(t) F(s) tsin(kt) tcos(kt) tsinh(kt) tcosh(kt) u(t a) 0 1 a b 0 f (t) = f (t+2 a)

514 (3) 7 大 properties input (1) Differentiation (Sec 7 -2) (2) Multiplication by t (Sec 74) (3) Integration (Sec 7 -4) (續) Laplace transform

515 input (4) Multiplication by exp (Sec 73) (5. 1) Translation (Sec 7 -3) (5. 2) Translation (Sec 7 -3) (6) Convolution (Sec 7 -4) (7) Periodic Input (Sec 7 -4) f(t) = f(t + T) Laplace transform

516 Properties 補充 input Scaling f(t / a) Multiple Integrations Integration for s f(t) / t Laplace transform a. F(as)

(4) 簡化運算的方法 分式分解 (see pages 442 -447) Initial conditions (see pages 455, 456) (5) Delta function 的四大性質 Pages 495, 496 517

518 (6) General solutions Laplace transform 的 general solution,可以用 initial conditions 來表示。 例子: 用 Laplace transform : 用Sec. 4 -3 的 方法解出


520 Exercise for Practice Sec. 7 -1: 5, 8, 9, 18, 32, 33, 36, 38, 41, 49, 54, 55, 56, 57, 58 Sec. 7 -2: 11, 20, 23, 26, 27, 30, 41, 45, 46, 49 Sec. 7 -3: 10, 16, 19, 20, 24, 35, 42, 44, 56, 58, 62, 64, 68, 70, 74, 83 Sec. 7 -4: 8, 13, 29, 32, 34, 42, 47, 50, 56, 57, 58, 63, 65, 67, 70 Sec. 7 -5: 5, 6, 8, 11, 12, 17 Sec. 7 -6: 8, 11, 12, 14, 15 Review 7: 12, 24, 25, 29, 38, 40, 41, 44, 45, 46