Chapter 11 Matrix Inverse and Condition Matrix Inverse

![Matrix Inverse z How do we get inverse [A] 1? z One way is Matrix Inverse z How do we get inverse [A] 1? z One way is](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-2.jpg)
![Matrix Inverse z[A] 1 = [ I ] z. Use LU factorization to find Matrix Inverse z[A] 1 = [ I ] z. Use LU factorization to find](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-3.jpg)
![Matrix Inverse z. Forward Substitution [L][Y] = [ I ] Matrix Inverse z. Forward Substitution [L][Y] = [ I ]](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-4.jpg)
![Matrix Inverse zback Substitution [U][X] = [ Y ] Matrix Inverse zback Substitution [U][X] = [ Y ]](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-5.jpg)

![Example: Matrix Inverse » A=[-19 20 -6; -12 13 -3; 30 -30 12] » Example: Matrix Inverse » A=[-19 20 -6; -12 13 -3; 30 -30 12] »](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-7.jpg)



![Matrix Condition Number Ø Condition number defined in terms of matrix norms Ø Cond[A] Matrix Condition Number Ø Condition number defined in terms of matrix norms Ø Cond[A]](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-12.jpg)




- Slides: 16

Chapter 11 Matrix Inverse and Condition
![Matrix Inverse z How do we get inverse A 1 z One way is Matrix Inverse z How do we get inverse [A] 1? z One way is](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-2.jpg)
Matrix Inverse z How do we get inverse [A] 1? z One way is through LU decomposition and backsubstitution z. Solve [A]{xi} = {bi} with Sequentially! z Put together x’s to get [A]-1 ={x 1, x 2, x 3, x 4}
![Matrix Inverse zA 1 I z Use LU factorization to find Matrix Inverse z[A] 1 = [ I ] z. Use LU factorization to find](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-3.jpg)
Matrix Inverse z[A] 1 = [ I ] z. Use LU factorization to find [X] = [A] 1 z. LU decomposition: [A] = [L][U] z. Forward substitution: [L][Y] = [ I ] z. Back substitution: [U][X] = [Y]
![Matrix Inverse z Forward Substitution LY I Matrix Inverse z. Forward Substitution [L][Y] = [ I ]](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-4.jpg)
Matrix Inverse z. Forward Substitution [L][Y] = [ I ]
![Matrix Inverse zback Substitution UX Y Matrix Inverse zback Substitution [U][X] = [ Y ]](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-5.jpg)
Matrix Inverse zback Substitution [U][X] = [ Y ]

function x % Function % L --> % U --> % B --> = LU_Solve_Gen(L, U, B) to solve the equation L U x = B Lower triangular matrix (1's on diagonal) Upper triangular matrix Right-hand-side matrix [n n 2] = size(L); [m 1 m] = size(B); % Solve L d = B using forward substitution for j = 1 : m d(1, j) = B(1, j); for i = 2 : n d(i, j) = B(i, j) - L(i, 1: i-1) * d(1: i-1, j); end % SOlve U x = d using back substitution for j = 1 : m x(n, j) = d(n, j) / U(n, n); for i = n-1 : 1 x(i, j) = (d(i, j) - U(i, i+1: n) * x(i+1: n, j)) / U(i, i); end
![Example Matrix Inverse A19 20 6 12 13 3 30 30 12 Example: Matrix Inverse » A=[-19 20 -6; -12 13 -3; 30 -30 12] »](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-7.jpg)
Example: Matrix Inverse » A=[-19 20 -6; -12 13 -3; 30 -30 12] » B=eye(3) A = B = -19 -12 30 20 13 -30 -6 -3 12 1 0 0 0 1 » [L, U]=LU_factor(A); » x=LU_solve_gen(L, U, B) L = x = 1. 0000 0. 6316 -1. 5789 0 1. 0000 4. 2857 0 0 1. 0000 -10. 0000 -8. 0000 5. 0000 3. 0000 2. 5000 -1. 1667 » inv(A) U = -19. 0000 0 0 11. 0000 9. 0000 -5. 0000 20. 0000 0. 3684 0. 0000 -6. 0000 0. 7895 -0. 8571 ans = 11. 0000 9. 0000 -5. 0000 MATLAB function -10. 0000 -8. 0000 5. 0000 3. 0000 2. 5000 -1. 1667

Error Analysis and System Condition z The matrix inverse provides a means to discern whether a system is ill-conditioned 1. Normalize rows of matrix [A] to 1. If the elements of [A] 1 are >> 1, the matrix is likely ill-conditioned 2. If [A] 1[A] is not close to [ I ], the matrix is probably ill-conditioned 3. If ([A] 1) 1 is not close to [A], the matrix is ill -conditioned

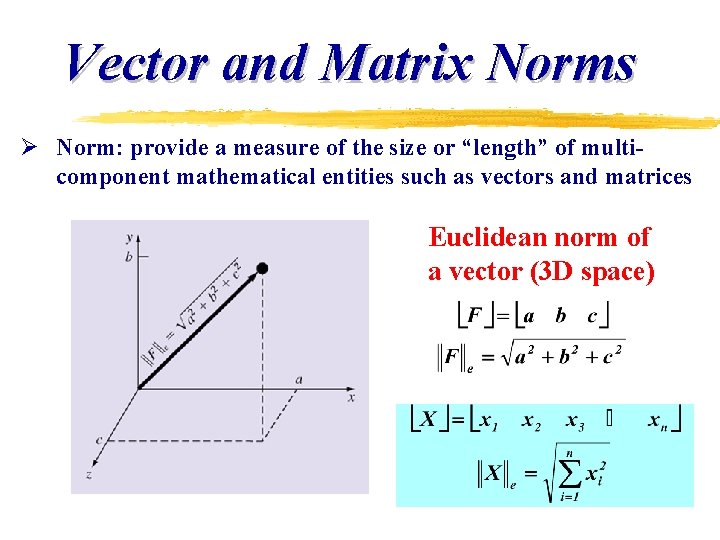
Vector and Matrix Norms Ø Norm: provide a measure of the size or “length” of multicomponent mathematical entities such as vectors and matrices Euclidean norm of a vector (3 D space)

Matrix Norm z For n n matrix, the Frobenius norm z Frobenius norm provides a single value to quantify the size of matrix [A] z Other alternatives – p norms for vectors p = 2 : Euclidean norm

Vector and Matrix Norms z Vector norms ( p-norms) Sum of absolute values z Matrix norms Maximum-magnitude or uniform-vector norm Column-sum norm Row-sum norm
![Matrix Condition Number Ø Condition number defined in terms of matrix norms Ø CondA Matrix Condition Number Ø Condition number defined in terms of matrix norms Ø Cond[A]](https://slidetodoc.com/presentation_image/1f1f6b099f770a2ebb3342b4524238a6/image-12.jpg)
Matrix Condition Number Ø Condition number defined in terms of matrix norms Ø Cond[A] is great than or equal to 1 Ø Matrix A is ill-conditioned if Cond[A] >> 1 Relative error of the norm Ø If [A] has 10 7 rounding error and Cond[A] = 105, then the solution [X] may be valid to only 10 2

Matrix Condition Evaluation z Hilbert matrix – notoriously ill-conditioned Normalization z Row-sum norm (last row has the largest sum)

Matrix Condition Evaluation z 5 5 Hilbert matrix z Condition number

MATLAB Norms and Condition Numbers >> A=[1 1/2 1/3 1/4 1/5; 1 2/3 2/4 2/5 2/6; 1 3/4 3/5 3/6 3/7; 1 4/5 4/6 4/7 4/8; 1 5/6 5/7 5/8 5/9]; >> Ainv = inv(A) Ainv = 25 -150 350 -350 126 -300 2400 -6300 6720 -2520 1050 -9450 26460 -29400 11340 -1400 13440 -39200 44800 -17640 630 -6300 18900 -22050 8820 >> norm(A, inf) ans = 3. 7282 >> norm(Ainv, inf) ans = 1. 1648 e+005 >> cond(A, inf) ans = 4. 3426 e+005 >> norm(X, p) >> cond(A, 'fro') p-norm ans = >> cond(X, p) 2. 7944 e+005 >> cond(A) Frobenius norm >> Cond(A, ’fro’) ans = 2. 7746 e+005 Spectral norm >> cond(A)

CVEN 302 -501 Homework No. 7 z Chapter 10 z Prob. 10. 4(20), 10. 5(20) both using LU decomposition (hand calculation only, hand partial pivoting if necessary), Prob. 10. 8 a)&b) (20). z Chapter 11 z Prob. 11. 2 (15), 11. 3 a) & b) (20) (Hand Calculations) z Prob. 11. 6 (25) (Hand Calculations; Check your solutions using MATLAB) z Due Monday 10/13/08 at the beginning of the period