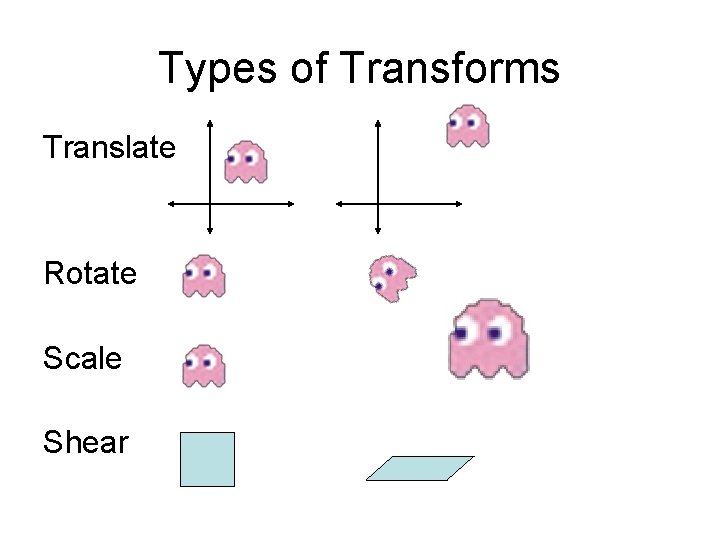
Transforms Types of Transforms Translate Rotate Scale Shear

Transforms

Types of Transforms Translate Rotate Scale Shear

Affine Transform Math • Transforms are cumulative • Transforms change the whole world view • Order matters!

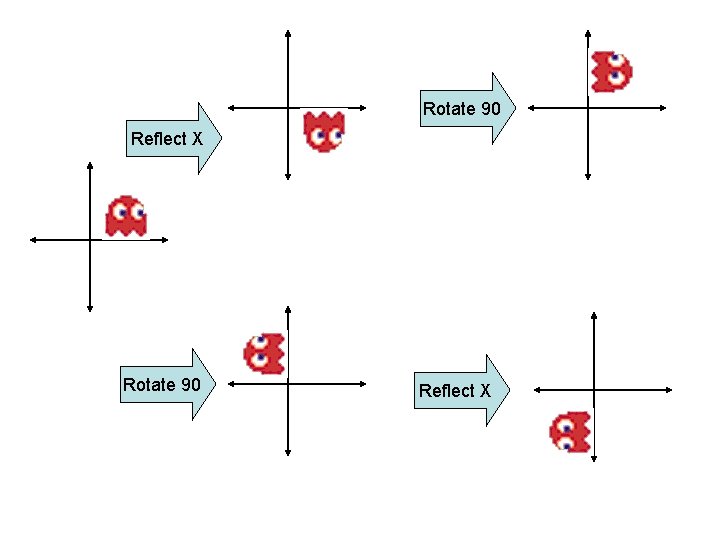
Rotate 90 Reflect X

Making Shapes work together • Create an object that has state variables corresponding to its parts • Draw from the center of the overall object • Perform transforms: 1. translate to center of overall object 2. rotate if wanted 3. scale/shear if wanted

Matrices • Rectangular arrangement of numbers • [1 2 3] 2 -3 0 3 7 -1 • Dimensions • Diagonal • Transpose: interchange rows and cols • Identity: Square matrix, diagonal is ones, rest is zeros

Matrix Operations • Adding and subtracting: matrices must have same dimensions • Add or subtract element-wise [1 2 3] + [4 5 6] = [5 7 9] • Scalar multiplication: multiply all elements by the scalar 2 * [1 2 3] = [2 4 6]

Multiplying Matrices 3 [4 5 6] x 2 = 4*3 + 5*2 + 6*1 = [28] 1 (m x n) x (n x p) yields (mxp) Even if the matrices are square, multiplication is not commutative

Matrices and Graphics • A point can be described (3, 2) using a vector: p = (x, y) p = xi+yj • Or a matrix: [x y] • Transposes are matrices that get postmultiplied to the point to produce a new point.

Scaling • Multiply by the matrix a 0 where a is the scale 0 b factor in the x direction, and b is the scale factor in the y direction • If a and b are the same, it’s like multiplying by a scalar. (Balanced or Uniform scaling)

Scaling (12, 8) (3, 2) [3 2] 4 0 = [12 8] 0 4

Reflecting • Reflection in the x–axis: 1 0 0 -1 • Reflection in the y–axis: -1 0 0 1 • In general, multiplying by negative numbers combines a reflection and a scale.

Reflection [ 3 2] -1 0 = [-3 -2] 0 -1 (3, 2) (-3, -2)

Rotations: Searching for a Pattern -1 0 rotates through 180 degrees 0 -1 (pi radians) 1 0 rotates through 360 degrees 0 1 (2 pi radians) 0 1 causes a rotation of 90 degrees -1 0 (pi/2 radians) 0 -1 causes a rotation of 270 degrees 1 0 (3 pi/2 radians)

In general… • The pattern emerges: To rotate through an angle Ө, multiply by cos Ө sin Ө -sin Ө cos Ө

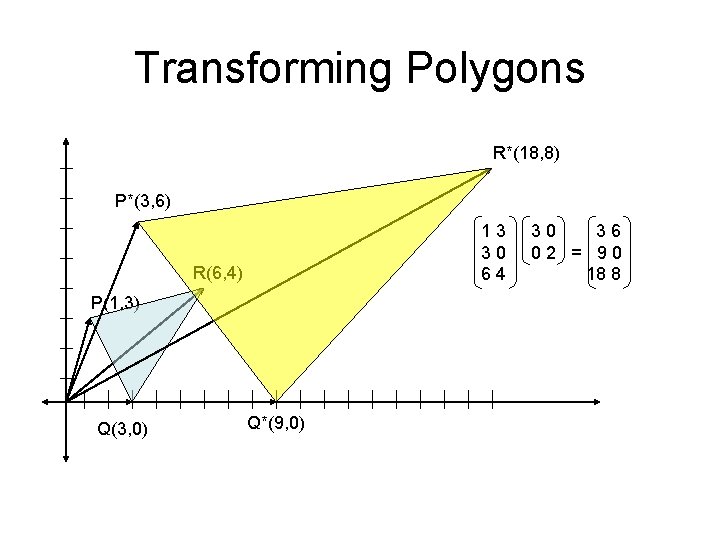
Transforming Polygons • To transform a line, transform its end points and connect the new points. • Polygons are collections of lines. • Multiplying several points is the same as making a matrix where each point is a row. • True for Affine Transformations – preserves points on line and parallelism – preserves proportions (i. e. , the midpoint remains the midpoint)

Transforming Polygons R*(18, 8) P*(3, 6) 13 30 64 R(6, 4) P(1, 3) Q(3, 0) Q*(9, 0) 30 36 02 = 90 18 8

Multiple transformations • Order in transformations matters. • Matrix multiplication is not commutative!

Translations • To translate, we add rather than multiply matrices. • To shift a point over by a in the x direction and b in the y direction, add the matrix [ a b]

Transformations [ 3 2 ] + [ 2 4] = [5 6] (5, 6) (2, 4) (3, 2)

Homogeneous Coordinates • You can’t use a 2 x 2 multiplication matrix to model translation. Bummer! • But, we can add a third dimension of homogeneous coordinates, and now all 2 D transformations can be expressed in a 3 x 3 matrix.

Homogeneous Translation 1. Add a 1 to the point vector [3 2 1] = (3, 2) 2. To translate over 2 and up 4, multiply by 1 0 0 0 1 0 2 4 1 [3 2 1] 1 0 0 0 1 0 2 4 1 = [5 6 1]

Homogeneous Scale • Scale by a in x direction and b in y a 0 0 0 b 0 0 0 1 • Reflect in x-axis: 1 0 0 0 -1 0 0 0 1

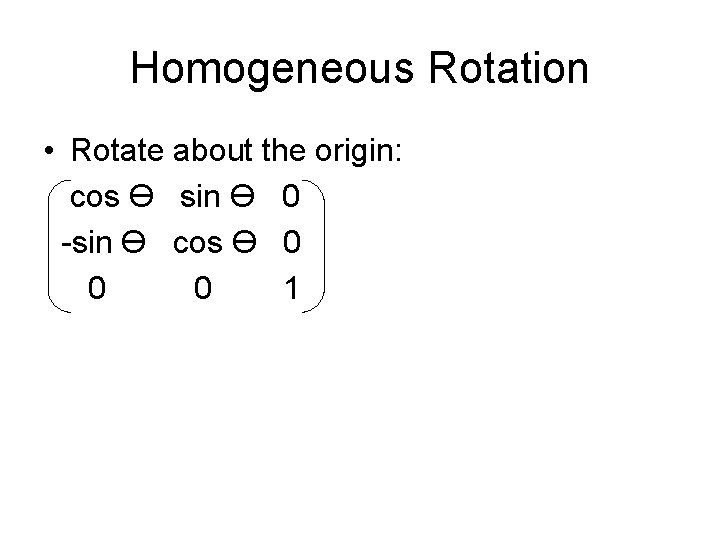
Homogeneous Rotation • Rotate about the origin: cos Ө sin Ө 0 -sin Ө cos Ө 0 0 0 1

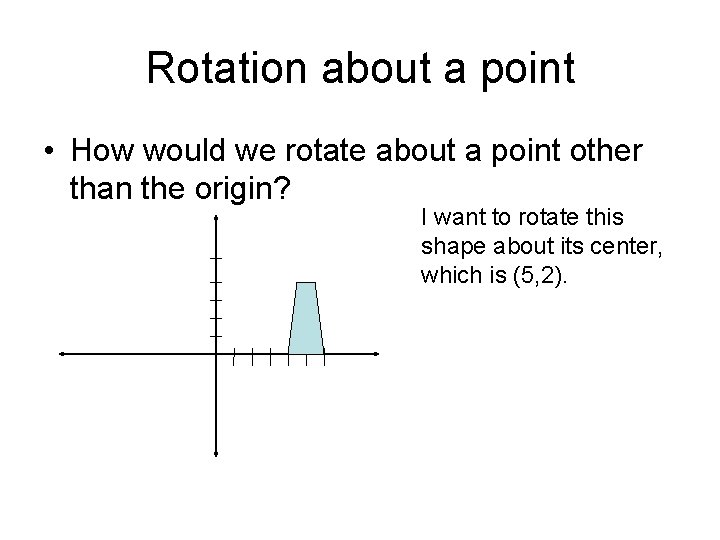
Rotation about a point • How would we rotate about a point other than the origin? I want to rotate this shape about its center, which is (5, 2).

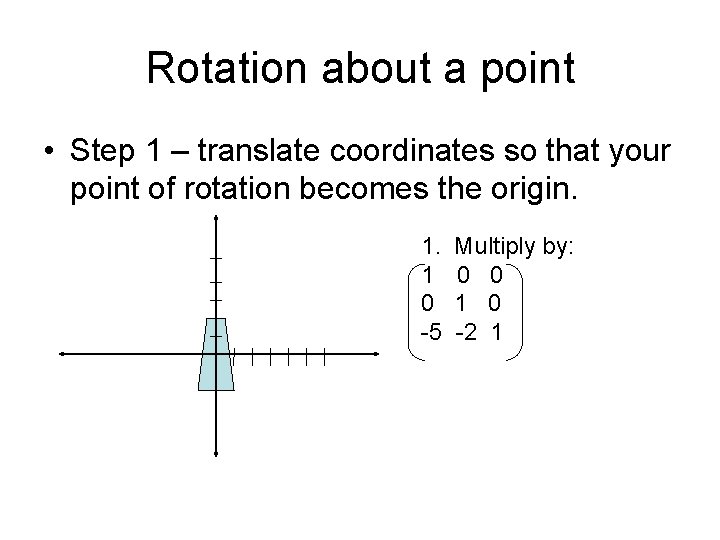
Rotation about a point • Step 1 – translate coordinates so that your point of rotation becomes the origin. 1. 1 0 -5 Multiply by: 0 0 1 0 -2 1

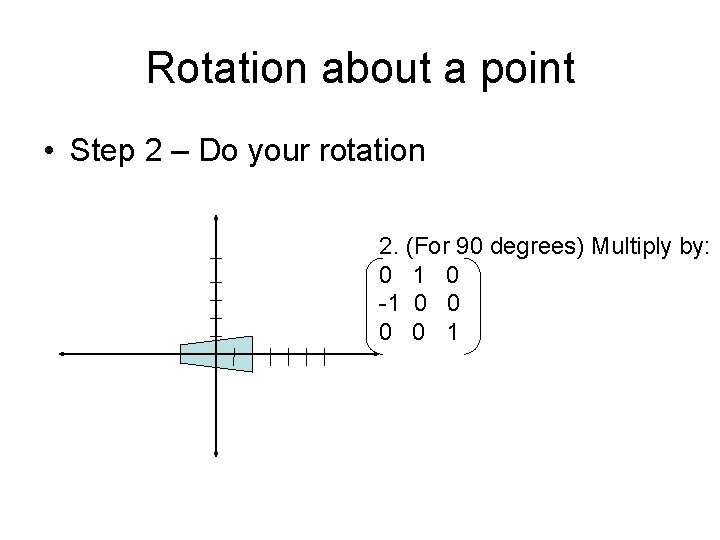
Rotation about a point • Step 2 – Do your rotation 2. (For 90 degrees) Multiply by: 0 1 0 -1 0 0 1

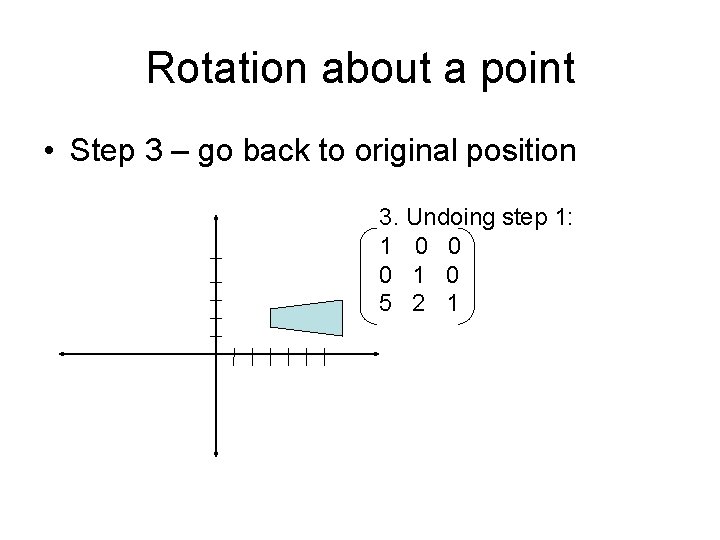
Rotation about a point • Step 3 – go back to original position 3. Undoing step 1: 1 0 0 0 1 0 5 2 1

3 D • How do you think it is done in 3 D?