Review Short range force Pauli Principle Shell structure















![Simple example of dynamical symmetries, group chain, degeneracies [H, J 2 ] = [H, Simple example of dynamical symmetries, group chain, degeneracies [H, J 2 ] = [H,](https://slidetodoc.com/presentation_image_h/c2a009a29149fc861c4a9a599c14f6b6/image-26.jpg)
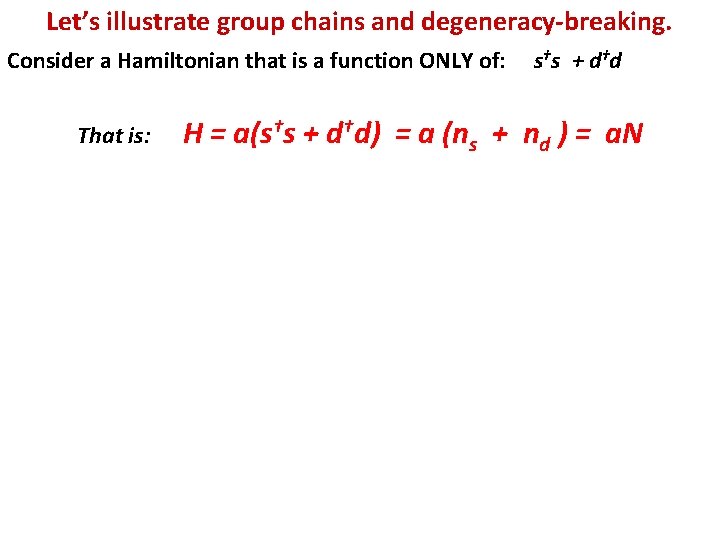


















- Slides: 71

Review • Short range force, Pauli Principle Shell structure, magic numbers, concept of valence nucleons • Residual interactions favoring of 0+ coupling: 0+ ground states for all even-even nuclei • Concept of seniority lowest states have low seniority, huge simplification (n-body calculations often reduce to 2 -body !) • constant g factors, constant energies in singly magic or near magic nuclei, parabolic B(E 2) systematics, change in sign of quadrupole moments (prolate-oblate shapes) across a shell

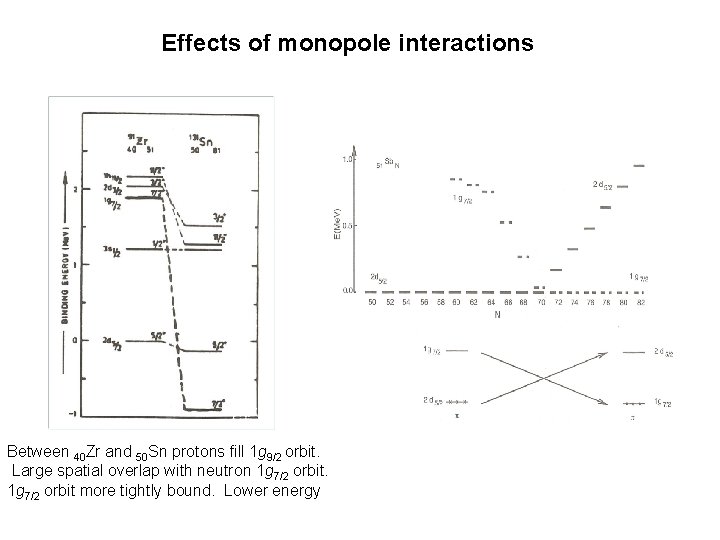
Effects of monopole interactions Between 40 Zr and 50 Sn protons fill 1 g 9/2 orbit. Large spatial overlap with neutron 1 g 7/2 orbit more tightly bound. Lower energy

Lecture 3 Collective behavior in nuclei and collective models

How does structure evolve? • Benchmarks – Magic nuclei – spherical, stiff – Nuclei with only one kind of valence nucleon: like the 2 -particle case – Nuclei with both valence protons and neutrons: mixing of configurations, complex wave functions with components from every configuration (~10 big). – Is there another way? YES !!! – Macroscopic perspective. Many-body approach, collective coordinates, modes

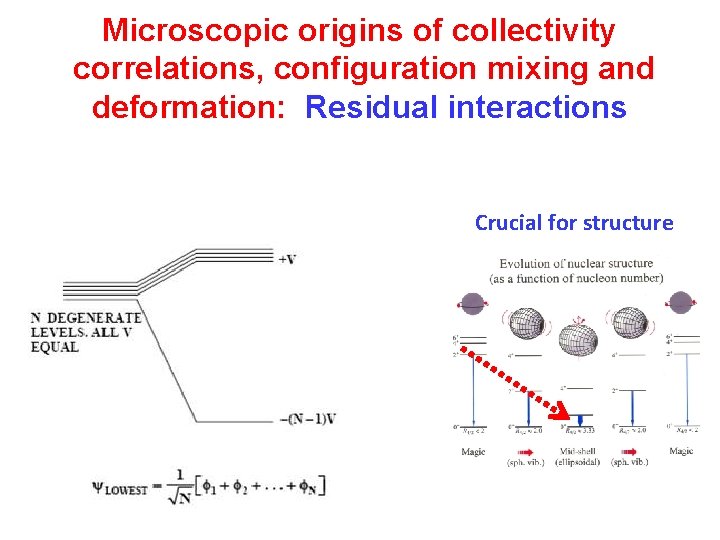
Microscopic origins of collectivity correlations, configuration mixing and deformation: Residual interactions Crucial for structure

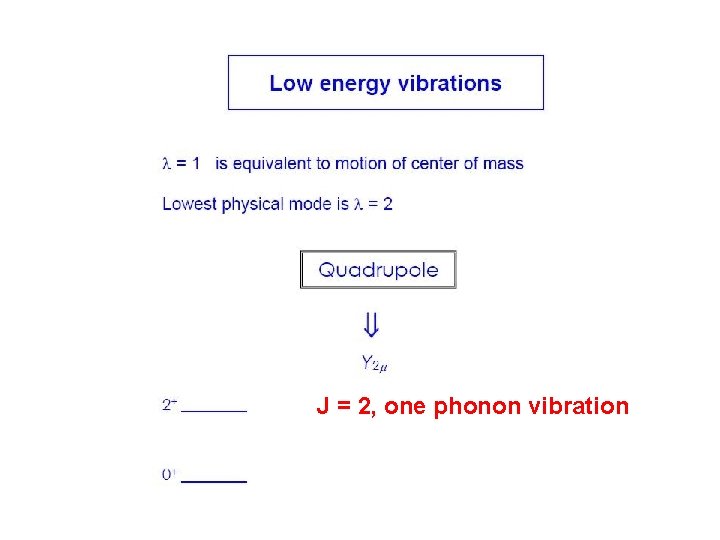
J = 2, one phonon vibration

More than one phonon? What angular momenta? M-scheme for bosons


Deformed Nuclei • What is different about non-spherical nuclei? • They can ROTATE !!! • They can also vibrate – For axially symmetric deformed nuclei there are two low lying vibrational modes called b gand g • So, levels of deformed nuclei consist of the ground state, and vibrational states, with rotational sequences of states (rotational bands) built on top of them.

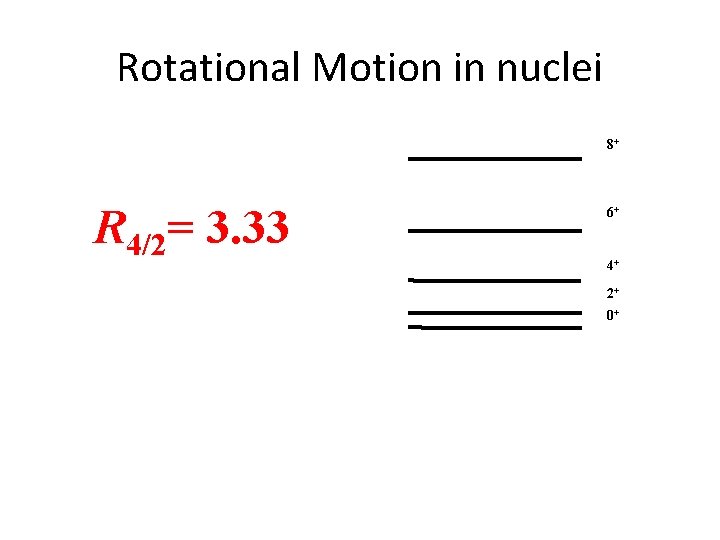
Rotational Motion in nuclei 8+ E(I) ( ħ 2/2 I )J(J+1) R 4/2= 3. 33 6+ 4+ 2+ 0+

Paradigm The value of paradigms 6+ 690 4+ 330 2+ 0+ 100 ? E (ke. V) Exp. 700 333 Centrifugal stretching 100 0 0 J Amplifies structural Benchmark differences Interpretation without rotor paradigm Rotor J(J + 1) Deviations Identify additional degrees of freedom

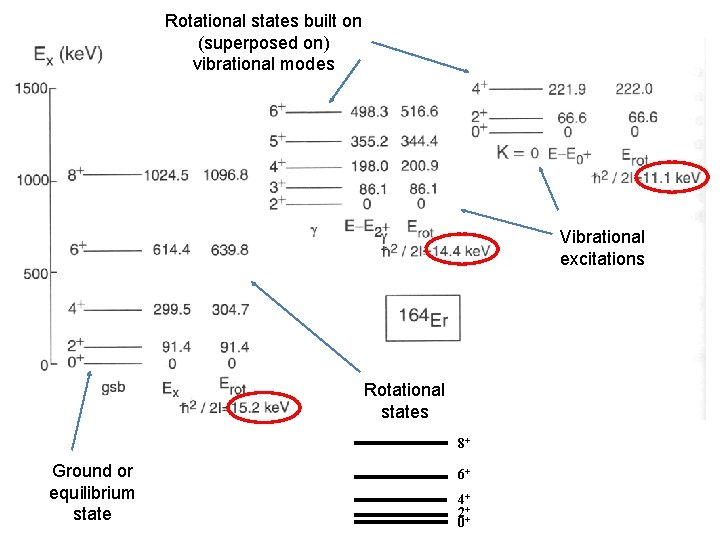
Rotational states built on (superposed on) vibrational modes Vibrational excitations Rotational states 8+ Ground or equilibrium state 6+ 4+ 2++ 0

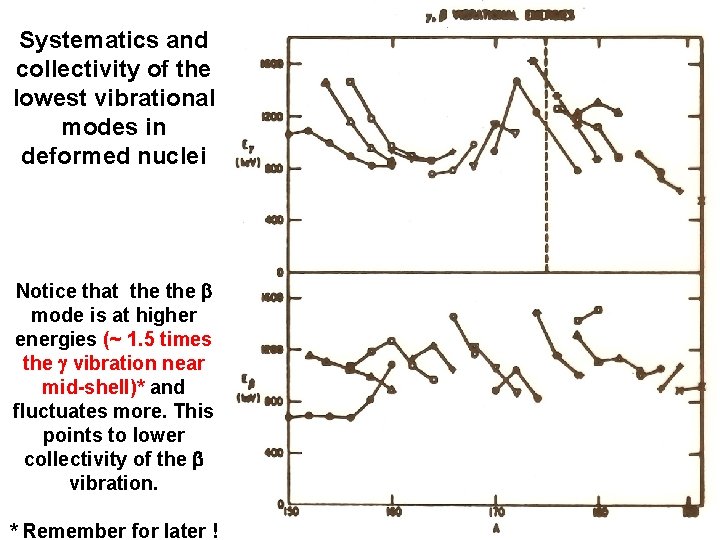
Systematics and collectivity of the lowest vibrational modes in deformed nuclei Notice that the b mode is at higher energies (~ 1. 5 times the g vibration near mid-shell)* and fluctuates more. This points to lower collectivity of the b vibration. * Remember for later !


How can we understand collective behavior • Do microscopic calculations, in the Shell Model or its modern versions, such as with density functional theory or Monte Carlo methods. These approaches are making amazing progress in the last few years. Nevertheless, they often do not give an intuitive feeling for the structure calculated. • Collective models, which focus not on the particles but the structure and symmetries of the many-body, macroscopic system itself. They are not predictive in the same way as microscopic calculations but they can reveal coherent behavior more clearly in many cases. • We will illustrate collective models with the IBA, historically, by far the most successful and parameter-efficient collective model.

IBA – A Review and Practical Tutorial F. Iachello and A. Arima Drastic simplification of shell model · Valence nucleons · Only certain configurations · Simple Hamiltonian – interactions “Boson” model because it treats nucleons in pairs 2 fermions boson

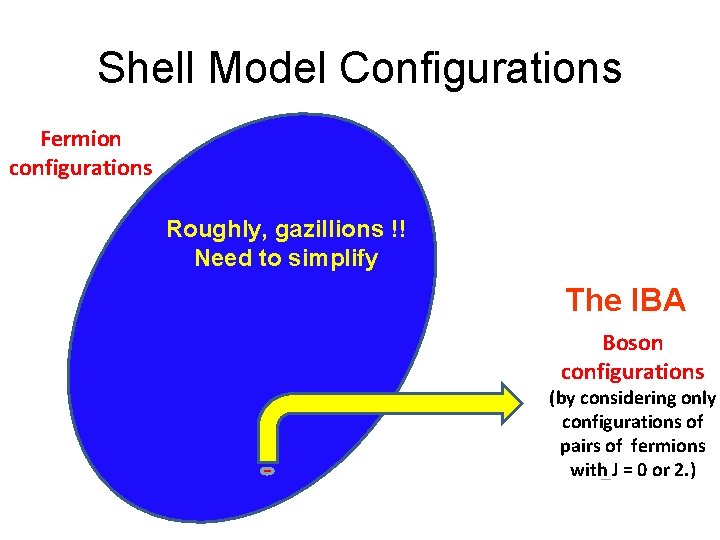
Shell Model Configurations Fermion configurations Roughly, gazillions !! Need to simplify The IBA Boson configurations (by considering only configurations of pairs of fermions with J = 0 or 2. )

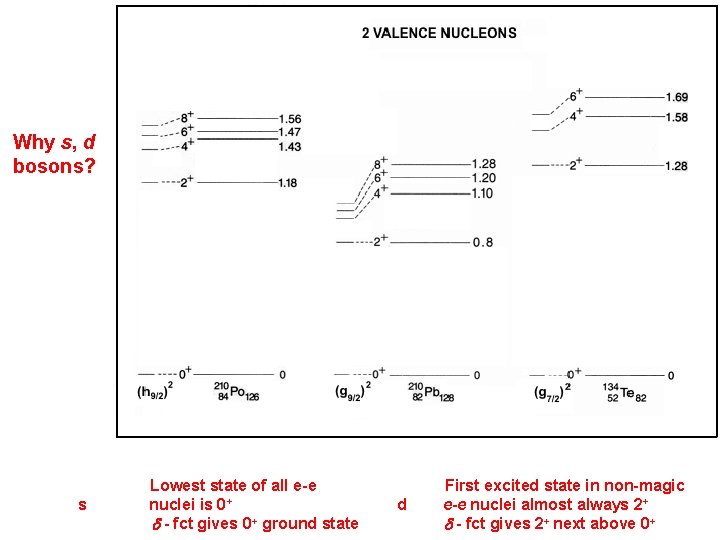
Why s, d bosons? s Lowest state of all e-e nuclei is 0 + - fct gives 0+ ground state d First excited state in non-magic e-e nuclei almost always 2+ - fct gives 2+ next above 0+

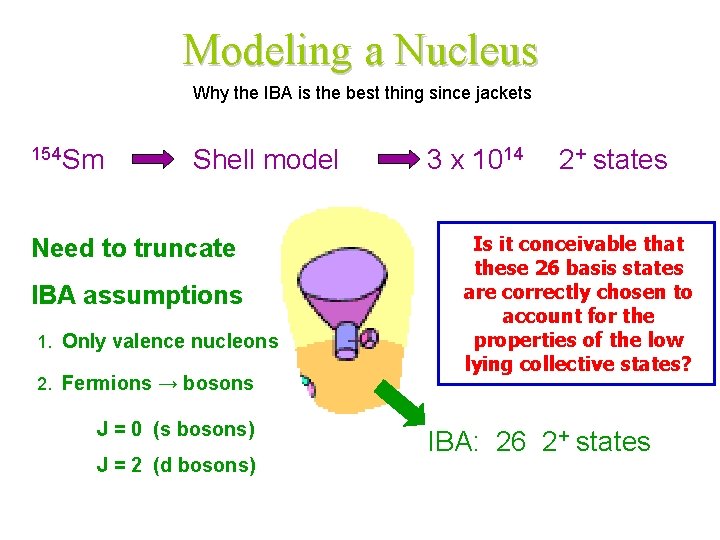
Modeling a Nucleus Why the IBA is the best thing since jackets 154 Sm Shell model Need to truncate IBA assumptions 1. Only valence nucleons 2. Fermions → bosons J = 0 (s bosons) J = 2 (d bosons) 3 x 1014 2+ states Is it conceivable that these 26 basis states are correctly chosen to account for the properties of the low lying collective states? IBA: 26 2+ states

Note key point: Bosons in IBA are pairs of fermions in valence shell Number of bosons for a given nucleus is a fixed number N = 6 5 = N NB = 11 Basically the IBA is a Hamiltonian written in terms of s and d bosons and their interactions. It is written in terms of boson creation and destruction operators. Let’s briefly review their key properties.

Review of phonon creation and destruction operators What is a creation operator? Why useful? A) Bookkeeping – makes calculations very simple. B) “Ignorance operator”: We don’t know the structure of a phonon but, for many predictions, we don’t need to know its microscopic basis. is a b-phonon number operator. For the IBA a boson is the same as a phonon – think of it as a collective excitation with ang. mom. 0 (s) or 2 (d).

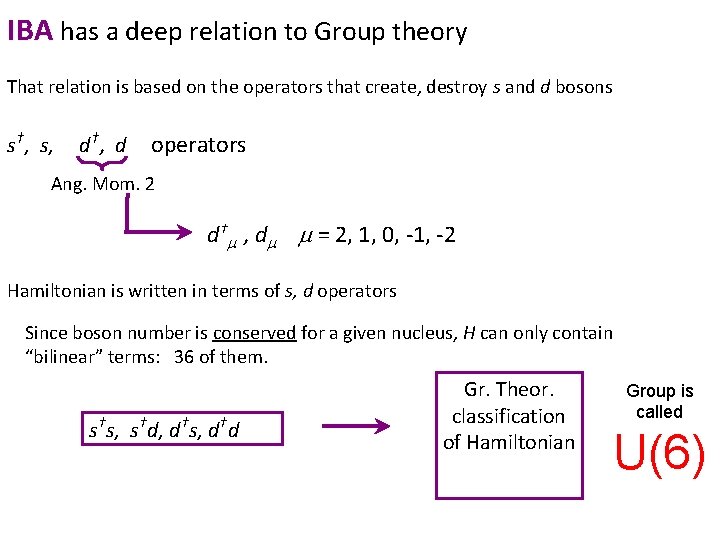
IBA has a deep relation to Group theory That relation is based on the operators that create, destroy s and d bosons s†, s, d †, d operators Ang. Mom. 2 d† , d = 2, 1, 0, -1, -2 Hamiltonian is written in terms of s, d operators Since boson number is conserved for a given nucleus, H can only contain “bilinear” terms: 36 of them. s†s, s†d, d†s, d†d Gr. Theor. classification of Hamiltonian Group is called U(6)

Brief, simple, trip into the Group N Th intr ext eo odof 8 the Theory ry uc slid IBA dif disc rele tion es g fic us van to ive yo ult sio t t th an e DON’T BE SCARED u o o n the w r to of th Gr i for rest ll be o fa the e IBA oup abto understand st, se all the a wi You 5 do not need. If n i l ll h mi y s the egett thedidea the w o t n details but try to of o a n an ve ute y. J un ’t w o s. of groups to degeneracies of d relation t d u h o e ca st Iquantum e r n r ry, s s levels and numbers t mo n l a e t a re ook slid ny c ke a and es as de a tai t th on e, y nap l if emapplication ouof Group Theory is t h A more intuitive name for this ew yo l a u w te eb r an i. Algebras” “Spectrum Generating t. n

Concepts of group theory First, some fancy words with simple meanings: Generators, Casimirs, Representations, conserved quantum numbers, degeneracy splitting Generators of a group: Set of operators , Oi that close on commutation. [ Oi , Oj ] = Oi Oj - Oj Oi = Ok i. e. , their commutator gives back 0 or a member of the set For IBA, the 36 operators s†s, d†s, s†d, d†d are generators of the group U(6). Generators : define and conserve some quantum number. ex: Ex. : 36 Ops of IBA all conserve total boson number N = s †s + d † = ns + nd e. g: Operator that commutes with all the generators of a group. Therefore, its Casimir: eigenstates have a specific value of the q. # of that group. The energies are defined solely in terms of that q. #. N is Casimir of U(6). Representations of a group: The set of degenerate states with that value of the q. #. A or: Hamiltonian written solely in terms of Casimirs can be solved analytically

Sub-groups: Subsets of generators that commute among themselves. e. g: d†d 25 generators—span U(5) They conserve nd (# d bosons) Set of states with same nd are the representations of the group [ U(5)] Summary to here: Generators: commute, define a q. #, conserve that q. # Casimir Ops: commute with a set of generators Conserve that quantum # A Hamiltonian that can be written in terms of Casimir Operators is then diagonal for states with that quantum # Eigenvalues can then be written ANALYTICALLY as a function of that quantum #
![Simple example of dynamical symmetries group chain degeneracies H J 2 H Simple example of dynamical symmetries, group chain, degeneracies [H, J 2 ] = [H,](https://slidetodoc.com/presentation_image_h/c2a009a29149fc861c4a9a599c14f6b6/image-26.jpg)
Simple example of dynamical symmetries, group chain, degeneracies [H, J 2 ] = [H, J Z ] = 0 J, M constants of motion
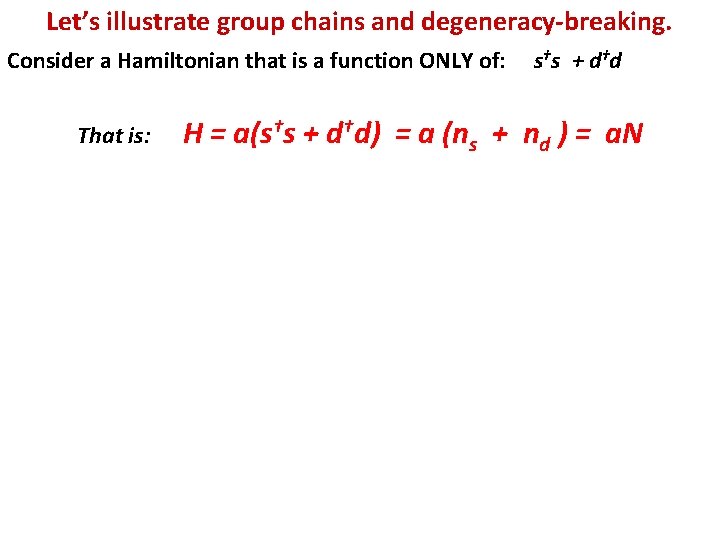
Let’s illustrate group chains and degeneracy-breaking. Consider a Hamiltonian that is a function ONLY of: That is: s †s + d †d H = a(s†s + d†d) = a (ns + nd ) = a. N In H, the energies depend ONLY on the total number of bosons, that is, on the total number of valence nucleons. ALL the states with a given N are degenerate. That is, since a given nucleus has a given number of bosons, if H were the total Hamiltonian, then all the levels of the nucleus would be degenerate. This is not very realistic (!!!) and suggests that we should add more terms to the Hamiltonian. I use this example though to illustrate the idea of successive steps of degeneracy breaking being related to different groups and the quantum numbers they conserve. The states with given N are a “representation” of the group U(6) with the quantum number N. U(6) has OTHER representations, corresponding to OTHER values of N, but THOSE states are in DIFFERENT NUCLEI (numbers of valence nucleons).

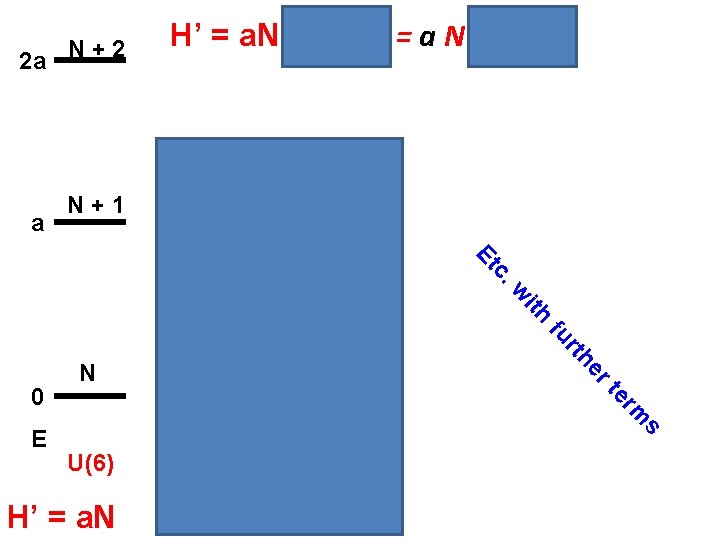
H’ = H + b d†d = a. N + b nd Now, add a term to this Hamiltonian: Now the energies depend not only on N but also on nd States of a given nd are now degenerate. They are “representations” of the group U(5). States with different nd are not degenerate

2 a N + 2 a H’ = a. N + b d†d = a N + b nd N+1 b d †d s + m er H’ = a. N U(5) rt he U(6) nd rt E fu 0 ith 0 w 0 N c. Et b 2 1 2 b

OK, here’s the key point : Concept of a Dynamical Symmetry Sp N ec tru m ge ne rat ing alg eb ra !!

OK, here’s what you need to remember from the Group Theory • Group Chain: U(6) U(5) O(3) • A dynamical symmetry corresponds to a certain structure/shape of a nucleus and its characteristic excitations. The IBA has three dynamical symmetries: U(5), SU(3), and O(6). • Each term in a group chain representing a dynamical symmetry gives the next level of degeneracy breaking. • Each term introduces a new quantum number that describes what is different about the levels. • These quantum numbers then appear in the expression for the energies, in selection rules for transitions, and in the magnitudes of transition rates.

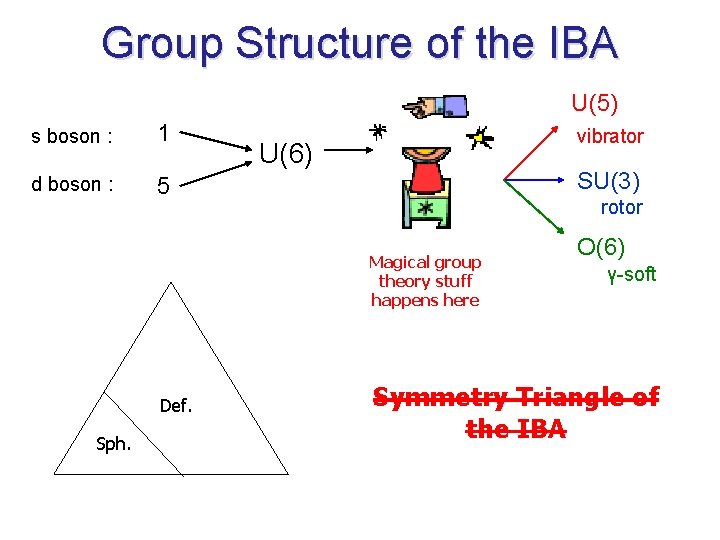
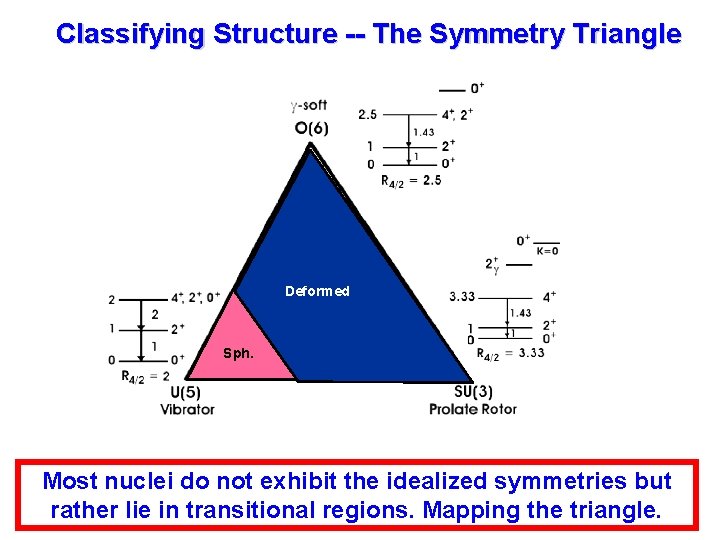
Group Structure of the IBA U(5) s boson : 1 d boson : 5 vibrator U(6) SU(3) rotor Magical group theory stuff happens here Def. Sph. O(6) γ-soft Symmetry Triangle of the IBA

IBA Hamiltonian Counts the number of d bosons out of N bosons, total. Conserves the of with d bosons. Gives in the The rest arenumber s-bosons: Es = 0 since weterms deal only Hamiltonian wherewith theexcitation energies. of configurations of 2 d + bosons depend on their total combined angular Excitation. Allows energies ONLY on thein number of dd d momentum. fordepend anharmonicities the phonon multiplets. bosons. E(0) = 0, E(1) = ε , E(2) = 2 ε. d Mixes d and s components of the wave functions Most general IBA Hamiltonian in terms with up to four boson operators (given N)

U(5) Spherical, vibrational nuclei

Simplest Possible IBA Hamiltonian – given by energies of the bosons with NO interactions = E of d bosons + E of s bosons Excitation energies so, set s = 0, and drop subscript d on d What is spectrum? Equally spaced levels defined by number of d bosons 3 6+, 2 4+, 2+, 0+ 1 2+ 0 0+ nd 4+, 3+, 2+, 0+ What J’s? M-scheme Look familiar? Same as quadrupole vibrator. U(5) also includes anharmonic spectra

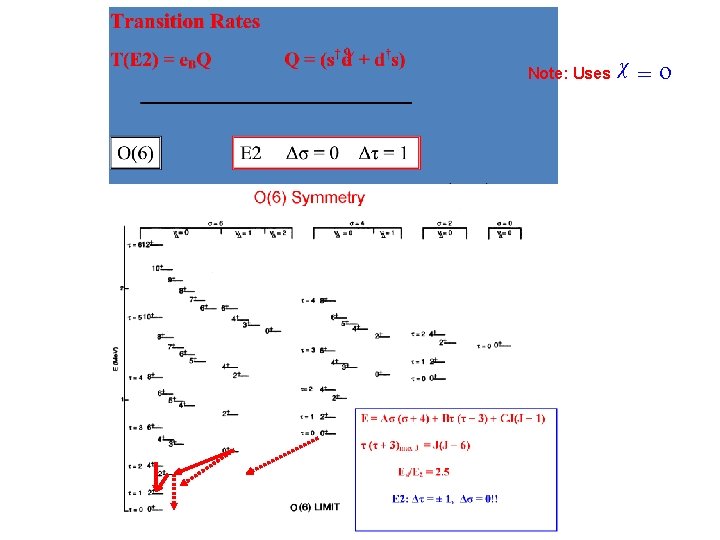
E 2 Transitions in the IBA Key to most tests Very sensitive to structure E 2 Operator: Creates or destroys an s or d boson or recouples two d bosons. Must conserve N T = e Q = e[s† + d†s + χ (d† )(2)] Specifies relative strength of this term

E 2 transitions in U(5) • χ = 0 so • T = e[s† + d†s] • Can create or destroy a single d boson, that is a single phonon. 3 6+, 4+, 3+, 2+, 0+ 2 4+, 2+, 0+ 1 2+ 0 0+ nd

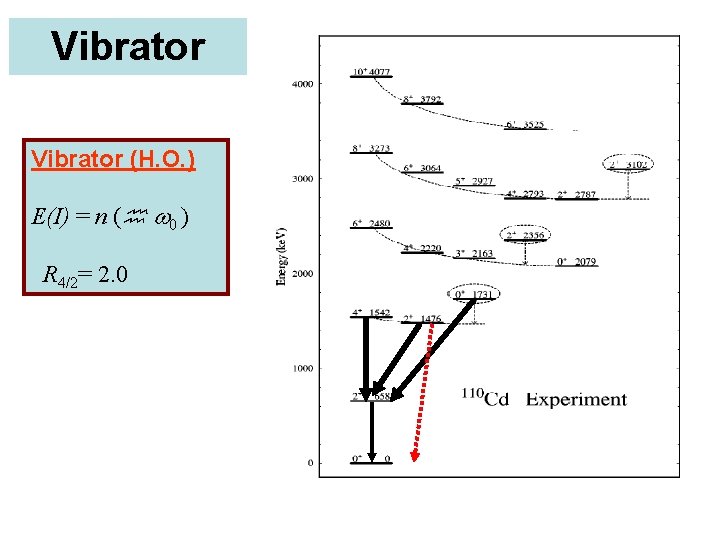
Vibrator (H. O. ) E(I) = n ( 0 ) 8+. . . R 4/2= 2. 0 6+. . . 2+ 0+

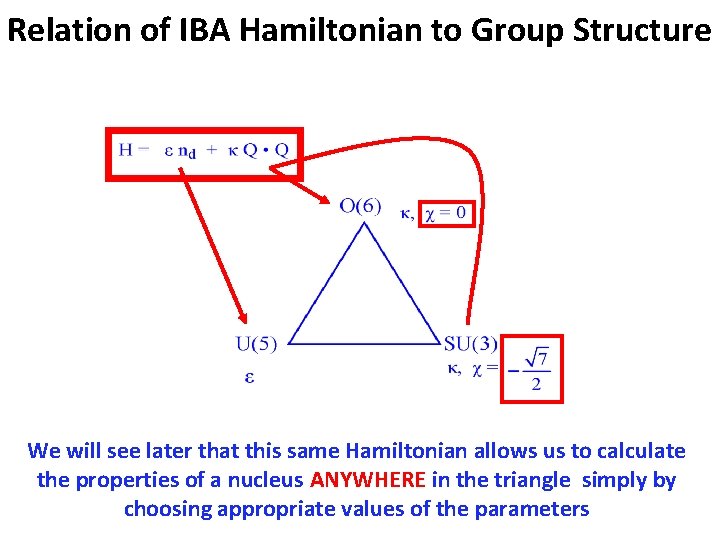
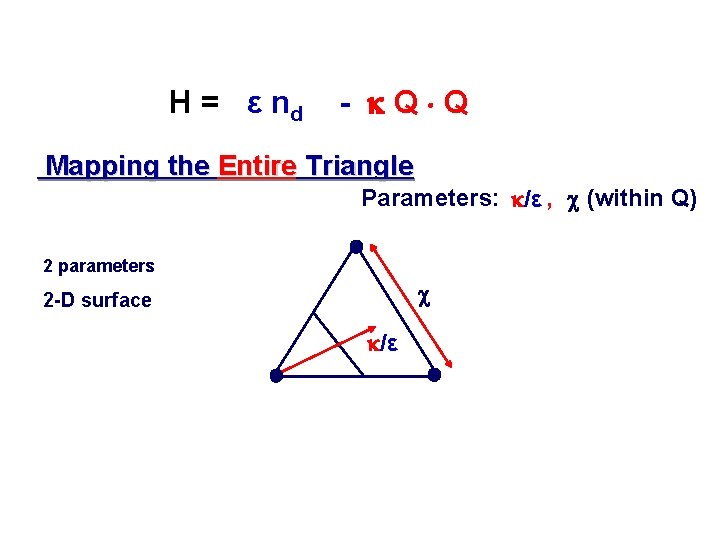
IBA Hamiltonian Complicated and not really necessary to use all these terms and all 6 parameters Simpler form with just two parameters – RE-GROUP TERMS ABOVE H = ε nd - Q Q Competition: ε nd Q Q Q = e[s† + d†s + χ (d† )(2)] term gives vibrator. term gives deformed nuclei. This is the form we will use from here on

Relation of IBA Hamiltonian to Group Structure We will see later that this same Hamiltonian allows us to calculate the properties of a nucleus ANYWHERE in the triangle simply by choosing appropriate values of the parameters

SU(3) Deformed nuclei

M

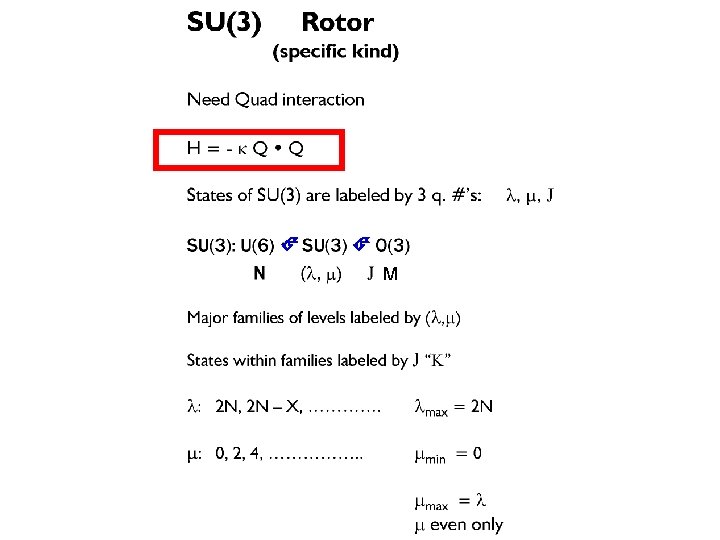
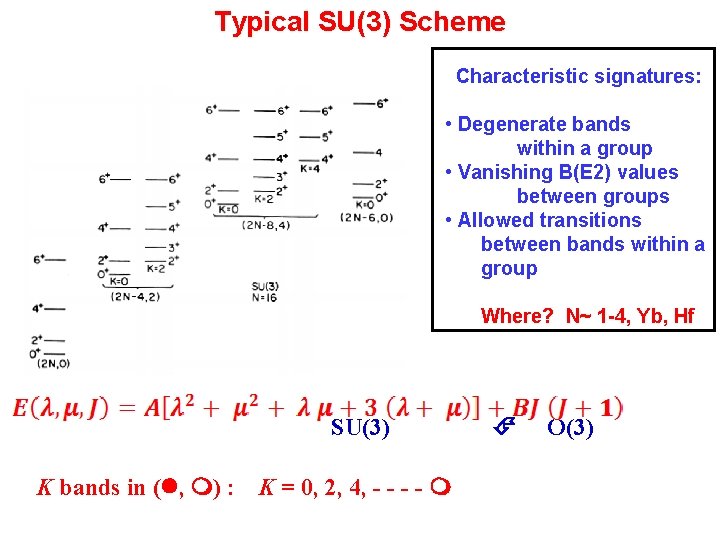
Typical SU(3) Scheme Characteristic signatures: • Degenerate bands within a group • Vanishing B(E 2) values between groups • Allowed transitions between bands within a group Where? N~ 1 -4, Yb, Hf SU(3) K bands in ( , ) : K = 0, 2, 4, - - O(3)

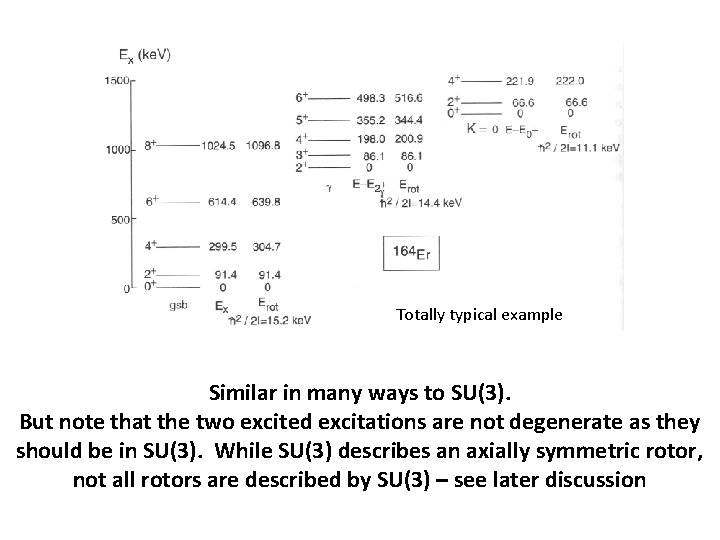
Totally typical example Similar in many ways to SU(3). But note that the two excited excitations are not degenerate as they should be in SU(3). While SU(3) describes an axially symmetric rotor, not all rotors are described by SU(3) – see later discussion


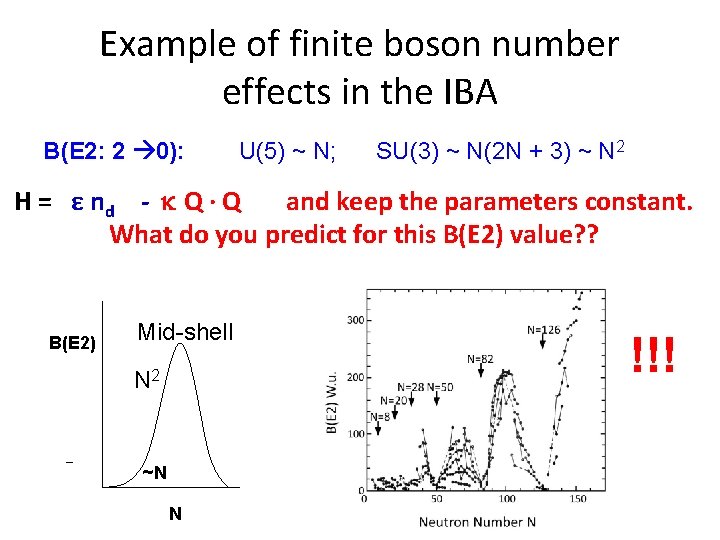
Example of finite boson number effects in the IBA B(E 2: 2 0): U(5) ~ N; SU(3) ~ N(2 N + 3) ~ N 2 H = ε nd - Q Q and keep the parameters constant. What do you predict for this B(E 2) value? ? B(E 2) Mid-shell N 2 ~N N !!!

O(6) Axially asymmetric nuclei (gamma-soft)



Note: Uses χ= o

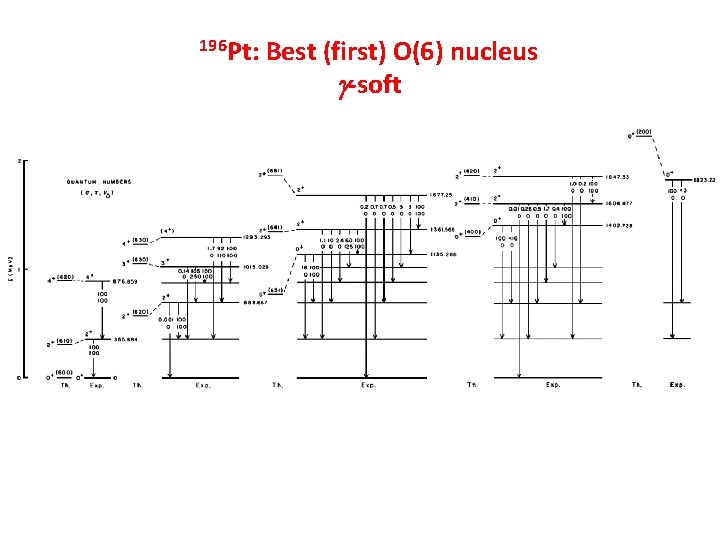
196 Pt: Best (first) O(6) nucleus -soft

Classifying Structure -- The Symmetry Triangle Deformed Sph. Most nuclei do not exhibit the idealized symmetries but rather lie in transitional regions. Mapping the triangle.

H = ε nd - Q Q Mapping the Entire Triangle Parameters: /ε , c (within Q) 2 parameters c 2 -D surface /ε

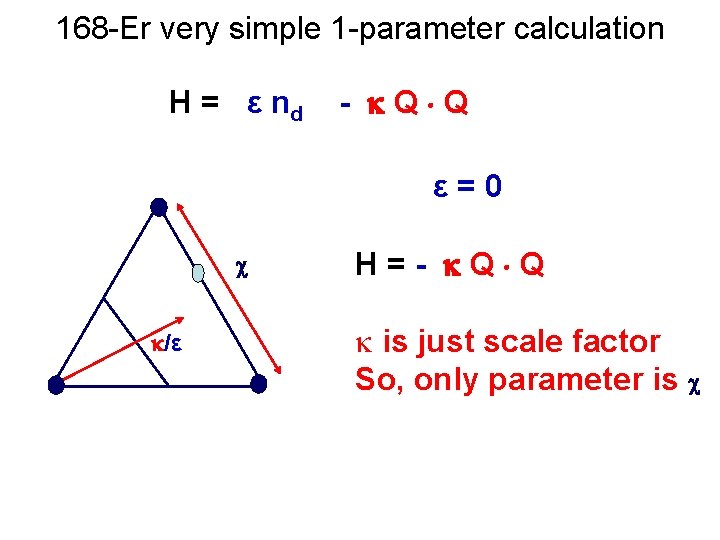
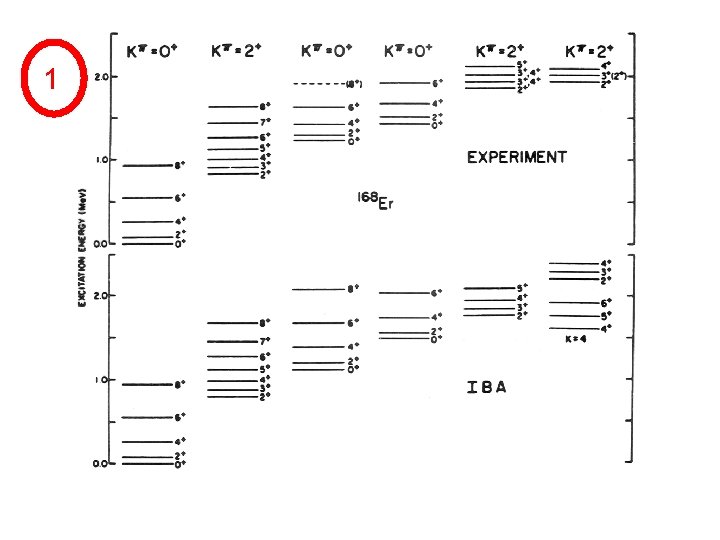
168 -Er very simple 1 -parameter calculation H = ε nd - Q Q ε=0 c /ε H = - Q Q k is just scale factor So, only parameter is c

1


2 “Universal” IBA Calculations for the SU(3) – O(6) leg H=-κQ • Q κ is just energy scale factor Ψ’s, B(E 2)’s independent of κ Results depend only on χ [ and, of course, vary with NB ] Can plot any observable as a set of contours vs. NB and χ.

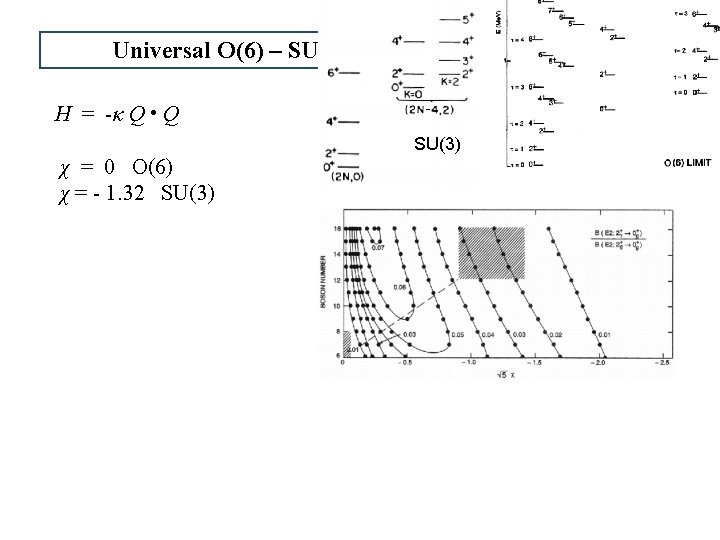
Universal O(6) – SU(3) Contour Plots H = -κ Q • Q SU(3) χ = 0 O(6) χ = - 1. 32 SU(3)



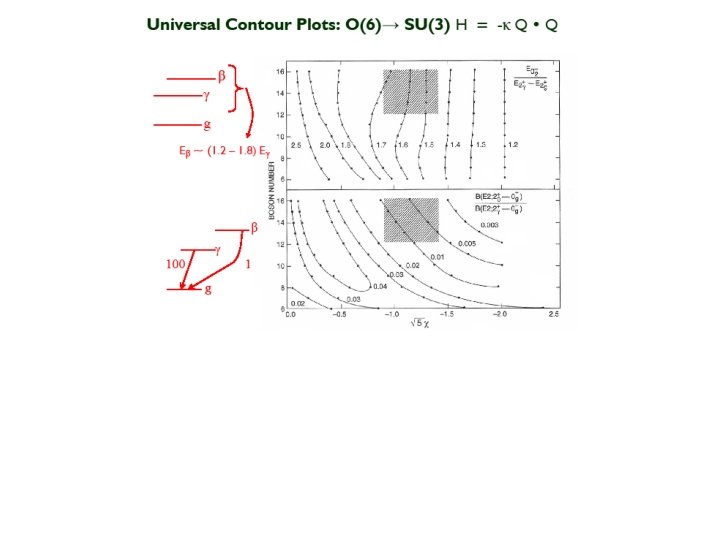
Mapping the entire triangle Technique of orthogonal crossing contours (OCC)

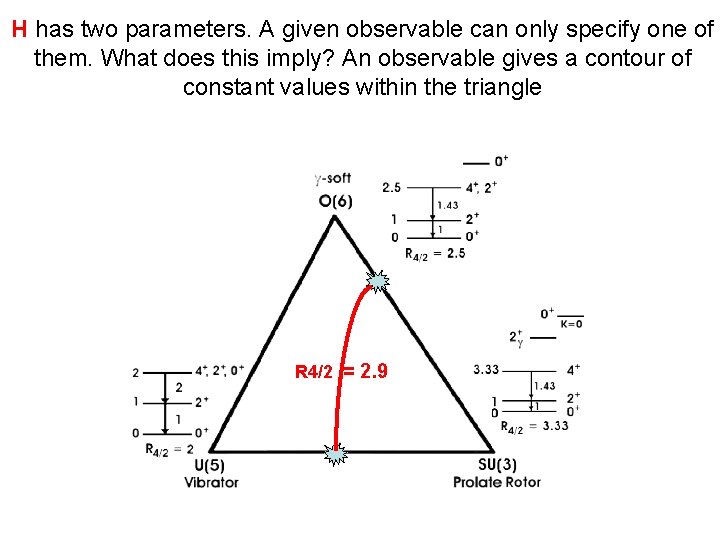
H has two parameters. A given observable can only specify one of them. What does this imply? An observable gives a contour of constant values within the triangle R 4/2 = 2. 9

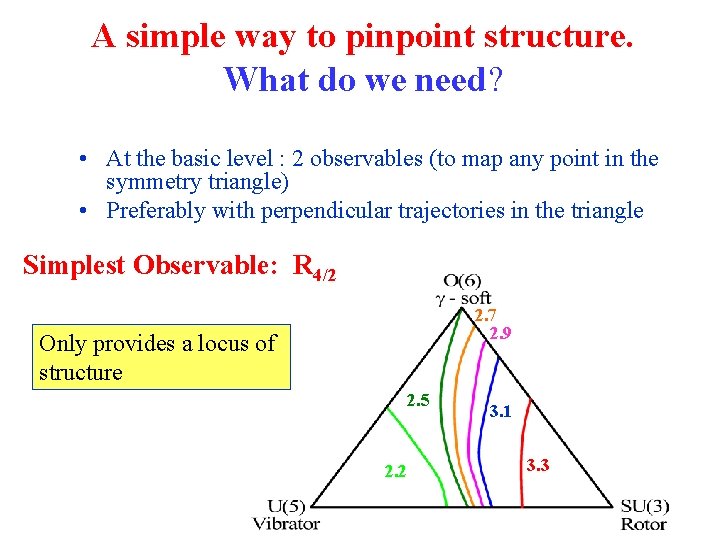
A simple way to pinpoint structure. What do we need? • At the basic level : 2 observables (to map any point in the symmetry triangle) • Preferably with perpendicular trajectories in the triangle Simplest Observable: R 4/2 2. 7 2. 9 Only provides a locus of structure 2. 5 2. 2 3. 1 3. 3

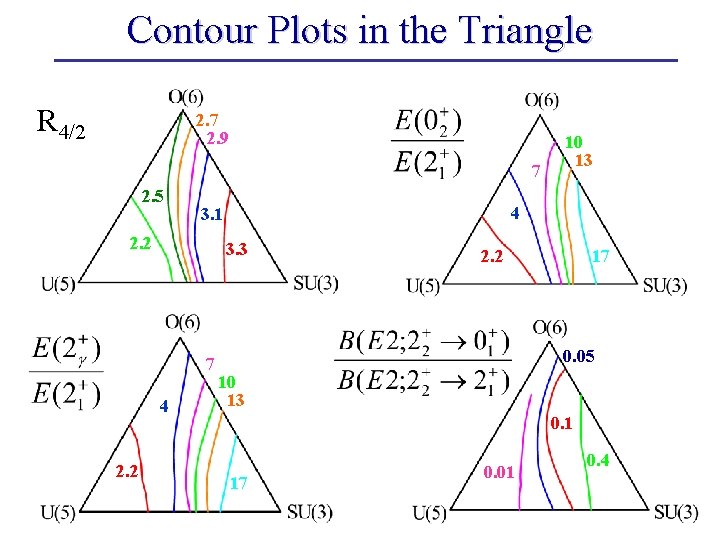
Contour Plots in the Triangle R 4/2 2. 7 2. 9 7 2. 5 3. 3 7 4 2. 2 4 3. 1 2. 2 10 13 2. 2 17 0. 05 10 13 0. 1 17 0. 01 0. 4

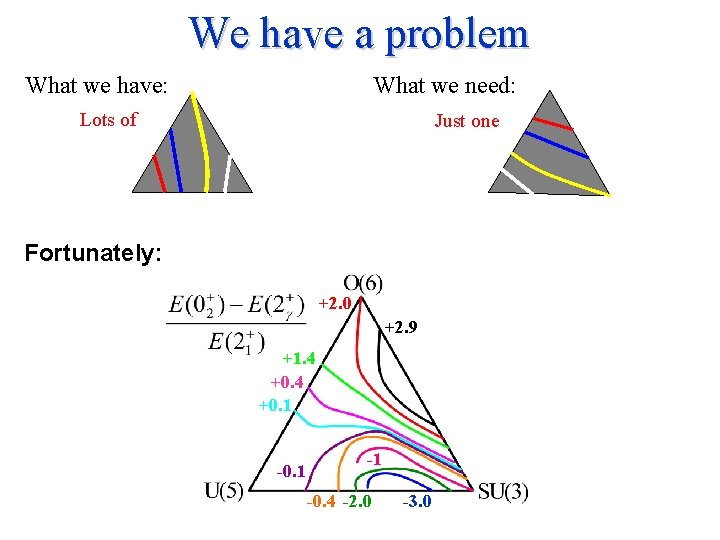
We have a problem What we need: What we have: Lots of Just one Fortunately: +2. 0 +2. 9 +1. 4 +0. 1 -0. 1 -1 -0. 4 -2. 0 -3. 0

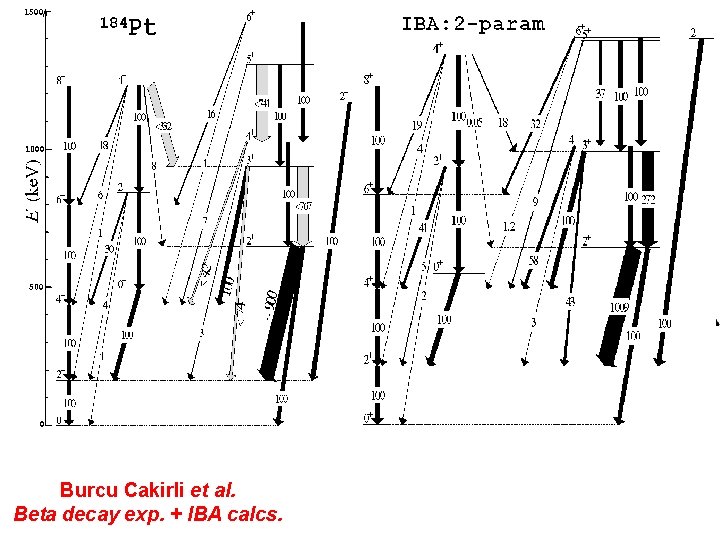
Mapping Structure with Simple Observables – Technique of Orthogonal Crossing Contours γ - soft Vibrator Burcu Cakirli et al. Beta decay exp. + IBA calcs. Rotor

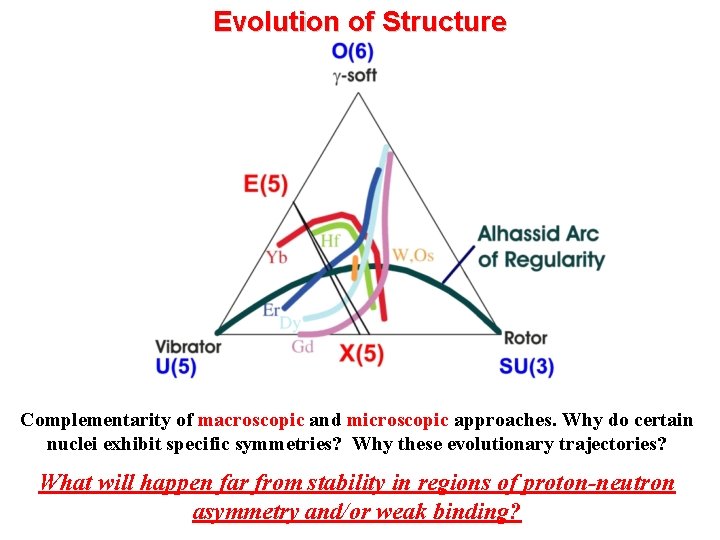
Evolution of Structure Complementarity of macroscopic and microscopic approaches. Why do certain nuclei exhibit specific symmetries? Why these evolutionary trajectories? What will happen far from stability in regions of proton-neutron asymmetry and/or weak binding?

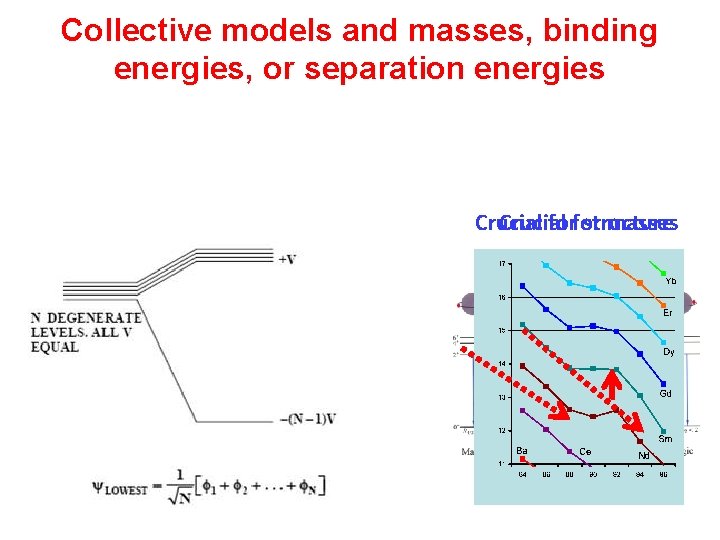
Collective models and masses, binding energies, or separation energies Crucial forfor structure masses

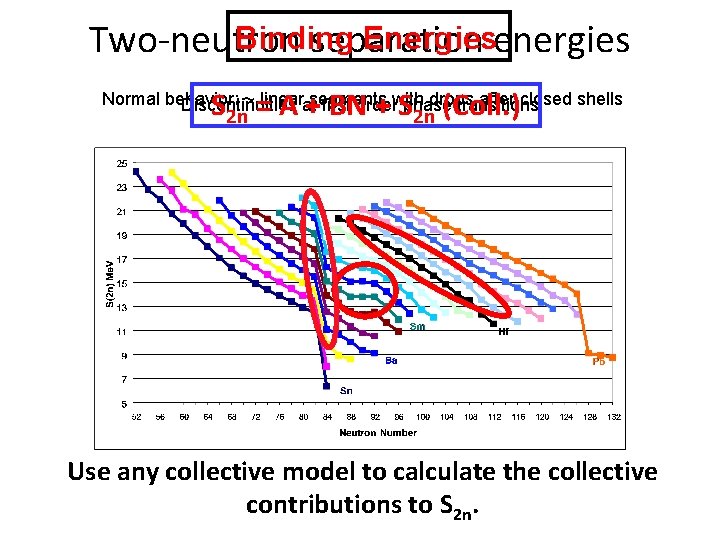
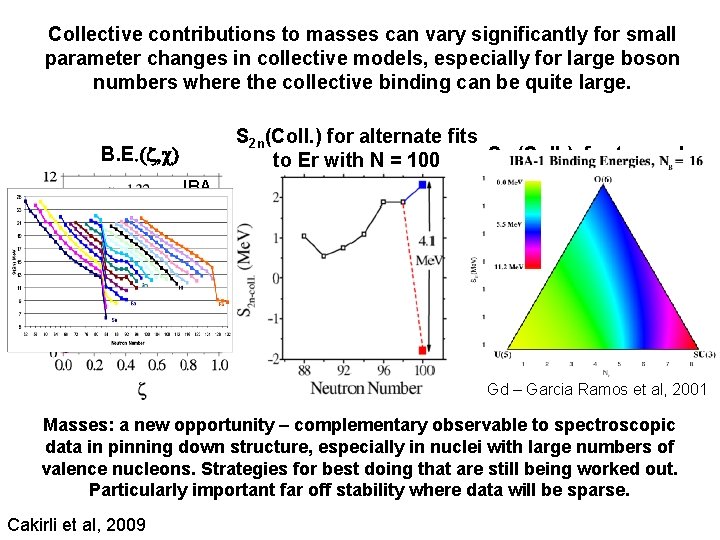
Binding Energiesenergies Two-neutron separation S 2 n = A + BN + S 2 n (Coll. ) Normal behavior: ~ linear segments with drops after closed shells Discontinuities at first order phase transitions Use any collective model to calculate the collective contributions to S 2 n.

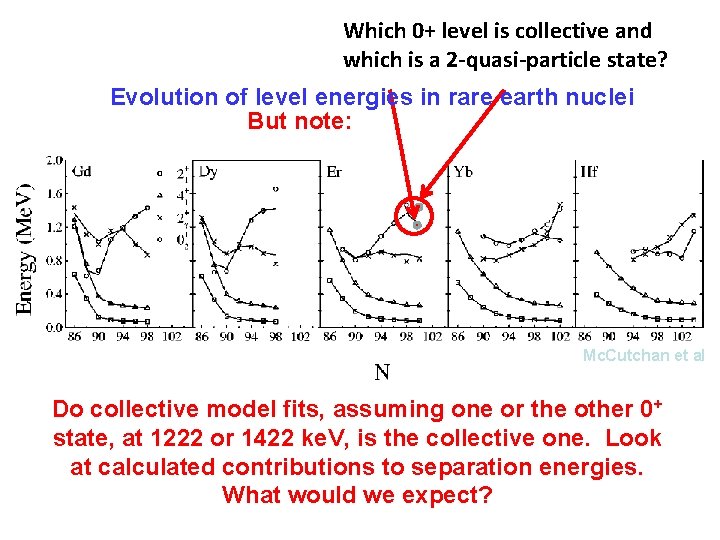
Which 0+ level is collective and which is a 2 -quasi-particle state? Evolution of level energies in rare earth nuclei But note: Mc. Cutchan et al Do collective model fits, assuming one or the other 0+ state, at 1222 or 1422 ke. V, is the collective one. Look at calculated contributions to separation energies. What would we expect?

Collective contributions to masses can vary significantly for small parameter changes in collective models, especially for large boson numbers where the collective binding can be quite large. S 2 n(Coll. ) for alternate fits S 2 n(Coll. ) for two calcs. to Er with N = 100 B. E. (z, c) B. E (Me. V) IBA Gd – Garcia Ramos et al, 2001 Masses: a new opportunity – complementary observable to spectroscopic data in pinning down structure, especially in nuclei with large numbers of valence nucleons. Strategies for best doing that are still being worked out. Particularly important far off stability where data will be sparse. Cakirli et al, 2009
 Shell cleanliness shell soundness shell texture shell shape
Shell cleanliness shell soundness shell texture shell shape Nnn egg
Nnn egg Short short short long long long short short short
Short short short long long long short short short Paulis exclusion principle
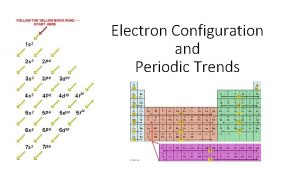
Paulis exclusion principle Pauli electron configuration
Pauli electron configuration Aufbau principle
Aufbau principle Electron distribution of oxygen
Electron distribution of oxygen Pauli exclusion principle examples
Pauli exclusion principle examples State pauli's exclusion principle class 11
State pauli's exclusion principle class 11 Orbital filling sequence and energy levels
Orbital filling sequence and energy levels Pauli exclusion principle
Pauli exclusion principle Pauli exclusion principle violation
Pauli exclusion principle violation As compared to long-range forecasts, short-range forecasts
As compared to long-range forecasts, short-range forecasts Contact force vs long range force
Contact force vs long range force Electrostatic force
Electrostatic force Shell long or short vowel
Shell long or short vowel Administrasi tes pauli
Administrasi tes pauli Makalah tes pauli
Makalah tes pauli Pauli leimio
Pauli leimio Contoh laporan tes pauli
Contoh laporan tes pauli Diagramas de orbitales
Diagramas de orbitales Gunter pauli
Gunter pauli Pauli blocking of light scattering in degenerate fermions
Pauli blocking of light scattering in degenerate fermions Pauli leimio
Pauli leimio Timo pauli
Timo pauli X=rsin
X=rsin Pauli crystals
Pauli crystals Klasikal adalh
Klasikal adalh Principe d exclusion de pauli
Principe d exclusion de pauli Domain and range review
Domain and range review Sigmet chart
Sigmet chart Short range communication
Short range communication Short range reference service
Short range reference service Tension contact or noncontact
Tension contact or noncontact What force provides centripetal force
What force provides centripetal force If you whirl a tin can on the end of a string
If you whirl a tin can on the end of a string The ratio of resistance force to effort force
The ratio of resistance force to effort force Force what is force
Force what is force Centrifugal forces in rwanda
Centrifugal forces in rwanda Non contact force
Non contact force Why electric force is conservative
Why electric force is conservative Centripetal force and gravitational force
Centripetal force and gravitational force Normal force and gravitational force
Normal force and gravitational force Normal force and shear force
Normal force and shear force Buoyant force and archimedes principle
Buoyant force and archimedes principle Archimedes principle states that
Archimedes principle states that Newton's first law
Newton's first law Chapter review motion part a vocabulary review answer key
Chapter review motion part a vocabulary review answer key Ap gov review final exam review
Ap gov review final exam review Narrative review vs systematic review
Narrative review vs systematic review Systematic review definition
Systematic review definition Narrative review vs systematic review
Narrative review vs systematic review Book review examples
Book review examples Short story test review
Short story test review Short book review for students
Short book review for students Maikling kwento
Maikling kwento Heterozygous short-hair x heterozygous short-hair
Heterozygous short-hair x heterozygous short-hair Us army battalion organization chart
Us army battalion organization chart Sales force structure method
Sales force structure method A4pa
A4pa Af chain of command
Af chain of command Ales force structure
Ales force structure Sales force organization structure
Sales force organization structure Enlisted force structure powerpoint
Enlisted force structure powerpoint What is meant by structure dependence
What is meant by structure dependence Structure of review writing
Structure of review writing Nail structures
Nail structures Cae writing guide
Cae writing guide Review structure
Review structure Structure of formal essay
Structure of formal essay Chapter 7 cell structure and function section review 7-2
Chapter 7 cell structure and function section review 7-2 Review sentence structure
Review sentence structure