The Pigeonhole Principle Pigeonhole principle The pigeonhole principle















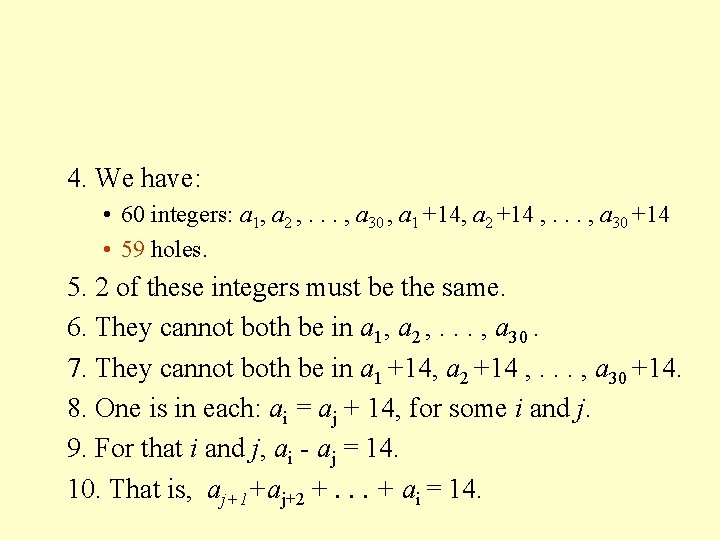
- Slides: 16

The Pigeonhole Principle

Pigeonhole principle The pigeonhole principle : If k is a positive integer and k+1 or more objects are placed into k boxes, then there is at least one box containing two or more of the objects. A common way to illustrate this principle is by assuming that k+1 pigeons fly to k pigeonholes. Then, there must be at least one pigeonhole containing at least two pigeons. The pigeonhole principle is a trivial observation, which however can be used to prove many results.

Example 1 In a room of 13 people, 2 or more people have their birthday in the same month. Proof: (by contradiction) 1. Assume the room has 13 people and no 2 people have their birthday in the same month. 2. There must be at least 13 different months. 3. Statement 2. is false, so the assumption is false.

The pigeonhole principle • Let m 1, m 2, … , mn be positive integers. • If m 1 + m 2 +. . . + mn - n + 1 objects are put into n boxes, • Then either • the 1 st box has at least m 1, or • the 2 nd box has at least m 2, or …, or • the nth box has at least mn objects.

Proof by Contradiction • Assume m 1 + m 2 +. . . + mn - n + 1 objects are put into n boxes, and • the 1 st box has at most m 1 - 1, and • the 2 nd box has at most m 2 - 1, and …, and • the nth box has at most mn - 1 objects. • Then, at most m 1 + m 2 +. . . + mn - n objects are in the boxes, a contradiction.

Another Form of Pigeonhole Principle If A is the average number of pigeons/hole, then some hole contains at least A pigeons and some hole contains at most A pigeons.

Intuition A A A Cannot have all holes contain less than the average. Cannot have all holes contain more than the average.

Proof of Alternate Principle By contradiction: 1. Assume A is the average number of pigeons/hole. 2. Assume every hole contains at most A - 1 pigeons or every hole contains at least A + 1 pigeons. 3. Let n denote the number of holes. 4. Assume every hole contains at most A - 1 pigeons. 5. All holes contain at most n( A - 1 ) < n. A pigeons, a contradiction.

5. Assume every hole contains at least A + 1 pigeons. 6. All holes contain at least n( A + 1) > n. A pigeons, a contradiction. 7. Therefore, some hole contains at least A pigeons and some hole contains at most A pigeons.

Applications of pigeonhole principle • If n + 1 pigeons are distributed among n holes, then some hole contains at least 2 pigeons. • If 2 n + 1 pigeons are distributed among n holes, then some hole contains at least 3 pigeons. • If kn + 1 pigeons are distributed among n holes, then some hole contains at least k + 1 pigeons. The average number of pigeons/hole = k + 1/n and k + 1/n = k + 1.

Applications. . . • In any group of 367 people, there must be at least 1 pair with the same birthday. • If 4 different pairs of socks are scrambled in the drawer, only 5 socks need to be selected to guarantee finding a matching pair. • In a group of 61 people, at least 6 were born in the same month.

Applications. . . • If 401 letters were delivered to 50 houses, then some house received at most 8 letters. • If x 1, x 2, …, x 8 are distinct integers, then some pair of these have the same remainder when divided by 7.

Applications. . . • Given a set of 7 distinct integers, there are 2 whose sum or difference is divisible by 10. • Set this up so that there are 6 pigeon holes. • Partitioning the integers into equivalence classes according to their remainder when divided by 10 yields too many classes. • Consider: • {[0]}, {[1], [9]}, {[2], [8]}, {[3], [7]}, {[4], [6]}, {[5]}. • If 2 integers are in the same set either their difference is divisible by 10 or their sum is divisible by 10.

Applications. . . • Suppose • 50 chairs are arranged in a rectangular array of 5 rows and 10 columns. • 41 students are seated randomly in the chairs (1 student/chair). • Then, • • some row contains at least 9 students some row contains at most 8 students some column contains at least 5 students some column contains at most 4 students.

Applications. . . • A patient has 45 pills, with instructions to take at least 1 pill/day for 30 days. • Prove: there is a period of consecutive days in which the patient takes a total of 14 pills. 1. Let ai be the number of pills taken through the end of the ith day. 2. 1 a 1 < a 2 <. . . < a 30 45. 3. a 1 + 14 < a 2 + 14 <. . . < a 30 + 14 45 + 14 = 59
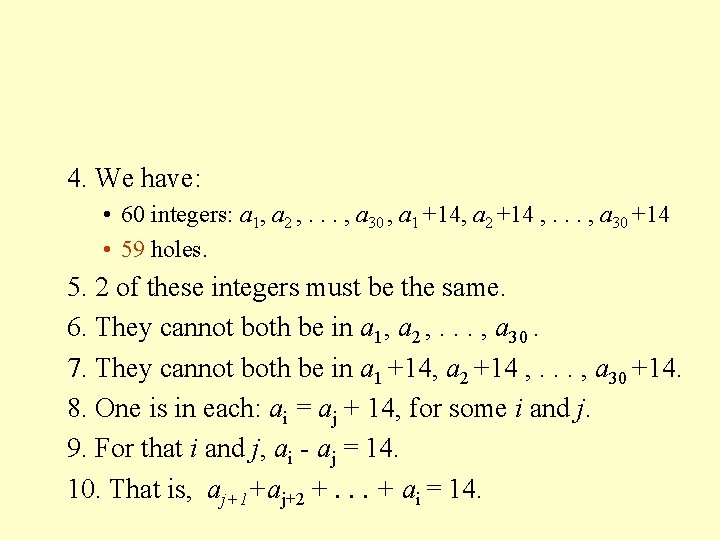
4. We have: • 60 integers: a 1, a 2 , . . . , a 30 , a 1 +14, a 2 +14 , . . . , a 30 +14 • 59 holes. 5. 2 of these integers must be the same. 6. They cannot both be in a 1, a 2 , . . . , a 30. 7. They cannot both be in a 1 +14, a 2 +14 , . . . , a 30 +14. 8. One is in each: ai = aj + 14, for some i and j. 9. For that i and j, ai - aj = 14. 10. That is, aj+1+aj+2 +. . . + ai = 14.
 Pigeonhole principle
Pigeonhole principle Dirichlet's box principle
Dirichlet's box principle Pigeonhole principle
Pigeonhole principle Pigeonhole principle exercises
Pigeonhole principle exercises Pumping lemma pigeonhole principle
Pumping lemma pigeonhole principle State the pigeonhole principle
State the pigeonhole principle Pigeonhole principle
Pigeonhole principle Pigeonhole principle in discrete mathematics
Pigeonhole principle in discrete mathematics Pigeonhole principle example
Pigeonhole principle example Pigeon hole theory
Pigeon hole theory State the pigeonhole principle
State the pigeonhole principle Application of pigeonhole principle
Application of pigeonhole principle Magnetrejects
Magnetrejects Pigeon hole algorithm
Pigeon hole algorithm Pigeonhole
Pigeonhole Lời thề hippocrates
Lời thề hippocrates Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể