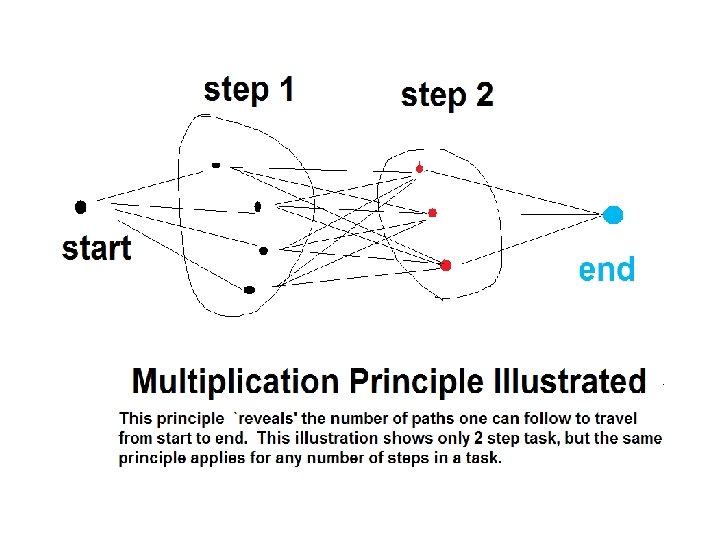
Multiplication Principle and Addition Principle 1 Multiplication Principle

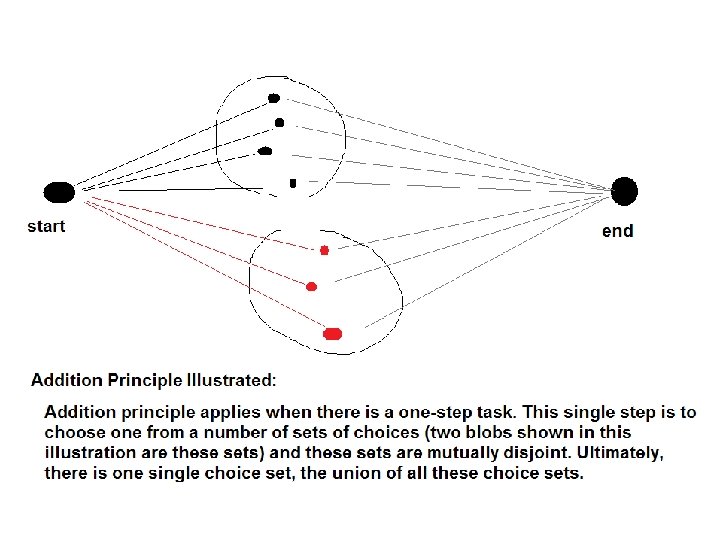
Multiplication Principle and Addition Principle 1. Multiplication Principle: Suppose a task is accomplished by n steps and each step requires a choice from a number of available choices. Let these numbers be A 1, A 2, . . . An 2. Then, the total number of ways to accomplish this task is 3. A 1 x A 2 x A 3 x. . An. 2. Addition Principle: Suppose a task is accomplished by choosing an object from the union of disjoint sets with cardinalities B 1, B 2, B 3, . . . Bn. Then, the total number of ways to accomplish this task is B 1+ B 2+ B 3 +. . . Bn.

Set Theoretic Descriptions of the two principles • The cardinality of the Cartesian product of n sets A 1, A 2, . . An is given by n (A 1 x A 2 x. . . An) = n(A 1). n(A 2). . . n(An). • The cardinality of the disjoint union of n sets B 1, B 2, . . Bn is given by n (B 1 U B 2 U. . . Bn)= n(B 1) + n(B 2)+. . . + n(Bn)

Examples • On a table, there is a pile of 10 apples and another pile of 15 pears. 1. How many choices do you have if you are instructed to pick an apple and a pear? 2. How many choices do you have if you are instructed to pick an apple or a pear?

Mistakes you must avoid • Suppose there are 4 doctors and 5 chess players in a room with 7 people. If you are instructed to pick a doctor or a chess player in this room (and slap the face) how many choices do you have? Is your answer 4+5 = 9 ? Then, review your knowledge of addition principle.

Read the problems carefully. In a room, there are 7 people. Everyone in that room is either a chess player or a doctor. 4 of them are doctors and 5 of them are chess players. In how many ways can one accomplish each of the following tasks? 1. Task is to get into the room, pick a chess player and play a chess with. Then, pick a doctor and ask for an opinion about your asthma symptom. 2. Task is to pick a team of two people, consisting of one chess player and one doctor.

• Addition Principle is frequently applied in a form of `subtraction’ principle. n(A B) = n(A) – n(B) Example: In a basket of 30 Easter eggs, there are 7 green eggs. Your task is to pick an egg that is not green. How many choices do you have? The answer: 30 -7= 23. 23 choices. Another Example: (See the Venn diagram of chess players and doctors. ) We will approach the second question in the previous slide in the following way. Initially, we write a name of a chess player and (next to it) write a name of a doctor. Consider this writing as a tentative list of 2 -team members. There are 5 x 4=20 possible ways of writing a pair of names in this way. But, exactly 2 of them are a pair of names of a same person (which is not permitted). So, the answer to the second question ( of forming a team of chess_player-doctor pair) is 20 -2=18.

Multiplication Principle is frequently applied in the form of Division Principle. • Division Principle: If A=B x C (cartesion product of B and C), then n(B) = n(A) / n(C). EXAMPLE 1: Gregor Samsa goes to walk every morning wearing a hat and carrying a cane. He has 2 hats, which are identical except that one is grey and the other is brown. He has 3 canes. He is color blind. In how many ways, can he choose a hat and a cane to go out for a walk based on his discerning ability? Answer: If he were able to tell brown from grey, there would be 2 x 3= 6 ways. But, now that all the hats are identical to him from his view, there are 6 / 2 = 3 ways.

Division Principle re-stated: Suppose a task A consists of accomplishing a task B followed by a task C. Then, the number of ways to accomplish task B is given by the number of ways to accomplish the task A divided by the number of ways to accomplish task C. EXAMPLE 2. How many different words can be formed by rearranging the letters in the word “ELEMENT”? Answer: 7! / 3! ( Explain. . . )

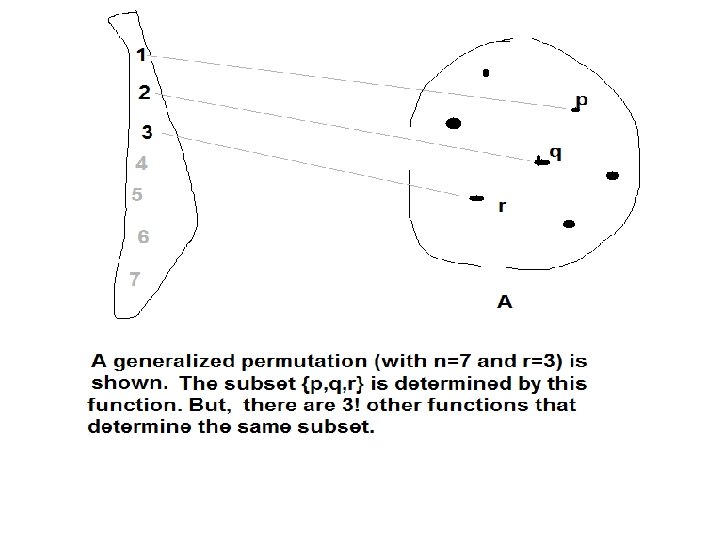
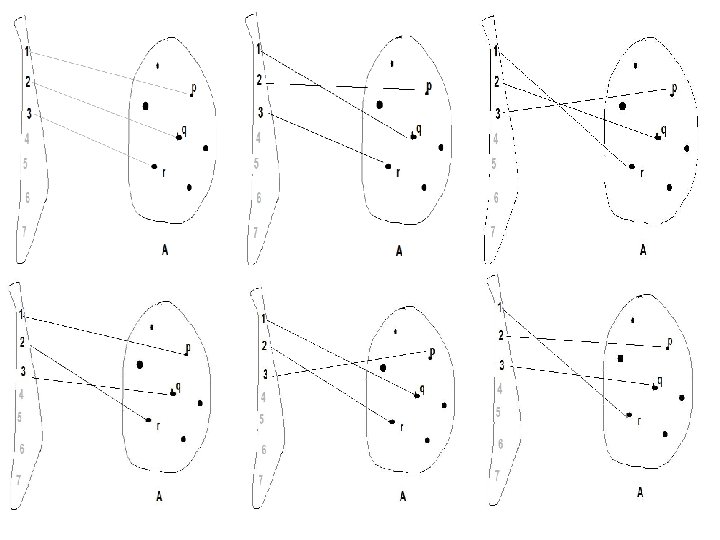
Permutation • Informally, a permutation on a set of n elements is an ordering of these elements. • Formally, a permutation on a set of n elements is a one-to-one correspondence between the set and itself. • Number of permutations on a set of n elements • Generalized Permutation: Let A be a set of n elements and r< n. Any one-to-one function from the set {1, 2, 3, . . r} into the set A is called a generalized permutation of the k elements on the set A. • Number of generalized permutation of r elements on the set of n elements is denoted by n. Pr. • n. P r x (n-r)! = n! by multiplication principle.

Combination • Let r<n. An r-combination on the set of n elements is a subset with cardinality r. • n. Cr denotes the number of all the rcombinations on the set of n elements. • n. Pr and n. Cr are related by the following equation n. Pr = n. Cr x r! (illustrated below)

• Picking a generalized permutation, a one-to-one function from {1, 2, . . r} into The set A of n elements is equivalent to STEP 1: Picking a subset of A that has r elements. STEP 2: Picking a permutation on these r elements. Therefore, n. Pr= n. Cr x r!

Summary • n! = number of permutations on n objects. • n. Pr = number of r-permutations on n objects = • n. Cr = number of r-sets that can be formed from n objects =n Pr / r! =

Partition • Let A be a set of n elements. If, for some subsets A 1, A 2, . . . , Ak that are pairwise disjoint, A= A 1 U A 2 U. . . U Ak then we say {A 1, A 2, . . . Ak} is a partition of A.

Ordered Partition • Let a 1+a 2+. . . ak= n and a 1< a 2<. . ak ( < here means less than or equal to) The sequence of subsets A 1, A 2, . . Ak with cardinalities a 1, a 2, . . . ak is called an ordered partition if these sets are mutually disjoint and their union is the set A.

Number of ordered partitions • • How many ordered partitions of a given type does a set of n element have? Experiment: Consider a set of 7 elements. How many ordered partitions of type (2, 2, 3) are there? The construction of a partition of a given type can be considered as a multi-step task. The number of these steps is 1 less than the number of subsets that form the partition. In this particular experiment, 2 steps. STEP 1: Pick a subset of 2 elements (from 7 elements) STEP 2: Pick a subset of 2 elements (from the remaining 5 elements) Now, we employ the multiplication principle: 7 C 2 x 5 C 2 =

Counting Ordered Partitions of a Given Type Let a 1+a 2+. . . ak = n. The number of type (a 1, a 2, . . ak) partitions of a set of n elements is given by

Application (of partition counting) • How many different words can be formed by rearranging the letters in the word “ MISSISSIPI” ? Discussion: Compare this problem with the following problem: `` How many ordered partitions of the type (1, 1, 4, 4) are there for a set of 10 elements? ”. How are these two problems related?

• Given a 10 element set, imagine these elements are doors along a hall way of a hotel. Imagine your duty is to write letter M on 1 door letter P on 1 door letter S on 4 doors letter I on 4 doors This job is equivalent to forming a word by an arrangement of letters in “MISSISSIPI”. This job is also equivalent to forming a type (1, 1, 4, 4) ordered partition of the 10 element set.