Properties of Matter Heat and Thermodynamics Dr Mohamed

Properties of Matter Heat and Thermodynamics Dr. / Mohamed Abdel-Rahman El-Sayed Head of Nuclear Engineering department

CONTENTS Part (1) Properties of Matter § Chapter (1) : Units and Dimensions § Chapter (2) : Elastic Properties of Matter § Chapter (3) : Fluid mechanics Part (2) Heat and Thermodynamics § Chapter (4): Heat § Chapter (5): Thermodynamics

Chapter 1 Units and Dimensions

1 Units of Physical quantities • The study of properties of matter or any other branch in physics starts by defining a number of fundamental physical quantities as length, math and time and the unit of measuring each of them. • Many other quantities called derived quantities can be expressed in terms of these fundamental quantities, as velocity, pressure and force. Systems of units: The units of the fundamental quantities mass, length and time in the three systems of units are: French System : gm – cm – second. International System (SI): kg – meter – second. British System : Pound – foot – second. In this book we use only the international system of units of the three fundamental quantities.

Remarks It was found that it is necessary to introduce other fundamental quantities as: • Absolute temperature in Kelvin • Electric current intensity in Ampere • Quantity of matter in mole • Luminous intensity in Candela Relation between different systems is important in some engineering applications to change the unit of a quantity into another unit.

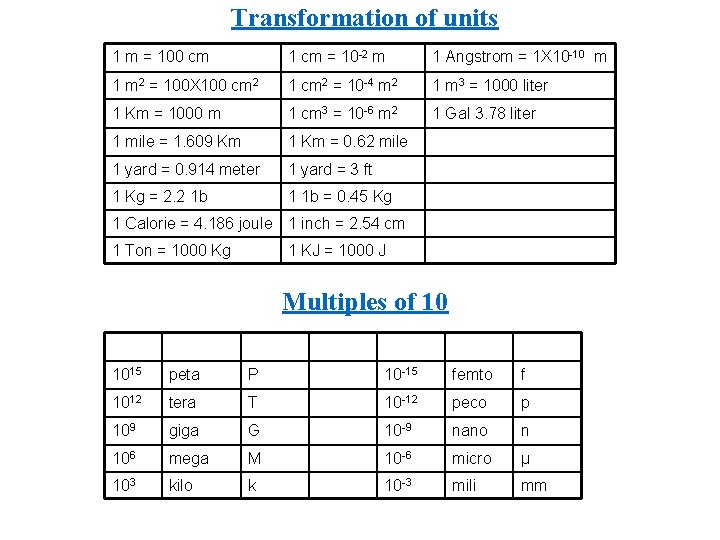
Transformation of units 1 m = 100 cm 1 cm = 10 -2 m 1 Angstrom = 1Χ 10 -10 m 1 m 2 = 100Χ 100 cm 2 1 cm 2 = 10 -4 m 2 1 m 3 = 1000 liter 1 Km = 1000 m 1 cm 3 = 10 -6 m 2 1 Gal 3. 78 liter 1 mile = 1. 609 Km 1 Km = 0. 62 mile 1 yard = 0. 914 meter 1 yard = 3 ft 1 Kg = 2. 2 1 b 1 1 b = 0. 45 Kg 1 Calorie = 4. 186 joule 1 inch = 2. 54 cm 1 Ton = 1000 Kg 1 KJ = 1000 J Multiples of 10 1015 peta P 10 -15 femto f 1012 tera T 10 -12 peco p 109 giga G 10 -9 nano n 106 mega M 10 -6 micro μ 103 kilo k 10 -3 mili mm

Dimensions: Dimensional formula is a method to express a derived quantity in terms of the fundamental quantities whose dimensions are: Mass : M Length : L Time : T The dimension of a derived quantity can be in general written in the form: M x. L y. T z The power of M, L and T depends on the definition of the physical quantity. Example: What is the dimensional formula of the following derived quantities: area – density – velocity – acceleration – force – momentum – work - kinetic energy - potential energy - power and pressure

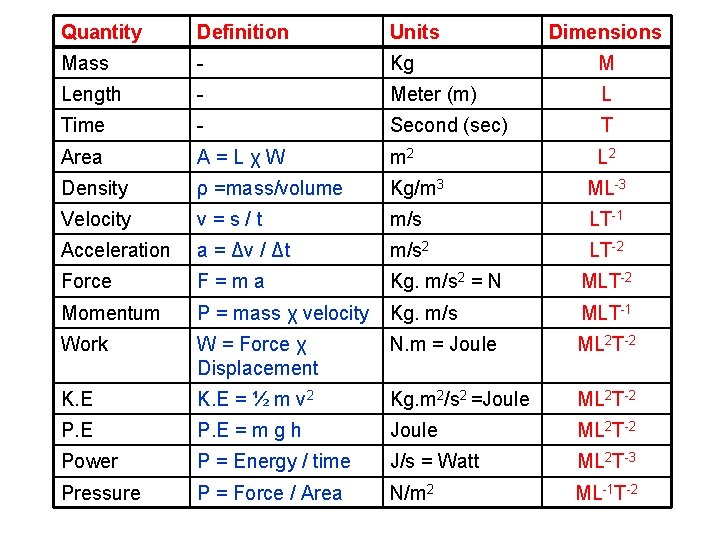
Quantity Definition Units Dimensions Mass - Kg M Length - Meter (m) L Time - Second (sec) T Area A=LχW m 2 L 2 Density ρ =mass/volume Kg/m 3 ML-3 Velocity v=s/t m/s LT-1 Acceleration a = Δv / Δt m/s 2 LT-2 Force F=ma Kg. m/s 2 = N MLT-2 Momentum P = mass χ velocity Kg. m/s MLT-1 Work W = Force χ Displacement N. m = Joule ML 2 T-2 K. E = ½ m v 2 Kg. m 2/s 2 =Joule ML 2 T-2 P. E = m g h Joule ML 2 T-2 Power P = Energy / time J/s = Watt ML 2 T-3 Pressure P = Force / Area N/m 2 ML-1 T-2

Use of the dimensional formula 1 - To check the equation The units and hence the dimensions of each term of the two sides of the equation must be the same. Otherwise the equation is not correct. Example: Show that the equation describing the change of the velocity of transverse wave v in a string stretched by a tension force T is given by: Where μ is the mass of the string per unit length The dimensions of the LHS: LT-1 The dimensions of the RHS: (MLT-2/ML-1 )1/2 = (L 2 T-2)1/2 = LT-1 The equation is correct since the two sides have the same dimensions.

Use of the dimensional formula 2 - To find new relation containing 3 variables: The dimensions of any physical quantity can be written in the form of : Mx. Ly. Tz The powers x, y and z can be obtained by equating the powers of M, L and T of the quantity in the left side and those in the right side , then solving the three equations. Example: The time T of one vibration of the simple pendulum depends on : (a) the mass of sphere attached to its end (m) (b) the length of the string (L) (c) the acceleration of the gravity (g)

It is seen that: • The mass of the sphere doesn't affect the time of one vibration. • The period is directly proportional to the square root of the length of the pendulum. • The acceleration of gravity on the earth's surface is nearly constant. At the moon's surface the period is longer than on earth since the gravity is only 1/6 that on earth.

Chapter 2 Elastic Properties of Matter

1 - Introduction • An object is deformed when a contact force is applied on it. A deformation is a change in the size or shape of the object. • When the contact forces are removed, an elastic object returns to its original shape and size. Many objects are elastic as long as the deforming forces are not too large. • Any object may be permanently deformed or even broken if the acting forces are too large. • Elasticity is the ability of the body to maintain its original shape and dimensions after removing the external force acting on it. 2 - Hooks law for Tensile and compressive forces: For an object of initial length (L) subjected to a tensile or compressive force of magnitude “F”, the length changes by an amount “ΔL”. Hooks law states that “the deformation is proportional to the deforming forces as long as they are not too large” where K is a constant, called the spring constant.

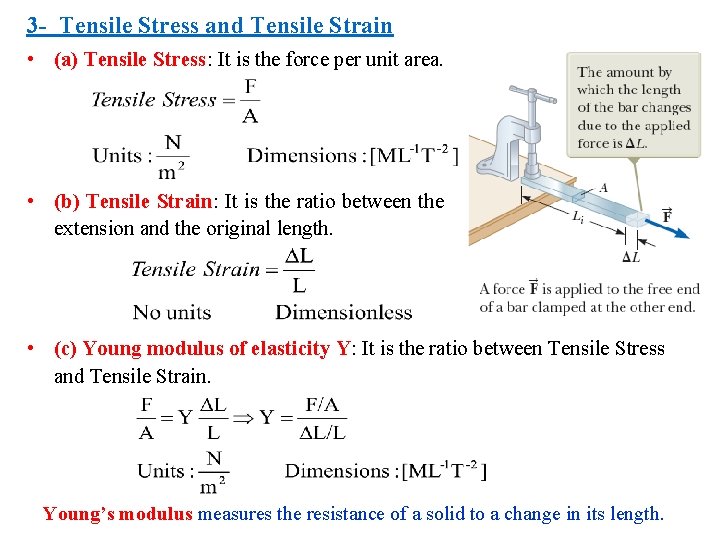
3 - Tensile Stress and Tensile Strain • (a) Tensile Stress: It is the force per unit area. • (b) Tensile Strain: It is the ratio between the extension and the original length. • (c) Young modulus of elasticity Y: It is the ratio between Tensile Stress and Tensile Strain. Young’s modulus measures the resistance of a solid to a change in its length.

Example: A man whose weight is 0. 8 KN is standing upright. By how much is his femur shortened compared to when he is lying ? Assume that the compressive force on each femur is half his weight. The average cross-sectional area of the femur is 8 cm 2 and its length when lying down is 43 cm. Young modulus for a femur is 9. 4× 109 Pa.

4 - Stress – Strain Curve (I) Ductile Material: When a load is attached to one end of a thin long wire its length increases according to the following graph: (1) Proportional limit: For small loads, the stress is directly proportional to the strain tell the proportional limit. (2) Elastic limit: The solid returns to its original length when the stress is removed as long as the stress doesn't exceed the elastic limit. If the stress exceeds the elastic limit, the material is permanently deformed. (3) Ultimate strength: Maximum stress that can be withstood without breaking. (4) Breaking point: Examples of ductile materials are soft metals such as gold, silver and copper.

(II) Brittle Materials: The ultimate strength and the breaking point are close to each other. Examples: Bone, glass and ceramics.

5 - Shear and volume deformations (I) Shear deformation: Shear deformation is the result of a pair of equal and opposite forces that act parallel to two opposite surfaces. The Shear Strain is proportional to the Shear Stress as long as the stress is not too large. The constant of proportionality is the shear modulus S.

(II) Volume deformation – Bulk modulus: A solid immersed in a fluid (gas or liquid) is subjected to compression. The fluid pressure P is the force per unit area which is the volume stress. The volume of the solid “V” is compressed and decreases by an amount ΔV (final volume < initial volume) so ΔV is negative. The volume strain is proportional to the volume stress (as long as the stress is not too large) and the constant of proportionality is called the bulk modulus (B). where ΔP… change in pressure from the atmospheric pressure. The negative sign allows “B” to be positive, since ΔV is negative.

(II) Volume deformation – Bulk modulus: it is the ratio between the change in pressure and the relative change in volume. Bulk modulus measures the resistance of solids or liquids to changes in their volume. The negative sign means that the volume decreases as the pressure increases. In solids the value of bulk modulus is very large, which means that the change in volume requires very high pressure. In liquids the bulk modulus is also so large such that the liquid is said to be incompressible. In gases the value of B is relatively small. It is easy to change the volume of gas, since the intermolecular force between gas molecules is weak and the intermolecular spaces are wide.

Chapter 3 Fluid mechanics

1 - states of matter • Ordinary matter is classified into three states (phases): solids, liquids and gases. • We mean by fluid, liquid or gas, the substance that flows and has no definite shape. Fluid takes the shape of the container. • The streamline flow of fluids of no viscosity in a tube from one section to another satisfies two equations: Continuity equation and Bernoulli's equation. 2 - Pressure: Average pressure where F…magnitude of the force acting perpendicularly to a surface (N) A…. Surface area (m 2) Units of P (N/m 2) or Pascal (Pa) 1 atm = 1. 013× 105 Pa

Example: A woman weighting 534 N. find the average pressure due to its weight on the floor when (i) she wears tennis shoes of area 60 cm 2. (ii) she wears spike-heeled shoes of area 1 cm 2.

1 - Pascal's Principle “ A change in pressure at any point in a confined fluid is transmitted everywhere throughout the fluid ”. Hydraulic Lift The pressure increase ΔP due to the force F 1 on the small piston of area A 1 is : This increase in pressure is transmitted everywhere in the liquid, then So, if A 2=10 A 1 (10 times larger), then F 2=10 F 1 Since the volume of liquid displaced by each piston is the same, so The work done by moving the small piston = the work done by the large piston.

Example: In a hydraulic lift, if the radius of the small piston is 2 cm, and the radius of the large piston is 20 cm. (a) What weight can the large piston support when a force of 250 N is applied to the smaller piston ? (b) If the small piston moves 50 cm. what is the distance moved by the large piston ?

4 - The effect of gravity on fluid pressure § The pressure variation in a static fluid is : where point 2 is a depth “d” below point 1 in a liquid at rest in a vessel. § The pressure “ P ” at a depth “ d ” below the surface of a liquid open to the atmosphere is : where Patm …. . is the atmospheric pressure. ρ…. . Density of the fluid (ρ = mass/volume)

Example: A diver swims to a depth of 3. 2 m in water ( density = 1000 Kg/m 3 ). What is the increase in the force pushing in on her eardrum compared to what it was at the lake surface ? Area of the eardrum is 0. 6 cm 2.

5 - Archimedes Principle § When an object is immersed in a fluid, the pressure on the lower surface of the object is higher than the pressure on the upper surface. This difference in pressure leads to an upward force acting on the object, called the Buoyant force. Archimedes Principle: § “ A fluid exerts an upward buoyant force on a submerged object equal in magnitude to the weight of the volume of fluid displaced by the object. ” where Vsub …. . volume of the submerged part of the object. ρ…. . density of the fluid (ρ = mass/volume)

Example: What percentage of a floating icebergs volume is above the water ? The density of ice is 917 Kg/m 3 while the density of sea water is 1025 Kg/m 3 § At equilibrium, the weight of the iceberg equals the buoyant force. So, 89. 5 % of the ice is below the surface of water and 10. 5 % is above the surface.

6 - The Continuity Equation § The volume of liquid entering the tube equals the volume of liquid leaving it. The rate of flow is the volume passing per second. § The quantity of liquid flowing per second equals the product of area of the section and the velocity at this section. According to the continuity equation: for incompressible fluid, The velocity of liquid is inversely proportional to the area. where Av is the volume flow rate (m 3/s). So, the volume flow rate is constant (the volume of liquid in = the volume of liquid out)

7 - Bernoulli's Equation § It is one form of the conservation of energy which in general states that : “ Energy is neither created nor destroyed but can be transformed into other forms “. § The Bernoulli equation, which applied for non-viscous and incompressible streamline flow, states that : “ The sum of the pressure, Kinetic and Potential energy per unit volume is constant “. P ……. pressure (Pa) ρ ……. fluid density (Kg/m 3) y ……. height above a reference level (m) v ……. fluid speed (m/sec)

8 - Applications of Bernoulli's Equation (A)- Horizontal Pipe: (B)- Pressure at depth y below the surface: 1 y reference 2

(C)- Torricelli's theorem: Applying the Bernoulli's equation at point “ 1” and “ 2”. 1 y 2 v 2

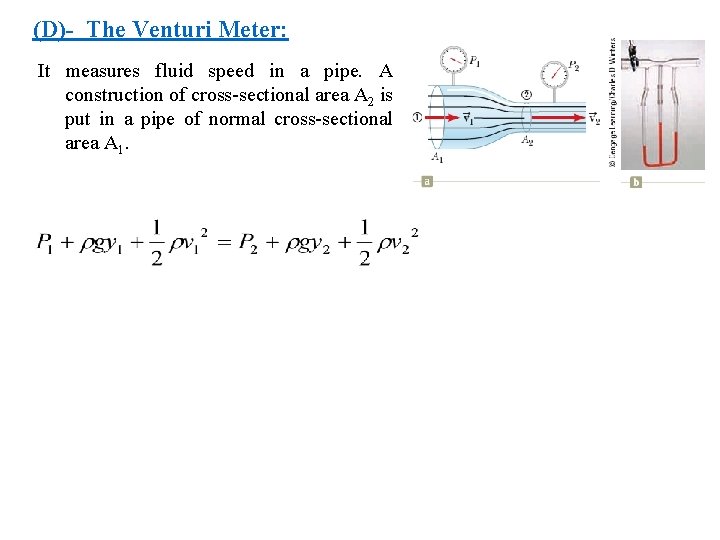
(D)- The Venturi Meter: It measures fluid speed in a pipe. A construction of cross-sectional area A 2 is put in a pipe of normal cross-sectional area A 1.

Chapter 4 Heat

Chapter 5 Thermodynamics

Thank you for your attention!