PERTEMUAN 4 5 dan 6 Matriks Relasi Dan

PERTEMUAN 4, 5 dan 6 Matriks, Relasi Dan Fungsi 1

FUNGSI Misalkan A dan B himpunan. Relasi biner f dari A ke B merupakan suatu fungsi jika setiap di dalam A dihubungkan dengan tepat elemen satu dalam B. Jika f adalah fungsi dari A ke B kita menuliskan f: A B yang artinya f memetakan A ke B. A disebut daerah asal (domain) dari f dan B disebut hasil (codomain) dari f. Nama lain untuk fungsi adalah pemetaan atau transformasi. Kita menuliska f(a) = b jika eleme a 2 di dala n m dihubungkan dengan elemen b din dalam B. A

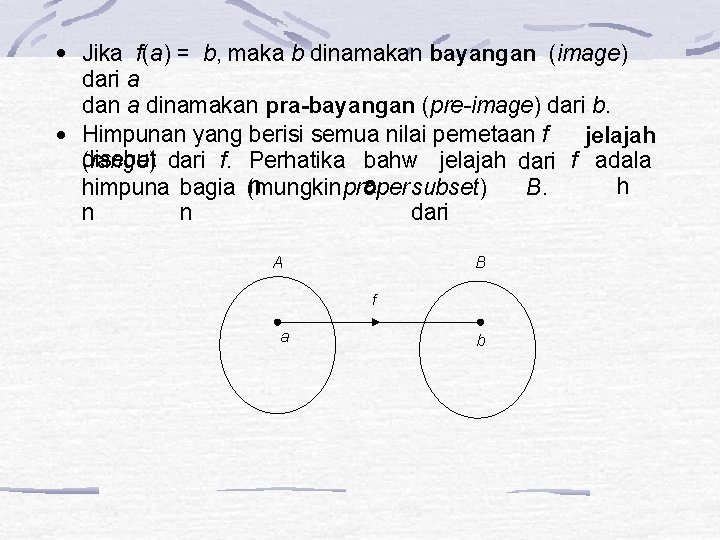
Jika f(a) = b, maka b dinamakan bayangan (image) dari a dan a dinamakan pra-bayangan (pre-image) dari b. Himpunan yang berisi semua nilai pemetaan f jelajah disebut dari f. Perhatika bahw jelajah dari f adala (range) n a h B. himpuna bagia (mungkinpropersubset) n n dari A B f a b 3

Fungsi adalah relasi yang khusus: 1. Tiap elemen di dalam himpunan A harus digunakan oleh prosedur atau kaidah yang mendefinisikan f. 2. Frasa “dihubungkan dengan tepat satu elemen di dalam berartibahw jika (a, b) dan(a, c) f, mak b = c. a a 4

dapa dispesifikasikan t dalam Fungsi diantarany a: 1. Himpunan pasangan terurut. Seperti pada relasi. berbag ai bentuk , 2. Formula pengisian nilai (assignment). Contoh: f(x) = 2 x + 10, f(x) = x 2, dan f(x) = 1/x. 3. Kata-kata jumlah bit 1 Contoh: “f adalah fungsi yang memetakan di dalam suatu string biner”. 4. Kode program (source code) Contoh: Fungsi menghitung function abs(x: integer): integer; |x| begin if x < 0 then abs: =-x else abs: =x; end; 5

Contoh 1. Relasi f = {(1, u), (2, v), (3, w)} dari A = {1, 2, 3} ke B = {u, v, w} adalah fungsi dari A ke B. Di sini f(1) = u, f(2) = v, dan f(3) = w. asal dari f adalah A dan dari f Daerah adala {u, daerah v, w}, yang dalamhal ini sam hasil adalah B. h a Jelajah dengan himpunan B. Contoh 2. Relasi f = {(1, u), (2, u), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w} adalah fungsi dari A ke dari dua elemen Daerah u merupakan bayangan A. asal A, daerah hasilnya adalah B, dan jelajah fungsi 6 adalah {u, B, meskipun fungsi adalah v}.

Contoh 3. Relasi f = {(1, u), (2, v), (3, w)} dari A = {1, 2, 3, 4} ke B = {u, elemen A dipetakan ke B. v, w} buka fungsi, karen tidak semu n a a Contoh 4. Relasi f = {(1, u), (1, v), (2, v), (3, w)} dari A = {1, 2, 3} ke B = {u, v, w} bukan fungsi, karena 1 dipetakan ke dua buah elemen B, yaitu u dan v. Contoh 5. Misalkan f : Z Z didefinisikan oleh f(x) = x 2. Daerah 7 asal dan daerah hasil dari f adalah himpunan bilangan bulat, dan jelajah

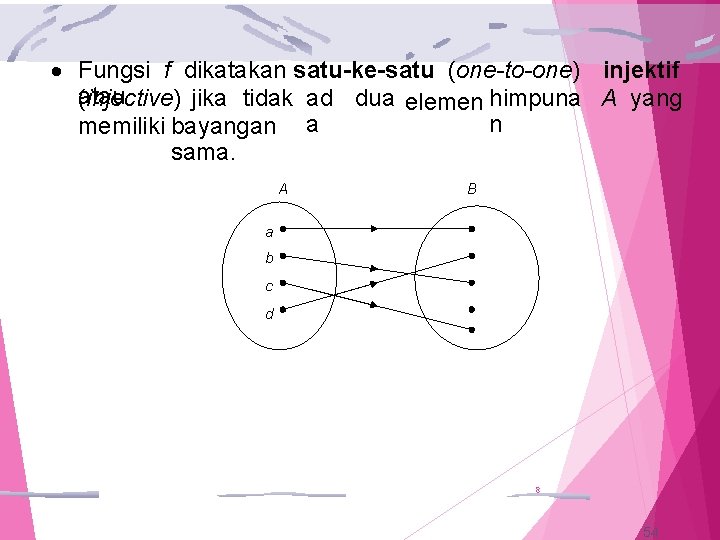
Fungsi f dikatakan satu-ke-satu (one-to-one) injektif atau (injective) jika tidak ad dua elemen himpuna A yang n memiliki bayangan a sama. A B a b c d 8 54

Contoh 6. Relasi f = {(1, w), (2, u), (3, v)} dari A = {1, 2, 3} ke B = {u, w, x} adalah fungsi satu-kev, satu, Tetapi relasi f = {(1, u), (2, u), (3, v)} dari A = {1, 2, 3}ke B ={u, v, w} buka fungsi satu-ken satu, karen f(1) = f(2) = u. a 9 55

x 2 + 1 Contoh 7. Misalkan f : Z Z. Tentukan apakah dan f(x) = x – 1 merupakan fungsi satu-ke-satu? Penyelesaian: (i) f(x) = x 2 + 1 bukan fungsi satu-ke-satu, karena untuk dua xmutlak sama yang bernilai tandanya nilai tetapi berbeda fungsinya sama, misalnya f(2) = f(-2) = 5 padahal – 2 2. (ii) f(x) = x – 1 adalah fungsi satu-ke-satu karena untuk a b, Misalnyauntukx = 2, f(2) = 1 danuntukx = -2, f(-2) = -3. a – 1 b – 1. 10 56

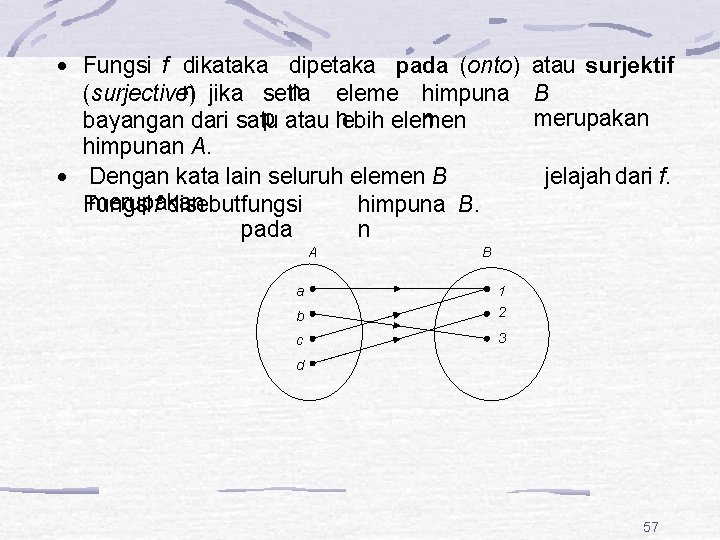
Fungsi f dikataka dipetaka pada (onto) atau surjektif n jika setia n eleme himpuna B (surjective) p atau n n merupakan bayangan dari satu lebih elemen himpunan A. Dengan kata lain seluruh elemen B jelajah dari f. merupakan Fungsif disebutfungsi himpuna B. pada n A B a 1 b 2 c 3 d 11 57

Contoh 8. Relasi f = {(1, u), (2, u), (3, v)} dari A = {1, 2, 3} ke B = v, w} bukan fungsi pad karen w a a {u, tidak termasuk jelajah dari f. Relasi f = {(1, w), (2, u), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w} semu anggot merupakan B merupakan jelajah dari f. a a fungsi pad karen a a 12 58

Contoh 9. Misalkan f : Z Z. Tentukan apakah f(x)x 2=+ 1 dan f(x) = x – 1 merupakan fungsi pada? Penyelesaian: (i) f(x) = x 2 + 1 buka fungsi pada karen tidak semua , a f. nilai bilangan bulat nmerupakan jelajah dari (ii) f(x) = x – 1 adalah fungsi pada karena untuk bilanga bulat yangmemenuh yaitu y = x –n 1 aka setiapy, selalu ada nilai x untukx = y + 1. i, n dipenuh i 13 59

Fungsi f dikatakan satu-keatau berkoresponden dan juga fungsi bijeksi (bijection) jika fungsi satu-ke- satu ia pada. Contoh 10. Relasi f = {(1, u), (2, w), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w} adalah fungsi yang berkoresponden satu-ke- karen f adala fungsi satu-kesatu, fungsi pada. a h satu maupu n 14 60

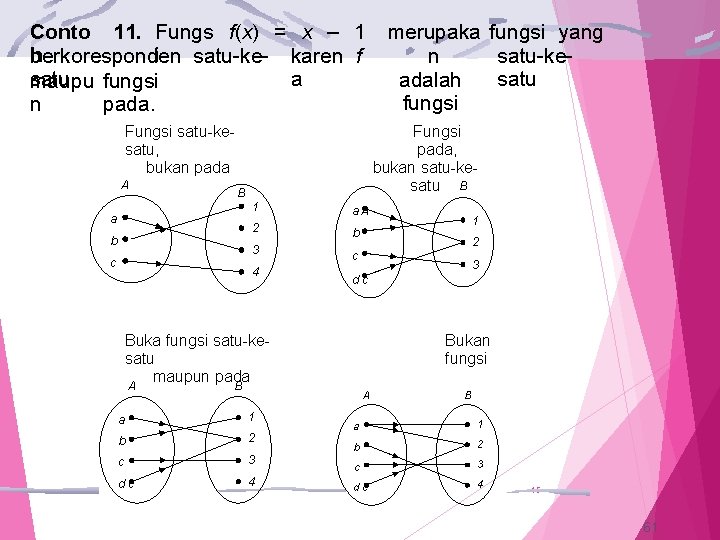
Conto 11. Fungs f(x) = x – 1 h i berkoresponden satu-ke- karen f satu, fungsi a maupu n pada. Fungsi satu-kesatu, bukan pada A Fungsi pada, bukan satu-kesatu B B a b 1 a. A 2 b 3 c 4 c 3 dc Bukan fungsi B A a 1 b 2 c 3 dc 4 1 2 Buka fungsi satu-kesatu maupun pada A merupaka fungsi yang n satu-kesatu adalah fungsi B a 1 b 2 c 3 dc 4 15 61

Jika f adalah fungsi berkoresponden satu-ke-satu dari A ke B, maka kita dapat menemukan balikan (invers) dari f. Balikan fungsi dilambangkan dengan – 1. Misalkan a adalah anggot himpunan A dan b fadala anggot himpuna B, a a n maka f -1(b) = a jika f(a) = h b. Fungsi yang satu-ke-satu sering berkoresponden juga fungsi yang invertible dinamakan (dapat dibalikkan), karena kita dapa mendefinisikan balikannya. Sebua fungsi t fungsi h dikatakan not invertible (tidak dapat dibalikkan) jika ia bukan fungsi yang berkorespond satu-kekaren fungsi en satu, a balikannya tidak ada. 16 62

Contoh 12. Relasi f = {(1, u), (2, w), (3, v)} dari A = {1, 2, 3} ke B = {u, v, w} adala fungsi yang berkoresponden satu-ke-satu. fungsi f h Balikan adala h f -1 = {(u, 1), (w, 2), (v, 3)} Jadi, f adalah fungsi invertible. Contoh 13. Tentukan balikan fungsi f(x) = x– 1. Penyelesaian: Fungsi f(x) = x – 1 adalah fungsi yang berkorespondensatu-ke satu, jadi balikan fungsi tersebut ada. Misalkan f(x) = y, sehingga y = x – 1, maka x = y + 1. Jadi, balikan fungsi balikannya adalah f-1(y) = y +1. 17 63

x 2 = + 1. Contoh 14. Tentukan balikan fungsi f(x) Penyelesaian: Dari Contoh 3. 41 dan 3. 44 kita sudah menyimpulkan bahwa f(x) = xfungsi – 1 bukan fungsi yang berkoresponden tidak ada. Jadi f(x) = x 2 + 1 satu-ke-satu, adala funsgi yang sehingga balikannya , h not invertible. 18 64

Komposisi dari dua buah fungsi. Misalkan g adalah fungsi dari himpunan A ke himpunan B, dan f adalah fungsi dari himpunan B ke himpunan C. A Komposisi f f g, adala dinotasika denga fungsi dari ke C yang dan n g, n h didefinisikan oleh (f g)(a) = f(g(a)) 19 65

Contoh 15. Diberikan fungsi g = {(1, u), (2, u), (3, v)} yang memetakan A = {1, 2, 3} ke B = {u, v, w}, dan fungsi yang memetakan B = {u, v, w} ke C {x, y, z}. Fungsikomposis f = {(u, y), (v, x), (w, i = z)} dari A ke C adalah f g = {(1, y), (2, y), (3, x) } f(x) = x – 1 dan g(x) = x 2 + 1. Contoh Diberikan 16. fungsi Tentukan f g dan g f. Penyelesaian: (i) (f g)(x) = f(g(x)) = f(x 2 + = x 2 + 1 – = x 2. = (x 1– 1)2 + 1 x 2 - 2 x +2. 1) (ii) (g f)(x) = g(f(x)) = g(x – = 20 66

Beberapa Fungsi Khusus 1. Fungsi Floor dan Ceiling Misalkan x adalah bilangan riil, berarti bilangan bulat. x berada di antara dua Fungsi floor dari x: x menyatakan nilai bilangan terbesar yang lebih kecil bulat atau sama dengan x Fungsi ceiling dari x: lebih besar x menyatakan bilangan bulat terkecil atau yang sama dengan x Denga kata lain, fungsi floor membulatka x ke bawah 21 n n , sedangkan fungsi ceiling membulatkan x ke atas. 67

Contoh 17. contohnilai fungsi floor danceiling: Beberapa 3. 5 = 3 3. 5 = 4 0. 5 = 0 0. 5 = 1 4. 8 = 4 4. 8 = 5 – 0. 5 = – 1 – 0. 5 = 0 – 3. 5 = – 4 – 3. 5 = – 3 Contoh 18. Di dalam komputer, data dikodekan dalam untaia n byte, satu byte terdiri atas bit. Jika panjang data 125 bit, 8 maka jumlah untukbahwa merepresentasikan data 125/8 byte = 16 yang byte. Perhatikanlah 16 8 = 128 bit, diperlukan adalah sehingga untuk byte yang terakhir perlu ditambahkan 3 bit ekstra satu agar byte tetap 8 bit (bit ekstra yang ditambahkan untuk menggenapi 8 bit disebut padding bits). 22 68

2. Fungsi modulo Misalkan a adala sembarang h positif. bilangan bulat dan m adala h a mod m memberikan sisa pembagian bilangan bulat bila a dibagi dengan m a mod m = r sedemikian sehingga a = mq denga 0 r < m. + r, n Conto 19. Beberapa contoh fungsi h modulo 25 mod 7 = 4 15 mod 4 = 0 3612 mod 45 = 12 0 mod 5 =75= (sebab – 25 = (– 4) + 3 ) – 25 mod 3 7 23 69

3. Fungsi Faktorial 1 n! 1 2 . (n 1) n 4. Fungsi Eksponensial a a 1 n n Untuk kasus perpangkatan negatif, 1 a n n a 5. Fungsi Logaritmik Fungsi logaritmik berbentuk y a log x x=a , n 0 y 24 70

Fungsi Rekursif Fungsi dikatakan fungsi rekursif jika definisi f fungsinya mengac pada dirinya sendiri. u Contoh n! = 1 2 … (n – 1) n = (n – 1)! n. : 1 , n 0 n! , n n (n 0 1)! Fungsi rekursif disusun dua bagian: oleh (a) Bagian Basis yang berisi nilai awal yang mengacu dirinya tidak pada definisi ini juga menghentika sendiri. sekaligus n Bagian rekursif. (b) Rekurens Bagian ini mendefinisikan argumen fungsi dalam 25 terminologi dirinya sendiri. Setiap kali fungsi mengacu pada dirinya 71

Contoh definisi rekursif dari faktorial: (a) basis: , jika n = n! = 1 0 (b) rekurens: n! = n (n , jika n > 0 1)! 5! dihitung dengan langkah berikut: (1) 5! = 5 (rekurens 4!(2) 4! = 4 3!) 3! = 3 2! (3) 2! = 2 1! (4) 1! = 1 0! (5) 0! = 1 (6) (6’) (5’) (4’) (3’) (2’) (1’) Jadi, 5! = 120. 0! = 1 1! = 1 0! = 1 1 = 1 2! = 2 1 = 2 3! = 3 2 = 6 4! = 4 3! = 4 6 = 24 5! = 5 4! = 5 24 = 120 26 72

Contoh 20. Di bawah ini adalah contoh-contoh fungsi rekursif lainnya: , x 0 0 1. F(x) 2 F(x 1) x , x 0 2 2. Fungsi Chebysev 1 x T (n, x) 2 x. T (n 1, x) T (n 2, x) 3. Fungsi fibonacci: , n 0 0 1 f (n) , n f (n 1) 1 f (n 2) , n 1 , n 0 , n 1 27 73

Relasi Kesetaraan DEFINISI. Relasi R pada A disebut relasihimpunan kesetaraan (equivalence relation) jika refleksif, ia setangkup dan menghantar. 28 74

Secara intuitif, di dalam relasi kesetaraan, dua benda berhubungan jika keduanya memiliki beberapa sifat yang sama atau memenuhi beberapa persyaratan yang sama. Dua elemen yang dihubungkan dengankesetaraan relasi dinamakan (equivalent). setara 29 75

Contoh: A = himpunan mahasiswa, R relasi pada A: (a, b) R jika a satu angkatan dengan b. seangkatan R refleksif: setiap mahasiswa dengan dirinya sendiri R setangkup: jika a seangkatan dengan b, maka b pasti seangkatan dengan. jika a seangkatan dengan b dan R amenghantar: b seangkatan dengan c, maka pastilah a seangkatan dengan c. Dengan demikian, R adalah relasi kesetaraan. 30 76

Relasi Pengurutan Parsial DEFINISI. Relasi R pada himpunan S dikatakan relasi pengurutan parsial (partial ordering relation) jika ia refleksif, tolaksetangkup, dan menghantar. bersama-sama dengan relasi Himpunan S R disebut himpunan terurut secara parsial (partially ordered set, atau poset), dan dilambangkan dengan (S, R). 31 77

Contoh: Relasi pada himpunan bilangan bulat adalah relasi parsial. pengurutan Alasan: Relasi refleksif, karena a untuk setiap a bilangan bulat a; a b dan Relasi tolak-setangkup, karena jika b a, maka a = b; Relasi menghantar, karena jika a dan b c maka a b c. 32 78

Contoh: Relasi “habis membagi” pada himpunan bilangan bulat adalah relasi pengurutan parsial. Alasan: relasi “habis bersifat membagi” refleksif, tolak-setangkup, dan menghantar. 33 79

Secara intuitif, di relasi dalam buah benda pengurutan parsial, salah -dua lebih kecil (lebih besar) satunya daripada, berhubungan -saling atau lebih rendah (lebih tinggi) jika daripada menurut sifat atau lainnyatertentu. kriteria 34 80

Istilah pengurutan menyatakan bahwa benda-benda di dalam himpunan tersebut dirutkan berdasarkan sifat atau kriteria tersebut. Ada juga kemungkinan dua buah benda di dalam himpunan tidak berhubungan dalam suatu relasi pengurutan parsial. Dalam hal demikian, kita tidak dapat membandingkan keduanya sehingga tidak dapat diidentifikasi Itulah alasanlebih digunakan istilah mana yang besar atau lebih kecil. pengurutan parsial atau pengurutan tak-lengkap 81 35

Klosur Relasi (closure of relation) Contoh 1: Relasi R = {(1, 1), (1, 3), (2, 3), (3, 2)} pada himpunan A = {1, 3} 2, tidak refleksif. Bagaimana membuat relasi refleksif yang sesedikit mungkin dan mengandung R? 36 82

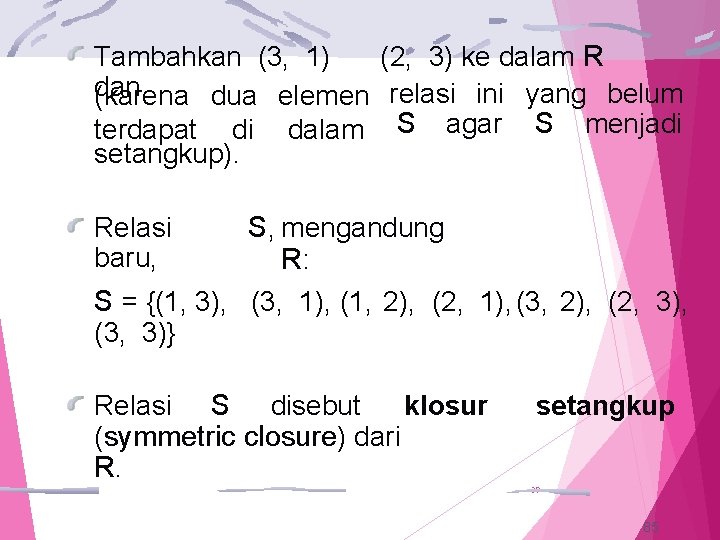
Tambahkan (2, 2) dan (3, 3) ke dalam R belum (karena dua elemen relasi ini yang terdapat di dalam R) Relasi baru, S, mengandung R, yaitu S = {(1, 1), (1, 3), (2, 2), (2, 3), (3, 2), (3, 3) } Relasi disebut klosur refleksif (reflexive dari R. S closure) 37 83

Contoh 2: Relasi R = {(1, 3), (1, 2), (2, 1), (3, 2), (3, 3)} pada himpunan A = {1, 2, 3} tidak setangkup. Bagaimana membuat relasi setangkup dan yang sesedikit mungkin mengandung R? 38 84

Tambahkan (3, 1) (2, 3) ke dalam R dan (karena dua elemen relasi ini yang belum terdapat di dalam S agar S menjadi setangkup). S, mengandung R: S = {(1, 3), (3, 1), (1, 2), (2, 1), (3, 2), (2, 3), (3, 3)} Relasi baru, Relasi S disebut klosur (symmetric closure) dari R. setangkup 39 85

Misalkan R adalah relasi pada himpunan A. R dapat memiliki atau tidak memiliki sifat P, seperti refleksif, setangkup, atau menghantar. Jika terdapat relasi S dengan sifat P yang mengandung sehingga. R S sedemikian adalah himpunan bagian dari setiap relasi dengan sifat P yang mengandung disebut klosur. R, (closure) atau maka dari R [ROS 03]. S tutupan 40 86

Klosur Refleksif Misalkan R adalah sebuah himpunan A. relasi pada Klosur refleksif dari R adalah R , yang dalam hal ini = {(a, a) | a A}. 41 87

Contoh: R = {(1, 1), (1, 3), (2, 3), (3, 2)} adalah relasi pada A = {1, 2, 3} maka = {(1, 1), (2, 2), (3, 3)}, sehingga klosur refleksif dari R adalah R = {(1, 1), (1, 3), (2, 3), (3, 2)} {(1, 1), (2, 2), (3, 3)} = {(1, 1), (1, 3), (2, 2), (2, 3), (3, 3)} 2), 42 88

Contoh: Misalkan R adalah relasi {(a, b) | a b} pada himpunan bilangan bulat. Klosur refleksif dari R adalah R = {(a, b) | a b} {(a, a) | a Z} = {(a, b) | a, b Z} 43 89

Klosur setangkup Misalkan R adalah sebuah himpunan A. relasi pada Klosur setangkup dari R adalah R R-1, dengan R-1 = {(b, a) | (a, b) a R}. 44 90

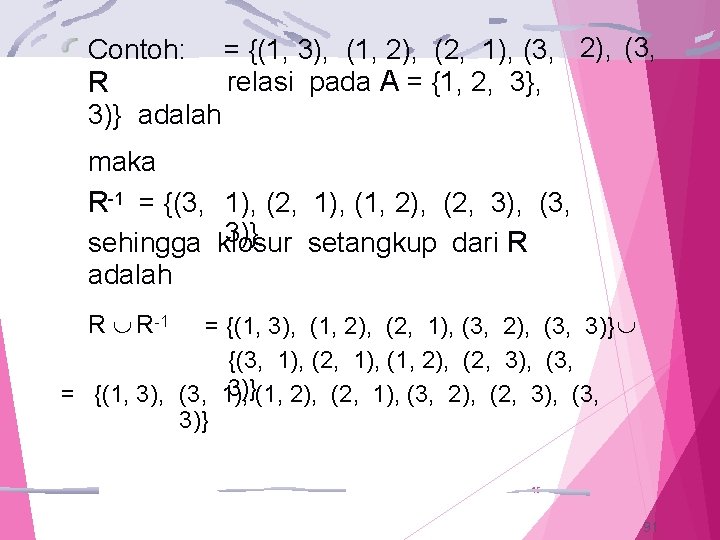
Contoh: = {(1, 3), (1, 2), (2, 1), (3, 2), (3, relasi pada A = {1, 2, 3}, R 3)} adalah maka R-1 = {(3, 1), (2, 1), (1, 2), (2, 3), (3, 3)} sehingga klosur setangkup dari R adalah R R-1 = {(1, 3), (1, 2), (2, 1), (3, 2), (3, 3)} {(3, 1), (2, 1), (1, 2), (2, 3), (3, 3)}(1, 2), (2, 1), (3, 2), (2, 3), (3, = {(1, 3), (3, 1), 3)} 45 91

Contoh: Misalkan R adalah relasi {(a, b) | a habis membagi b} pada himpunan bilangan bulat. Klosur setangkup dari R adalah R R-1 = {(a, b) | a habis b} {(b, a) | b habis membagi a} = {(a, b) | a habis membagi b atau b habis membagi a} 46 92

Klosur menghantar Pembentukan klosur menghantar lebih sulit daripada dua buah klosur sebelumnya. Contoh: R = {(1, 2), (1, 4), (2, 1), (3, 2)} adalah relasi A {1, 2, 3, 4}. = R tidak transitif karena tidak mengandung semua pasangan (a, c) sedemikian (a, b) dan (b, c) di dalamsehingga R. Pasangan (a, yang tidak terdapat di c. R ) adalah (1, 1), dalam (2, 2), (2, 4), dan (3, 1). 47 93

ini ke dalam Penambahan semua R pasangan sehingga menjadi S = {(1, 2), (1, 4), (2, 1), (3, 2), (1, 1), (2, 2), (2, 4), (3, 1)} tidak menghasilkan relasi yang bersifat menghantar karena, terdapat (3, 1) misalnya S dan (1, 4) S, tetapi (3, 4) S. 48 94

Kosur menghantar dari R adalah R* = R 2 R 3 … Rn Jika adalah matriks yang MR merepresentasikan R pada sebuah dengan himpunann elemen, maka matriks klosur menghantar R* adalah M R* MR[2] MR[3] … MR[n] 49 95

Misalkan R = {(1, 1), (1, 3), (2, 2), (3, 1), (3, klosur menghantar dari R. Penyelesaian: Matriks yang merepresentasikan relasi R adalah 1 0 1 MR = 0 1 0 2)} adala relasi pad himpuna A = {1, 2, 3}. Tentuka h a n n 1 0 1 Maka, matriks klosur menghantar dari R adalah M [2] M [3] M R* R R MR Karen a M R[2] MR 1 1 1 M R 0 0 1 1 1 1 dan M R[3] 1 1 1 M R[2] M R 0 1 1 1 maka 1 0 1 1 1 1 0 1 0 = 0 1 0 1 1 1 1 * Dengan demikian, R = {(1, 1), (1, 2), (1, 3), (2, 2), (3, 1), (3, 2), (3, 3) } M R* 50 96

Aplikasi klosur menghantar Klosur menghantar menggambarkan bagaimana pesan dapat dikirim dari satu kota ke kota lain baik melalui antara sebanyak mungkin melalui hubungan komunikasi langsung kota atau [LIU 85]. 51 97

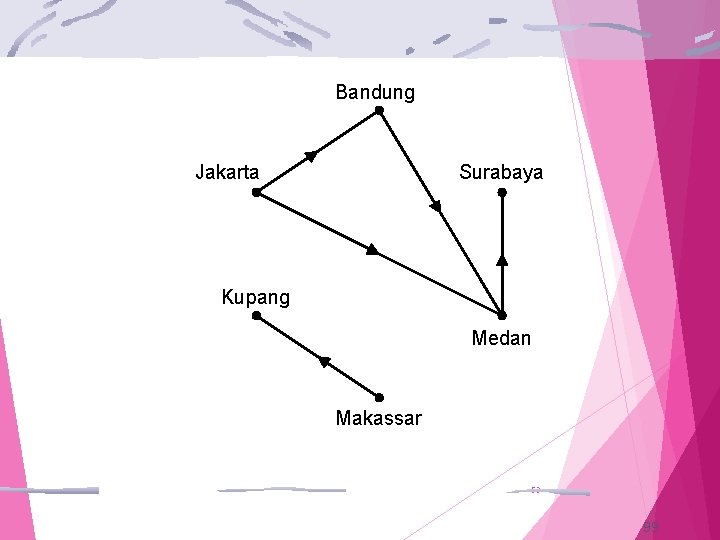
Misalkan jaringan komputer mempunyai pusat data di Jakarta, Bandung, Surabaya, Medan, Makassar, dan Kupang. Misalkan R adalah relasi yang mengandung (a, b) jika saluran terdapat telepon dari kota ke kota b. a 52 98

Bandung Jakarta Surabaya Kupang Medan Makassar 53 99

Karena tidak semua link langsung dari satu kota ke kota lain, maka pengiriman data dari Jakarta ke Surabaya tidak dapat dilakukan secara langsung. Relasi R tidak menghantar karena ia tidak mengandung semua pasangan pusat data dapat yang (baik link langsung atau tidak dihubungkan langsung). Klosur menghantar adalah yang paling relasi yang berisi pasangan minimal pusat data yang semualink mempunyai atau tidak langsung dan mengandunglangsung R. 54 100

Tugas 1 2 3 4 5 55