Urutan Parsial Partial Orders Relasi R pada himpunan

Urutan Parsial (Partial Orders) • Relasi R pada himpunan X disebut urutan parsial jika R Frefleksif, Fantisimetris dan Ftransitif • Ketiga persyaratan tersebut harus dipenuhi • Contoh: 0

• Relasi >= pada himpunan bilangan bulat adalah relasi pengurutan parsial karena: – refleksif karena a>=a untuk setiap bilangan bulat a – anti simetris karena jika a>=b dan b>= a maka a=b – transitif karena jika a>=b dan b >=c maka a>=c • Relasi habis membagi adalah relasi pengurutan parsial karena: – Refeksif karena setiap bilangan bulat habis membagi dirinya sendiri – Anti simetris karena a habis membagi b, berarti b tidak habis membagi a kecuali jika a=b – Transitif karena jika a habis membagi b dan b habis membagi c maka a habis membagi c

Invers • Misalkan R adalah relasi dari X ke Y maka invers dari R adalah relasi dari Y ke X • Notasi : R-1 • Invers didefinisikan : R-1 = {(y, x) | (x, y) R} Contoh: R = {(2, 4), (2, 6), (3, 3), (3, 6), (4, 4)} R-1 = {(4, 2), (6, 2), (3, 3), (6, 3), (4, 4)} 2

• Matriks yang merepresentasikan relasi R-1, misalkan N, diperoleh dengan melakukan transpose terhadap matriks M M= 3 2 0 3 1 4 0 4 1 0 1 6 1 1 0 N = M-1 = 2 3 0 4 1 6 1 3 1 0 1 4 0 1 0

• Misalkan P = {2, 3, 4} dan Q = {2, 4, 8, 9, 15} jika didefinisikan relasi R dari P ke Q dengan: (p, q) R jika p habis membagi q • Inversinya?

Relasi Keekuivalenan • Teorema 1 : Misalkan S adalah partisi dari himpunan X. Definisikan x. Ry untuk mengartikan bahwa untuk beberapa himpunan S di S, baik x maupun y berada di S, maka R refleksif, simetris, dan transitif • Sebuah relasi yang refleksif, simetris dan transitif pada himpunan X disebut relasi keekuivalenan pada X (equivalence relation on X)

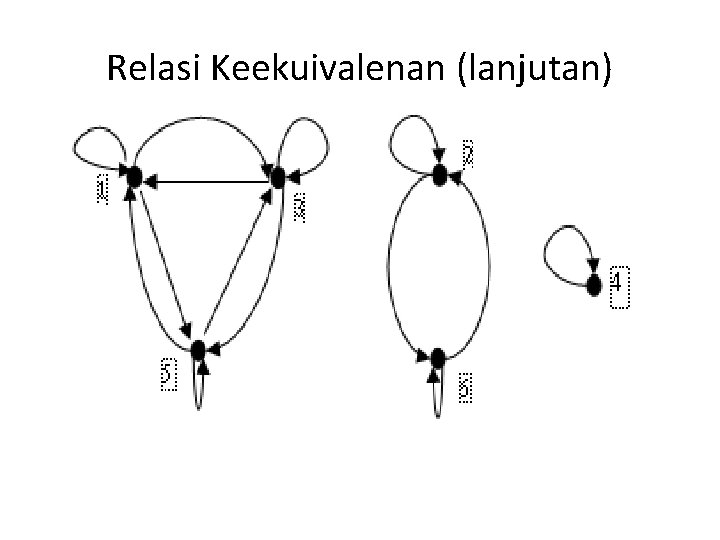
Relasi Keekuivalenan (lanjutan) • Contoh : S = {{1, 3, 5}, {2, 6}, {4}} X = {1, 2, 3, 4, 5, 6} R = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5), (2, 2), (2, 6), (6, 2), (6, 6), (4, 4)} • Digraf relasi dari R harus : F Refleksif : terdapat sebuah loop pada setiap ujungnya F Simetris : untuk setiap rusuk berarah dari v ke w juga terdapat rusuk berarah dari w ke v F Transitif : jika terdapat sebuah rusuk berarah dari x ke y dan rusuk berarah dari y ke z maka terdapat rusuk berarah dari x ke z

Relasi Keekuivalenan (lanjutan)

Teorema 2 • Misalkan R sebuah relasi keekuivalenan pada himpunan X. Untuk setiap a X, misalkan : {a} = {x X | x. Ra} Sehingga : S = {[a] | a X} adalah partisi dari X • Misalkan R adalah relasi keekuivalenan pada himpunan X. Himpunan-himpunan [a] yang didefinisikan pada Teorema 2 disebut kelas keekuivalenan dari X yang diberikan oleh relasi R

Contoh • S = {{1, 3, 5}, {2, 6}, {4}} X = {1, 2, 3, 4, 5, 6} R = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5), (2, 2), (2, 6), (6, 2), (6, 6), (4, 4)} Kelas keekuivalenan [1] yang mengandung 1 terdiri dari semua y sehingga (1, y) R. Oleh karena itu : [1] = {1, 3, 5} Kelas ekuivalenan yang tersisa didapatkan dengan cara yang sama : [3] = [5] = {1, 3, 5} [2] = [6] = {2, 6} [4] = {4}

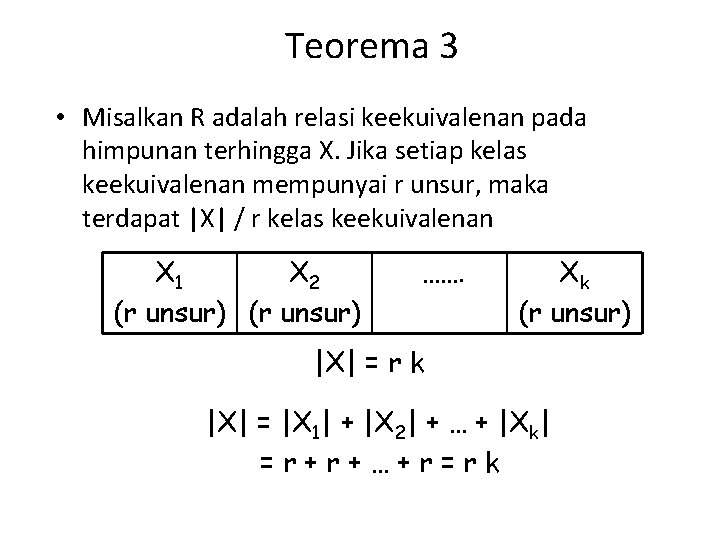
Teorema 3 • Misalkan R adalah relasi keekuivalenan pada himpunan terhingga X. Jika setiap kelas keekuivalenan mempunyai r unsur, maka terdapat |X| / r kelas keekuivalenan X 1 X 2 (r unsur) ……. Xk (r unsur) |X| = r k |X| = |X 1| + |X 2| + … + |Xk| =r+r+…+r=rk

Klosur Relasi • Klosur relasi terjadi jika : FRelasi tidak refleksif menjadi refleksif Klosur refleksif (Reflexive Closure) FRelasi tidak simetris menjadi simetris Klosur simetris (Symmetric Closure) FRelasi tidak transitif menjadi transitif Klosur transitif (Transitive Closure)

Klosur refleksif (Reflexive Closure) • Klosur refleksif dari R adalah : R , dimana = {(a, a)|a A} • Contoh : 1. A = {1, 2, 3} R = {(1, 1), (1, 3), (2, 3), (3, 2)} tidak refleksif Supaya bersifat refleksif maka = {(1, 1), (2, 2), (3, 3)} Sehingga klosur refleksif dari R adalah : R = {(1, 1), (1, 3), (2, 3), (3, 2)} (1, 1), (2, 2), (3, 3)} = {(1, 1), (1, 3), (2, 2), (2, 3), (3, 2), (3, 3)} 2. R = {(a, b)|a b} pada himpunan bilangan bulat Maka klosur refleksif dari R adalah : R = {(a, b)|a b} {(a, a)|a Z} = {(a, b)|a Z}

Klosur Simetris (Symmetric Closure) • Klosur simetris dari R adalah : R R-1 , dimana R-1 = {(a, b)| (b, a) a R} • Contoh : 1. A = {1, 2, 3} R = {(1, 3), (1, 2), (2, 1), (3, 2), (3, 3)} Supaya bersifat simetris maka R-1 = {(3, 1), (2, 1), (1, 2), (2, 3), (3, 3)} Sehingga klosur simetris adalah : R R-1 = {(1, 3), (1, 2), (2, 1), (3, 2), (3, 3)} {(3, 1), (2, 1), (1, 2), (2, 3), (3, 3)} = {(1, 3), (3, 1), (1, 2), (2, 1), (3, 2), (2, 3), (3, 3)} 2. R = {(a, b)|a habis membagi b} pada himpunan bilangan bulat Maka klosur simteris dari R adalah : R R-1 = {(a, b)|a habis membagi b} {(b, a)|b habis membagi a} = {(a, b)|a habis membagi b atau b habis membagi a}

Klosur Transitif (Transitive Closure) • Klosur transitif dari R adalah :

Contoh A = {1, 2, 3} R = {(1, 1), (1, 3), (2, 2), (3, 1), (3, 2)} Matriks yang merepresentasikan relasi R adalah : Klosur transitif dari R adalah : Karena Maka Sehingga klosur transitif R* : {(1, 1), (1, 2), (1, 3), (2, 2), (3, 1), (3, 2), (3, 3)}

Latihan 1. Jika A = {0, 1, 2, 3} R = {(0, 1), (1, 2), (2, 0), (2, 2)} Tentukan : a. Klosur transitif b. Klosur simetris 2. Jika A = {1, 2, 3, 4} R = {(2, 1), (2, 3), (3, 1), (3, 4), (4, 1), (4, 3)} Tentukan : a. Klosur refleksif b. Klosur simetris c. Klosur transitif