MATRIKS INVERS PENGERTIAN MATRIKS INVERS MENGHITUNG SIFAT MATRIKS

MATRIKS INVERS Ø PENGERTIAN MATRIKS INVERS Ø MENGHITUNG Ø SIFAT- MATRIKS INVERS SIFAT MATRIKS INVERS 1

PENGERTIAN MATRIKS INVERS Invers matriks adalah lawan atau kebalikan suatu matriks dalam perkalian Dilambangkan dengan A-1 Definisi: Jika matriks A dan B sedemikian sehingga A x B = B x A = I , dimana I matriks identitas maka B disebut invers dari A dan A invers dari B. Karena invers matriks A dilambangkan dengan A-1 maka berlaku: A x A-1 = A-1 x A= I Matriks yang mempunyai invers disebut invertible atau non singular ( ) 2

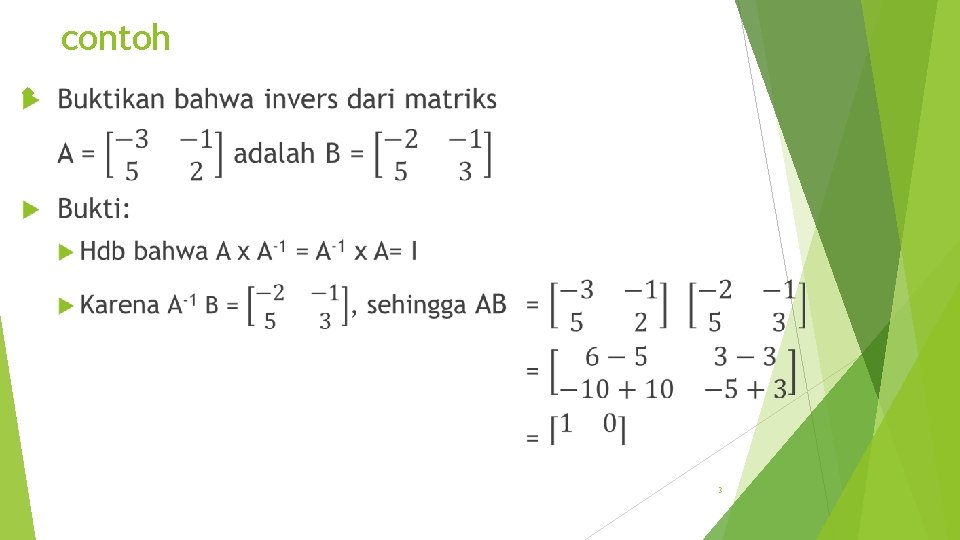
contoh 3

MENGHITUNG MATRIKS INVERS Untuk mendapatkan A-1, dengan cara : 1. Cara Perkalian Matriks 2. Metode Matriks Adjoint / Determinan 3. Metode Operasi Baris Elementer (OBE) atau Transformasi Elementer Baris (TEB) 4

1. Cara perkalian matriks destyrakhmawati@yahoo. com 2/23/2021 5

destyrakhmawati@yahoo. com 2/23/2021 6

2. Metode Matriks Adjoint / Determinan destyrakhmawati@yahoo. com 2/23/2021 7

destyrakhmawati@yahoo. com 2/23/2021 8

v Contoh : Carilah invers dari A = v Solusi : C = M = d 11 11 C 21 = - M 21 = - b C 12 = - M 12 = - c adj(A) = C 22 = M 22 = a = | A | = ad – bc A-1 = destyrakhmawati@yahoo. com = 2/23/2021 9

v Carilah invers dari A = v Solusi : C 11 = M 11 = - 5 C 21 = - M 21 = 4 C 31 = M 31 = - 4 C 12 = - M 12 = 1 C 22 = M 22 = - 2 C 32 = - M 32 = 0 C 13 = M 13 = 1 C 23 = - M 23 = 0 C 33 = M 33 = 2 = adj(A) = |A| = a 11 C 11 + a 12 C 12 + a 13 C 13 = (2)(-5) + (4)(1) = - 2 A-1 = destyrakhmawati@yahoo. com = = 2/23/2021 10

3. Metode Operasi Baris Elementer (OBE) atau Transformasi Elementer Baris (TEB) destyrakhmawati@yahoo. com 2/23/2021 11

v A matriks persegi non singular, dengan OBE terhadap A dapat direduksi menjadi bentuk normal I sedemikian hingga : P A = I v P hasil penggandaan matriks elementer (baris). v Selanjutnya, PA =I P-1 P A = P-1 I IA = P-1 v Jadi hasil penggandaan matriks elementer (baris) ini adalah invers dari matriks A. v Teknis pencarian invers dengan OBE : (A | I) ~ (I | A-1) destyrakhmawati@yahoo. com 2/23/2021 12

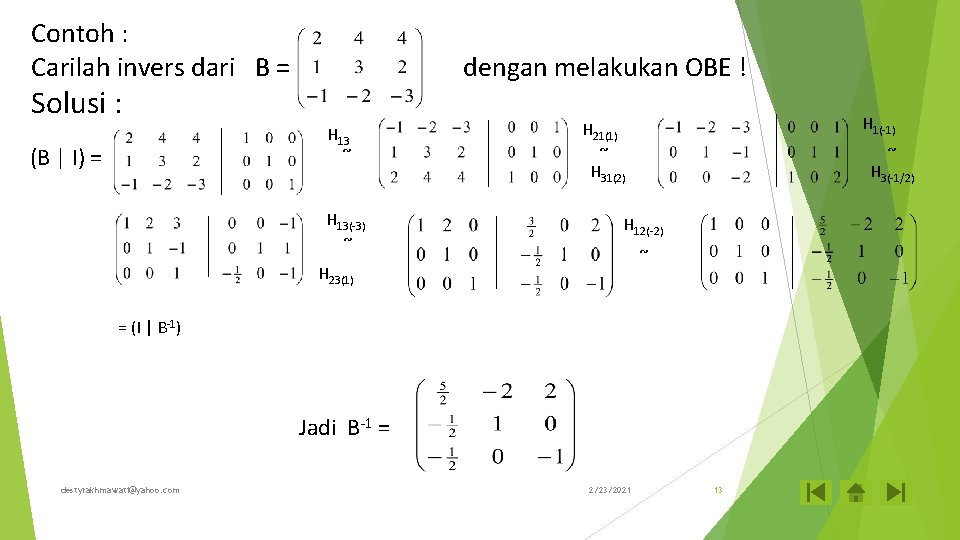
Contoh : Carilah invers dari B = dengan melakukan OBE ! Solusi : H 13 ~ (B | I) = H 13(-3) ~ H 1(-1) H 21(1) ~ H 31(2) ~ H 3(-1/2) H 12(-2) ~ H 23(1) = (I | B-1) Jadi B-1 = destyrakhmawati@yahoo. com 2/23/2021 13

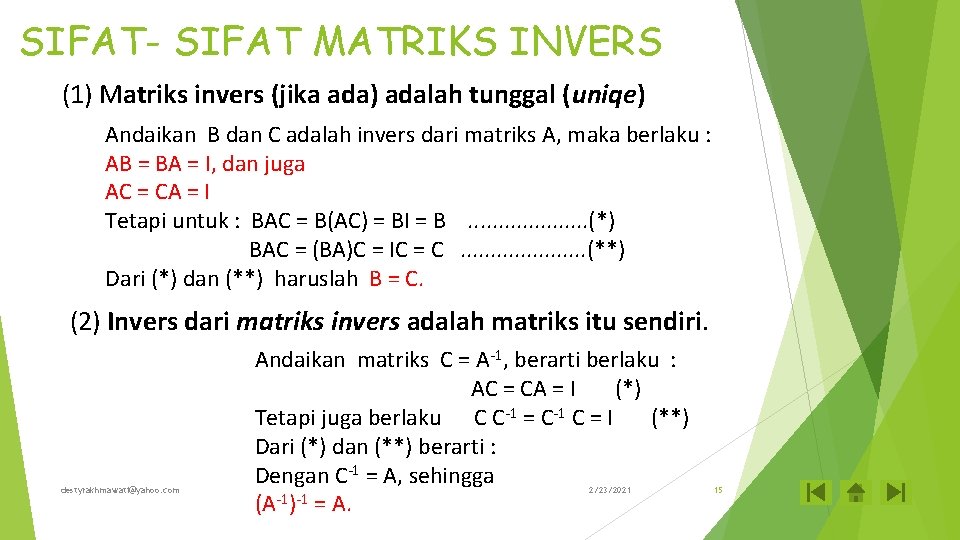
SIFAT- SIFAT MATRIKS INVERS (1) Matriks invers (jika ada) adalah tunggal (uniqe) Andaikan B dan C adalah invers dari matriks A, jika AB = BA = I, dan AC = CA = I, maka B = C. (2) Invers dari matriks invers adalah matriks itu sendiri (A-1)-1 = A. (3) Matriks invers bersifat nonsingular (determinannya tidak nol ) det (A-1) = (4) Jika A dan B masing-masing adalah matriks persegi berdimensi n, dan berturut-turut A-1 dan B-1 adalah invers dari A dan B, maka berlaku hubungan : (AB)-1 = B-1 A-1 (5) Jika matriks persegi A berdimensi n adalah non singular, maka berlaku (AT)-1 = (A-1)T. destyrakhmawati@yahoo. com 2/23/2021 14

SIFAT- SIFAT MATRIKS INVERS (1) Matriks invers (jika ada) adalah tunggal (uniqe) Andaikan B dan C adalah invers dari matriks A, maka berlaku : AB = BA = I, dan juga AC = CA = I Tetapi untuk : BAC = B(AC) = BI = B. . . . . (*) BAC = (BA)C = IC = C. . . . . (**) Dari (*) dan (**) haruslah B = C. (2) Invers dari matriks invers adalah matriks itu sendiri. destyrakhmawati@yahoo. com Andaikan matriks C = A-1, berarti berlaku : AC = CA = I (*) Tetapi juga berlaku C C-1 = C-1 C = I (**) Dari (*) dan (**) berarti : Dengan C-1 = A, sehingga (A-1)-1 = A. 2/23/2021 15

(3) Matriks invers bersifat nonsingular (determinannya tidak nol ) det (A A-1) = det (A) det (A-1) det (I) = det (A) det (A-1) 1 = det (A) det (A-1) ; karena det (A) 0 , maka : det (A-1) = (4) Jika A dan B masing-masing adalah matriks persegi berdimensi n, dan berturut-turut A-1 dan B-1 adalah invers dari A dan B, maka berlaku hubungan : (AB)-1 = B-1 A-1 di sisi lain : (AB)-1 (AB) (B-1 A-1) (AB) = (AB)-1 (AB) = A(BB-1) A-1 = B-1(A-1 A) B =I = A I A-1 = B-1 I B = A A-1 = I = B-1 B = I Menurut sifat (1) di atas matriks invers bersifat uniqe (tunggal), karena itu dari (*) dan (**) dapatlah disimpulkan bahwa (AB)-1 = B-1 A-1. destyrakhmawati@yahoo. com 2/23/2021 16 (*) (**)

(5) Jika matriks persegi A berdimensi n adalah non singular, maka berlaku (AT)-1 = (A-1)T. Menurut sifat determinan : AT = A 0, oleh sebab itu (AT)-1 ada, dan haruslah : (AT)-1 AT = AT (AT)-1 = I (*) Di sisi lain menurut sifat transpose matriks : (A A-1)T= (A-1)T AT IT= (A-1)T AT = I, hubungan ini berarti bahwa (A-1)T adalah juga invers dari AT. Padahal invers matriks bersifat tunggal, oleh karena itu memperhatikan (*), haruslah : (A-1)T = (AT)-1. destyrakhmawati@yahoo. com 2/23/2021 17