ONDE GRAVITAZIONALI Notazioni Segnatura h Equazioni di Einstein


























- Slides: 26

ONDE GRAVITAZIONALI

Notazioni Segnatura h

Equazioni di Einstein

Approssimazione campo debole ≤ |hmn| Trasformazione della metrica Nel caso di campo debole

Approssimazione per tensore di Riemann

Definition

Gauge armonica (o di Lorenz) Utilizziamo la libertà di scelta di coordinate Che porta h in h’ secondo per cercare un sistema di coordinate tale che:

Invertendo Se quindi Occorre trovare una funzione Tale che

La soluzione esiste sempre perché l’operatore di D’Alambert è invertibile Detta G la funzione di Green La soluzione è 6 componenti indipendenti

Gauge TT Fuori dalla sorgente Altra trasformazione Con In questo modo si preserva Definiamo Perché le derivate commutano

Sottrazione Poiché per queste trasformazioni vale sempre che Allora significa che dal tensore Possiamo sottrarre le funzioni per le quali vale che soddisfa Che dipendono dalle quattro funzioni arbitrarie Per cui la relazione rimane soddisfatta

Scelta 1) Scegliamo tale che la traccia (Questo ovviamente si può sempre fare) 2) Le altre tali che poiché diventa la condizione con ma poiché abbiamo messo

Conclusione TT Sopravvivono solo le componenti spaziali con in più la condizione di traccia nulla Quindi dai 10 gradi di libertà che aveva la matrice hmn simmetrica, con le prime quattro condizioni di trasversalità sono rimasti 6 parametri liberi e con le quattro della Gauge TT sono rimasti solo due parametri liberi

Forma generale per un onda che si propaga lungo l’asse z

Effetto sulle masse. Equazione della deviazione geodetica Equazione delle geodetica Consideriamo una seconda masse di coordinate Al primo ordine otteniamo

Riscritta in modo elegante Dove la derivata covariante di un vettore Vm(x) lungo la curva x(t) è definita come

Sistema TT Supponiamo che una massa sia a riposo nel nostro sistema TT per Questo perché inizialmente velocità è zero Questo per la nostra cara vecchia approssimazione Nella TT questo è zero….

In TT a particle at rest remain at rest Quindi nel sistema TT anche con il passaggio dell’onda le coordinate rimangono costanti. E’ utilissimo verificarlo con l’equazione della deviazione geodetica. Ci aspettiamo che la differenza tra le coordinate z non vari pur in presenza dell’onda! L’equazione della deviazione geodetica stabilisce:

Deviazione geodetica in TT recall per ipotesi

La differenza di coordinate rimane costante recall =0 perché o è zero il termine oppure è zero la derivata rispetto al tempo Se inizialmente le masse sono ferme una rispetto all’altra allora Rimangono «ferme» anche quando passa l’onda gravitazionale, ovvero la differenza tra le loro coordinate rimane costante

Proper distance Photons =0 =L ct = (1 + ½h) L Attenzione alla polarizzazione

Sistema di riferimento del laboratorio in caduta libera Consideriamo un sistema di riferimento in caduta libera con coordinate fissate da un regolo rigido (per esempio un drag-free satellite) Nell’intorno del punto P origine del nostro sistema di coordinate la metrica è non dipendente linearmente dalle coordinate ma dipende dalle derivate seconde Dove R è valutato in P

Sistema di riferimento sulla terra Sulla terra vi è l’accelerazione –a e la rotazione w Scrivendo l’equazione della geodetica e trascurando i termini al secondo ordine In x con questa metrica otteniamo Ovvero recuperimao accelerazione di gravità e forza di Coriolis e fi forza esterna

Effetto delle onde gravitazionali Ripartiamo dalla deviazione geodetica 1) La connessione affine è zero in P 2) dx/dt è trascurabile rispetto a dx 0/dt e La derivata della connessione affine calcolata in P è diversa da zero solo se coinvolge le derivate seconde delle coordinate spaziali. Quindi la parte temporale della derivata della equazione precedente è zero e si ha

Dunque in P il tensore di Riemann vale E l’equazione della deviazione geodetica può essere scritta La parte temporale rimane al secondo ordine

Equazione finale Nella teoria linearizzata il tensore di Riemann è invariante! Quindi lo calcoliamo In TT che è la gauge che più ci è facile
 Indicatori di posizione gravitazionali
Indicatori di posizione gravitazionali Rapporto tra due aree con notazione scientifica
Rapporto tra due aree con notazione scientifica Atividade 6 ano projeto de vida
Atividade 6 ano projeto de vida Scomposizione denominatore equazioni fratte
Scomposizione denominatore equazioni fratte 4 equazioni di maxwell
4 equazioni di maxwell Equazioni di navier stokes
Equazioni di navier stokes Quando un'equazione è impossibile
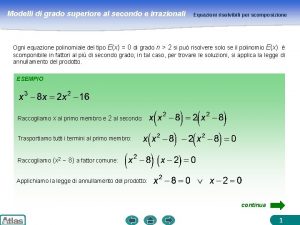
Quando un'equazione è impossibile Equazioni irrazionali
Equazioni irrazionali Oscillatore armonico
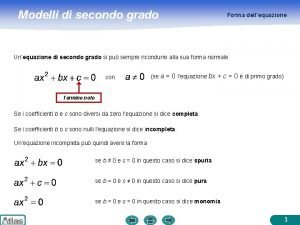
Oscillatore armonico Equazione di secondo grado
Equazione di secondo grado Regole equazioni di secondo grado
Regole equazioni di secondo grado Disequazioni
Disequazioni Disequazioni con più valori assoluti
Disequazioni con più valori assoluti Relazione di mayer
Relazione di mayer Equazione indeterminata
Equazione indeterminata Disequazioni di secondo grado ppt zanichelli
Disequazioni di secondo grado ppt zanichelli Equazioni
Equazioni Equazioni esponenziali
Equazioni esponenziali Vincolo carrello nella realtà
Vincolo carrello nella realtà Bilanciamento
Bilanciamento Equazioni lineari definizione
Equazioni lineari definizione Rdf raddrizzamento download
Rdf raddrizzamento download Equazioni storia
Equazioni storia Equazione di continuità
Equazione di continuità Disequazioni di grado superiore al secondo spiegazione
Disequazioni di grado superiore al secondo spiegazione Ihcca
Ihcca Trasformazione di lorentz
Trasformazione di lorentz