Come le frazioni e le proporzioni le equazioni

























- Slides: 35


Come le frazioni e le proporzioni, le equazioni costituiscono validi strumenti per risolvere problemi, che vengono chiamati di 1°, 2°…a seconda del grado dell’equazione risolvente. Per fissare le idee, analizziamo qualche situazione problematica ricavata da contesti diversi e proviamo a risolverla…

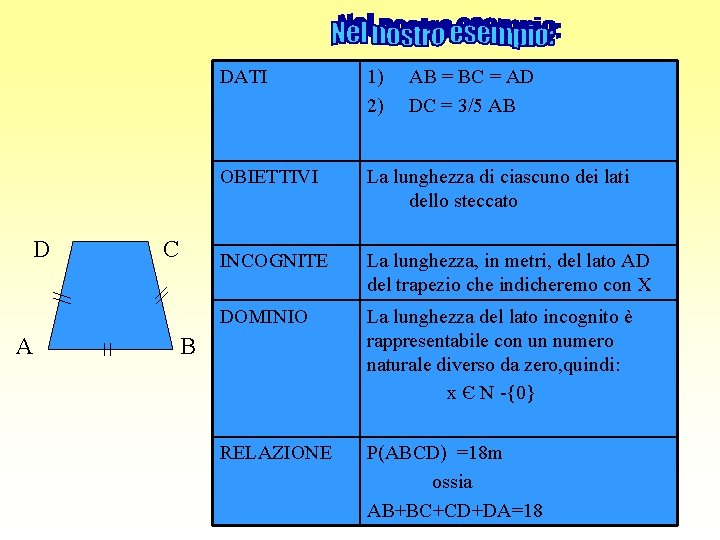
Una persona deve costruire uno steccato a forma di trapezio isoscele. Sapendo che la base maggiore è uguale a ciascuno dei lati obliqui, mentre la base minore è i 3/5 di quella maggiore e il perimetro è di 18 metri, calcolate quale sarà la lunghezza di ciascuno dei lati dello steccato.

Ricorda che, per la risoluzione di un problema, occorre individuare: Obiettivi Quali risultati dobbiamo ottenere? Dati Quali informazioni ci fornisce il testo del problema? Incognite Quali sono le grandezze di cui non conosciamo il valore? Dominio Con quale insieme numerico sono rappresentabili le grandezze indicate dalle incognite? Relazioni Di quali “risorse” (conoscenze teoriche, strumenti di calcolo)disponiamo per formalizzare le informazioni?

D A C DATI 1) 2) OBIETTIVI La lunghezza di ciascuno dei lati dello steccato INCOGNITE La lunghezza, in metri, del lato AD del trapezio che indicheremo con X DOMINIO La lunghezza del lato incognito è rappresentabile con un numero naturale diverso da zero, quindi: x Є N -{0} RELAZIONE P(ABCD) =18 m ossia AB+BC+CD+DA=18 B AB = BC = AD DC = 3/5 AB

FORMALIZZAZIONE LINGUAGGIO NATURALE LINGUAGGIO FORMALE La base maggiore è uguale a ciascuno dei lati obliqui; la loro misura sarà un certo numero di metri x la base minore è i 3/5 di quella maggiore Il perimetro é = di 18 metri 18

Quindi la relazione prima indicata diventa: Rappresenta una equazione di 1 grado nell’incognit ax

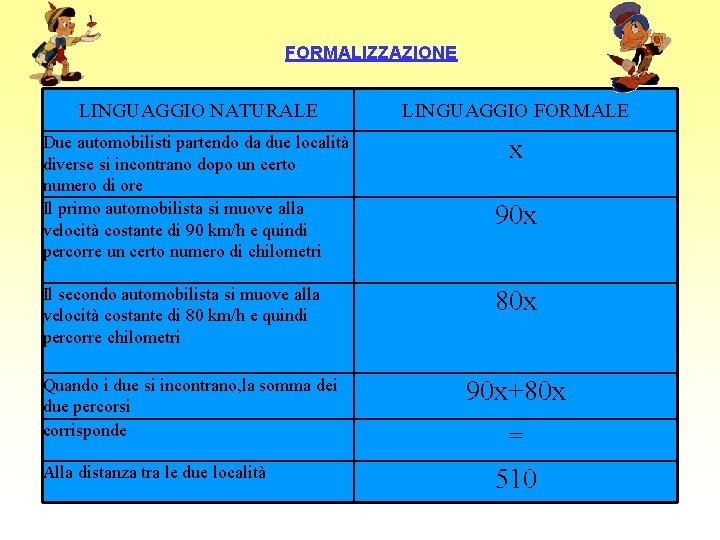
Reggio Calabria Napoli Due automobilisti partono da due diverse località, Reggio Calabria e Napoli, che distano fra di loro 510 km. Il primo viaggia alla velocità costante di 90 km/h, il secondo alla velocità costante di 80 km/h. Dopo quanto tempo si incontrano? E a quale distanza da Reggio Calabria? Provate a dare le vostre risposte: I due automobilisti si incontrano dopo…………. . Si trovano alla distanza di km……. da Reggio Calabria

Proviamo adesso a risolvere il problema con lo strumento “equazione” e dopo confrontiamo i risultati e soprattutto il modo di procedere. Ricordate che in Fisica il rapporto tra lo spazio, percorso da un mobile, e il tempo impiegato a percorrerlo, viene misurato da una grandezza chiamata velocità ed espresso in m/s o km/h. ? In formule: Da cui si ricavano facilmente, come vedrete dopo aver studiato le equazioni,

NEL NOSTRO PROBLEMA: 1. OBIETTIVI DATI INCOGNITE DOMINIO 2. a) b) c) Determinare dopo quanto tempo i due automobilisti si incontrano. Determinare a quale distanza da Reggio Calabria si incontrano. Distanza tra le due località : km 510 Velocità del primo automobilista: 90 km/h Velocità del secondo automobilista: 80 km/h Numero delle ore trascorse dalla partenza al momento in cui gli automobilisti si incontrano : x Le ore sono rappresentabili con un numero naturale diverso da zero, quindi: x Є N -{0}

FORMALIZZAZIONE LINGUAGGIO NATURALE LINGUAGGIO FORMALE Due automobilisti partendo da due località diverse si incontrano dopo un certo numero di ore Il primo automobilista si muove alla velocità costante di 90 km/h e quindi percorre un certo numero di chilometri x Il secondo automobilista si muove alla velocità costante di 80 km/h e quindi percorre chilometri Quando i due si incontrano, la somma dei due percorsi corrisponde Alla distanza tra le due località 90 x 80 x 90 x+80 x = 510

LA RELAZIONE : 90 x+80 x=510 COSTITUISCE IL MODELLO MATEMATICO del problema E’ una equazione di primo grado in una incognita!

Un’equazione è un’uguaglianza fra due espressioni algebriche risulta verificata solo per particolari valori attribuiti alla lettera x. Tali particolari valori costituiscono le soluzioni dell’equazione. Esempio: 2 x+1=7 2 x-6 = 0 è un’equazione e risulta verificata solo per il valore di x=3 (soluzione) Grado di un’equazione intera nella forma P(x)=0: È il grado del polinomio È di 1° perché il polinomio al primo membro è di 1°. Le due espressioni a sinistra e a destra del segno di uguaglianza si chiamano membri dell’equazione.

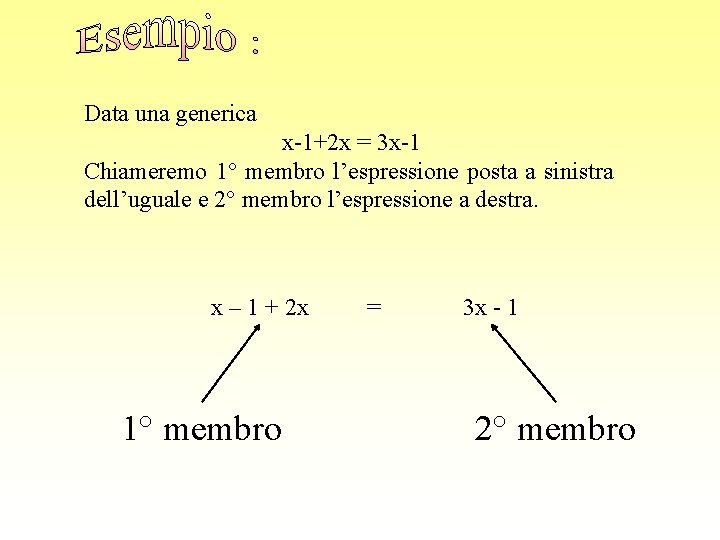
Data una generica x-1+2 x = 3 x-1 Chiameremo 1° membro l’espressione posta a sinistra dell’uguale e 2° membro l’espressione a destra. x – 1 + 2 x 1° membro = 3 x - 1 2° membro

I valori che rendono vera l’uguaglianza si chiamano soluzioni o radici dell’equazione. Si può anche dire che tali valori “verificano” l’equazione. Esempio: y-9=1 Ha come soluzione il valore 10, perché 10 -9=1. Diciamo che la soluzione è y=10. Risolvere un’equazione significa determinare tutte le sue soluzioni, cioè tutti i valori che verificano l’uguaglianza.

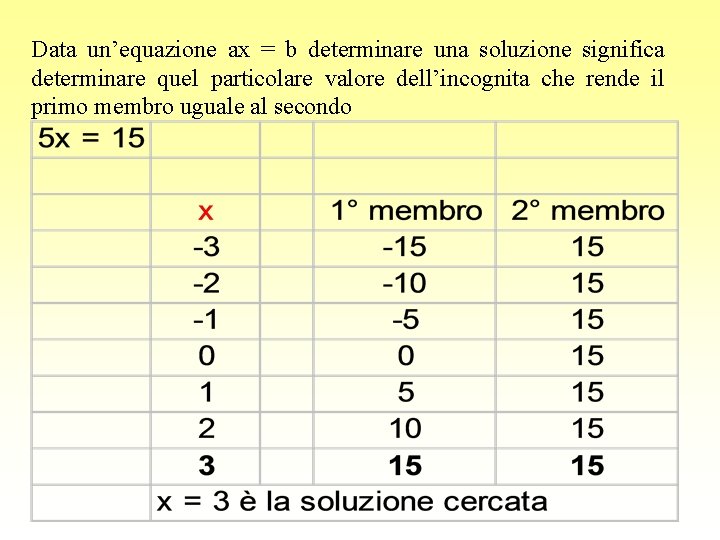
Data un’equazione ax = b determinare una soluzione significa determinare quel particolare valore dell’incognita che rende il primo membro uguale al secondo

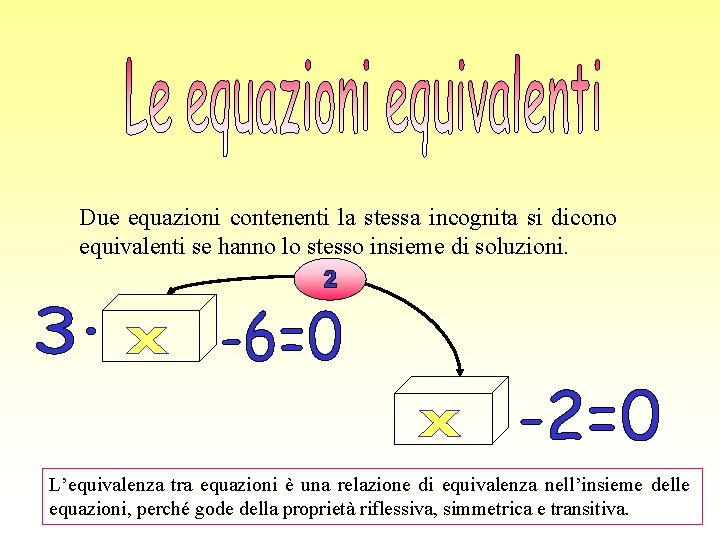
Due equazioni contenenti la stessa incognita si dicono equivalenti se hanno lo stesso insieme di soluzioni. L’equivalenza tra equazioni è una relazione di equivalenza nell’insieme delle equazioni, perché gode della proprietà riflessiva, simmetrica e transitiva.

Per risolvere un’equazione è necessario applicare un procedimento risolutivo, occorre cioè conoscere i metodi che consentono di trasformare un’assegnata equazione in una nuova equazione ad essa equivalente ma di forma più semplice. A tale scopo è necessario applicare due importanti teoremi detti principi di equivalenza. Si utilizzano per trasformare un’equazione in una equivalente, di solito più semplice

PRIMO PRINCIPIO DI EQUIVALENZA Se si aggiunge o si sottrae una stessa espressione letterale, contenente o no l’ incognita, per entrambi i membri, si ottiene un’equazione equivalente. Esempio: 8 x – 6 = 7 x + 4 ; x = 10 SECONDO PRINCIPIO DI EQUIVALENZA Se si moltiplicano o o si dividono entrambi i membri di un’equazione per uno stesso numero, diverso da 0, o per una stessa espressione letterale ( escludere i valori delle lettere che la annullano o che la rendono priva di significato), si ottiene un’equazione equivalente alla precedente. Esempio: 8 x = -16 ; x= -2 Applicando il 1° principio, aggiungiamo ambo i membri l’espressione: 6 – 7 x: Applicando il 2° principio, dividendo ambo i membri per 8 0: 8 x – 6 + 6 – 7 x = 7 x + 4 + 6 – 7 x x = 10 8 x : 8 = – 16 : 8 x=– 2

Ecco la soluzione del primo problema analizzato L’equazione risolvente era: ossia: cioé Per il secondo principio di equivalenza, moltiplicando ambedue i membri per 5, diventa 18 x = 90 e, dividendo ancora entrambi i membri per 18 si ottiene x= 5 quindi i lati dello steccato AB=BC=AD =5 metri, mentre il lato DC=3 metri.

LA RELAZIONE : 90 x+80 x=510 Ecco la soluzione del secondo problema analizzato Equivale a: 170 x=510 ( modello generale; ax=b) Da cui Dividendo ambedue i membri per 170 ( II principio di equivalenza) Si ottiene: E cioè: Ciò significa che gli automobilisti si incontrano dopo 3 ore dalla partenza Sostituendo poi quest’ultimo dato nella formula già vista L’incontro avviene a 270 km da Reggio Calabria

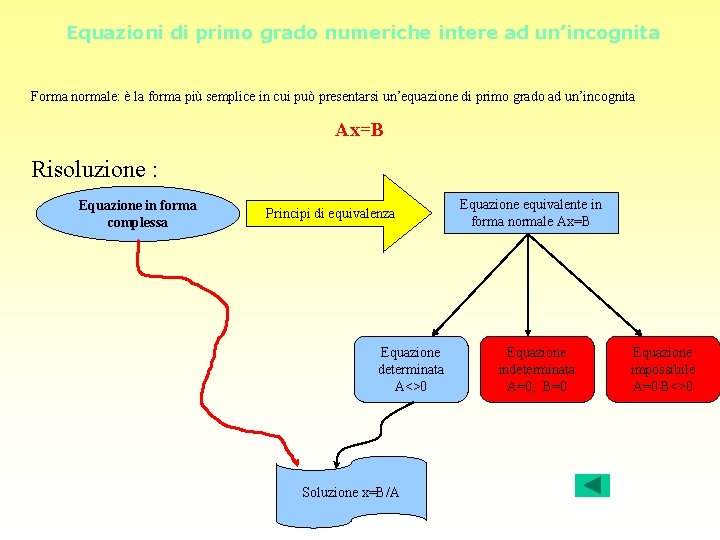
Equazioni di primo grado numeriche intere ad un’incognita Forma normale: è la forma più semplice in cui può presentarsi un’equazione di primo grado ad un’incognita Ax=B Risoluzione : Equazione in forma complessa Principi di equivalenza Equazione determinata A<>0 Soluzione x=B/A Equazione equivalente in forma normale Ax=B Equazione indeterminata A=0; B=0 Equazione impossibile A=0 B<>0

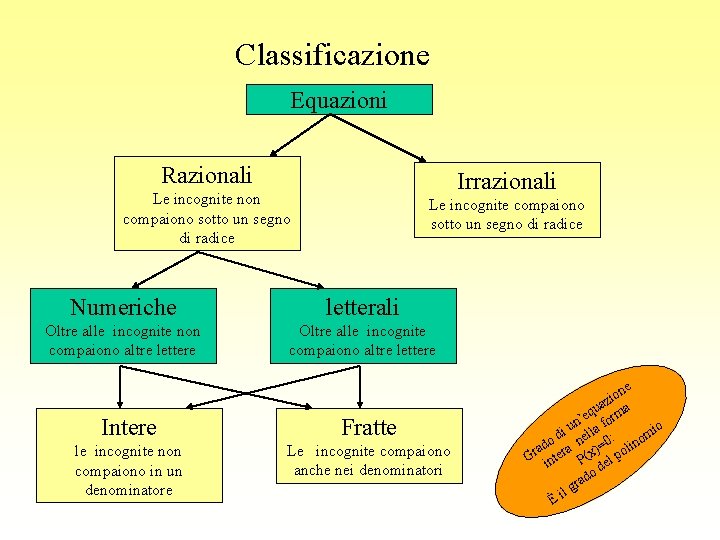
Le equazioni si classificano in base: alla posizione dell’incognita ai coefficienti intere fratte numeriche letterali determinate all’ esistenza di soluzioni indeterminate impossibili

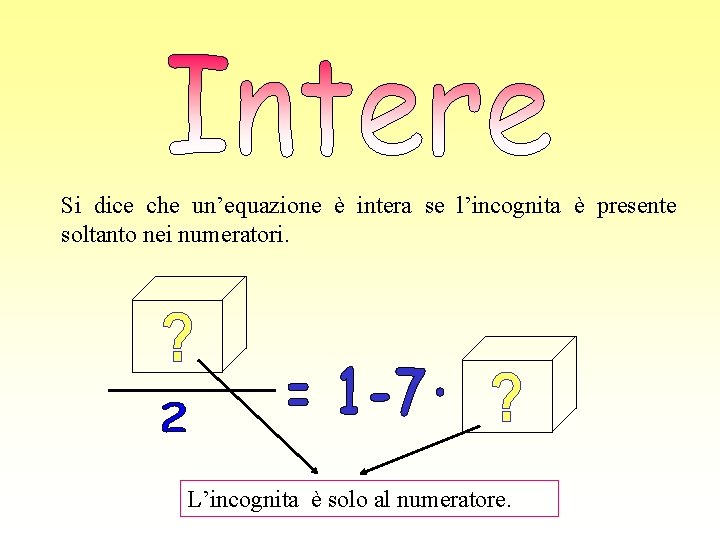
Si dice che un’equazione è intera se l’incognita è presente soltanto nei numeratori. L’incognita è solo al numeratore.

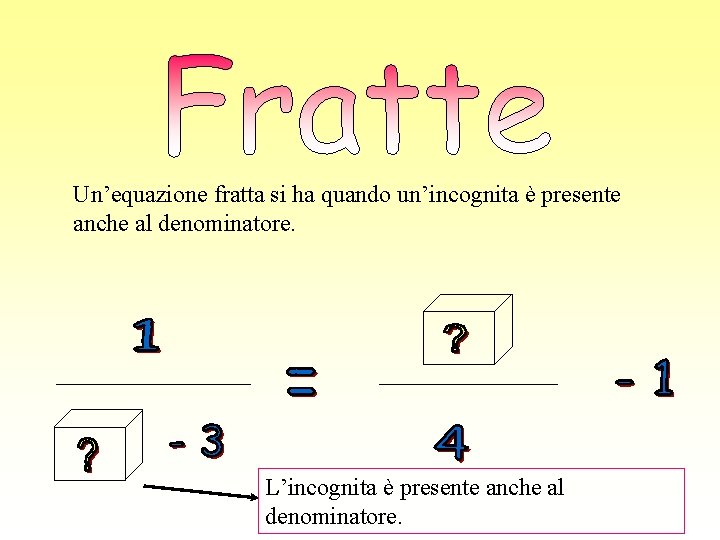
Un’equazione fratta si ha quando un’incognita è presente anche al denominatore. L’incognita è presente anche al denominatore.

Quando si risolve un’equazione fratta, bisogna fare attenzione al dominio, cioè all’insieme numerico dell’incognita x ! Ad esempio, nell’equazione fratta Il dominio è rappresentato da R-{0, -1}, cioé dall’insieme dei numeri reali tranne 0 e -1. Ciò significa che la x e quindi la soluzione non potrà mai assumere valore 0 o -1. I valori 0 e -1 sostituiti nell’equazione alla x, renderebbero i denominatori nulli, quindi le frazioni senza significato e l’equazione impossibile!

Abbiamo delle equazioni numeriche quando tutti i coefficienti sono numeri. Sono tutti numeri

In un’equazione letterale nei coefficienti sono presenti anche le lettere Contiene delle lettere

Anche le equazioni letterali vanno ridotte alla forma normale ax =b Ho capito! Le equazioni letterali, sono quelle che si devono discutere! Le loro soluzioni dipendono dal valore del coefficiente della incognita x. Forse è meglio rivedere la slide n. 22! Nelle equazioni letterali compaiono oltre alla incognita x altre lettere che possono assumere valore diverso e dare così luogo ad equazioni numeriche di tipo diverso.

Un’equazione è determinata se ha un numero finito di soluzioni È determinata in quanto ha una soluzione:

Se un’equazione ha infinite soluzioni è detta indeterminata È indeterminata perché possiede infiniti valori di x, al variare di y e viceversa: Esempi: Se y=0 allora x=1; Se y =1 allora x=0; Se x=3 allora y=-2. . ecc.

Questo è un altro caso di equazione indeterminata in quanto NB: la soluzione di questa equazione è data da qualsiasi numero reale, quindi tale equazione ha infinite soluzioni: tutti i numeri reali.

Un’equazione che non ha soluzioni si chiama impossibile. Non esiste alcun valore di x che renda vera l’uguaglianza, per questo si dice che è una equazione impossibile.

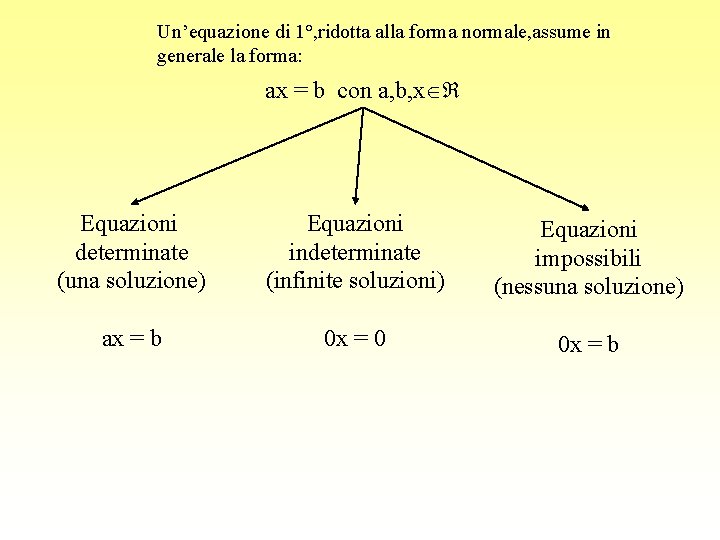
Un’equazione di 1°, ridotta alla forma normale, assume in generale la forma: ax = b con a, b, x Equazioni determinate (una soluzione) Equazioni indeterminate (infinite soluzioni) Equazioni impossibili (nessuna soluzione) ax = b 0 x = 0 0 x = b

Classificazione Equazioni Razionali Irrazionali Le incognite non compaiono sotto un segno di radice Le incognite compaiono sotto un segno di radice Numeriche letterali Oltre alle incognite non compaiono altre lettere Oltre alle incognite compaiono altre lettere Intere Fratte le incognite non compaiono in un denominatore Le incognite compaiono anche nei denominatori ne o i z ua ma q r ’e un lla fo io i m d e : o o n ad era x)=0 polin r G int P( el od d ra lg i È
 Equazioni con le frazioni
Equazioni con le frazioni Equazioni razionali fratte
Equazioni razionali fratte Come trasformare un numero decimale in frazione
Come trasformare un numero decimale in frazione Mogans cevicheria
Mogans cevicheria Calcolare frazione di un numero
Calcolare frazione di un numero Problemi frazioni algebriche
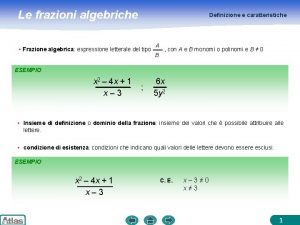
Problemi frazioni algebriche Come semplificare le frazioni algebriche
Come semplificare le frazioni algebriche Riduzione al minimo comune denominatore
Riduzione al minimo comune denominatore Proporzioni rinascimento
Proporzioni rinascimento Addizione tra frazioni
Addizione tra frazioni Proporzioni multiple
Proporzioni multiple Calcoli sopra cento inversi
Calcoli sopra cento inversi Proporzioni in cucina
Proporzioni in cucina Proporzioni
Proporzioni Proporzione continua come si risolve
Proporzione continua come si risolve Calcoli sotto cento inversi
Calcoli sotto cento inversi Scale di proporzione esercizi
Scale di proporzione esercizi Rapporto massa grassa massa magra
Rapporto massa grassa massa magra Come mi vedo io
Come mi vedo io He-y, come on ou-t meaning
He-y, come on ou-t meaning Come mi chiamo io
Come mi chiamo io Come in come in and sit down
Come in come in and sit down Get in touch with god turn your radio on
Get in touch with god turn your radio on Come thou fount come thou king
Come thou fount come thou king Come lord jesus come and be born in our hearts lyrics
Come lord jesus come and be born in our hearts lyrics Come in come in and sit down
Come in come in and sit down Come mi chiamo come mi chiamo
Come mi chiamo come mi chiamo Tear past tense
Tear past tense Softly and tenderly jesus is calling
Softly and tenderly jesus is calling Come holy ghost lyrics
Come holy ghost lyrics Blow simple past tense
Blow simple past tense E m m a n u e l
E m m a n u e l Terza equazione di maxwell
Terza equazione di maxwell Quarta equazione di maxwell
Quarta equazione di maxwell Equazioni maxwell
Equazioni maxwell Metodo di eulero
Metodo di eulero