Numerical Integration Jim Van Verth Insomniac Games jimessentialmath

Numerical Integration Jim Van Verth Insomniac Games jim@essentialmath. com

Talk Summary > Going to talk about: Euler’s method subject to errors > Implicit methods help, but complicated > Verlet methods help, but velocity out of step > Symplectic methods can be good for both >

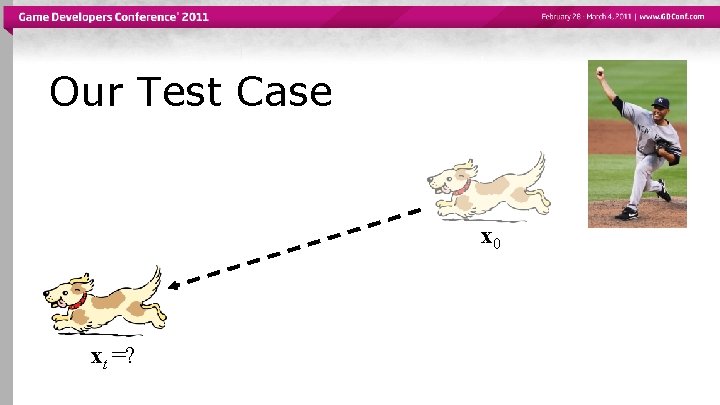
Our Test Case

Our Test Case

Our Test Case x 0 xt =?

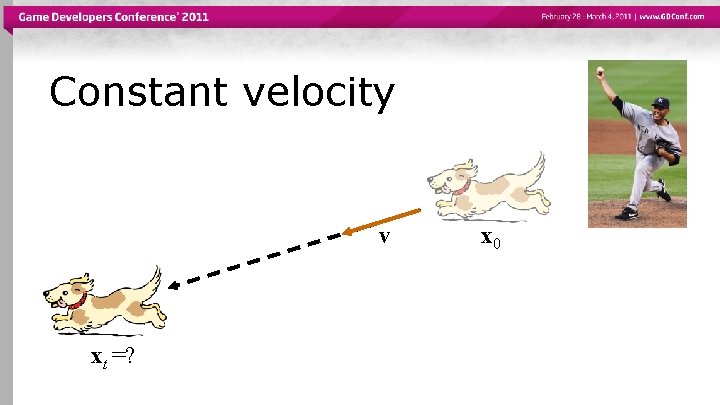
Constant velocity v xt =? x 0

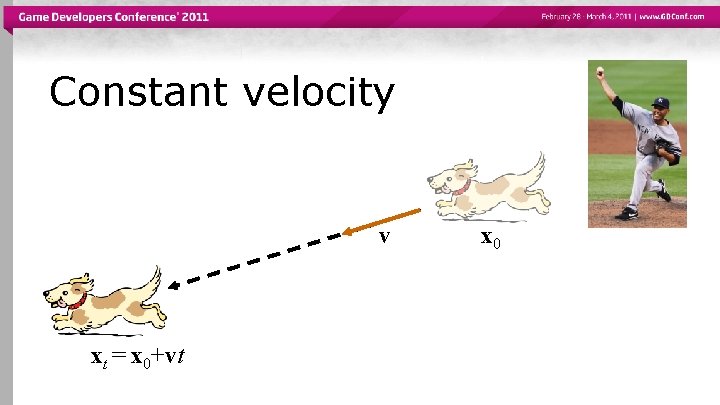
Constant velocity v xt = x 0+vt x 0

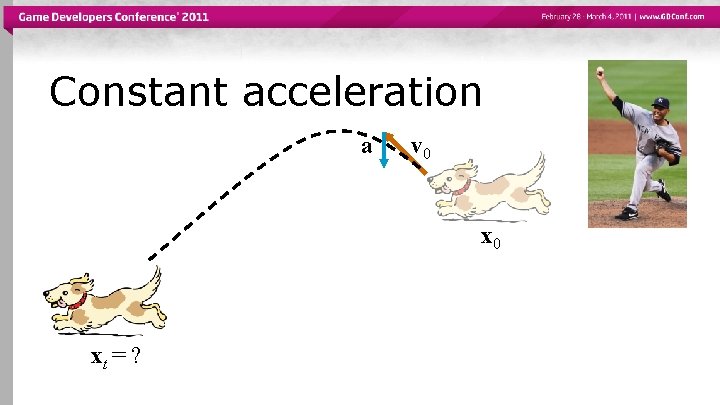
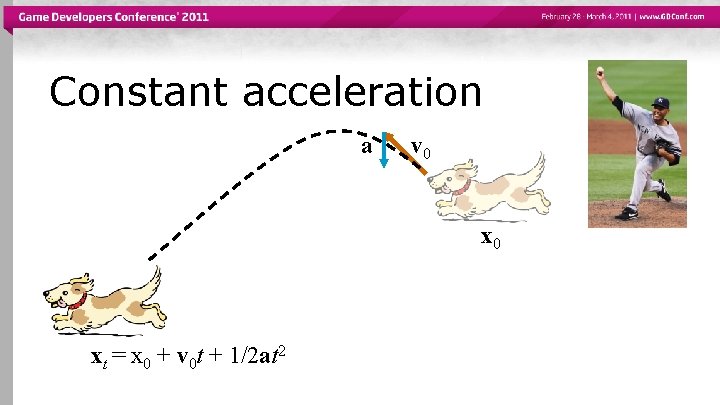
Constant acceleration a v 0 xt = ?

Constant acceleration a v 0 xt = ?

Constant acceleration a v 0 xt = x 0 + v 0 t + 1/2 at 2

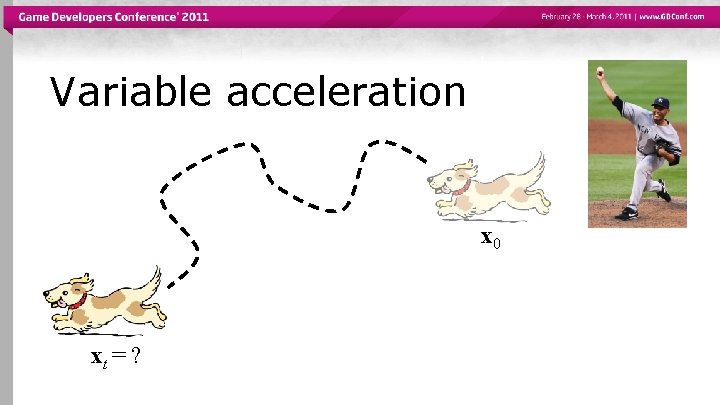
Variable acceleration x 0 xt = ?

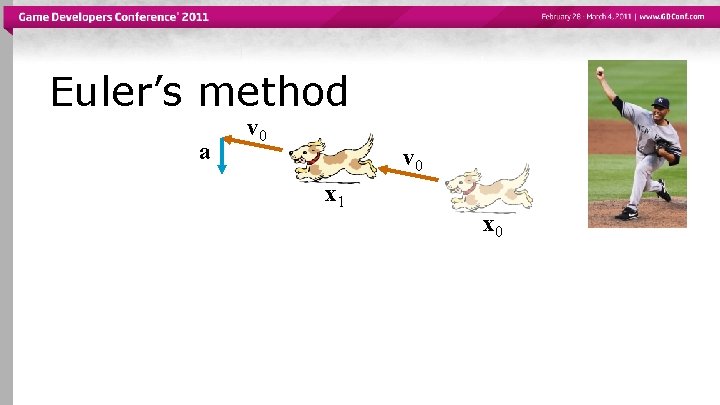
Euler’s method v 0 x 0

Euler’s method v 0 x 1 x 0

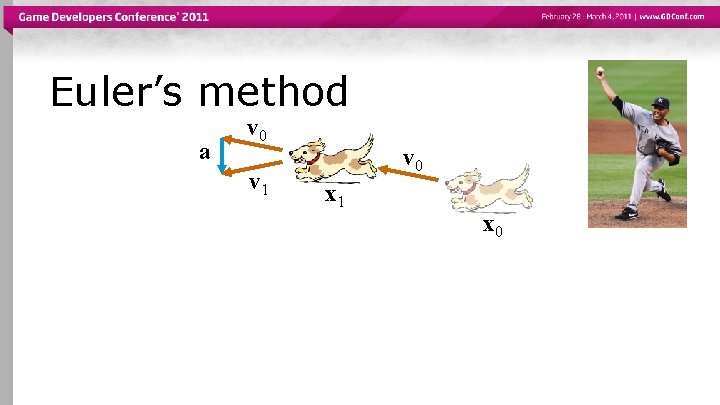
Euler’s method a v 0 x 1 x 0

Euler’s method a v 0 v 1 v 0 x 1 x 0

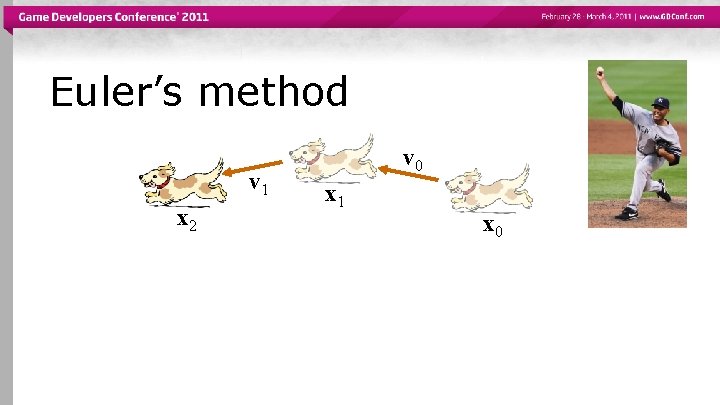
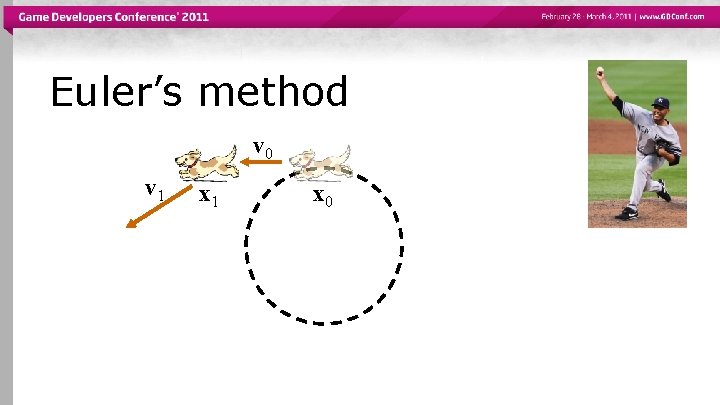
Euler’s method v 1 v 0 x 1 x 0

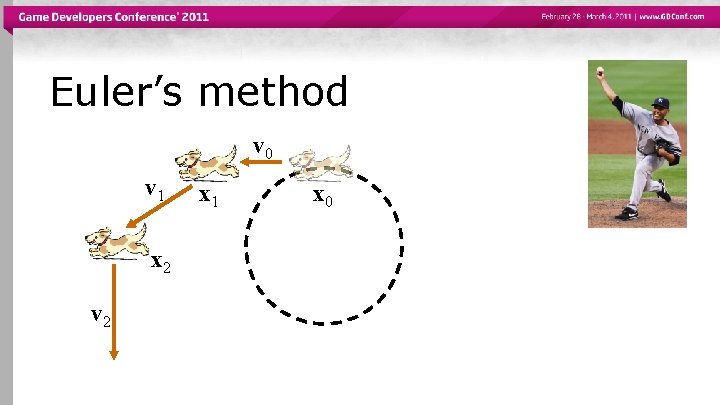
Euler’s method v 1 x 2 v 0 x 1 x 0

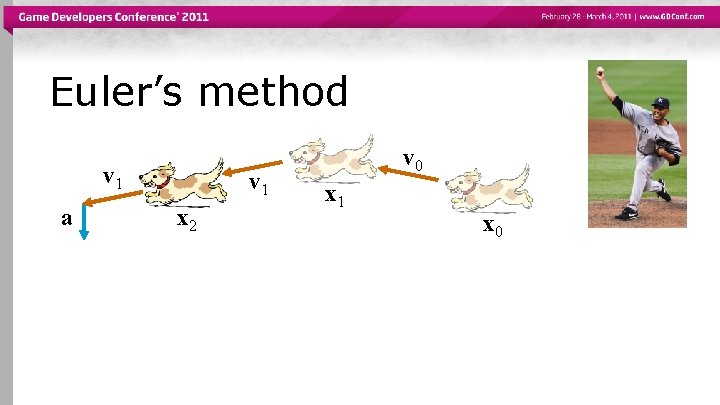
Euler’s method v 1 a v 1 x 2 v 0 x 1 x 0

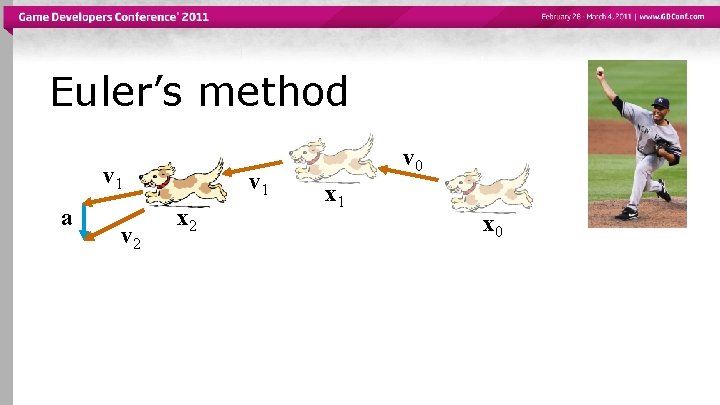
Euler’s method v 1 a v 2 v 1 x 2 v 0 x 1 x 0

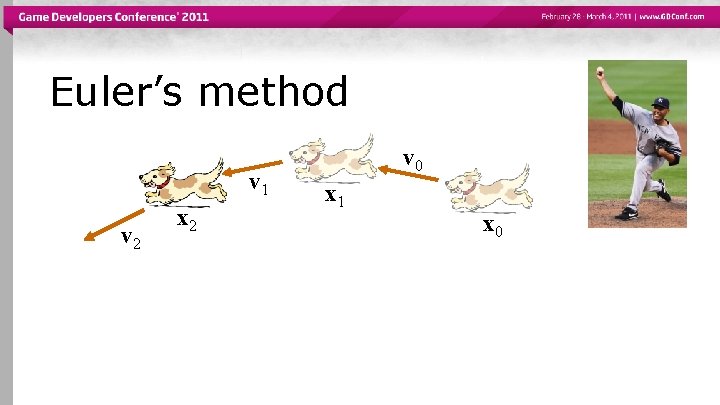
Euler’s method v 1 v 2 x 2 v 0 x 1 x 0

Euler’s method v 1 v 2 x 2 v 0 x 1 x 0

Euler’s method v 0 x 0 a 0

Euler’s method v 0 x 1 x 0 a 0

Euler’s method v 0 a 0 v 0 x 1 x 0

Euler’s method v 0 a 0 v 1 v 0 x 1 x 0

Euler’s method v 0 v 1 x 0

Euler’s method v 0 v 1 x 2 v 2 x 1 x 0

Euler’s method v 0 x 0 v 1 x 1

Euler Okay for non-oscillating systems > Explodes with oscillating systems > Adds energy! Very bad! >

Runge-Kutta methods v 0 x 0

Runge-Kutta methods v 0. 5 x 0

Runge-Kutta methods v 0. 5 x 0

Runge-Kutta methods v 0. 5 x 1 x 0

Runge-Kutta methods v 0 x 0

Runge-Kutta 4 Very stable and accurate > Conserves energy well > But expensive: four evaluations of derivative >

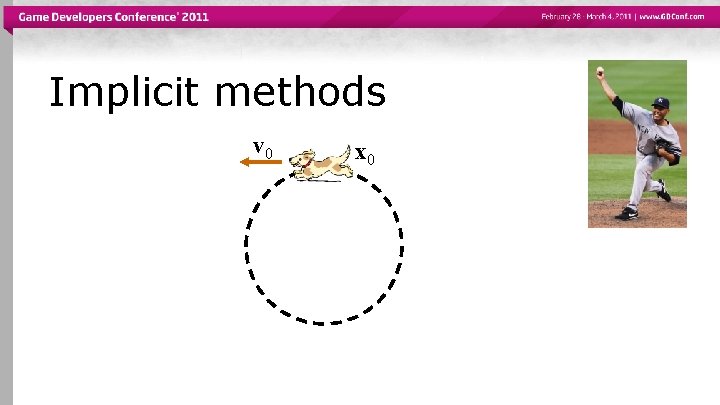
Implicit methods v 0 x 0

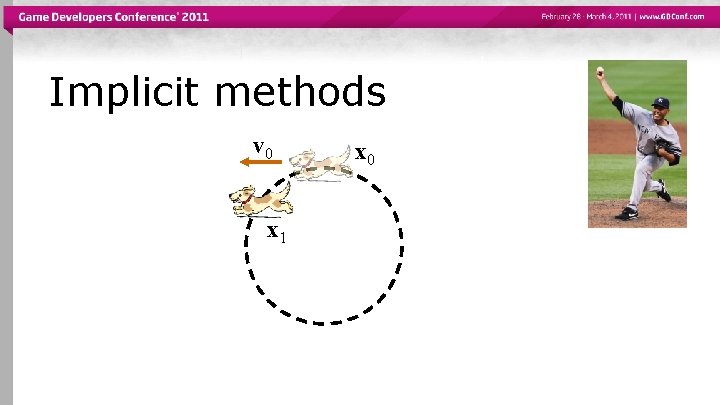
Implicit methods v 0 x 1 x 0

Implicit methods v 0 v 1 x 0

Implicit methods v 0 x 0 v 1

Implicit methods v 0 x 0 v 1 x 1

Implicit methods v 0 x 0 v 1 x 1

Implicit methods v 0 v 1 x 0

Implicit methods v 0 x 0 v 1 x 1

Backward Euler Not easy to get implicit values > More expensive than Euler > > But tends to converge: better but not ideal

Verlet x 0 x-1

Verlet x 0 x-1

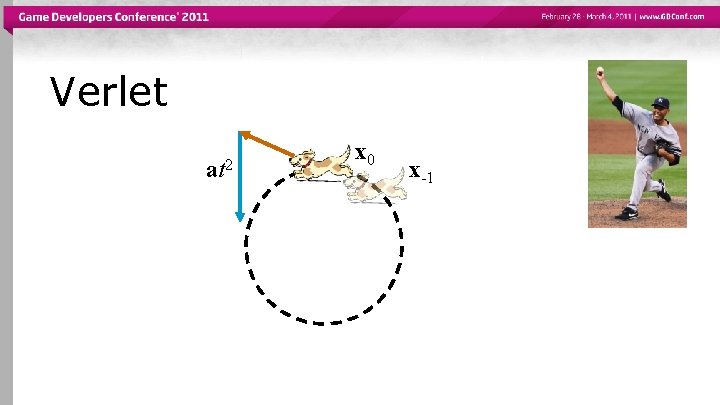
Verlet at 2 x 0 x-1

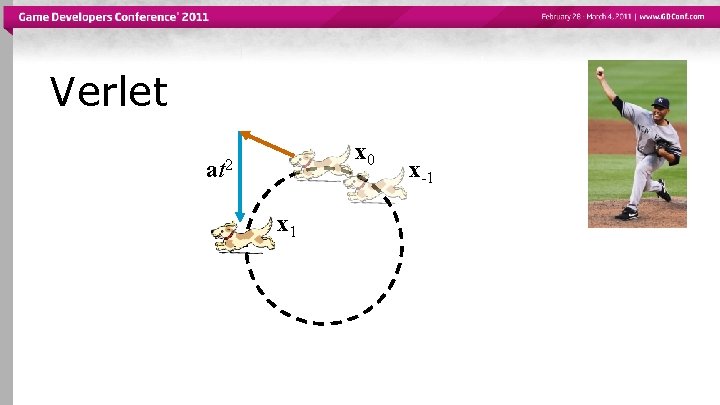
Verlet x 0 at 2 x 1 x-1

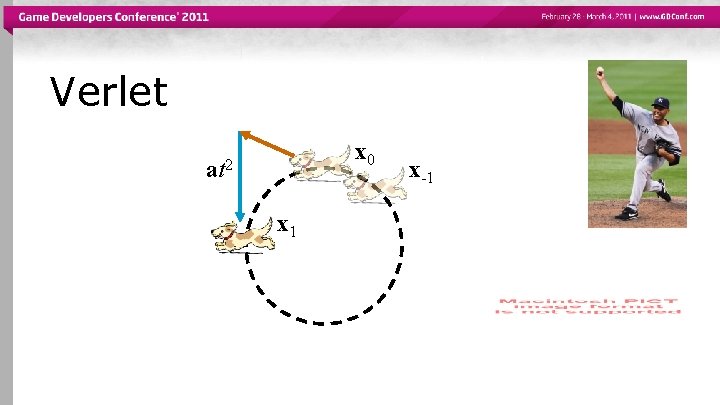
Verlet x 0 at 2 x 1 x-1

Verlet > Leapfrog Verlet > Velocity Verlet

Verlet Very stable > Cheap > > Not too bad, but have estimated velocity

Symplectic Euler v 0 x 0 a 0

Symplectic Euler v 0 a 0 x 0 v 1

Symplectic Euler x 0 v 1

Symplectic Euler x 0 v 1

Symplectic Euler

Symplectic Euler > Cheap and stable! > Not as accurate as RK 4

Symplectic Euler > Cheap and stable! > Not as accurate as RK 4 - but hey, it’s a game

Demo Time

Which To Use? > > > With simple forces, standard Euler might be okay But constraints, springs, etc. require stability Recommendation: Symplectic Euler > > > Generally stable Simple to compute (just swap velocity and position terms) More complex integrators available if you need them -see references

References > > > Burden, Richard L. and J. Douglas Faires, Numerical Analysis, PWS Publishing Company, Boston, MA, 1993. Witken, Andrew, David Baraff, Michael Kass, SIGGRAPH Course Notes, Physically Based Modelling, SIGGRAPH 2002. Eberly, David, Game Physics, Morgan Kaufmann, 2003.

References Hairer, et al, “Geometric Numerical Integration Illustrated by the Störmer/Verlet method, ” Acta Numerica (2003), pp 1 -51. > Robert Bridson, Notes from CPSC 533 d: Animation Physics, University of BC. >