Numerical Integration 1 Introduction to Numerical Integration p

Numerical Integration 1

Introduction to Numerical Integration p p p Definitions Upper and Lower Sums Trapezoid Method (Newton-Cotes Methods) 2

Integration Indefinite Integrals Definite Integrals Indefinite Integrals of a function are functions that differ from each other by a constant. Definite Integrals are numbers. 3

Fundamental Theorem of Calculus 4

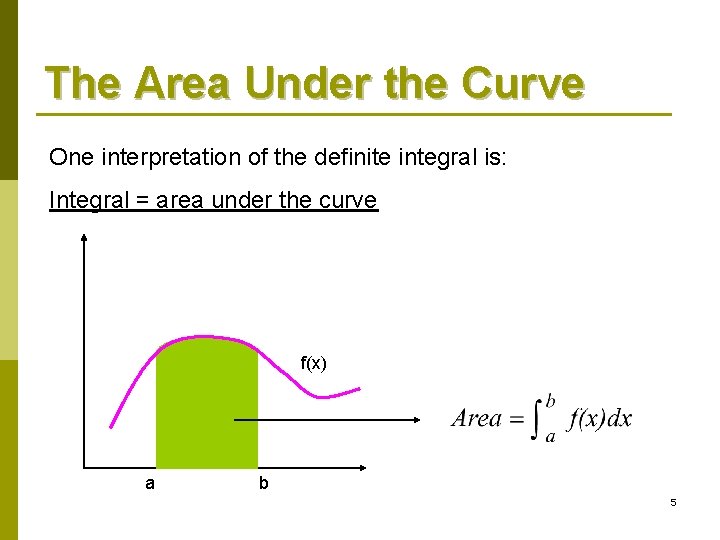
The Area Under the Curve One interpretation of the definite integral is: Integral = area under the curve f(x) a b 5

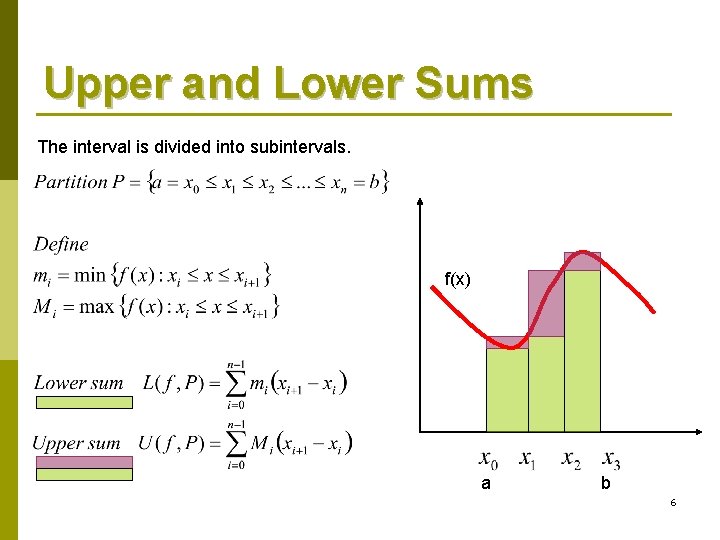
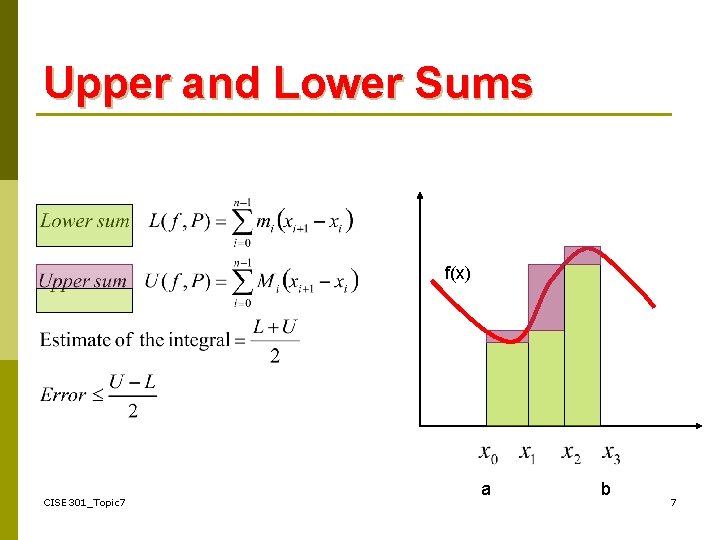
Upper and Lower Sums The interval is divided into subintervals. f(x) a b 6

Upper and Lower Sums f(x) CISE 301_Topic 7 a b 7

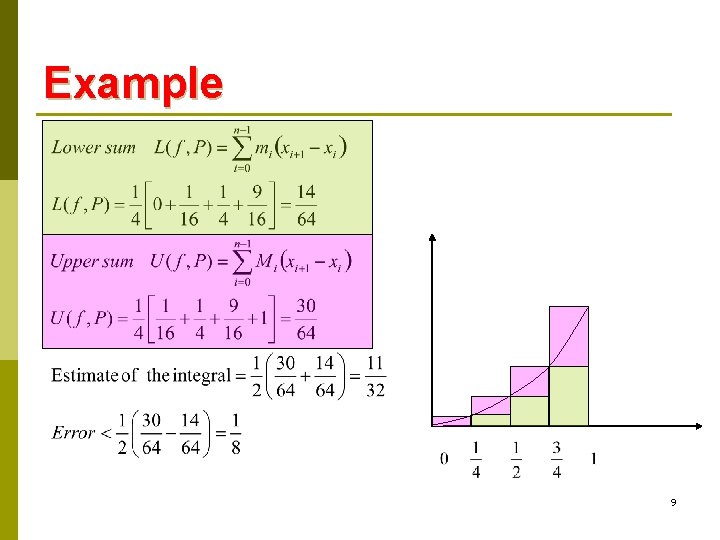
Example 8

Example 9

Upper and Lower Sums • Estimates based on Upper and Lower Sums are easy to obtain for monotonic functions (always increasing or always decreasing). • For non-monotonic functions, finding maximum and minimum of the function can be difficult and other methods can be more attractive. 10

Newton-Cotes Methods In Newton-Cote Methods, the function is approximated by a polynomial of order n. p Computing the integral of a polynomial is easy. p 11

Newton-Cotes Methods n Trapezoid Method (First Order Polynomials are used) n Simpson 1/3 Rule (Second Order Polynomials are used) 12

Trapezoid Method p p Derivation-One Interval Multiple Application Rule Estimating the Error Recursive Trapezoid Method 13

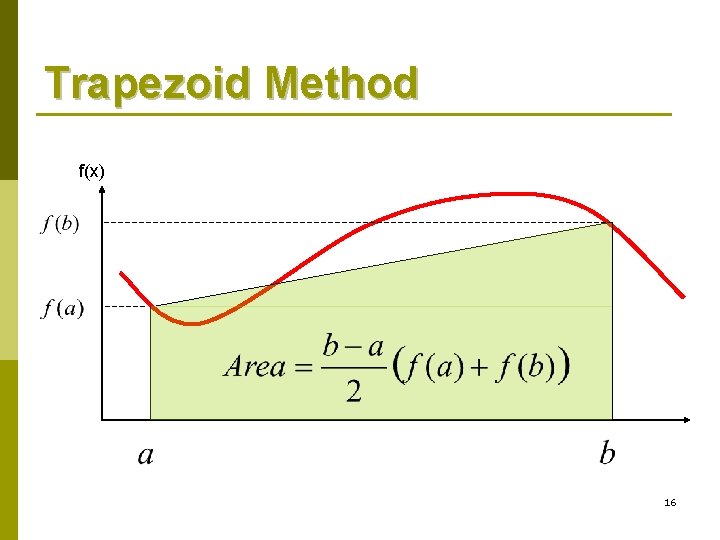
Trapezoid Method f(x) 14

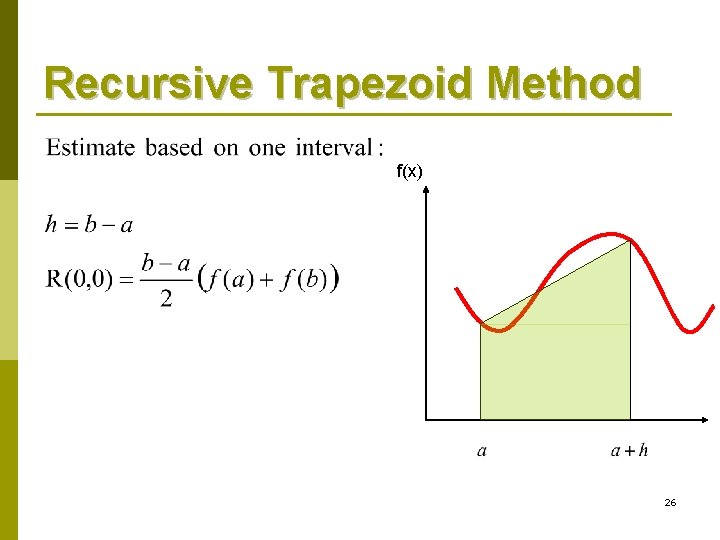
Trapezoid Method Derivation-One Interval 15

Trapezoid Method f(x) 16

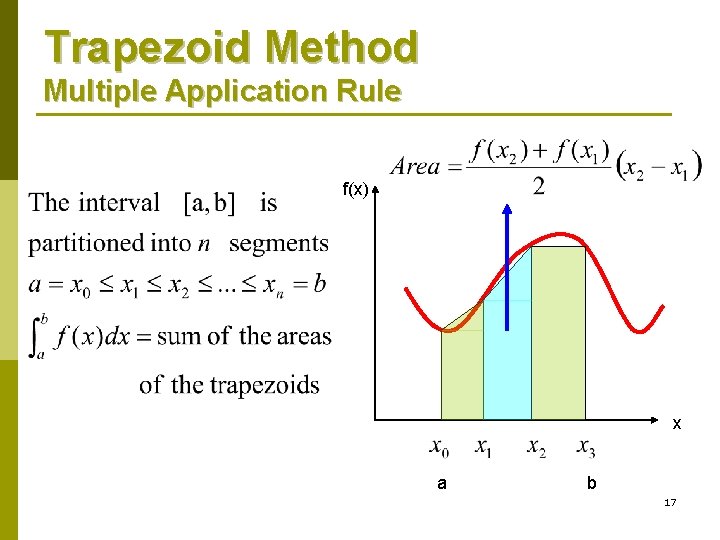
Trapezoid Method Multiple Application Rule f(x) x a b 17

Trapezoid Method General Formula and Special Case 18

Example Given a tabulated values of the velocity of an object. Time (s) 0. 0 1. 0 2. 0 3. 0 Velocity (m/s) 0. 0 10 12 14 Obtain an estimate of the distance traveled in the interval [0, 3]. Distance = integral of the velocity 19

Example 1 Time (s) 0. 0 1. 0 2. 0 3. 0 Velocity (m/s) 0. 0 10 12 14 20

Error in estimating the integral Theorem CISE 301_Topic 7 21

Estimating the Error For Trapezoid Method 22

Example 23

Example x 1. 0 1. 5 2. 0 2. 5 3. 0 f(x) 2. 1 3. 2 3. 4 2. 8 2. 7 24

Example x 1. 0 1. 5 2. 0 2. 5 3. 0 f(x) 2. 1 3. 2 3. 4 2. 8 2. 7 25

Recursive Trapezoid Method f(x) 26

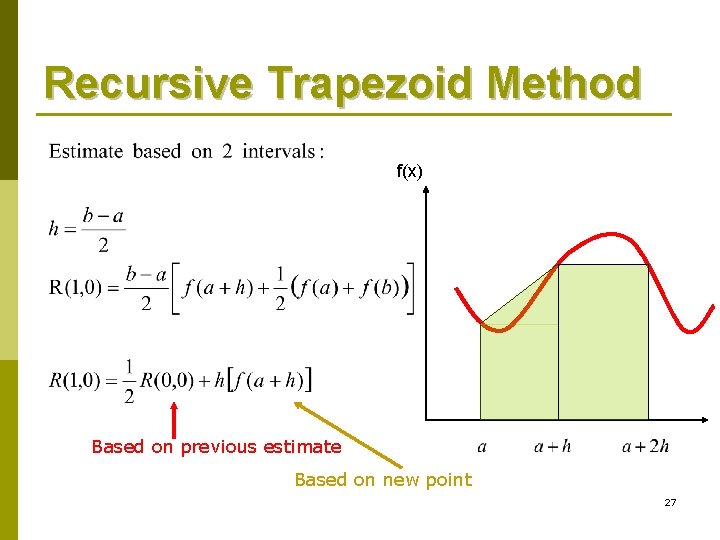
Recursive Trapezoid Method f(x) Based on previous estimate Based on new point 27

Recursive Trapezoid Method f(x) Based on previous estimate Based on new points 28

Recursive Trapezoid Method Formulas 29

Recursive Trapezoid Method 30

Example on Recursive Trapezoid n h R(n, 0) 0 (b-a)= /2 ( /4)[sin(0) + sin( /2)]=0. 785398 1 (b-a)/2= /4 R(0, 0)/2 + ( /4) sin( /4) = 0. 948059 2 (b-a)/4= /8 R(1, 0)/2 + ( /8)[sin( /8)+sin(3 /8)] = 0. 987116 3 (b-a)/8= /16 R(2, 0)/2 + ( /16)[sin( /16)+sin(3 /16)+sin(5 /16)+ sin(7 /16)] = 0. 996785 Estimated Error = |R(3, 0) – R(2, 0)| = 0. 009669 31

Advantages of Recursive Trapezoid: p Gives the same answer as the standard Trapezoid method. p Makes use of the available information to reduce the computation time. p Useful if the number of iterations is not known in advance. 32