Numerical Methods Numerical Differentiation and Integration Gauss Quadrature





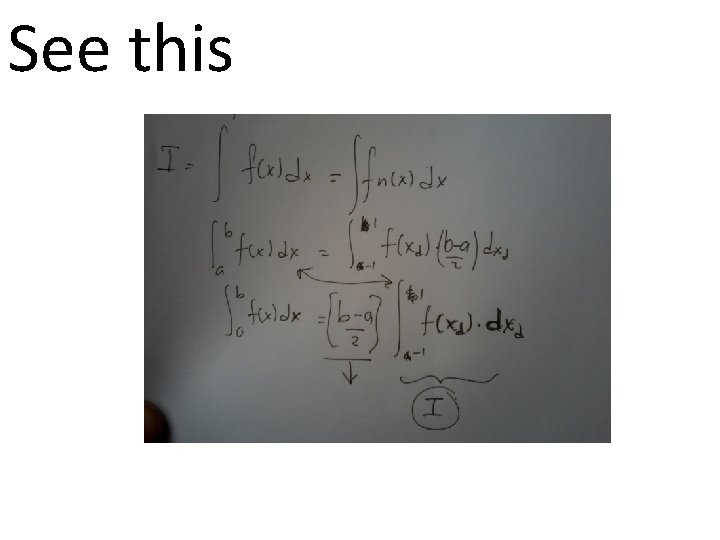
- Slides: 11

Numerical Methods Numerical Differentiation and Integration: Gauss Quadrature

The need for Gauss Quadrature Evaluating integrals are common in engineering problems. Sometimes, it is difficult to evaluate complex integrals. Therefore, techniques are devised in order to simplify these.

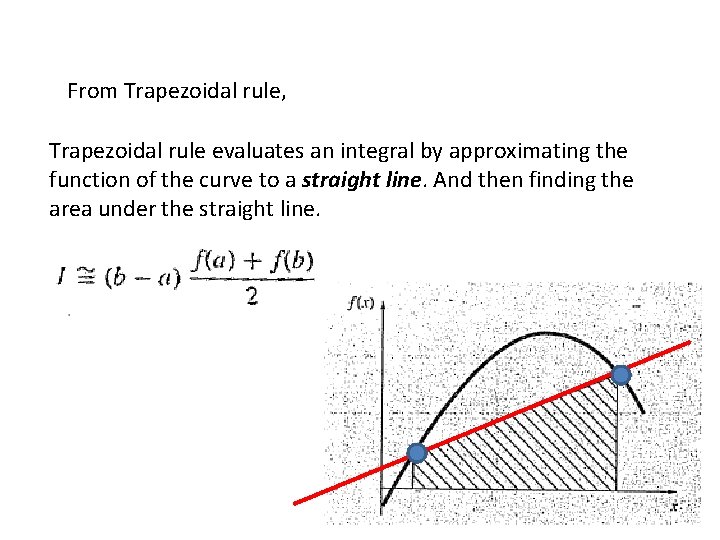
From Trapezoidal rule, Trapezoidal rule evaluates an integral by approximating the function of the curve to a straight line. And then finding the area under the straight line.

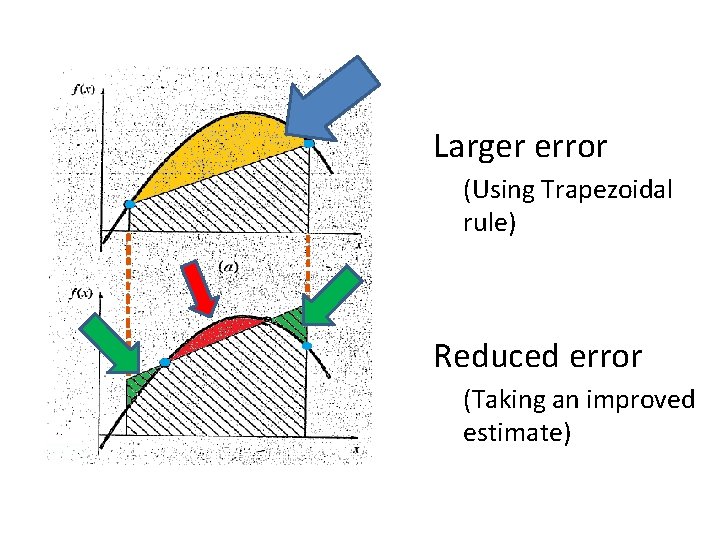
Larger error (Using Trapezoidal rule) Reduced error (Taking an improved estimate)

Method of Undetermined Coefficients Constant function Linear function Quadratic function Cubic function

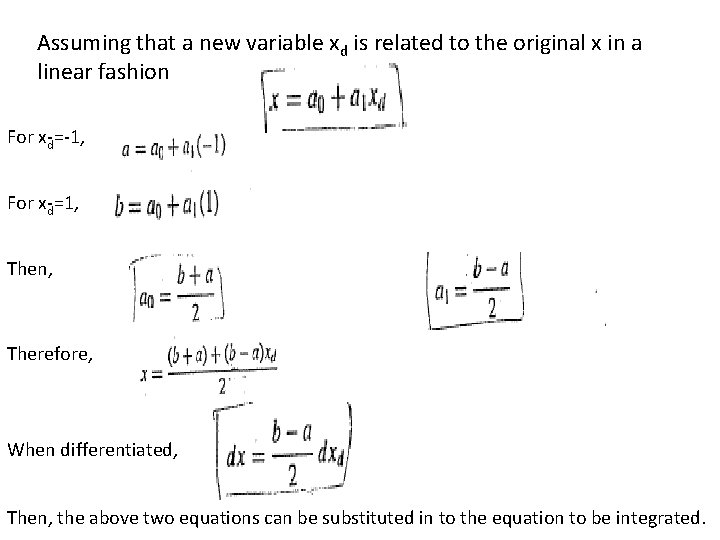
Assuming that a new variable xd is related to the original x in a linear fashion For x d= 1, For x d=1, Then, Therefore, When differentiated, Then, the above two equations can be substituted in to the equation to be integrated.

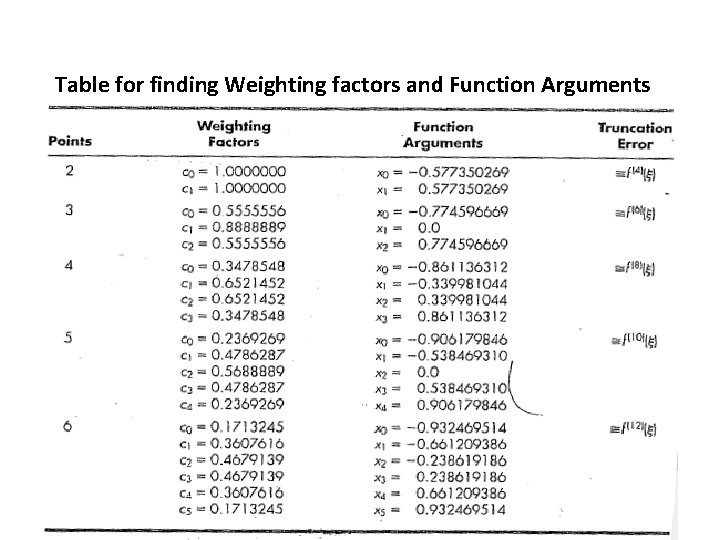
Table for finding Weighting factors and Function Arguments

Example 1: Use three-point formula to evaluate it. Solution: Given: a=-1 and b=1; f(x) = x+3 x 2+x 5 From table for three points, C 0=0. 5555556 C 1=0. 8888889 C 2=0. 5555556 X 0=-0. 774596669 X 1=0 X 2=0. 774596669 I=C 0 f(X 0) +C 1 f(X 1) +C 2 f(X 2) f (X 0)=. 7465 f(X 1)=0 f(X 2)=2. 8537762 I=[0. 5555556*. 7465+. 8888889*0+0. 5555556*2. 8537762]=2. 001

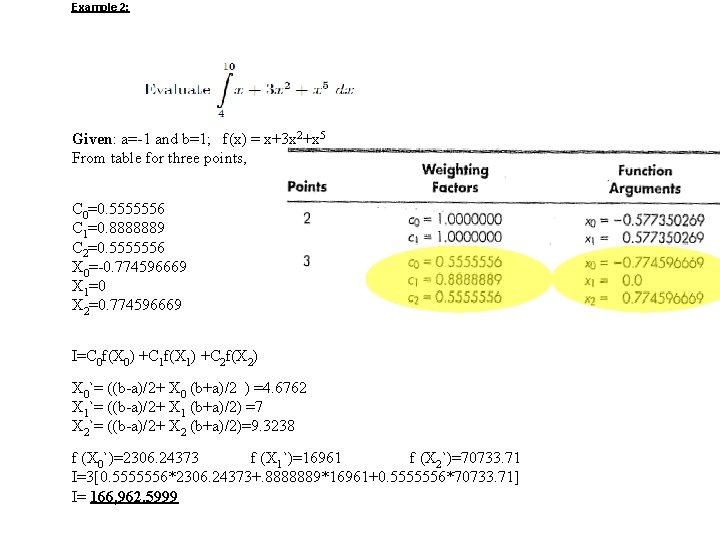
Example 2: Given: a=-1 and b=1; f(x) = x+3 x 2+x 5 From table for three points, C 0=0. 5555556 C 1=0. 8888889 C 2=0. 5555556 X 0=-0. 774596669 X 1=0 X 2=0. 774596669 I=C 0 f(X 0) +C 1 f(X 1) +C 2 f(X 2) X 0`= ((b-a)/2+ X 0 (b+a)/2 ) =4. 6762 X 1`= ((b-a)/2+ X 1 (b+a)/2) =7 X 2`= ((b-a)/2+ X 2 (b+a)/2)=9. 3238 f (X 0`)=2306. 24373 f (X 1`)=16961 f (X 2`)=70733. 71 I=3[0. 5555556*2306. 24373+. 8888889*16961+0. 5555556*70733. 71] I= 166, 962. 5999

Error Analysis for Gauss Quadrature
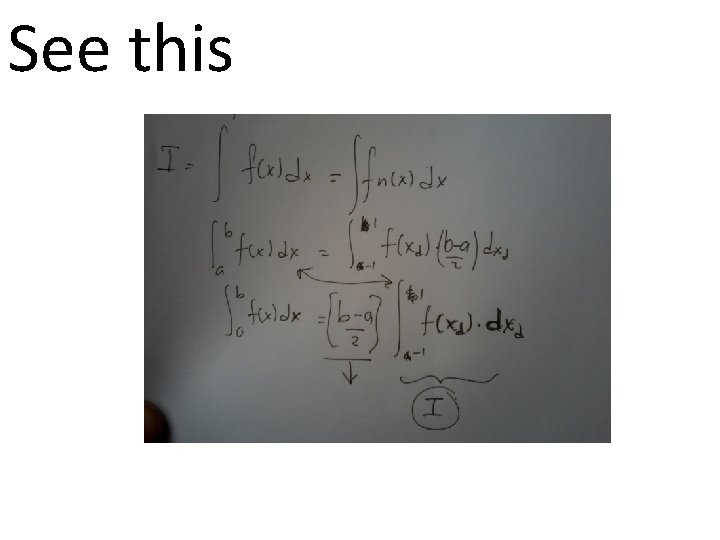
See this




















