Numerical Computation and Optimization Numerical Integration Gauss Quadrature

Numerical Computation and Optimization Numerical Integration Gauss Quadrature Rule By Assist Prof. Dr. Ahmed Jabbar

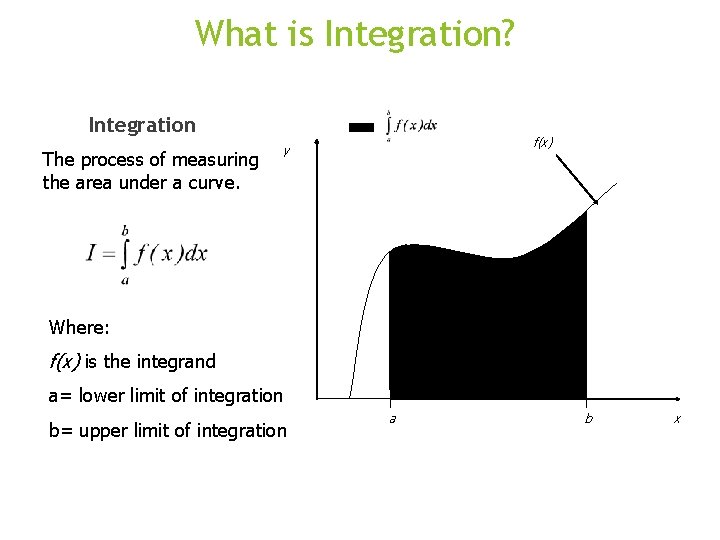
What is Integration? Integration The process of measuring the area under a curve. f(x) y Where: f(x) is the integrand a= lower limit of integration b= upper limit of integration a b x

Two-Point Gaussian Quadrature Rule

Basis of the Gaussian Quadrature Rule Previously, the Trapezoidal Rule was developed by the method of undetermined coefficients. The result of that development is summarized below.

Basis of the Gaussian Quadrature Rule The two-point Gauss Quadrature Rule is an extension of the Trapezoidal Rule approximation where the arguments of the function are not predetermined as a and b but as unknowns x 1 and x 2. In the two-point Gauss Quadrature Rule, the integral is approximated as

Basis of the Gaussian Quadrature Rule The four unknowns x 1, x 2, c 1 and c 2 are found by assuming that the formula gives exact results for integrating a general third order polynomial, Hence

Basis of the Gaussian Quadrature Rule It follows that Equating Equations the two previous two expressions yield

Basis of the Gaussian Quadrature Rule Since the constants a 0, a 1, a 2, a 3 are arbitrary

Basis of Gauss Quadrature The previous four simultaneous nonlinear Equations have only one acceptable solution,

Basis of Gauss Quadrature Hence Two-Point Gaussian Quadrature Rule

Higher Point Gaussian Quadrature Formulas

Higher Point Gaussian Quadrature Formulas is called the three-point Gauss Quadrature Rule. The coefficients c 1, c 2, and c 3, and the functional arguments x 1, x 2, and x 3 are calculated by assuming the formula gives exact expressions for integrating a fifth order polynomial General n-point rules would approximate the integral

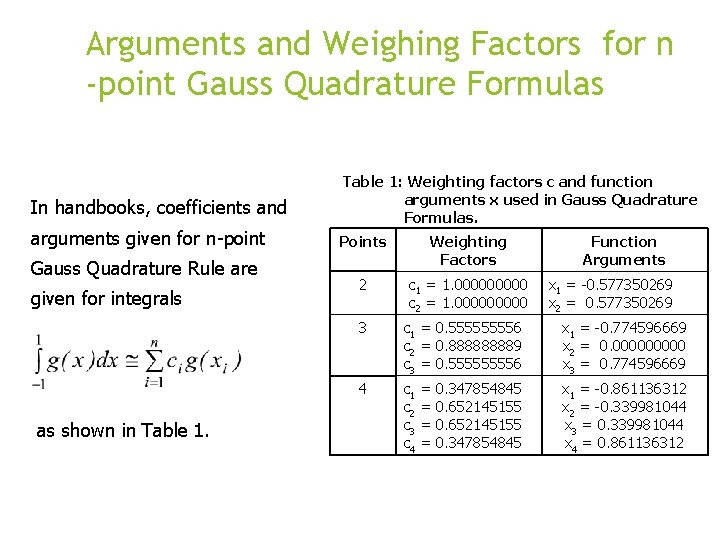
Arguments and Weighing Factors for n -point Gauss Quadrature Formulas In handbooks, coefficients and arguments given for n-point Gauss Quadrature Rule are given for integrals as shown in Table 1: Weighting factors c and function arguments x used in Gauss Quadrature Formulas. Points Weighting Factors 2 c 1 = 1. 00000 c 2 = 1. 00000 Function Arguments x 1 = -0. 577350269 x 2 = 0. 577350269 3 c 1 = 0. 55556 c 2 = 0. 88889 c 3 = 0. 55556 x 1 = -0. 774596669 x 2 = 0. 00000 x 3 = 0. 774596669 4 c 1 c 2 c 3 c 4 x 1 = -0. 861136312 x 2 = -0. 339981044 x 3 = 0. 339981044 x 4 = 0. 861136312 = = 0. 347854845 0. 652145155 0. 347854845

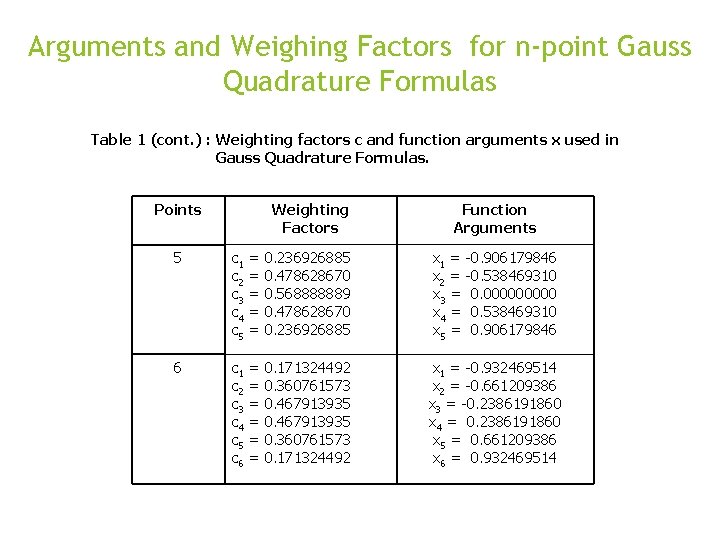
Arguments and Weighing Factors for n-point Gauss Quadrature Formulas Table 1 (cont. ) : Weighting factors c and function arguments x used in Gauss Quadrature Formulas. Points Weighting Factors Function Arguments 5 c 1 c 2 c 3 c 4 c 5 = = = 0. 236926885 0. 478628670 0. 568888889 0. 478628670 0. 236926885 x 1 = -0. 906179846 x 2 = -0. 538469310 x 3 = 0. 00000 x 4 = 0. 538469310 x 5 = 0. 906179846 6 c 1 c 2 c 3 c 4 c 5 c 6 = = = 0. 171324492 0. 360761573 0. 467913935 0. 360761573 0. 171324492 x 1 = -0. 932469514 x 2 = -0. 661209386 x 3 = -0. 2386191860 x 4 = 0. 2386191860 x 5 = 0. 661209386 x 6 = 0. 932469514

Arguments and Weighing Factors for n-point Gauss Quadrature Formulas So if the table is given for ? integrals, how does one solve The answer lies in that any integral with limits of can be converted into an integral with limits If then Let Such that:

Arguments and Weighing Factors for n-point Gauss Quadrature Formulas Then Hence Substituting our values of x, and dx into the integral gives us

Example 1 For an integral derive the one-point Gaussian Quadrature Rule. Solution The one-point Gaussian Quadrature Rule is

Solution The two unknowns x 1, and c 1 are found by assuming that the formula gives exact results for integrating a general first order polynomial, 18

Solution It follows that Equating Equations, the two previous two expressions yield 19

Basis of the Gaussian Quadrature Rule Since the constants a 0, and a 1 are arbitrary giving 20

Solution Hence One-Point Gaussian Quadrature Rule

Example 2 a) Use two-point Gauss Quadrature Rule to approximate the distance covered by a rocket from t=8 to t=30 as given by b) Find the true error, for part (a). c) Also, find the absolute relative true error, for part (a).

Solution First, change the limits of integration from [8, 30] to [-1, 1] by previous relations as follows

Solution (cont) Next, get weighting factors and function argument values from Table 1 for the two point rule,

Solution (cont. ) Now we can use the Gauss Quadrature formula

Solution (cont) since

Solution (cont) b) The true error, , is c) The absolute relative true error, , is (Exact value = 11061. 34 m)