Mecnica Fundamental Conceitos Fundamentais espao tempo sistema de




![Definições Formais e Regras [Ax, Ay, Az] = [Bx, By, Bz] Ax = Bx Definições Formais e Regras [Ax, Ay, Az] = [Bx, By, Bz] Ax = Bx](https://slidetodoc.com/presentation_image/92ceb7187715ae9c0d7f7ad940b37596/image-8.jpg)
![Adição = [soma 1º, soma 2º, soma 3º] Adição = [soma 1º, soma 2º, soma 3º]](https://slidetodoc.com/presentation_image/92ceb7187715ae9c0d7f7ad940b37596/image-9.jpg)





![A Lei Distributiva = c[Ax + Bx, Ay + By, Az + Bz] = A Lei Distributiva = c[Ax + Bx, Ay + By, Az + Bz] =](https://slidetodoc.com/presentation_image/92ceb7187715ae9c0d7f7ad940b37596/image-15.jpg)

![Vetores Unitários = [Ax, Ay, Az] = [Ax, 0, 0] + [0, Ay, 0] Vetores Unitários = [Ax, Ay, Az] = [Ax, 0, 0] + [0, Ay, 0]](https://slidetodoc.com/presentation_image/92ceb7187715ae9c0d7f7ad940b37596/image-17.jpg)




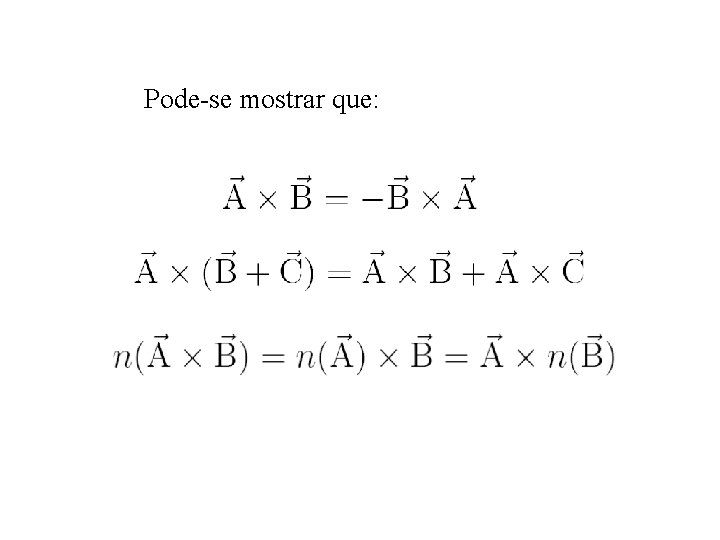
















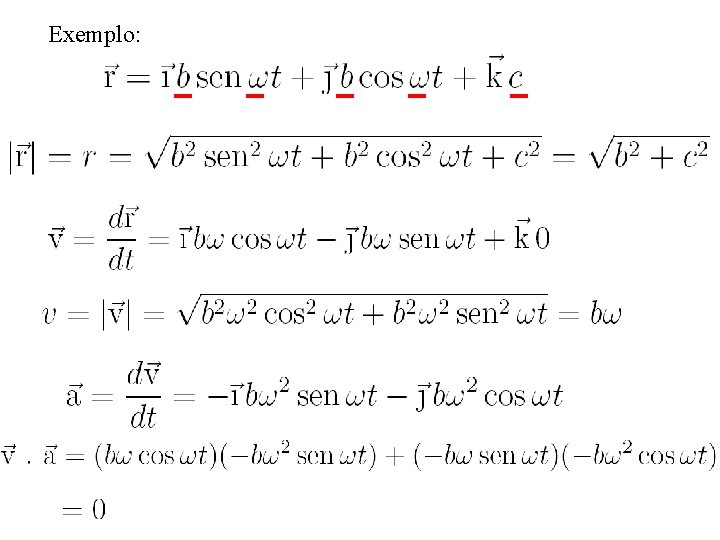


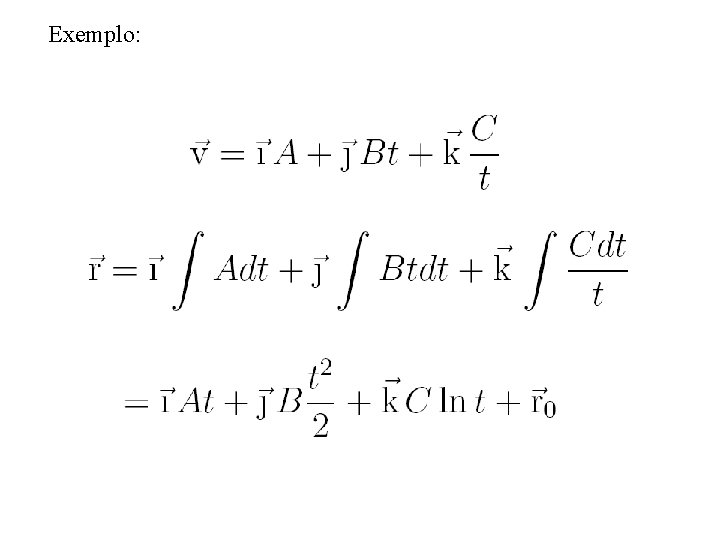





- Slides: 63

Mecânica Fundamental

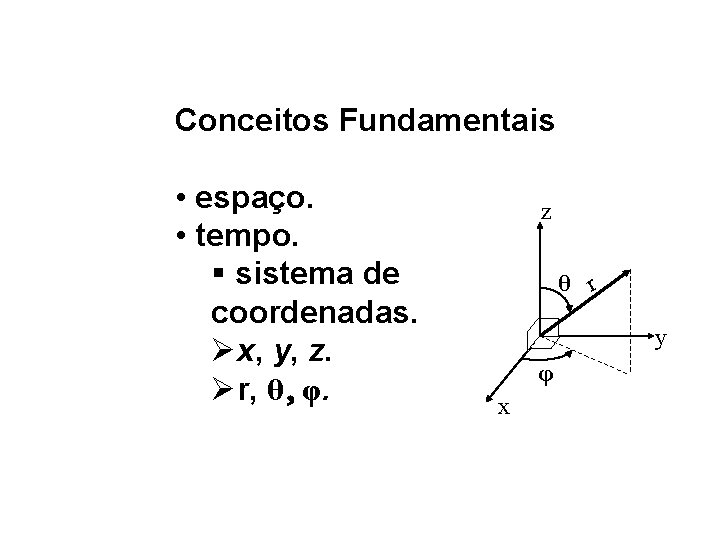
Conceitos Fundamentais • espaço. • tempo. § sistema de coordenadas. Øx, y, z. Ør, θ, φ. z θ r y φ x

Partícula ou ponto de massa • tem massa mas não extensão espacial.

Grandezas Físicas e Unidades A unidade padrão de comprimento é o metro. m A unidade padrão de massa é o quilograma. kg 0. 00 1. 00 A unidade padrão de tempo é o segundo. s

Grandezas Escalares e Vetoriais • Escalar. (densidade, volume e temperatura. ) • Vetores. (deslocamento espacial)

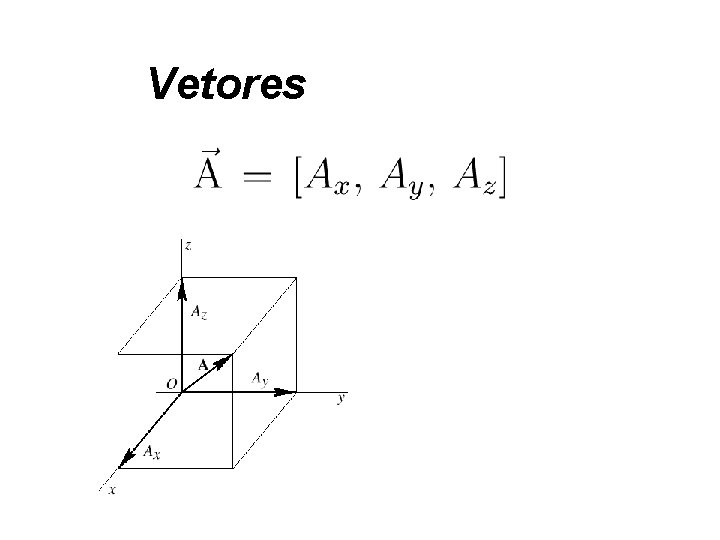
Vetores

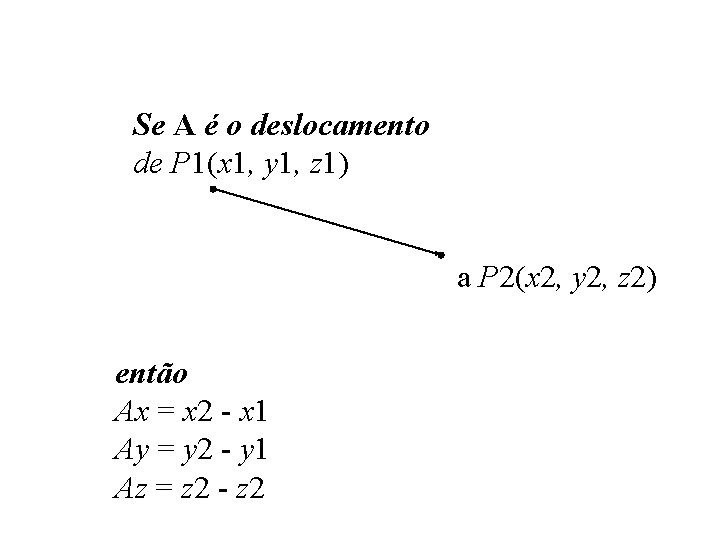
Se A é o deslocamento de P 1(x 1, y 1, z 1) a P 2(x 2, y 2, z 2) então Ax = x 2 - x 1 Ay = y 2 - y 1 Az = z 2 - z 2
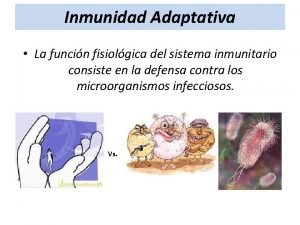
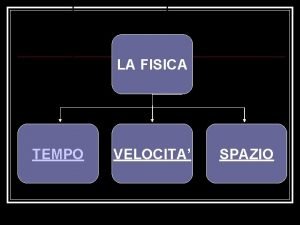
![Definições Formais e Regras Ax Ay Az Bx By Bz Ax Bx Definições Formais e Regras [Ax, Ay, Az] = [Bx, By, Bz] Ax = Bx](https://slidetodoc.com/presentation_image/92ceb7187715ae9c0d7f7ad940b37596/image-8.jpg)
Definições Formais e Regras [Ax, Ay, Az] = [Bx, By, Bz] Ax = Bx Ay = By Az = Bz
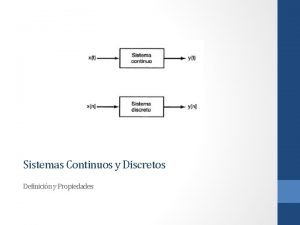
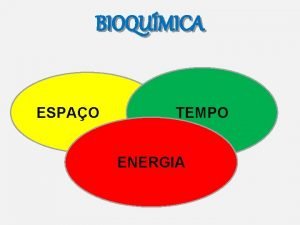
![Adição soma 1º soma 2º soma 3º Adição = [soma 1º, soma 2º, soma 3º]](https://slidetodoc.com/presentation_image/92ceb7187715ae9c0d7f7ad940b37596/image-9.jpg)
Adição = [soma 1º, soma 2º, soma 3º]

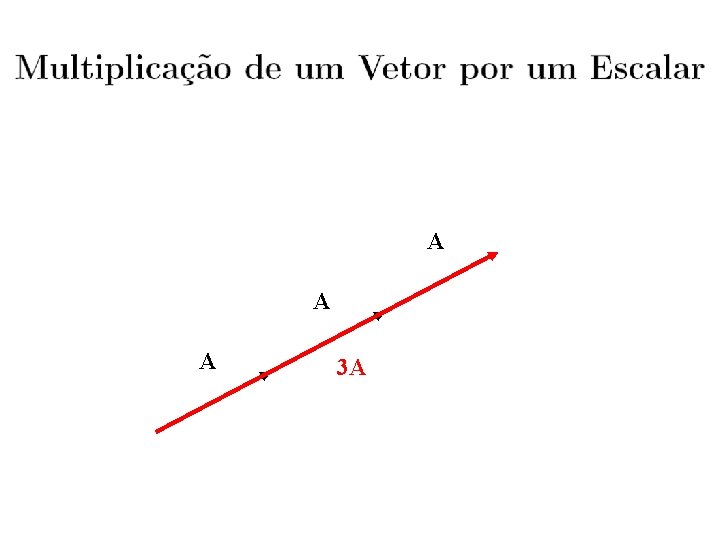
Multiplicação por um Escalar

Subtração de Vetores

O Vetor Nulo

A Lei Comutativa da Adição Exemplo:

A Lei Associativa = [Ax + (Bx + Cx), Ay + (By + Cy), Az + (Bz + Cz)] = [(Ax + Bx) + Cx, (Ay + By) + Cy, (Az + Bz) + Cz ]
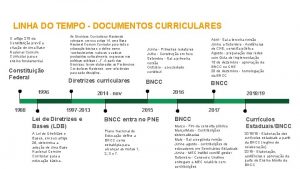
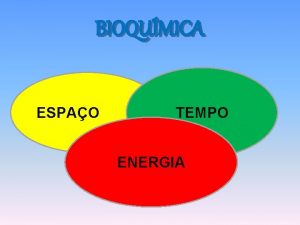
![A Lei Distributiva cAx Bx Ay By Az Bz A Lei Distributiva = c[Ax + Bx, Ay + By, Az + Bz] =](https://slidetodoc.com/presentation_image/92ceb7187715ae9c0d7f7ad940b37596/image-15.jpg)
A Lei Distributiva = c[Ax + Bx, Ay + By, Az + Bz] = [c(Ax + Bx), c(Ay + By), c(Az + Bz)] = [c. Ax + c. Bx, c. Ay + c. By, c. Az + c. Bz]

Módulo de um Vetor
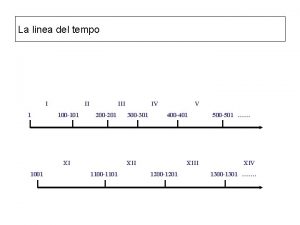
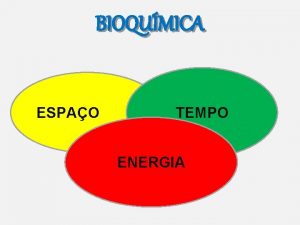
![Vetores Unitários Ax Ay Az Ax 0 0 0 Ay 0 Vetores Unitários = [Ax, Ay, Az] = [Ax, 0, 0] + [0, Ay, 0]](https://slidetodoc.com/presentation_image/92ceb7187715ae9c0d7f7ad940b37596/image-17.jpg)
Vetores Unitários = [Ax, Ay, Az] = [Ax, 0, 0] + [0, Ay, 0] + [0, 0, Az] = Ax [1, 0, 0] + Ay [0, 1, 0] + Az [0, 0, 1]

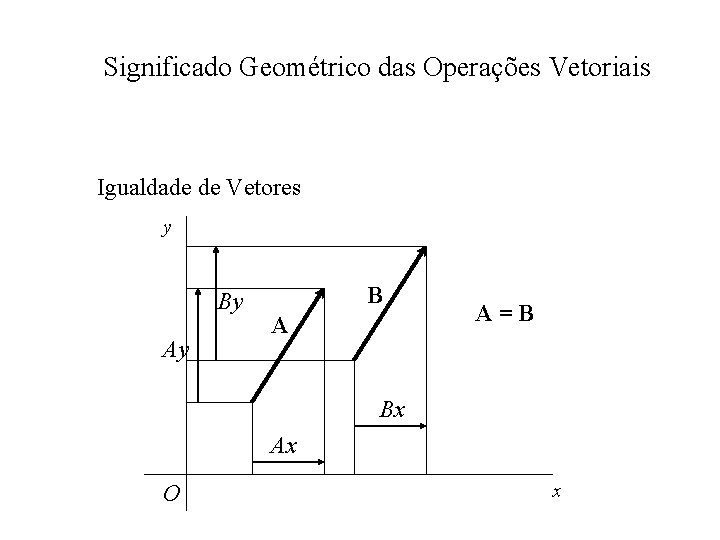
Significado Geométrico das Operações Vetoriais Igualdade de Vetores y By Ay B A A=B Bx Ax O x

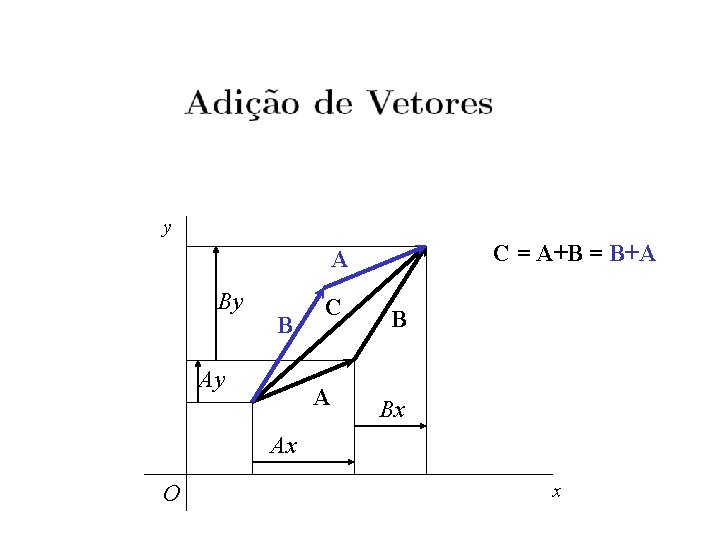
y C = A+B = B+A A By B Ay C A B Bx Ax O x

O negativo de um vetor. A -A

A A A 3 A

O Produto Escalar Assim: = Ax(Bx + Cx) + Ay(By + Cy) + Az (Bz + Cz) = A x B x + A y B y + A z. B z + A x C x + A y C y + A z. C z

Definição alternativa do produto escalar.

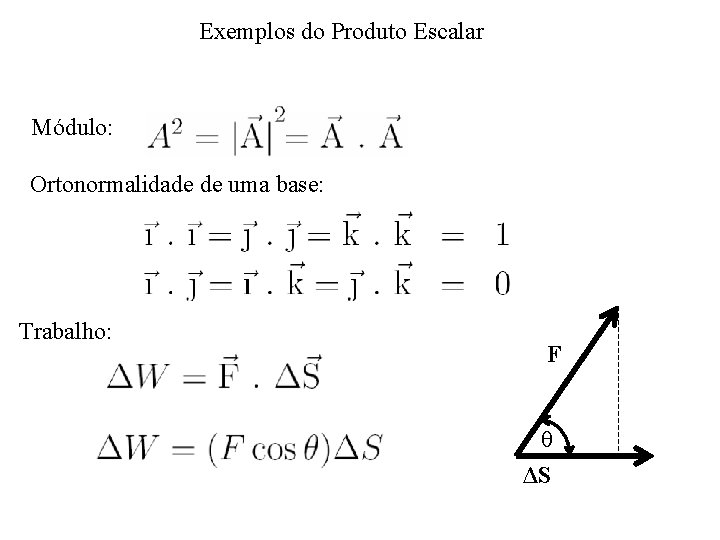
Exemplos do Produto Escalar Módulo: Ortonormalidade de uma base: Trabalho: F θ ΔS

Lei dos Cossenos

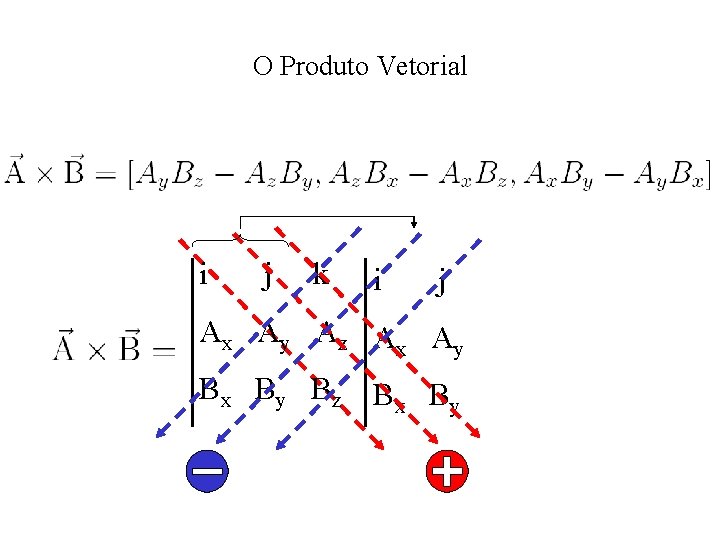
O Produto Vetorial i j k i j Ax Ay Az Ax Ay Bx By Bz Bx By
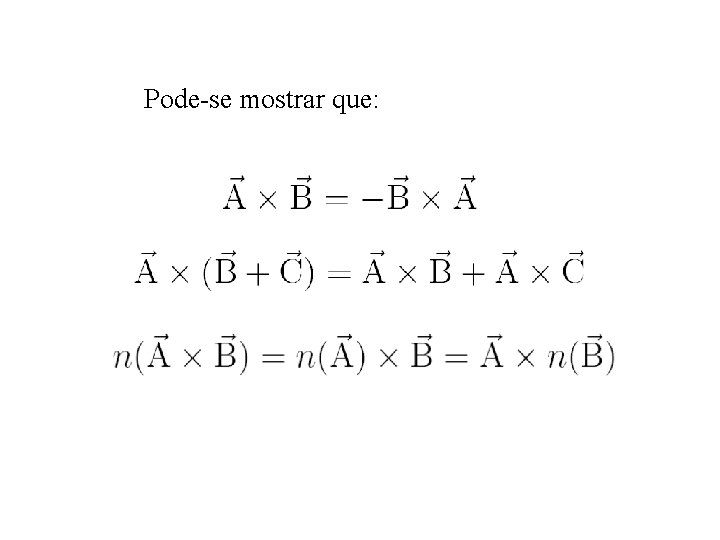
Pode-se mostrar que:

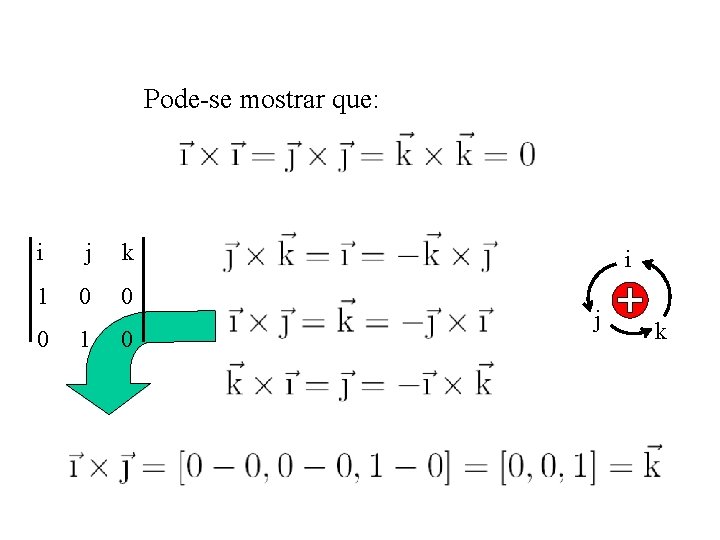
Pode-se mostrar que: i j k 1 0 0 0 1 0 i j k

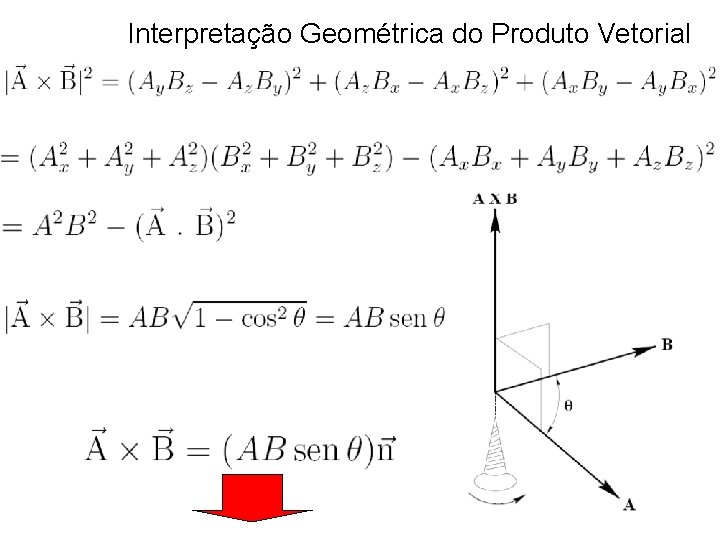
Interpretação Geométrica do Produto Vetorial

Ortogonalidade do produto vetorial = A x C x + A y C y + A z. C z = Ax (Ay. Bz - Az. By) + Ay (Az. Bx - Ax. Bz) + Az (Ax. By - Ay. Bx) = A x A y B z - A z. B y A x + A y A z. B x - A x B z A y + A z. A x B y - A y B x A z =0


ngulo entre A e B

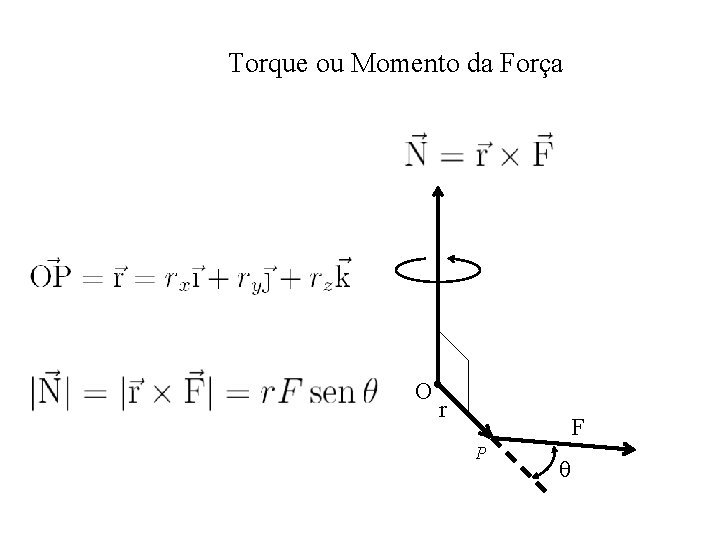
Torque ou Momento da Força O r F P θ

Cossenos diretores Ex: seja n unitario de A

Ex: encontrar o unitário perpendicular aos vetores

Produtos Triplos Comutando duas linhas Prove que:

Aula 2 Derivada de vetores Integral de vetores Transformações de sistemas de coordenadas Velocidade relativa Aceleração normal e tangencial







Derivada de um Vetor

Vetor Posição de uma Partícula y r O z ix jy x kz

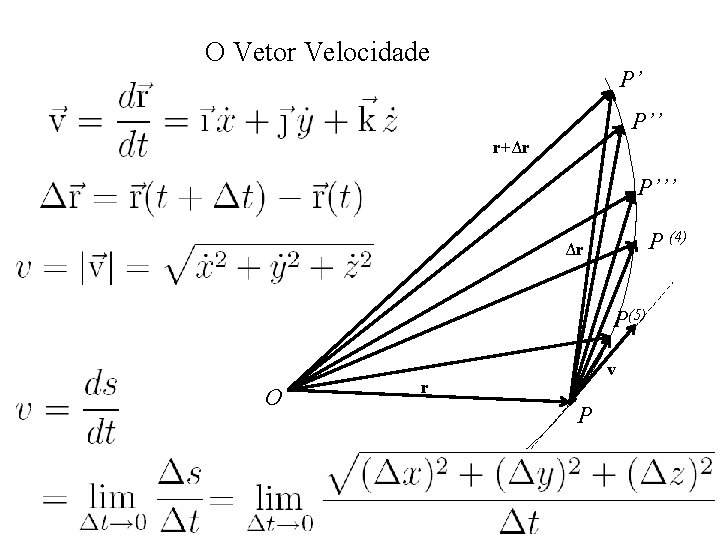
O Vetor Velocidade P’ P’’ r+Δr P’’’ P (4) Δr P(5) O v r P

Vetor Aceleração

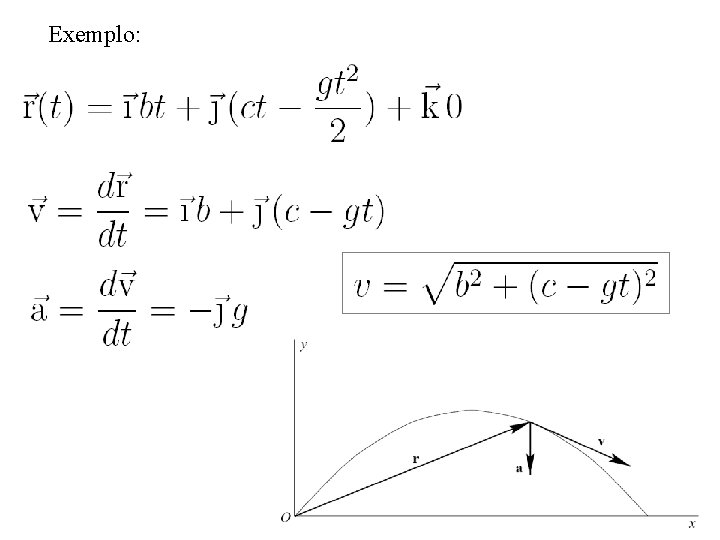
Exemplo:
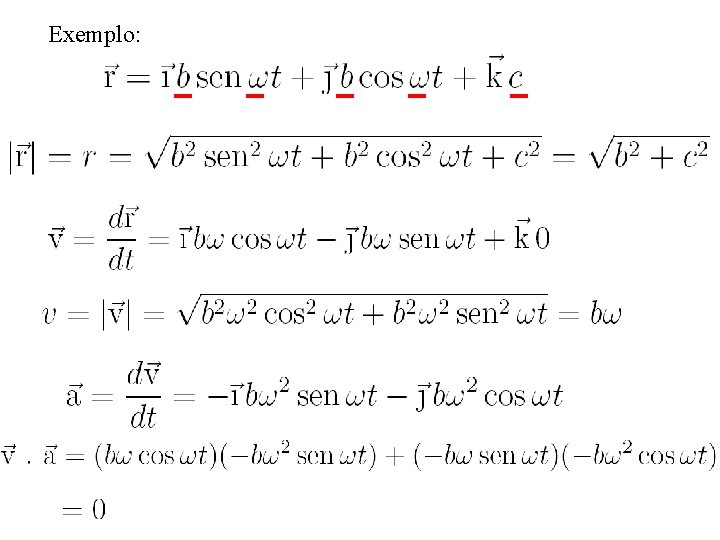
Exemplo:


Integração Vetorial
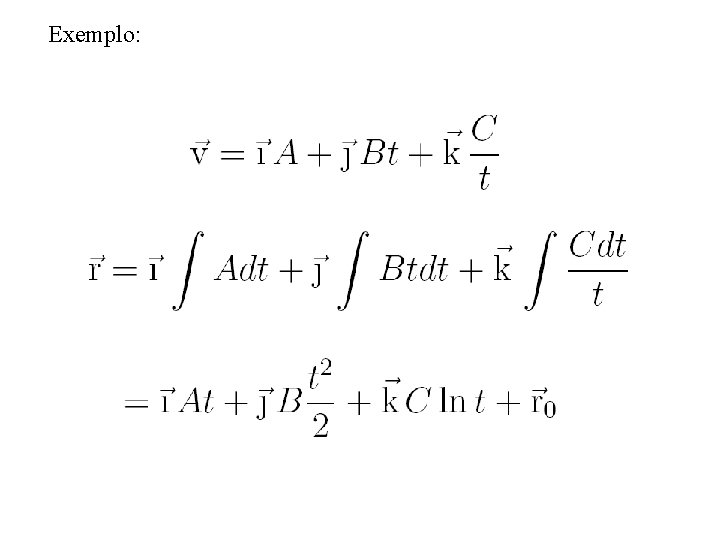
Exemplo:

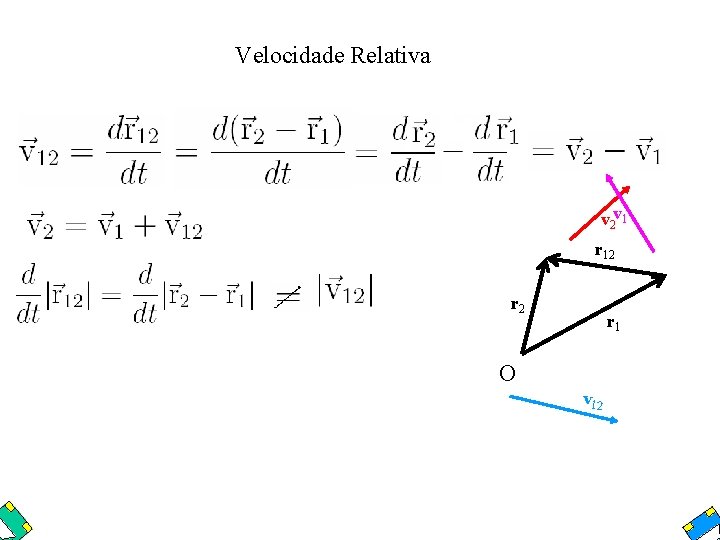
Velocidade Relativa v 2 v 1 r 12 r 1 O v 12

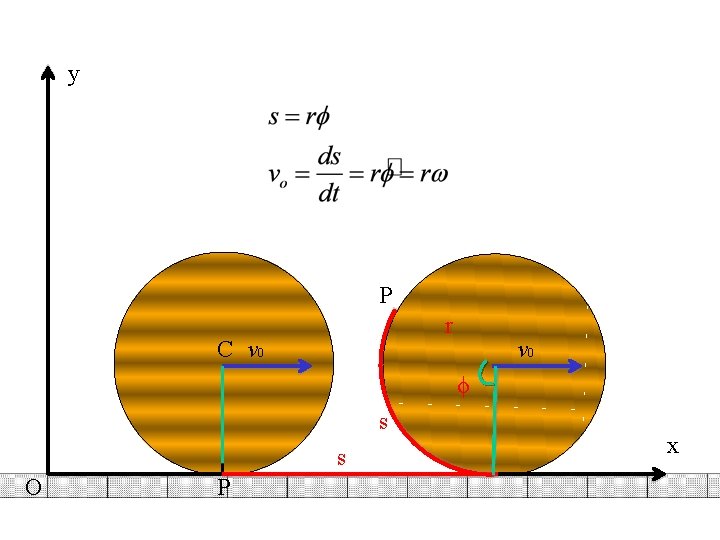
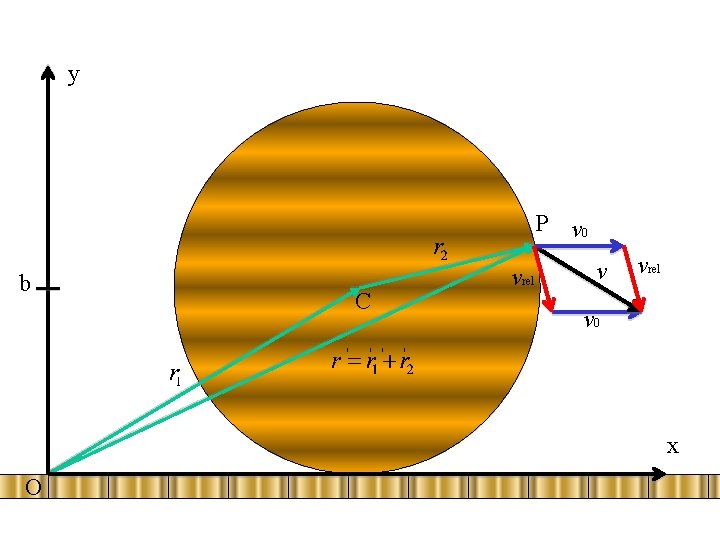
y P r C v 0 ϕ s s O P x

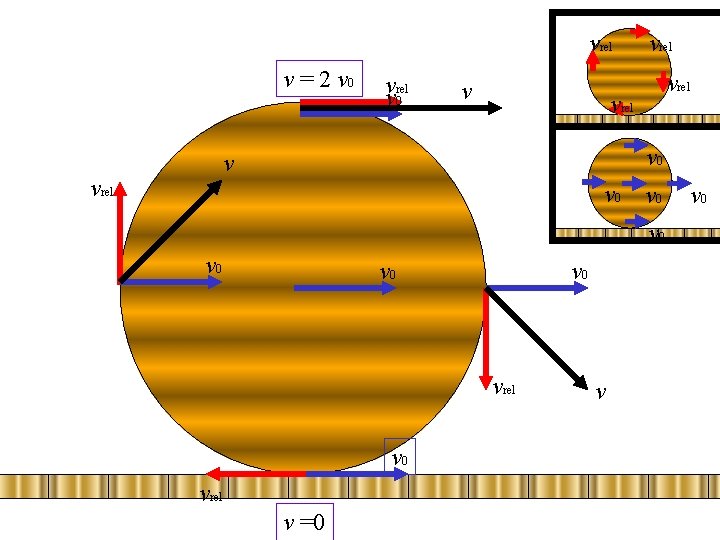
vrel v = 2 v 0 vvrel 0 v vrel v 0 v 0 v 0 vrel v =0 v v 0

y P v 0 b C vrel v 0 x O

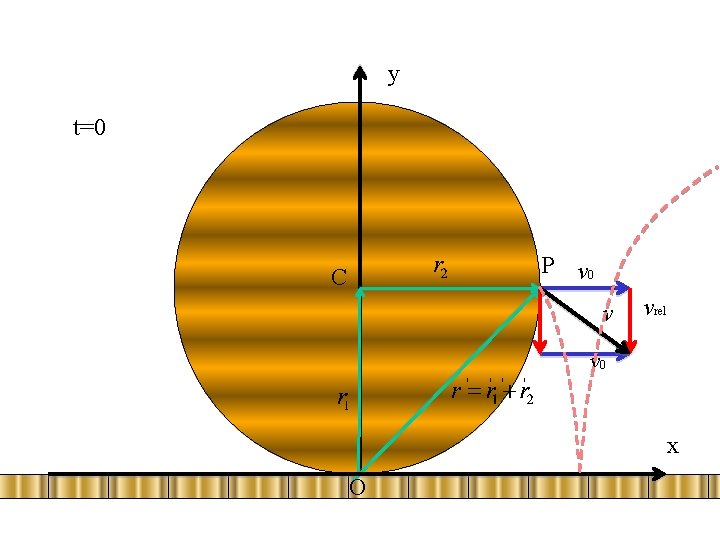
y t=0 P v 0 C v vrel v 0 x O


Derivadas de Produtos de Vetores



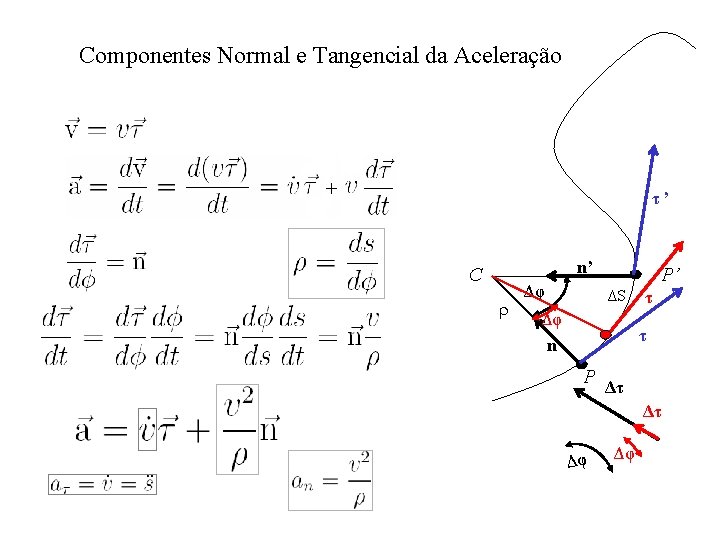
Componentes Normal e Tangencial da Aceleração τ’ n’ C r Δφ P’ ΔS Δφ n τ τ P Δτ Δτ Δφ Δφ

Esta apresentação foi desenvolvida pelo Prof. Gustavo de Almeida Magalhães Sáfar e corrigida, conferida e ampliada pelo Prof. João Francisco C. Santos Jr. no Departamento de Física do Instituto de Ciências Exatas da Universidade Federal de Minas Gerais.
 De marketing
De marketing Conceitos de calor e temperatura
Conceitos de calor e temperatura Espao
Espao Hydrostatic force on surface
Hydrostatic force on surface Mecnica
Mecnica Erro relativo
Erro relativo Formas fundamentais de energia.
Formas fundamentais de energia. Teoria dos direitos fundamentais robert alexy
Teoria dos direitos fundamentais robert alexy Grandezas fundamentais e derivadas
Grandezas fundamentais e derivadas Estudo das leis gerais do pensamento
Estudo das leis gerais do pensamento Cavitação
Cavitação Limite bilateral
Limite bilateral Direitos fundamentais
Direitos fundamentais Arrume tempo para ser feliz
Arrume tempo para ser feliz Perdemos muito tempo
Perdemos muito tempo Conceitos gerais da ecologia
Conceitos gerais da ecologia Ecologia
Ecologia O que e ecologia
O que e ecologia Conceitos básicos em ecologia
Conceitos básicos em ecologia Classificação de software
Classificação de software Conceitos básicos de clp
Conceitos básicos de clp Símbolo do florescimento cultural científico
Símbolo do florescimento cultural científico Conceitos de hidrografia
Conceitos de hidrografia Reposta
Reposta Estrutura do sfn
Estrutura do sfn Conceitos de solid
Conceitos de solid Arquitetura cliente servidor
Arquitetura cliente servidor Sistema operacional
Sistema operacional Organos linfaticos secundarios
Organos linfaticos secundarios Vistas sistema europeo
Vistas sistema europeo Unilever kodaikanal
Unilever kodaikanal Que son los sistemas continuos
Que son los sistemas continuos Sistema semashko o sistema centralizado
Sistema semashko o sistema centralizado Cuaresma tiempo de cambiar
Cuaresma tiempo de cambiar Meridiano local
Meridiano local Tempo italian terms
Tempo italian terms Eis o tempo de conversão eis o dia da salvação
Eis o tempo de conversão eis o dia da salvação Agogika v hudbe
Agogika v hudbe Tabella tempo/temperatura sterilizzazione
Tabella tempo/temperatura sterilizzazione O tempo passou e me formei em solidão
O tempo passou e me formei em solidão Lei das doze tábuas
Lei das doze tábuas Genetograma
Genetograma Caracteristicas realismo
Caracteristicas realismo Queda livre dos corpos
Queda livre dos corpos Percussion bar of the ifugao.
Percussion bar of the ifugao. šta je takt
šta je takt Tempo van oplossing
Tempo van oplossing Esportivização da capoeira
Esportivização da capoeira O valioso tempo dos maduros mário de andrade
O valioso tempo dos maduros mário de andrade Mario de andrade o valioso tempo dos maduros
Mario de andrade o valioso tempo dos maduros Analepse
Analepse O tempo é inexorável
O tempo é inexorável Poema da jabuticaba
Poema da jabuticaba 7
7 Velocidade de um carro
Velocidade de um carro Modalidades organizativas do tempo didático
Modalidades organizativas do tempo didático Marine traffic mapa de navios em tempo real
Marine traffic mapa de navios em tempo real Atividade sobre tempos verbais 6 ano
Atividade sobre tempos verbais 6 ano Vidro tempo de decomposição
Vidro tempo de decomposição Bncc linha do tempo
Bncc linha do tempo Reazione di presa
Reazione di presa Linea del tempo odissea
Linea del tempo odissea Velocità spazio tempo
Velocità spazio tempo Tempo misto coscienza di zeno
Tempo misto coscienza di zeno