Manejo de Espacios y Cantidades CONALEP TIZAYUCA DOCENTE

Manejo de Espacios y Cantidades

CONALEP TIZAYUCA � DOCENTE: � ING. MIRNA PINEDA PÉREZ � Febrero- Junio 2011

UNIDAD 1 “Manejo de campos numéricos y relaciones entre cantidades”

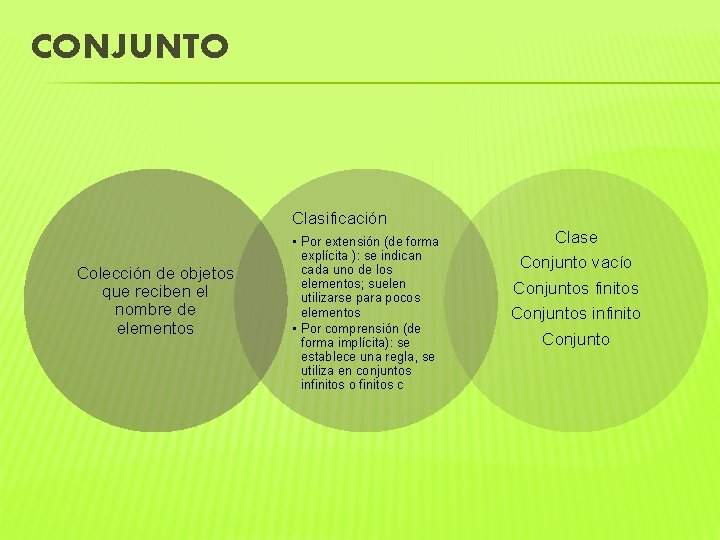
CONJUNTO Clasificación Colección de objetos que reciben el nombre de elementos • Por extensión (de forma explícita ): se indican cada uno de los elementos; suelen utilizarse para pocos elementos • Por comprensión (de forma implícita): se establece una regla, se utiliza en conjuntos infinitos o finitos c Clase Conjunto vacío Conjuntos finitos Conjuntos infinito Conjunto

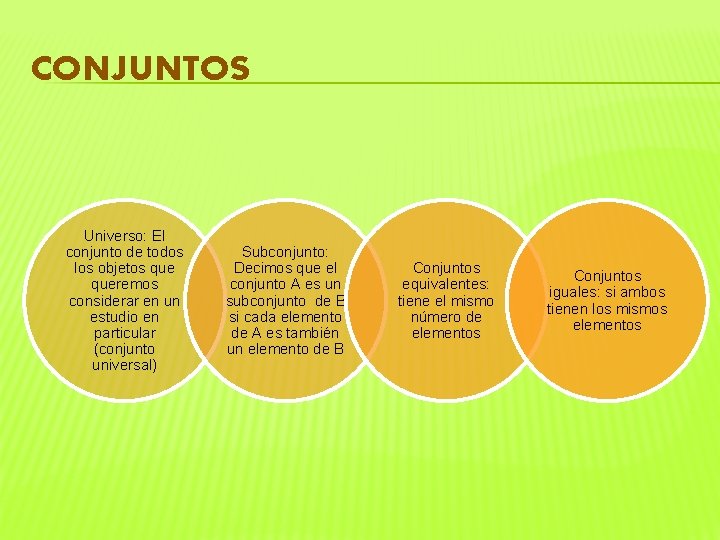
CONJUNTOS Universo: El conjunto de todos los objetos queremos considerar en un estudio en particular (conjunto universal) Subconjunto: Decimos que el conjunto A es un subconjunto de B si cada elemento de A es también un elemento de B Conjuntos equivalentes: tiene el mismo número de elementos Conjuntos iguales: si ambos tienen los mismos elementos

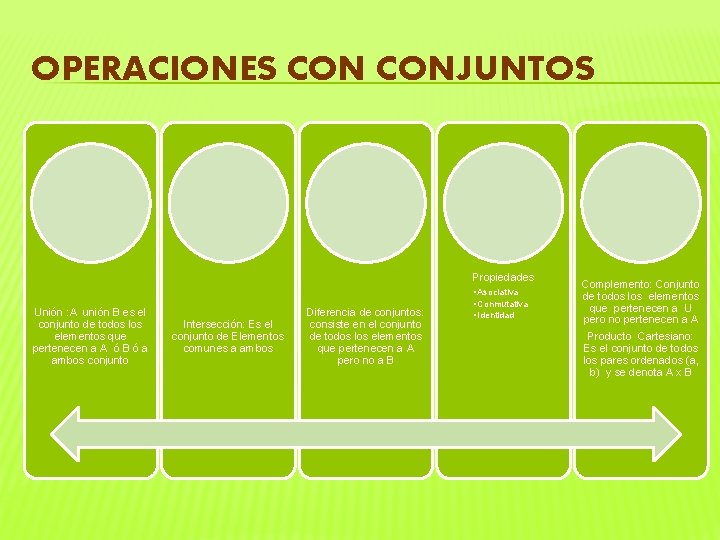
OPERACIONES CONJUNTOS Propiedades Unión : A unión B es el conjunto de todos los elementos que pertenecen a A ó B ó a ambos conjunto Intersección: Es el conjunto de Elementos comunes a ambos Diferencia de conjuntos: consiste en el conjunto de todos los elementos que pertenecen a A pero no a B • Asociativa • Conmutativa • Identidad Complemento: Conjunto de todos los elementos que pertenecen a U pero no pertenecen a A Producto Cartesiano: Es el conjunto de todos los pares ordenados (a, b) y se denota A x B

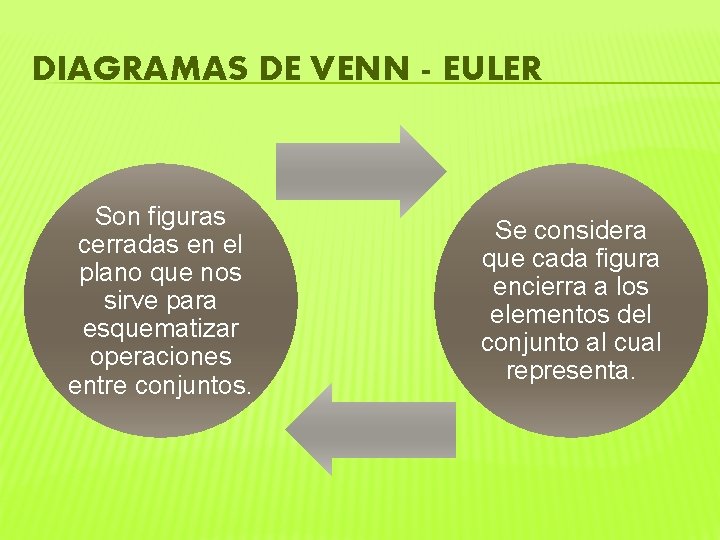
DIAGRAMAS DE VENN - EULER Son figuras cerradas en el plano que nos sirve para esquematizar operaciones entre conjuntos. Se considera que cada figura encierra a los elementos del conjunto al cual representa.

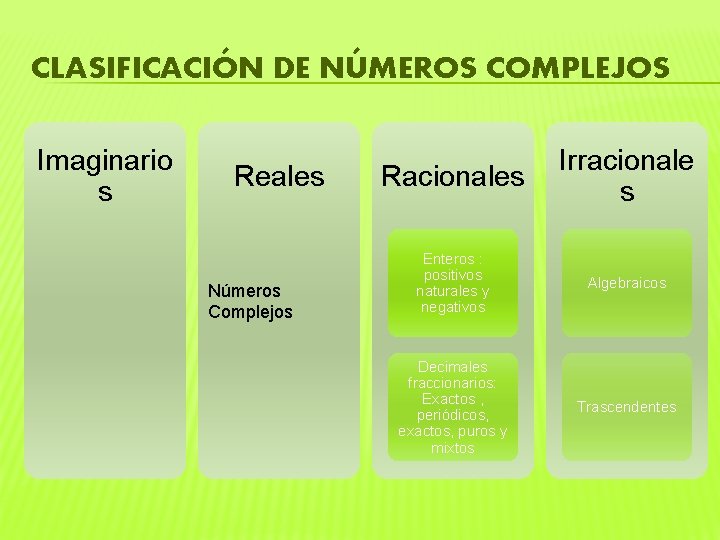
CLASIFICACIÓN DE NÚMEROS COMPLEJOS Imaginario s Reales Números Complejos Racionales Irracionale s Enteros : positivos naturales y negativos Algebraicos Decimales fraccionarios: Exactos , periódicos, exactos, puros y mixtos Trascendentes

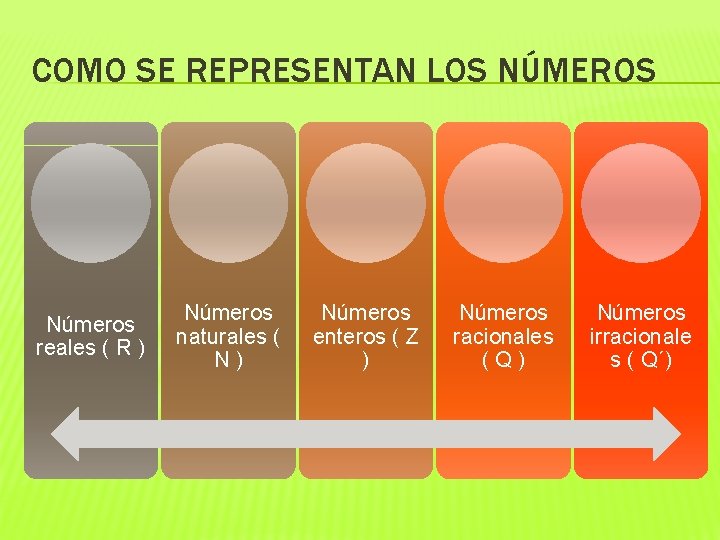
COMO SE REPRESENTAN LOS NÚMEROS Números reales ( R ) Números naturales ( N) Números enteros ( Z ) Números racionales (Q) Números irracionale s ( Q´)

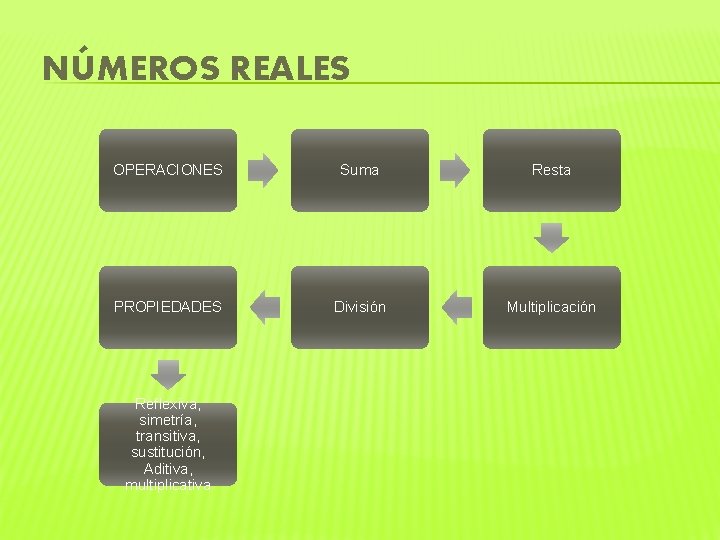
NÚMEROS REALES OPERACIONES Suma Resta PROPIEDADES División Multiplicación Reflexiva, simetría, transitiva, sustitución, Aditiva, multiplicativa

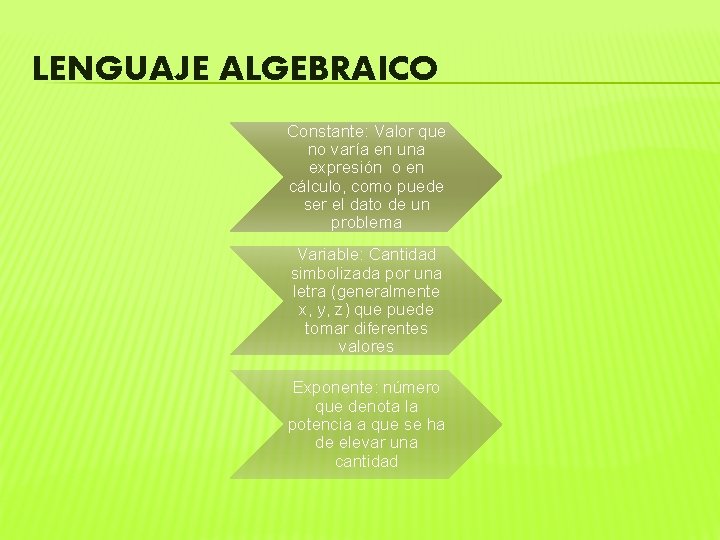
LENGUAJE ALGEBRAICO Constante: Valor que no varía en una expresión o en cálculo, como puede ser el dato de un problema Variable: Cantidad simbolizada por una letra (generalmente x, y, z) que puede tomar diferentes valores Exponente: número que denota la potencia a que se ha de elevar una cantidad

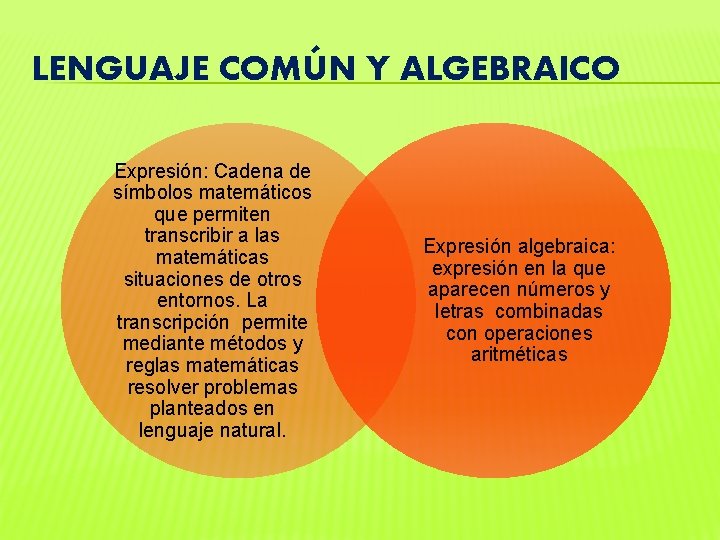
LENGUAJE COMÚN Y ALGEBRAICO Expresión: Cadena de símbolos matemáticos que permiten transcribir a las matemáticas situaciones de otros entornos. La transcripción permite mediante métodos y reglas matemáticas resolver problemas planteados en lenguaje natural. Expresión algebraica: expresión en la que aparecen números y letras combinadas con operaciones aritméticas

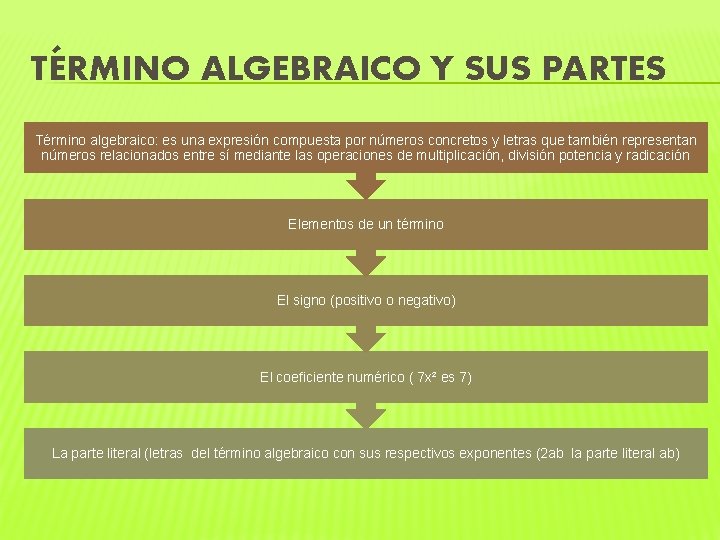
TÉRMINO ALGEBRAICO Y SUS PARTES Término algebraico: es una expresión compuesta por números concretos y letras que también representan números relacionados entre sí mediante las operaciones de multiplicación, división potencia y radicación Elementos de un término El signo (positivo o negativo) El coeficiente numérico ( 7 x² es 7) La parte literal (letras del término algebraico con sus respectivos exponentes (2 ab la parte literal ab)

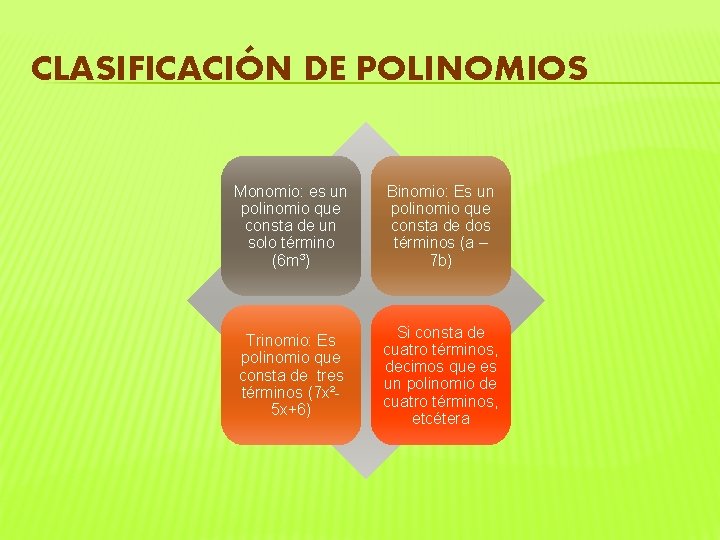
CLASIFICACIÓN DE POLINOMIOS Monomio: es un polinomio que consta de un solo término (6 m³) Binomio: Es un polinomio que consta de dos términos (a – 7 b) Trinomio: Es polinomio que consta de tres términos (7 x² 5 x+6) Si consta de cuatro términos, decimos que es un polinomio de cuatro términos, etcétera

UNIDAD 2 “Manejo de operaciones con expresiones algebraicas”

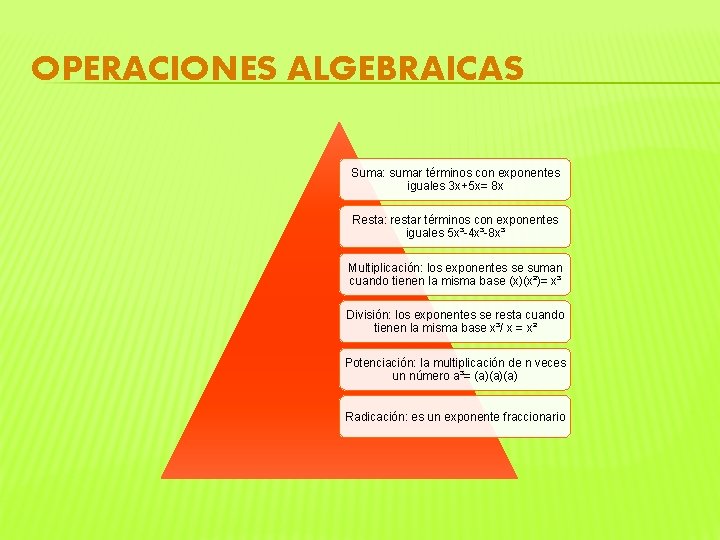
OPERACIONES ALGEBRAICAS Suma: sumar términos con exponentes iguales 3 x+5 x= 8 x Resta: restar términos con exponentes iguales 5 x³-4 x³-8 x³ Multiplicación: los exponentes se suman cuando tienen la misma base (x)(x²)= x³ División: los exponentes se resta cuando tienen la misma base x³/ x = x² Potenciación: la multiplicación de n veces un número a³= (a)(a)(a) Radicación: es un exponente fraccionario

TÉRMINOS SEMEJANTES Conjunto de términos que tienen la misma parte literal, es decir, que al eliminar los números que forman los coeficientes, son idénticos 3 x²y es un término semejante a -¼x²y pero no a 5 xy³

REDUCIR TÉRMINOS SEMEJANTES Frecuentemente en la resolución de problemas algebraicos se requiere reducir términos semejantes por uno sólo, que resulta de la suma algebraica de sus coeficientes numéricos multiplicados por su parte literal Casos Reducir términos semejantes que tienen el mismo signo Reducir términos que tienen diferente signo Reducir tres o más términos semejantes que no tienen todos el mismo signo

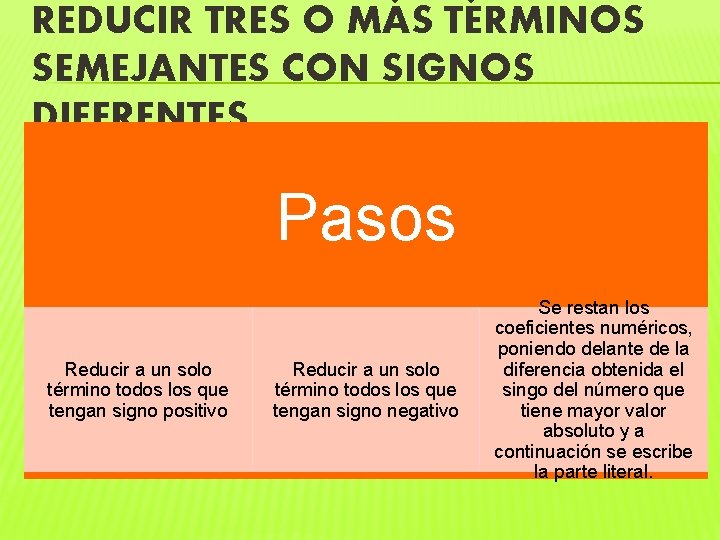
REDUCIR TRES O MÁS TÉRMINOS SEMEJANTES CON SIGNOS DIFERENTES Pasos Reducir a un solo término todos los que tengan signo positivo Reducir a un solo término todos los que tengan signo negativo Se restan los coeficientes numéricos, poniendo delante de la diferencia obtenida el singo del número que tiene mayor valor absoluto y a continuación se escribe la parte literal.

ADICIÓN DE POLINOMIOS Suma Es importante que los polinomios que se suman se ordenen todos con respecto a una misma letra ya sea en forma descendente o ascendente, es decir que los exponentes de una letra escogida vaya aumentando o disminuyendo de uno en uno Reducir los términos semejantes Escribir los polinomios en renglones sucesivos de tal forma que los términos semejantes queden en la misma columna y a continuación reducir

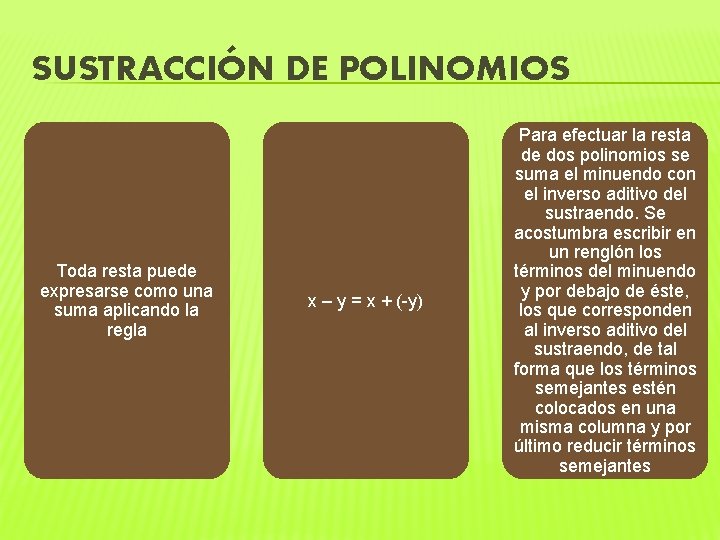
SUSTRACCIÓN DE POLINOMIOS Toda resta puede expresarse como una suma aplicando la regla x – y = x + (-y) Para efectuar la resta de dos polinomios se suma el minuendo con el inverso aditivo del sustraendo. Se acostumbra escribir en un renglón los términos del minuendo y por debajo de éste, los que corresponden al inverso aditivo del sustraendo, de tal forma que los términos semejantes estén colocados en una misma columna y por último reducir términos semejantes

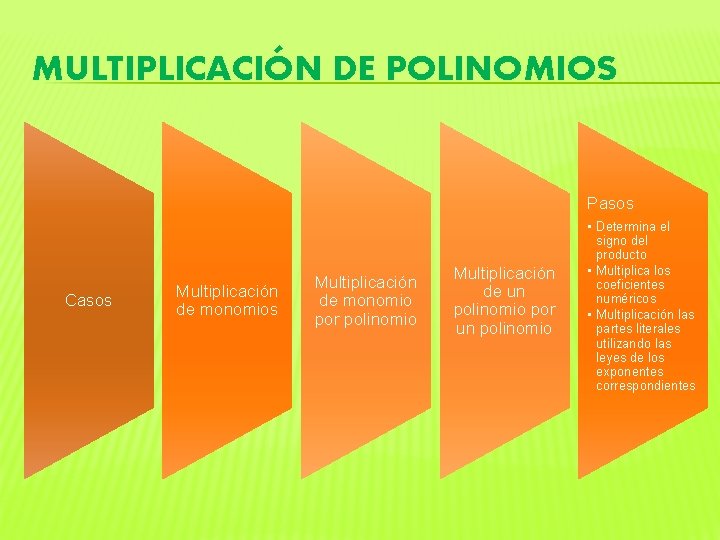
MULTIPLICACIÓN DE POLINOMIOS Pasos Casos Multiplicación de monomio por polinomio Multiplicación de un polinomio por un polinomio • Determina el signo del producto • Multiplica los coeficientes numéricos • Multiplicación las partes literales utilizando las leyes de los exponentes correspondientes

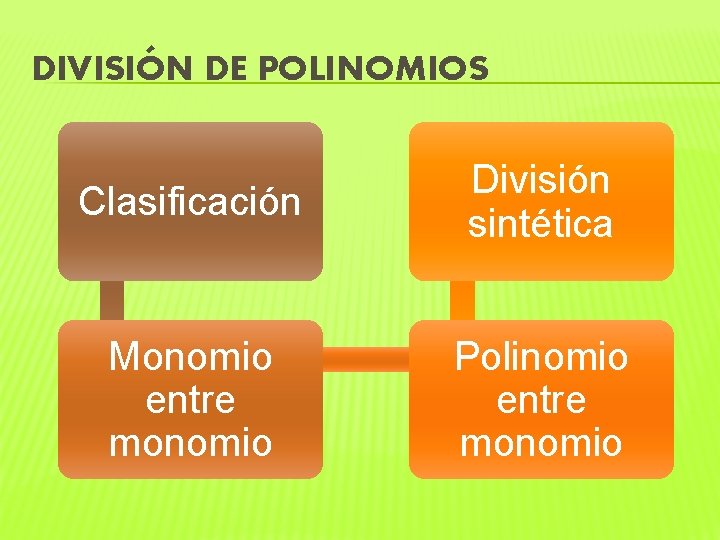
DIVISIÓN DE POLINOMIOS Clasificación División sintética Monomio entre monomio Polinomio entre monomio

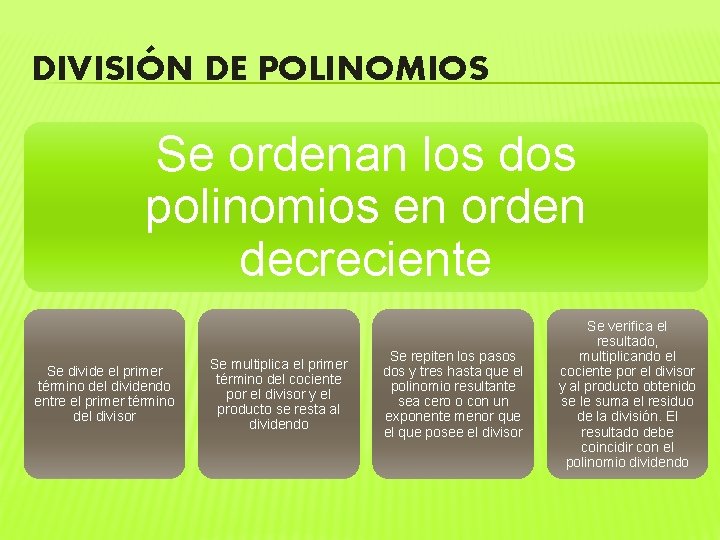
DIVISIÓN DE POLINOMIOS Se ordenan los dos polinomios en orden decreciente Se divide el primer término del dividendo entre el primer término del divisor Se multiplica el primer término del cociente por el divisor y el producto se resta al dividendo Se repiten los pasos dos y tres hasta que el polinomio resultante sea cero o con un exponente menor que el que posee el divisor Se verifica el resultado, multiplicando el cociente por el divisor y al producto obtenido se le suma el residuo de la división. El resultado debe coincidir con el polinomio dividendo

EXPONENTES Propiedades Regla del producto de potencia de igual base Regla de la base con exponente cero Regla de exponente negativo Regla de potencia de una potencia

RADICALES Operaciones con radicales Suma y resta de radicales: semejantes Multiplicación de radicales Con el mismo índice Con diferente índice Conjugados Multiplicación de conjugados

PRODUCTOS NOTABLES Al multiplicar algunos tipos de expresiones algebraicas se obtienen productos en que se distinguen algunos rasgos notables, de los cuales permiten efectuar dichas operaciones en forma rápida al aplicar la regla correspondiente Binomio al cuadrado Binomios con término en común Binomios conjugados Binomio al cubo

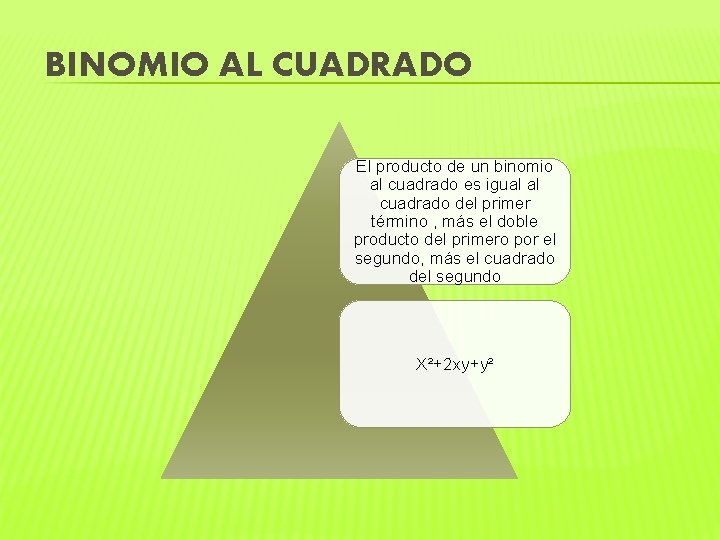
BINOMIO AL CUADRADO El producto de un binomio al cuadrado es igual al cuadrado del primer término , más el doble producto del primero por el segundo, más el cuadrado del segundo X²+2 xy+y²

BINOMIOS CONJUGADOS El producto de un binomio por su conjugado es igual al cuadrado del segundo”, donde consideremos como primer término aquel que tiene signo positivo en ambos binomios (x + y)(x – y) = x² - y²

BINOMIOS CON TÉRMINO EN COMÚN El producto de dos términos en común es igual al cuadrado del término en común, más el producto del término común por la suma de los no comunes, más el producto de los términos no comunes (x + a)(x + b)= x²+ x(b + a) +ab

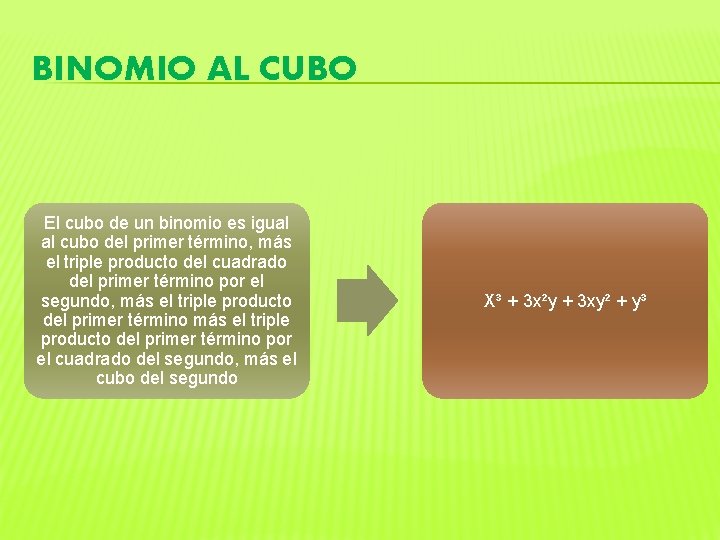
BINOMIO AL CUBO El cubo de un binomio es igual al cubo del primer término, más el triple producto del cuadrado del primer término por el segundo, más el triple producto del primer término por el cuadrado del segundo, más el cubo del segundo X³ + 3 x²y + 3 xy² + y³

FACTORIZACIÓN Descomposición en factores o números primos Factorizar una expresión algebraica es reescribirla como el producto de sus factores X²-y²= (x + y)(x - y)

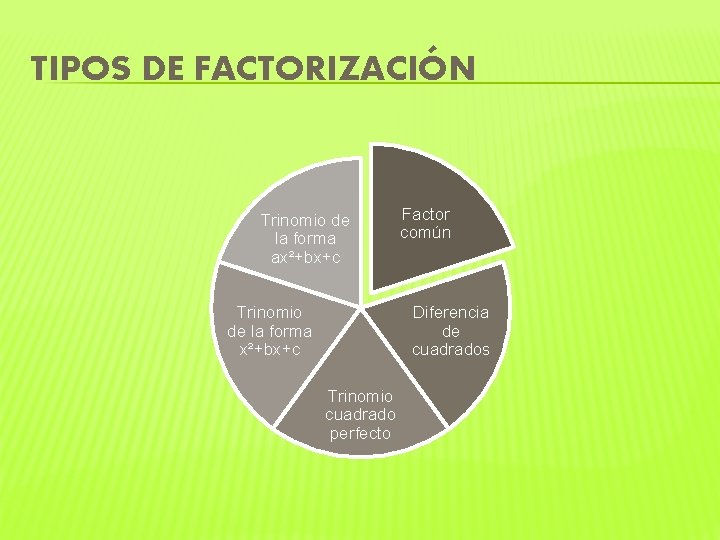
TIPOS DE FACTORIZACIÓN Trinomio de la forma ax²+bx+c Trinomio de la forma x²+bx+c Factor común Diferencia de cuadrados Trinomio cuadrado perfecto

FACTOR COMÚN Cuando cada uno de los términos de un polinomio tienen un factor común, la ley distributiva de la multiplicación nos permite expresarlo como el producto de dos factores, donde uno de ellos es el monomio factor común • 8 b²-32 b³= 8 b²(1 – 4 b)

FACTOR COMÚN Pasos Determinar el máximo común factor común de los coeficientes numéricos de los términos del polinomio, es el número que resulta del producto de los factores primos comunes a todos ellos afectados por sus potencias mínimas Encuentra el máximo factor común de las partes literales de cada uno de sus términos del polinomio, el cual será el producto de los factores literales comunes a todas ellas afectadas por su mínima potencia Encuentra el máximo factor común del polinomio, el cual resulta de multiplicar el máximo común divisor de los coeficientes numéricos del polinomio por el máximo factor común de las partes literales de sus términos Expresa cada uno de los términos del polinomio como el producto del máximo factor por el monomio que resulta al dividir cada término entre dicho máximo factor común Factoriza la expresión que resulta del paso anterior

DIFERENCIA DE CUADRADOS Pasos • Extraer la raíz cuadrada a cada uno de sus términos • Construye un binomio con las raíces obtenidas escribiendo el signo (-) entre ellas • Multiplica el binomio que resulta del paso anterior por su conjugado • a² - b²= (a + b)(a – b)

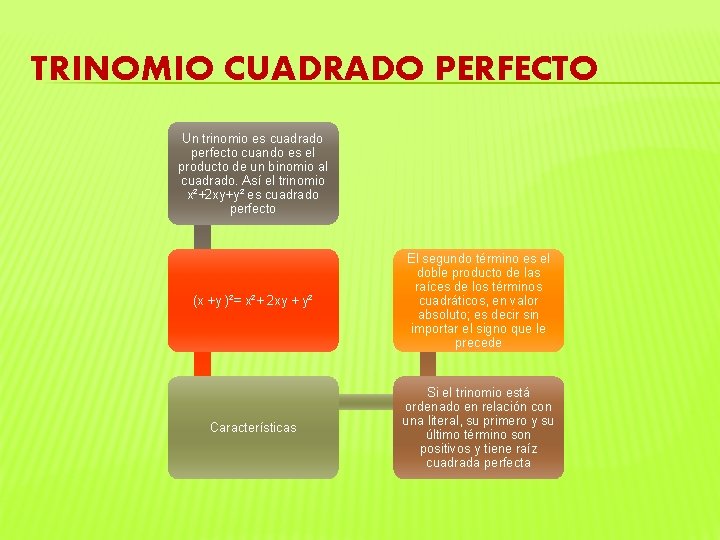
TRINOMIO CUADRADO PERFECTO Un trinomio es cuadrado perfecto cuando es el producto de un binomio al cuadrado. Así el trinomio x²+2 xy+y² es cuadrado perfecto (x +y )²= x²+ 2 xy + y² El segundo término es el doble producto de las raíces de los términos cuadráticos, en valor absoluto; es decir sin importar el signo que le precede Características Si el trinomio está ordenado en relación con una literal, su primero y su último término son positivos y tiene raíz cuadrada perfecta

TRINOMIO DE LA FORMA X²+BX+C Los factores de un trinomio cuadrático de la forma x²+bx+c, no son primos son dos binomios con un término en común, el cuál se obtiene al sacar de la raíz cuadrada al término cuadrático (x²). Los otros dos términos de los binomios son dos números cuyo producto es c y cuya suma es b X²+3 x+10 =(x + 5)(x – 2)

TRINOMIO DE LA FORMA AX²+BX+C Los pasos para factorizar este tipo de trinomio por agrupación son: • Encuentra el producto ac • Encuentra dos números cuyo producto sea ac y cuya suma sea b • Con los números encontrados en el paso anterior; reescribe el término bx como la suma algebraica de dos términos cuyos coeficientes numéricos sean los dos números obtenidos en el segundo paso • Factoriza por agrupación

FACTORIZACIÓN DE SUMA Y DIFERENCIA DE CUBOS Pasos • El primer factor se construye como la suma de las raíces cúbicas de sus términos • El segundo factor se construye sumando los cuadrados de dichas raíces cúbicas, y a dicha suma se le resta el producto de sus bases • x³+ y³= (x + y)(x² - xy + y²) • X³- y³= (x - y)(x² + xy + y²)

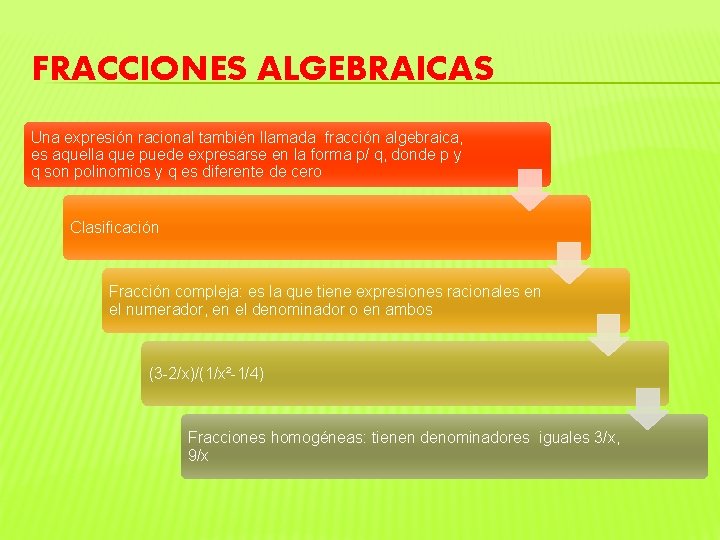
FRACCIONES ALGEBRAICAS Una expresión racional también llamada fracción algebraica, es aquella que puede expresarse en la forma p/ q, donde p y q son polinomios y q es diferente de cero Clasificación Fracción compleja: es la que tiene expresiones racionales en el numerador, en el denominador o en ambos (3 -2/x)/(1/x²-1/4) Fracciones homogéneas: tienen denominadores iguales 3/x, 9/x

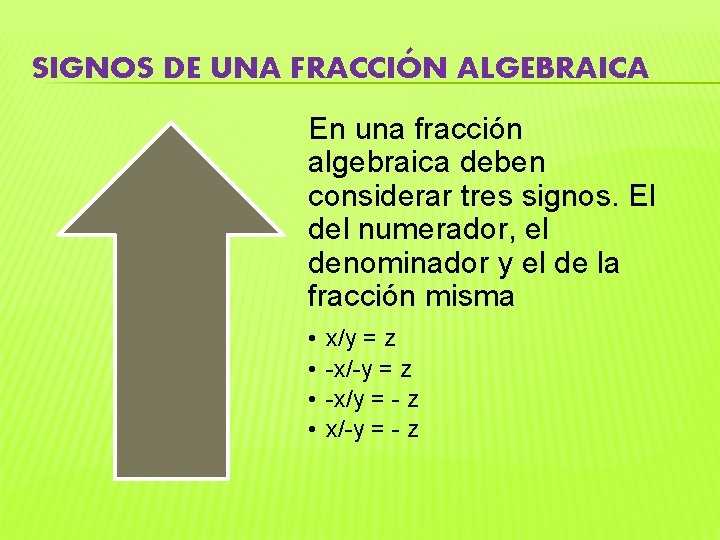
SIGNOS DE UNA FRACCIÓN ALGEBRAICA En una fracción algebraica deben considerar tres signos. El del numerador, el denominador y el de la fracción misma • • x/y = z -x/-y = z -x/y = - z x/-y = - z

OPERACIONES CON EXPRESIONES ALGEBRAICAS RACIONALES Suma y resta de fracciones algebraicas Multiplicación de fracciones algebraicas • Homogéneas: Se suman y o restan sus numeradores y el resultado se divide entren el denominador común, reduciéndose la expresión en caso que sea posible • Heterogéneas: Se multiplica el numerador y el denominador de cada fracción por los factores necesarios para obtener fracciones equivalentes a las originales y que a la vez sea homogéneas entre sí • Antes de efectuar la multiplicaciones señaladas es conveniente factorizar los denominadores, en caso de que sea posible, para tener una mayor claridad en cuanto a las operaciones por realizar. Una vez que las operaciones indicadas queden como sumas o restas de fracciones homogéneas, se procede a efectuar dichas operaciones. • El producto de dos o más fracciones algebraicas es otro cuyo numerador es el producto de dos numeradores y cuyo denominador es el producto de los denominadores • Hay que tener presente que es la expresión racional resulta al multiplicarse dos o más fracciones algebraicas y simplifica el resultado

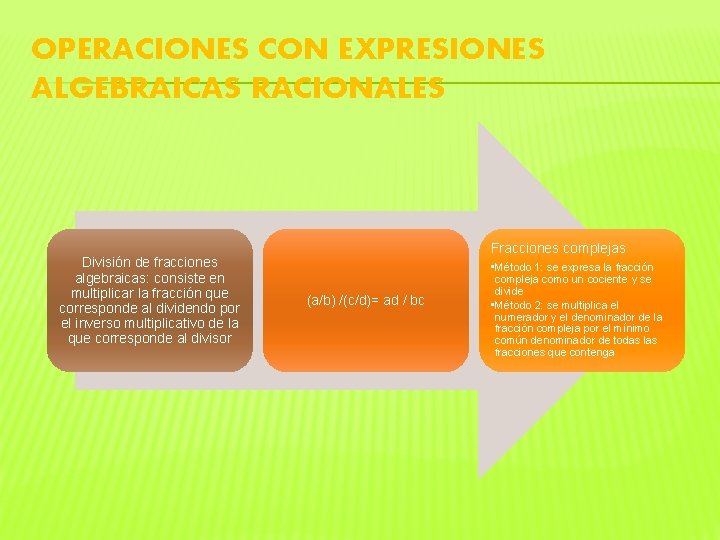
OPERACIONES CON EXPRESIONES ALGEBRAICAS RACIONALES División de fracciones algebraicas: consiste en multiplicar la fracción que corresponde al dividendo por el inverso multiplicativo de la que corresponde al divisor Fracciones complejas (a/b) /(c/d)= ad / bc • Método 1: se expresa la fracción compleja como un cociente y se divide • Método 2: se multiplica el numerador y el denominador de la fracción compleja por el mínimo común denominador de todas las fracciones que contenga

UNIDAD 3 �“Manejo de ecuaciones de primero y segundo grado y funciones algebraicas”

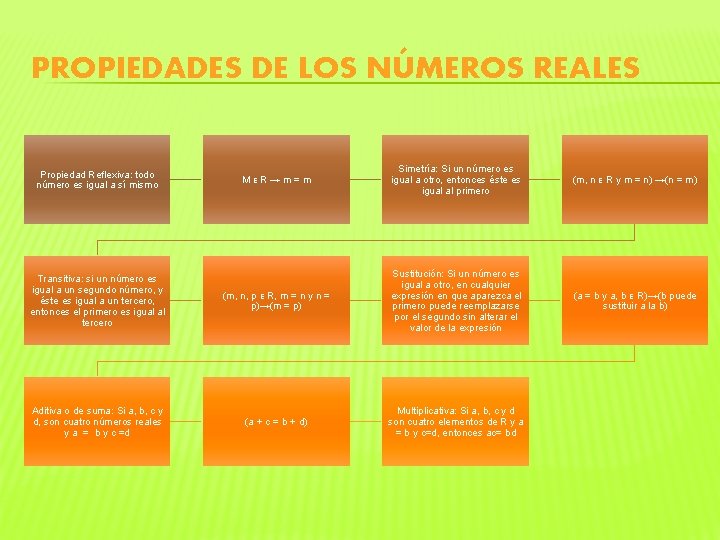
PROPIEDADES DE LOS NÚMEROS REALES MᴇR→m=m Simetría: Si un número es igual a otro, entonces éste es igual al primero (m, n ᴇ R y m = n) →(n = m) Transitiva: si un número es igual a un segundo número, y éste es igual a un tercero, entonces el primero es igual al tercero (m, n, p ᴇ R, m = n y n = p)→(m = p) Sustitución: Si un número es igual a otro, en cualquier expresión en que aparezca el primero puede reemplazarse por el segundo sin alterar el valor de la expresión (a = b y a, b ᴇ R)→(b puede sustituir a la b) Aditiva o de suma: Si a, b, c y d, son cuatro números reales y a = b y c =d (a + c = b + d) Multiplicativa: Si a, b, c y d son cuatro elementos de R y a = b y c=d, entonces ac= bd Propiedad Reflexiva: todo número es igual a sí mismo

POSTULADOS Cerradura: Para la suma: si a y b son elementos de R, entonces la suma también es elemento de R, y a los números a y b les llamamos sumandos • a, b ᴇ R →(a + b) ᴇ R • Para la multiplicación: si a y b son elementos de R entonces el producto también es un elemento de R, y a los números a y b les llamamos factores • a, b ᴇ R →(a • b) ᴇ R Conmutativo • Para la suma: si a y b son números reales, el orden en que se sumen no afecta el resultado a, b ᴇ R→ a + b = b + a • Para la multiplicación: si a y b don números reales el orden en que se multipliquen no afecta al producto • a, b ᴇ R →a • b = b • a Asociativo • Para la suma: si a, b, c, son tres números reales, es igual que a la suma de a y b se le sume la suma de b y c • a, b, c ᴇ R →(a + b) + c = a + (b + c) • Para la multiplicación: si a, b y c son elementos de R, es igual que el producto de a con b se multiplique por c, a que a la a se multiplique por el producto de b con c • a, b, c ᴇ R→(a • b) • c = a • (b • c )

POSTULADOS Distributiva: Identidad Inversos • A la izquierda • Sean a, b, c ᴇ R →a • (b + c) = a • b + a • c • A la derecha • Sean a, b, c ᴇ R →(a + b) • c =a • c+b • c • Para la suma: la suma de cualquier elemento R y el cero es el mismo elemento, por lo que al número cero le llamamos el elemento identidad para la suma • aᴇ R → a + 0 = a • Para la multiplicación: El producto de cualquier elemento de R y el uno es el mismo elemento, entonces, el número uno es el elemento identidad para la multiplicación • aᴇ R →a • 1 = a • El número cero es diferente del número uno: 0≠ 1 • aᴇ R →a + 0 = 0 + a = a, a • 1=1 • a=a • Para la suma: Para todo a ᴇ R existe otro elemento de R: (-a), llamado el inverso para la suma de modo que la suma de los dos es 0 • Para la multiplicación : Para toda a ᴇ R, a ≠ 0, existe otro elemento de R, (1/a), llamado el inverso de la multiplicación de modo que el producto de los dos es 1 • aᴇ R →a + (-a) = 0 a ᴇ R, a ≠ 0 →a • (1/ a) = 1

ECUACIONES Ecuación: igualdad entre dos expresiones matemáticas formadas por datos conocidos e incógnitas (datos desconocidos). Las expresiones separadas por el signo igual (=) recibe el nombre de miembros de la ecuación izquierdo y derecho). El término que no contiene incógnitas recibe el nombre de término independiente y si no aparece es igual a cero. El grado de una ecuación es igual al mayor de los grados de todos los términos que la forman y determinan el número máximo de soluciones de una ecuación. Para calcular el grado de un término se suman los exponentes de todas las incógnitas de que consta una solución de la ecuación es un valor de los que puede tomar la incógnita para la que se cumple la igualdad, es decir, que al sustituir la incógnita por este valor, el miembro izquierdo es igual, o equivalente al miembro derecho.

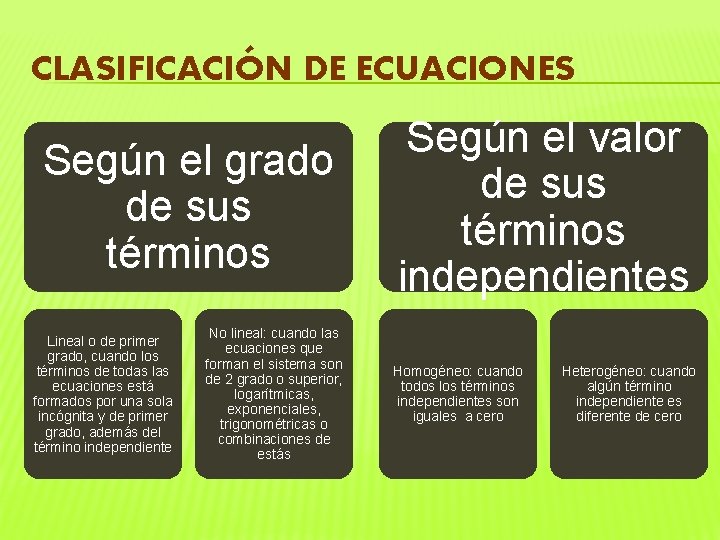
CLASIFICACIÓN DE ECUACIONES Según el número de soluciones se clasifican en: Compatibles: cuando tienen solución Determinadas: cuando tienen un número finito de soluciones Indeterminadas: tienen un número infinito de soluciones Incompatibles: cuando no tienen solución

CLASIFICACIÓN DE ECUACIONES Según el grado de sus términos Lineal o de primer grado, cuando los términos de todas las ecuaciones está formados por una sola incógnita y de primer grado, además del término independiente No lineal: cuando las ecuaciones que forman el sistema son de 2 grado o superior, logarítmicas, exponenciales, trigonométricas o combinaciones de estás Según el valor de sus términos independientes Homogéneo: cuando todos los términos independientes son iguales a cero Heterogéneo: cuando algún término independiente es diferente de cero

ECUACIONES LINEALES Para resolver problema planteados en el lenguaje verbal se recomienda lo siguiente: • Leer el problema con atención para identificar las incógnitas y las cantidades conocidas. • Elegir las letras que se utilizarán para representar las incógnitas del problema • Expresar mediante una ecuación la relación que existe entre los datos del problema • Encontrar el valor o los valores de las incógnitas de la ecuación que resulta del paso anterior • Verificar la solución obtenida

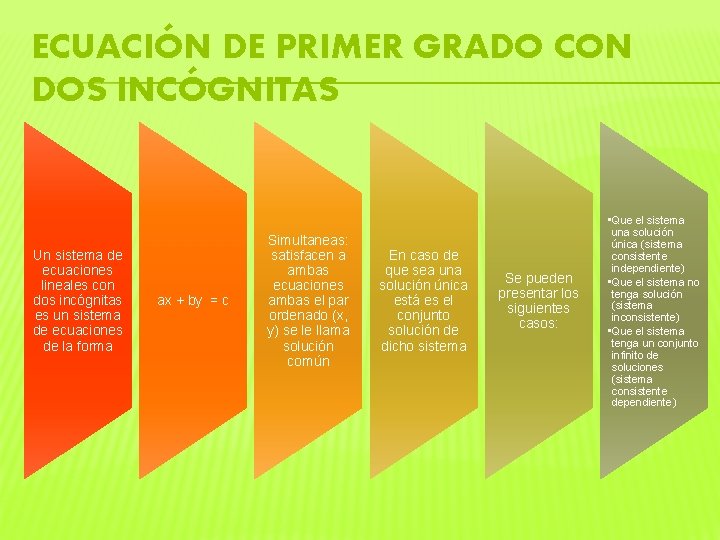
ECUACIÓN DE PRIMER GRADO CON DOS INCÓGNITAS Un sistema de ecuaciones lineales con dos incógnitas es un sistema de ecuaciones de la forma ax + by = c Simultaneas: satisfacen a ambas ecuaciones ambas el par ordenado (x, y) se le llama solución común En caso de que sea una solución única está es el conjunto solución de dicho sistema Se pueden presentar los siguientes casos: • Que el sistema una solución única (sistema consistente independiente) • Que el sistema no tenga solución (sistema inconsistente) • Que el sistema tenga un conjunto infinito de soluciones (sistema consistente dependiente)

SIMULTANEA CON DOS VARIABLES Métodos de solución Suma y resta: Si ha ambos miembros de una igualdad se le suma o restan los de otra igualdad, se obtiene otra igualdad Sustitución: consiste en despejar una de las incógnitas en una de las ecuaciones del sistema en caso de que sea necesario, y después sustituir su expresión equivalente a otra Igualación: Consiste en despejar una misma incógnita en ambas ecuaciones del sistema, después igualar las expresiones equivalentes de ellas y resolver la ecuación obtenida con dicha igualación

MÉTODO DE ELIMINACIÓN (SUMA Y RESTA) Pasos • Se escriben ambas ecuaciones en la forma ax + by = c • Multiplicar una o ambas ecuaciones por un número tal que resulten ecuaciones equivalentes a las originales, que contengan coeficientes con igual valor absoluto en una de las incógnitas y que al sumarlas o restarlas de miembro a miembro resulte una ecuación con una incógnita • Resolver la ecuación con una incógnita que resulta de la suma o diferencia de ecuaciones, con esto se obtiene el valor de las incógnitas • Sustituir el valor determinado en el paso anterior en cualquiera de las ecuaciones originales y resolver está ecuación para determinar el valor de la otra incógnita • Comprobar la solución del problema

MÉTODO DE SUSTITUCIÓN Método de resolución de sistemas de ecuaciones cuya finalidad es obtener un sistema equivalente en el que una de las ecuaciones tenga una incógnita menos. Para ello se despeja una incógnita de una de las ecuaciones y se sustituye en la otra

MÉTODO DE IGUALACIÓN Para obtener el de la otra incógnita se sustituye el valor obtenido de la ecuación anterior en cualquiera de las expresiones donde está la incógnita despejada Al resolver la ecuación que resulta de la igualación de las expresiones equivalentes a la incógnita despejada, se obtiene el valor de la incógnita contenida en ella.

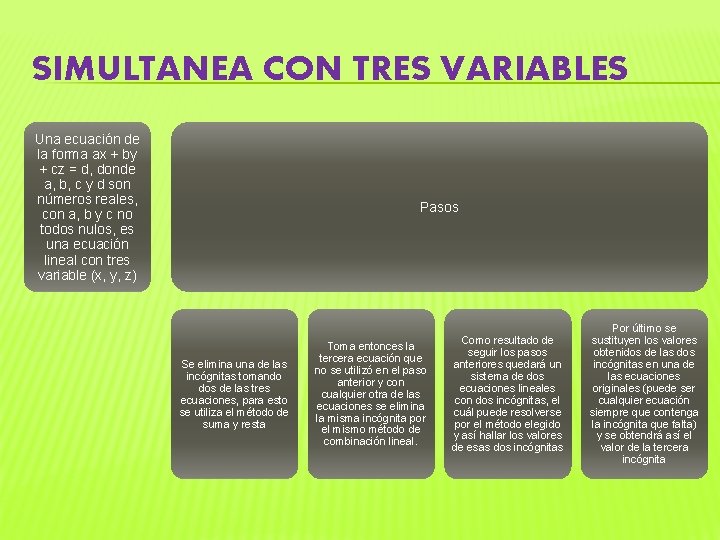
SIMULTANEA CON TRES VARIABLES Una ecuación de la forma ax + by + cz = d, donde a, b, c y d son números reales, con a, b y c no todos nulos, es una ecuación lineal con tres variable (x, y, z) Pasos Se elimina una de las incógnitas tomando dos de las tres ecuaciones, para esto se utiliza el método de suma y resta Toma entonces la tercera ecuación que no se utilizó en el paso anterior y con cualquier otra de las ecuaciones se elimina la misma incógnita por el mismo método de combinación lineal. Como resultado de seguir los pasos anteriores quedará un sistema de dos ecuaciones lineales con dos incógnitas, el cuál puede resolverse por el método elegido y así hallar los valores de esas dos incógnitas Por último se sustituyen los valores obtenidos de las dos incógnitas en una de las ecuaciones originales (puede ser cualquier ecuación siempre que contenga la incógnita que falta) y se obtendrá así el valor de la tercera incógnita

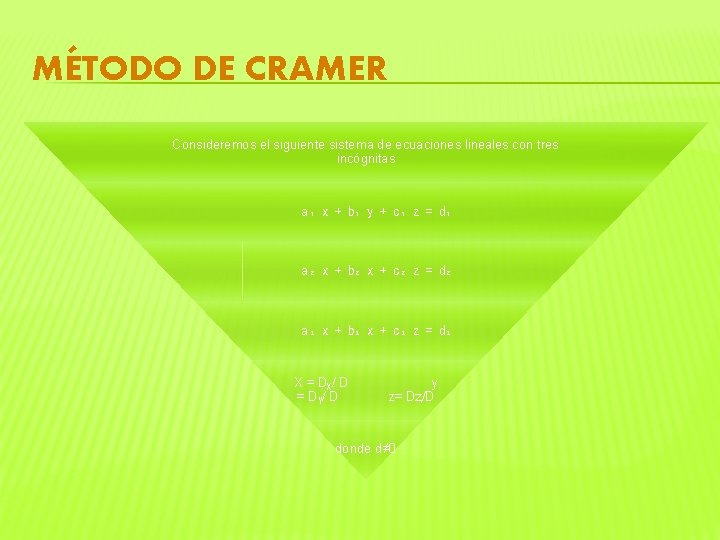
MÉTODO DE CRAMER Consideremos el siguiente sistema de ecuaciones lineales con tres incógnitas a₁ x + b₁ y + c₁ z = d₁ a₂ x + b₂ x + c₂ z = d₂ a₃ x + b₃ x + c₃ z = d₃ X = Dᵪ/ D = Dᵧ/ D y z= Dⱬ/D donde d≠ 0

REGLA DE SARRUS Pasos a seguir • Escribir debajo del tercer renglón los dos primeros renglones • Tracemos tres diagonales de derecha a izquierda y tres en sentido anterior • Hallar cada uno de los productos de los tres números por los que pasa la diagonal • a₁ b₂ c₃ • a₂ b₃ c₁ • a₃ b₁ c₂ • a₁ b₃ c₂ • a₂ b₁ c₃ • Restar la suma de los productos de los números que están colocados en las diagonales trazadas de izquierda a derecha y de arriba hacia abajo • El número que resulta del paso anterior es el número que corresponde al determinante

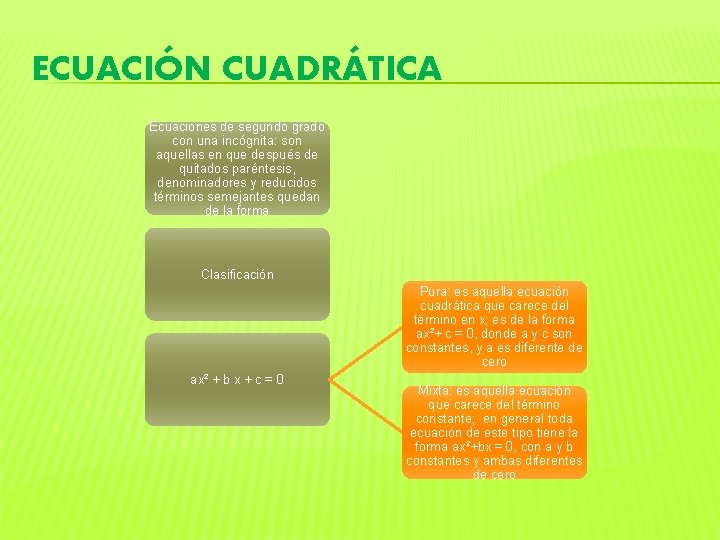
ECUACIÓN CUADRÁTICA Ecuaciones de segundo grado con una incógnita: son aquellas en que después de quitados paréntesis, denominadores y reducidos términos semejantes quedan de la forma Clasificación Pura: es aquella ecuación cuadrática que carece del término en x; es de la forma ax²+ c = 0, donde a y c son constantes, y a es diferente de cero ax² + b x + c = 0 Mixta: es aquella ecuación que carece del término constante; en general toda ecuación de este tipo tiene la forma ax²+bx = 0, con a y b constantes y ambas diferentes de cero

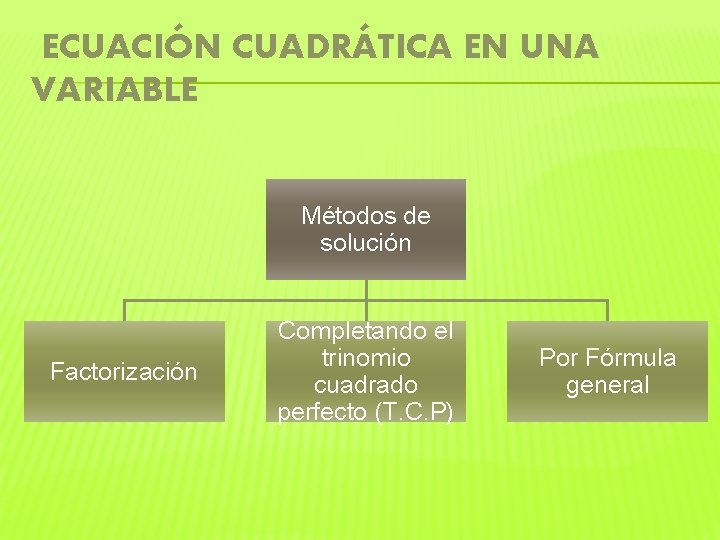
ECUACIÓN CUADRÁTICA EN UNA VARIABLE Métodos de solución Factorización Completando el trinomio cuadrado perfecto (T. C. P) Por Fórmula general

FACTORIZACIÓN Para resolver una ecuación cuadrática por este método se requiere que la ecuación este escrita en su forma general o normal. Consiste en descomponer en factores la expresión ax²+bx+c, igualar cada factor a cero después resolver cada ecuación para x. Las soluciones de las ecuaciones que resultan de igualar a cero cada factor forman el conjunto solución

COMPLETANDO T. C. P. Pasos a seguir • Divide ambos miembros de la ecuación por el coeficiente de x² • Transpón el término constante de la ecuación anterior al segundo miembro (obviamente, con signo contrario) • Suma ambos miembros de la ecuación anterior un número tal que en el miembro izquierdo se forme un trinomio cuadrado perfecto. • Factoriza el trinomio cuadrado perfecto del miembro izquierdo y simplifica el lado derecho de la ecuación • Si el número que aparece en el miembro derecho es positivo , extrae la raíz cuadrada en ambos miembros y resuelve la ecuación con el valor absoluto que resulta

POR FÓRMULA GENERAL La fórmula cuadrática resuelve cualquier ecuación cuadrática. Simplemente identifique a, b y c e inserte esos números en la fórmula. Observe que si b es positiva, entonces –b (el opuesto b) es un número negativo. Si b es negativa, entonces – b es un número positivo

USO DEL DISCRIMINANTE Se sugiere realizar lo siguiente: Si b² - 4 ac = 0, las raíces son reales e iguales Si b² - 4 ac ˂ 0, las raíces no son reales Si b² - 4 ac es un cuadrado perfecto diferente de cero, las raíces son reales, racionales de diferente valor Si b² - 4 ac ˃ 0, pero no es cuadrado perfecto, las raíces son reales, irracionales y de diferente valor

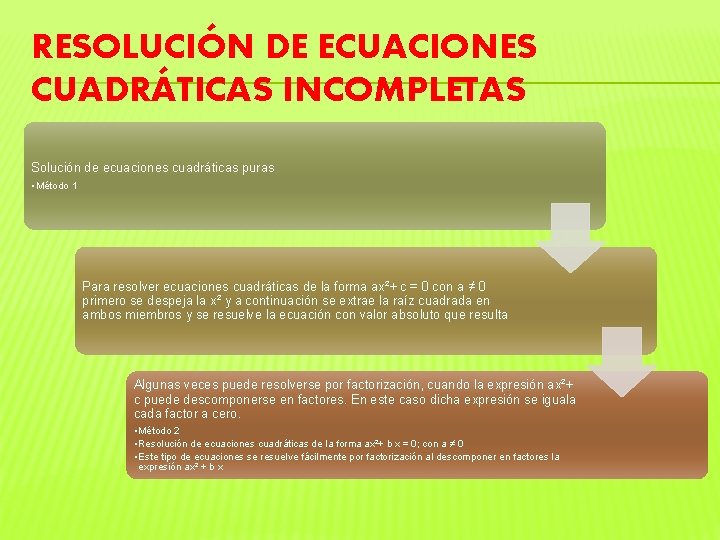
RESOLUCIÓN DE ECUACIONES CUADRÁTICAS INCOMPLETAS Solución de ecuaciones cuadráticas puras • Método 1 Para resolver ecuaciones cuadráticas de la forma ax²+ c = 0 con a ≠ 0 primero se despeja la x² y a continuación se extrae la raíz cuadrada en ambos miembros y se resuelve la ecuación con valor absoluto que resulta Algunas veces puede resolverse por factorización, cuando la expresión ax²+ c puede descomponerse en factores. En este caso dicha expresión se iguala cada factor a cero. • Método 2 • Resolución de ecuaciones cuadráticas de la forma ax²+ b x = 0; con a ≠ 0 • Este tipo de ecuaciones se resuelve fácilmente por factorización al descomponer en factores la expresión ax² + b x

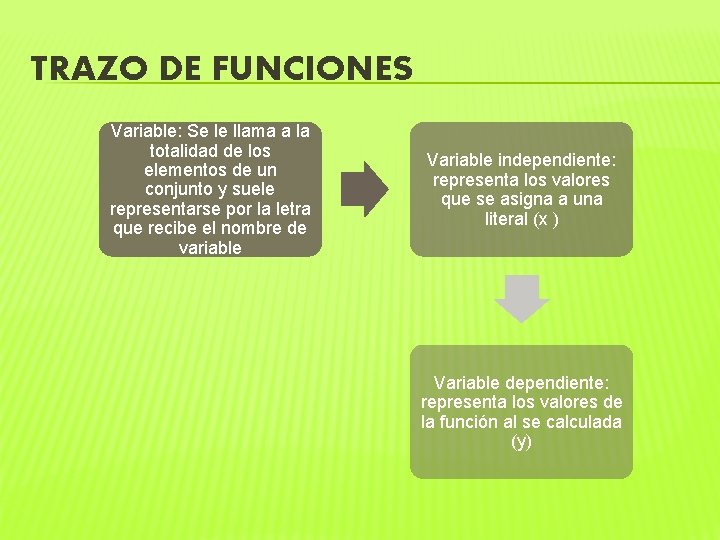
TRAZO DE FUNCIONES Variable: Se le llama a la totalidad de los elementos de un conjunto y suele representarse por la letra que recibe el nombre de variable Variable independiente: representa los valores que se asigna a una literal (x ) Variable dependiente: representa los valores de la función al se calculada (y)

FUNCIONES Aplicación entre dos conjuntos numéricos D e I donde para cada valor del conjunto D le corresponde un único elemento del conjunto I. El conjunto D recibe el nombre de dominio de la función y se simboliza Dom (f). Cualquiera de los elementos del conjunto D se representa por la letra x, que se denomina variable independiente. El conjunto final I se denomina conjunto de imagen de D o recorrido de la función, y se simboliza como Im (f). Cada uno de los elementos del conjunto I se representa por la letra y que es la variable independiente

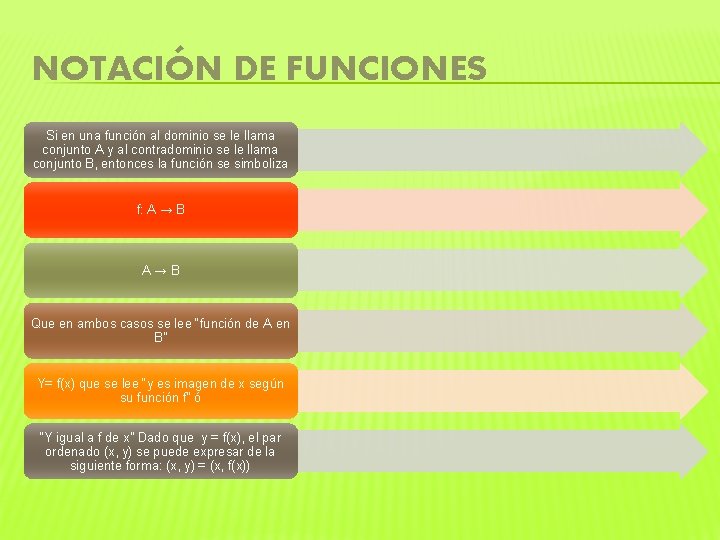
NOTACIÓN DE FUNCIONES Si en una función al dominio se le llama conjunto A y al contradominio se le llama conjunto B, entonces la función se simboliza f: A → B A→B Que en ambos casos se lee “función de A en B” Y= f(x) que se lee “y es imagen de x según su función f” ó “Y igual a f de x” Dado que y = f(x), el par ordenado (x, y) se puede expresar de la siguiente forma: (x, y) = (x, f(x))

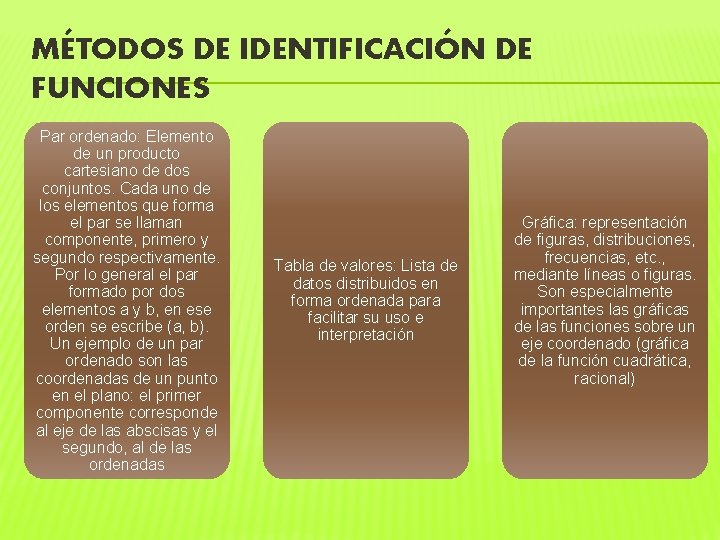
MÉTODOS DE IDENTIFICACIÓN DE FUNCIONES Par ordenado: Elemento de un producto cartesiano de dos conjuntos. Cada uno de los elementos que forma el par se llaman componente, primero y segundo respectivamente. Por lo general el par formado por dos elementos a y b, en ese orden se escribe (a, b). Un ejemplo de un par ordenado son las coordenadas de un punto en el plano: el primer componente corresponde al eje de las abscisas y el segundo, al de las ordenadas Tabla de valores: Lista de datos distribuidos en forma ordenada para facilitar su uso e interpretación Gráfica: representación de figuras, distribuciones, frecuencias, etc. , mediante líneas o figuras. Son especialmente importantes las gráficas de las funciones sobre un eje coordenado (gráfica de la función cuadrática, racional)

SISTEMA DE ECUACIONES LINEALES Sistema de ecuaciones: conjunto de ecuaciones cuyas igualdades se cumplen a la vez para unos determinados valores de las incógnitas. Estos reciben el nombre de soluciones del sistema Solución de ecuaciones método gráfico Lineales Simultaneas con dos variables Cuadrática

LINEALES Para poder resolver un sistema de ecuaciones lineales por el método gráfico primero se localizan los pares ordenados en un sistema de coordenadas cartesiana Para localizar un punto P(x, y) en un sistema de coordenadas cartesianas, se traza a partir de dicho punto una línea punteada perpendicular al de las x, y el número le corresponde al punto donde interseca dicho eje representa un valor de la abscisa (x), de igual manera, a partir del punto P se traza una línea perpendicular al eje de las y, y el número que corresponde a la lectura del punto donde se interseca dicho eje representa la ordenada (x)

LINEALES SIMULTANEAS CON DOS VARIABLES La gráfica de una ecuación de la forma a x + b y =c es una recta. Una recta queda determinada si se conocen dos de sus puntos, para representar gráficamente una ecuación lineal con dos variable basta con encontrar dos de sus soluciones y trazar la recta que pasa por los puntos que representa. Para resolver el sistema de ecuaciones con dos incógnitas, por el método gráfico, hay que trazar las gráficas (rectas) de cada ecuación en un sistema de coordenadas cartesiano y su conjunto solución estará formado por pares ordenados (x, y) comunes a ambas rectas

GRÁFICA DE LA FUNCIÓN CUADRÁTICA Cualquier número real puede usarse en lugar de x en f(x) = ax²+bx+c. Por lo tanto, el dominio (el conjunto de coordenadas x) de cualquier función cuadrática es el conjunto de todos los números reales, (- infinito, infinito). El rango (el conjunto de coordenadas y) puede determinarse a partir de la gráfica. Todas las funciones cuadráticas tienen gráficas de forma similar. La gráfica de cualquier función cuadrática recibe el nombre de parábola Una parábola se abre hacia arriba cuando a˃0 Una parábola se abre hacia abajo cuando a˂0 Y= ax²+bx+c