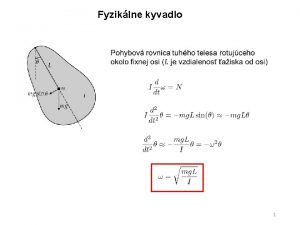
Kmity a vlny 1 Osciltor x Rovnovna poloha













































![Plot[10^(-11)x^4(x-L/2)^10(x-L)^4, {x, 0, L}] 56 Plot[10^(-11)x^4(x-L/2)^10(x-L)^4, {x, 0, L}] 56](https://slidetodoc.com/presentation_image_h/193f03cb40d1a3de236ad218a54baac3/image-56.jpg)


- Slides: 58

Kmity a vlny 1

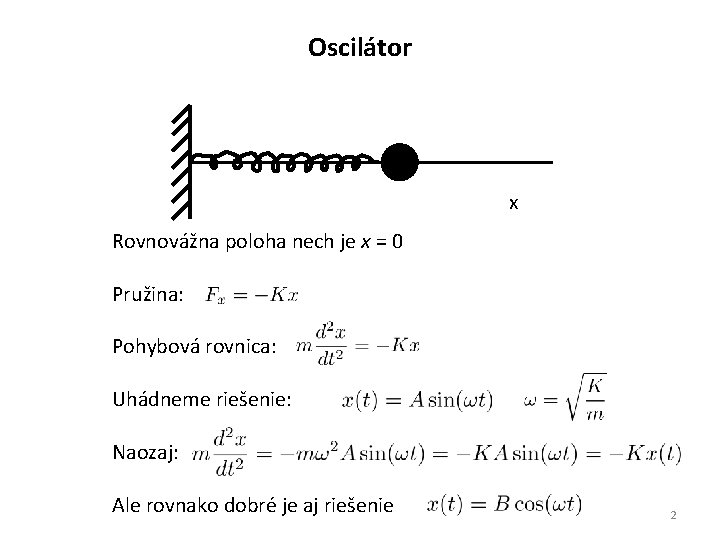
Oscilátor x Rovnovážna poloha nech je x = 0 Pružina: Pohybová rovnica: Uhádneme riešenie: Naozaj: Ale rovnako dobré je aj riešenie 2

Rovnica je tzv. lineárna, čo znamená, že súčet jej dvoch riešení je tiež riešením, teda aj riešenie Pri zadaných počiatočných podmienkach pohyb je periodický s periódou naozaj: 3

Pri ľubovoľných počiatočných podmienkach vieme teda jednoznačne predpovedať budúcnosť, takže sme zrejme našli v tvare (#) všetky riešenia pohybovej rovnice. Lebo ak by boli nejaké ďalšie, potom by budúcnosť už nebola jednoznačná. Čo fyzikálne neočakávame. Je na matematikoch aby naozaj dokázali, že sú to všetky riešenia. Tým sa tu zaoberať nebudeme. Riešenia sme proste uhádli a našli sme ich tak dosť. Ešte trochu iné ekvivalentné vyjadrenie. Označme potom existuje číslo δ že vzťah (#) môžeme zapísať ako stačí nájsť také δ, aby platilo teda 4

Pri ľubovoľných počiatočných podmienkach vieme predpovedať budúcnosť, takže sme zrejme našli v tvare atan 2 je programátorské značenie, ktoré matematici nepoznajú, (#) obor hodnôt funkcie atan 2 je totiž (-π, π), kým obor hodnôt všetky riešenia pohybovej rovnice. Lebo ak by boli nejaké ďalšie, inverznej funkcie k tangensu, arctan() je (-π/2, π/2) potom by budúcnosť už nebola jednoznačná. Čo fyzikálne Funkcia atan 2 je totiž definovaná nie ako inverzná funkcia k neočakávame. Je na matematikoch aby naozaj dokázali, že sú to tangensu ale ako polárny uhol ϕ bodu s kartézskymi súradnicami všetky riešenia. Tým sa tu zaoberať nebudeme. Riešenia sme (x, y), teda taký uhol, že platí proste uhádli a našli sme ich tak dosť. Ešte trochu iné ekvivalentné vyjadrenie. Označme potom existuje číslo δ že vzťah (#) môžeme zapísať ako stačí nájsť také δ, aby platilo teda 5

Teraz urobíme malý trik s komplexnými číslami, využijeme Eulerov vzťah Na označenie imaginárnej jednotky sme použili nezvyklý symbol V matematike sa používa obyčajné i, ale chceme sa vyhnúť zmätkom, keď často budeme používať index i alebo označíme elektrický prúd ako i. môžeme zapísať ako Fakt, že treba zobrať len reálnu časť komplexného čísla často nepíšeme explicitne a píšeme len ako keby výchylka bola komplexné číslo 6

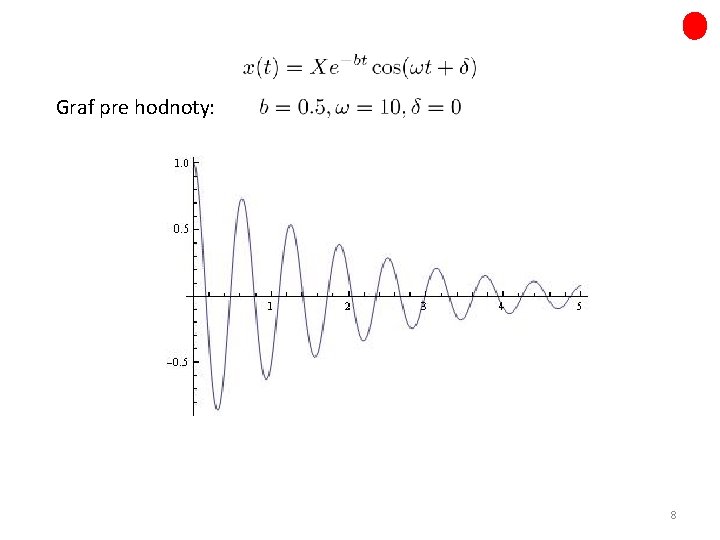
Lineárny oscilátor s tlmením Nech proti pohybu pôsobí odpor prostredia úmerný rýchlosti ale proti smeru rýchlosti, teda sila v tvare (bodka nad písmenom značí prvú deriváciu podľa času, dve bodky druhú deriváciu podľa času). Pohybová rovnica potom bude Všimnime si, že v pohybovej rovnici sú dve časové škály: konštanty aj majú rovnaký fyzikálny rozmer . Predpokladajme Hľadajme riešenie v tvare Dostaneme: 7

Graf pre hodnoty: 8

9

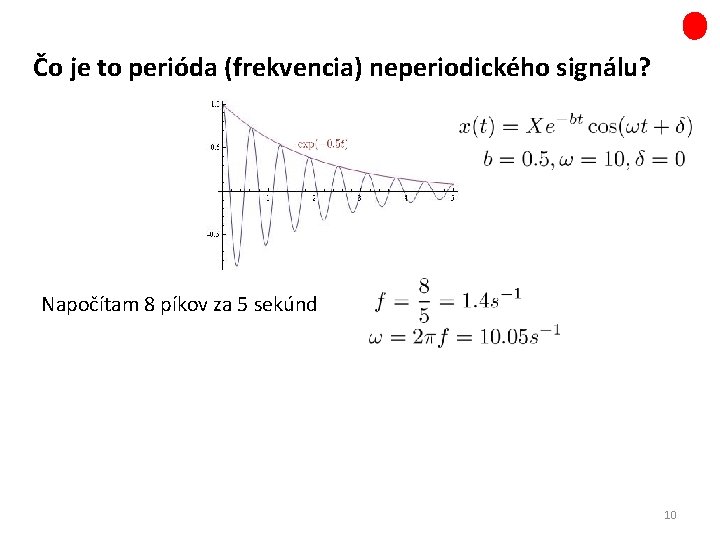
Čo je to perióda (frekvencia) neperiodického signálu? Napočítam 8 píkov za 5 sekúnd 10

Čo je to perióda (frekvencia) neperiodického signálu? ? Napočítam 8 píkov za 5 sekúnd 11

Čo je to perióda (frekvencia) neperiodického signálu? ? Napočítam 8 píkov za 5 sekúnd O poslednom píku nemám istotu, preto Keby som rátal píky nie počas 5 sekúnd ale počas 50 sekúnd, naivne by som čakal, že dostanem 12

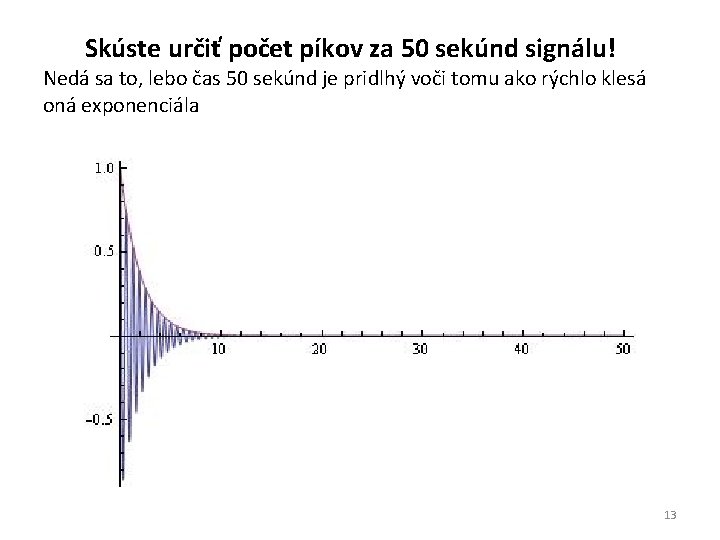
Skúste určiť počet píkov za 50 sekúnd signálu! Nedá sa to, lebo čas 50 sekúnd je pridlhý voči tomu ako rýchlo klesá oná exponenciála 13

Ako rýchlo klesá exponenciála? Za dobu exponenciála už viditeľne poklesne, za dobu poklesne tak, že sa už píky ďalej rátať nedajú 14

Chyba (nepresnosť) určenia frekvencie je teda Rádovo teda platí čosi, čo sa zvykne volať „princíp neurčitosti“ Absolútna chyba určenia frekvencie krát doba prítomnosti 15 signálu je rádovo rovná jednej

Retiazka oscilátorov 16

Zdá sa, že taká intuícia vyžaduje priam genialitu, o niečo neskôr uvidíme, že je pomerne ľahké niečo také si vyhútať. 17

18

19

x=Δ x=2Δ L=NΔ x=iΔ x=(N-1)Δ 20

21

Malá matematická vsuvka V matematike mávame funkcie aj niekoľkých premenných, ako tu Takúto funkciu môžeme derivovať podľa niektorej z jej premenných, pričom ostatné premenné, podľa ktorých nederivujeme, budeme považovať za konštantné (akoby za parametre) teda napríklad definujeme Aby sme upozornili na to, že derivujeme len podľa jednej premennej, kým ostatné sú konštantné, používame v symbole derivácie znak δ namiesto d. Volá sa to parciálna derivácia. Analogicky budeme značiť vyššie parciálne derivácie. 22

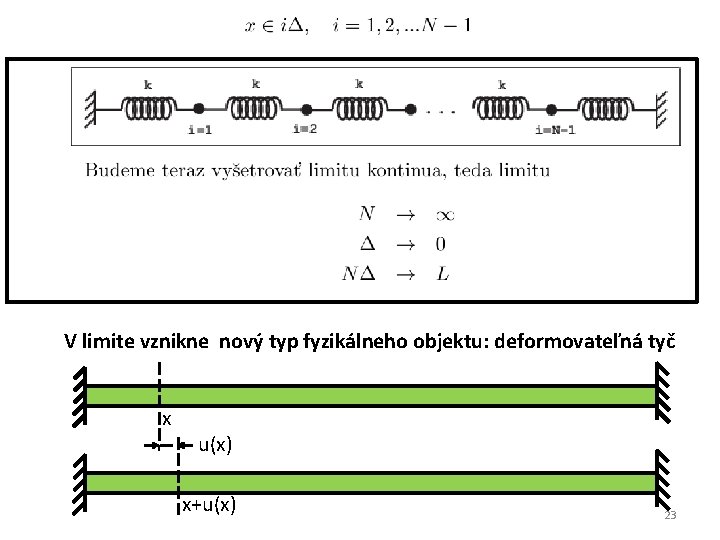
V limite vznikne nový typ fyzikálneho objektu: deformovateľná tyč x u(x) x+u(x) 23

24

25

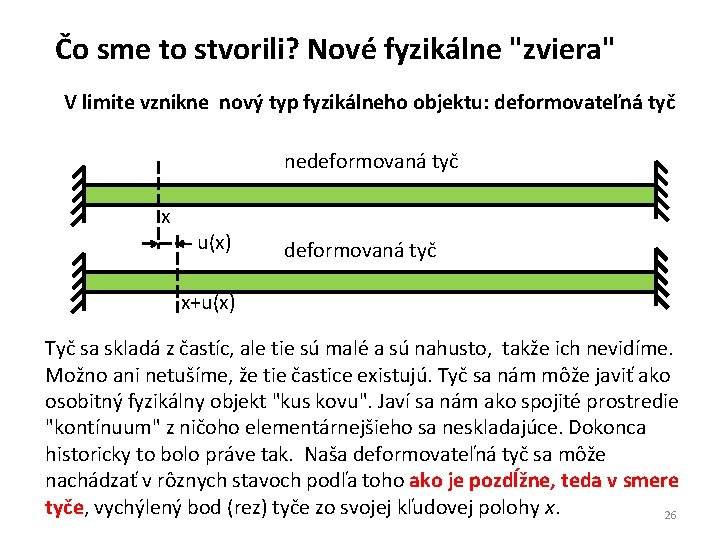
Čo sme to stvorili? Nové fyzikálne "zviera" V limite vznikne nový typ fyzikálneho objektu: deformovateľná tyč nedeformovaná tyč x u(x) deformovaná tyč x+u(x) Tyč sa skladá z častíc, ale tie sú malé a sú nahusto, takže ich nevidíme. Možno ani netušíme, že tie častice existujú. Tyč sa nám môže javiť ako osobitný fyzikálny objekt "kus kovu". Javí sa nám ako spojité prostredie "kontínuum" z ničoho elementárnejšieho sa neskladajúce. Dokonca historicky to bolo práve tak. Naša deformovateľná tyč sa môže nachádzať v rôznych stavoch podľa toho ako je pozdĺžne, teda v smere tyče, vychýlený bod (rez) tyče zo svojej kľudovej polohy x. 26

Tu je video experimentu demonštrujúce ako možno presúvaním prstov pozdĺž tyče vzbudiť pozdĺžne deformácie, ktorých časový vývoj sa potom prejaví ako zvuk. Všimnite si koniec videa. Plastový pohár fungujúci ako rezonátor, nezosilní zvuk tyče, ak je k tyči priložený priečne, ale zosilní zvuk pri pozdĺžnom priložení. To dokazuje, že zvukové vlny šíriace sa v tyči sú 27 pozdĺžne.

x u(x) x+u(x) Predstierajme teda, že nevieme, že sa tyč skladá z častíc a naučme sa robiť fyziku tyče ako osobitného druhu fyzikálneho objektu. Volá sa to "efektívna teória" alebo efektívny prístup. Efektívne teórie používame vlastne denne, len si to neuvedomujeme. Hovoríme, že z vodovodu tečie "voda", ako keby "voda" bol osobitný fyzikálny systém (objekt). V skutočnosti nič také ako "voda" vlastne neexistuje. Z vodovodu tečie kopa protónov, neutrónov a elektrónov. Ale keby sme chceli stavať priehradu a tečenie "vody" chceli popisovať ako presúvanie protónov, elektrónov a neutrónov, asi by sme sa zbláznili. Namiesto toho používame efektívny pojem "voda" a popisujeme jej 28 vlastnosti pomocou pojmov ako "hustota" alebo "viskozita".

A nie je to tak dávno, čo sme prišli na to, že aj popis "vody" ako systému protónov, elektrónov a neutrónov je tiež len efektívny popis, hoci hlbšej úrovne. V skutočnosti je to systém kvarkov, gluónov, fotónov, elektrónov a ešte nejakých ďalších častíc. A kto vie, či o pár rokov nezistíme, že aj elektrón je len efektívny pojem. 29

x u(x) x+u(x) Takže budeme skúmať tyč v priblížení efektívnej teórie, považujúc ju za jednorozmerné kontínuum Ako s každým fyzikálnym systémom, musíme sa naučiť • ako sa popíše okamžitý stav systému • ako sa predpovedá budúcnosť, teda časový vývoj stavov Stav nášho jednorozmerného kontínua v istom okamihu poznáme ak zadáme funkciu deformácie (posunutia každého bodu tyče) a ešte aj jej prvú časovú deriváciu v uvažovanom okamihu Že treba zadávať aj časovú deriváciu uvidíme z toho, že pohybová rovnica 30 je druhého rádu podobne ako Newtonova.

Takže pozor: zadať stav častice v nejakom okamihu sme vedeli pomocou (iba) 6 čísel: tri zložky vektoru polohy a tri zložky vektoru rýchlosti Na zadanie stavu tyče potrebujeme "dvakrát spojite nekonečne veľa čísel" teda potrebujeme zadať hodnoty funkcie a aj jej prvej časovej derivácie Budúcnosť budeme predpovedať pomocou rovnice, ktorú sme našli, teda toto je vlastne spojite nekonečne veľa diferenciálnych rovníc, po jednej pre každé Rovnice ale nie sú navzájom nezávislé. Cez pravé strany sa cítia. 31

(#) Zdanlivo sú rovnice nezávislé, veď v každej rovnici je len „jedno x“. Takže sa to zdanlivo podobá na pohybové rovnice Newtonovho typu Ibaže výraz na pravej strane sa týka nie jedného bodu x ale troch infinitezimálne blízkych bodov Druhá derivácia „cíti“ zakrivenie grafu funkcie. Na to potrebuje poznať hodnotu funkcie v troch infinitezimálne blízkych bodoch (kým prvá derivácia, ktorá „meria“ strmosť dotyčnice potrebuje hodnoty funkcie v dvoch infinitezimálne blízkych bodoch). Vidno to z pôvodne diskrétneho výrazu Rovníc (#) je teda spojite nekonečne veľa a každá z nich „cíti“ aj predchádzajúcu rovnicu aj nasledujúcu rovnicu. Nemôžeme ich riešiť ako jednu po druhej, riešime ich ako „jednu parciálnu diferenciálnu rovnicu“. 32

Vlnová rovnica: ako predpovedáme budúcnosť Máme zadaný stav v okamihu t=0, teda poznáme funkciu deformácie (posunutia každého bodu tyče) a ešte aj jej prvú časovú deriváciu v uvažovanom okamihu Úlohou je nájsť funkciu Pre (všetky) neskoršie časy t. Zaveďme ešte prirodzené označenie 33

Vlnová rovnica: jednoduché numerické riešenie Toto sú rovnice, ktoré ukazujú ako sa u(t, x), v(t, x) budú po malých krokoch posúvať dopredu v čase, porovnaj s Newtonom 34

Jednoduché numerické riešenie: program Problém musím diskretizovať int imax = 1000; int jmax=1000; //diskretizacia priestoru a casu double Delta=0. 01; double delta=0. 01; //krok v priestore a case //deklarujem polia do ktorych budem ukladat riesenie double [][] u = new double [jmax+1][imax+1]; double [][] v = new double [jmax+1][imax+1]; for(int i=0; i<imax; i++) u[0][i] = U(i*Delta); //kopirovanie pociat. podm. for(int i=0; i<imax; i++) v[0][i] = V(i*Delta); //kopirovanie pociat. podm. for(int j=1; j<=jmax; j++){ //cyklus posuvania v case u[j], [0]=0; u[j][imax]=0; v[j][0]=0; v[j][imax]=0; //okrajove body stoja for(int i=1; i<imax; i++){ //cyklus prebehnutia priestorom vo fixnom case u[j][i]=u[j-1][i]+delta*v[j-1][i]; v[j][i]=v[j-1][i]+delta*c 2*(u[j-1][i-1]-2. *u[j-1][i]+u[j-1][i+1])/Delta } } //Teraz uz mam v poli u[][] napocitane vsetky hodnoty riesenia 35

Matematická vsuvka: Fourierov rozvoj Pre Fourierove sinsusovky platí 36

Vlnová rovnica: analytické riešenie Geniálny Fourierov nápad: hľadajme riešenie v tvare Po dosadení do vlnovej rovnice dostaneme Z jednoznačnosti Fourierovho rozkladu dostaneme rovnice Sú to rovnice nezávislých harmonických oscilátorov 37

všeobecné riešenie má tvar 38

a potom už ľahko vyjadríme riešenie vlnovej rovnice so zadanými okrajovými a počiatočnými podmienkami ako Štandardne sa ešte zavádza označenie takže dostaneme 39

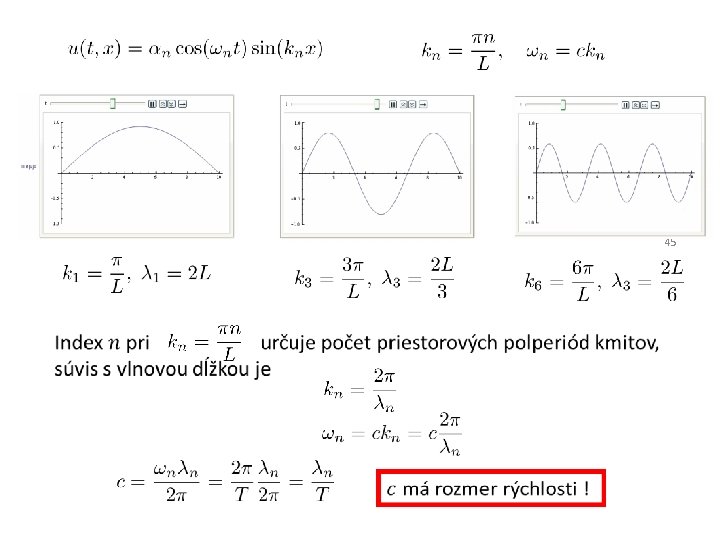
Vlnová rovnica: charakter riešení Vyšetrime vlastnosti najjednoduchšieho riešenia 40

41

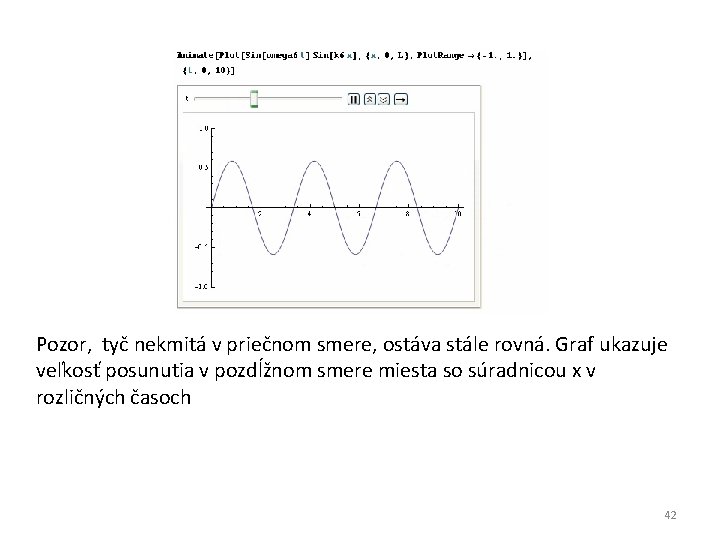
Pozor, tyč nekmitá v priečnom smere, ostáva stále rovná. Graf ukazuje veľkosť posunutia v pozdĺžnom smere miesta so súradnicou x v rozličných časoch 42

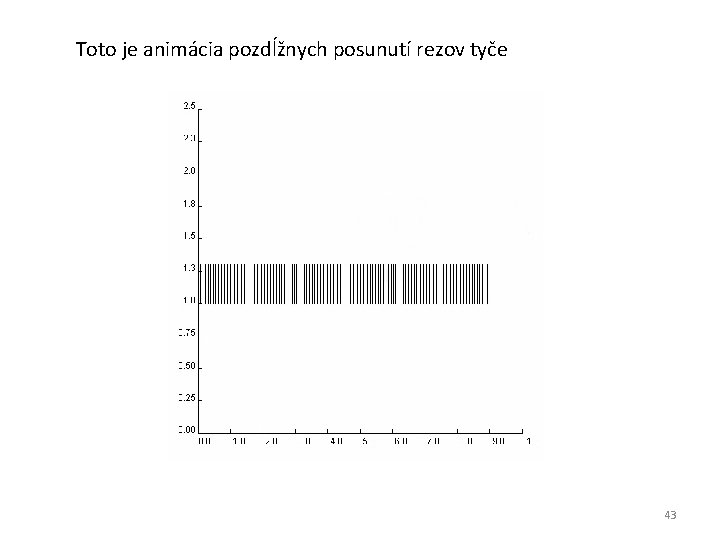
Toto je animácia pozdĺžnych posunutí rezov tyče 43

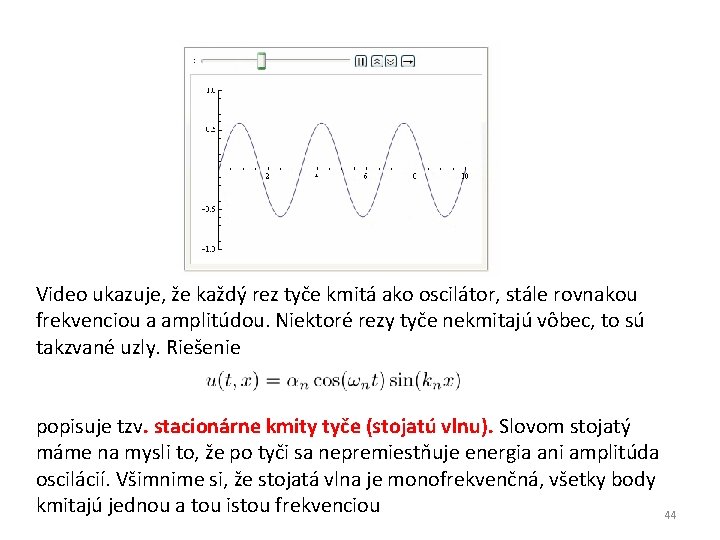
Video ukazuje, že každý rez tyče kmitá ako oscilátor, stále rovnakou frekvenciou a amplitúdou. Niektoré rezy tyče nekmitajú vôbec, to sú takzvané uzly. Riešenie popisuje tzv. stacionárne kmity tyče (stojatú vlnu). Slovom stojatý máme na mysli to, že po tyči sa nepremiestňuje energia ani amplitúda oscilácií. Všimnime si, že stojatá vlna je monofrekvenčná, všetky body kmitajú jednou a tou istou frekvenciou 44

45

Ukážka nestacionárneho vlnenia Na videu je pohybujúca sa vlna 46

Ukážka nestacionárneho vlnenia Na videu je pohybujúca sa vlna Pri špeciálnej počiatočnej podmienke tvaru Fourierovej sínusovky vznikne stojaté (stacionárne) kmitanie. Pri všeobecnej počiatočnej podmienke vznikne postupné (šíriace sa) vlnenie 47

Všimnime si, že platí = 48

Fourierova stojatá vlna vzniká teda superpozíciou dvoch postupných vĺn, jednej šíriacej sa zľava doprava a druhej šíriacej sa sprava doľava. Tie postupné vlny majú v tomto prípade veľmi špeciálny tvar, takže sa poskladajú na stojatú vlnu. Použitím identít pre súčiny trigonometrických funkcií možno ľubovoľné riešenie vlnovej rovnice napísať ako superpozíciu dvoch postupných vĺn, jednej šíriacej sa zľava doprava a druhej šíriacej sa sprava doľava. Tie postupné vlny ale všeobecne nemajú taký špeciálny tvar, aby sa poskladali na stojatú vlnu. Spravidla sa poskladajú na vlnenie striedavo sa pohybujúce zľava doprava, po odraze od konca sprava doľava a po ďalšom odraze zase zľava doprava. . . Videli sme to na videu. 49

Vlnová rovnica Majme ľubovoľnú funkciu jednej premennej a vyrobme z nej funkciu dvoch premenných t, x takto Rovno vidím, že takáto funkcia spĺňa vlnovú rovnicu a podobne ju spĺňa aj funkcia kde je (iná) ľubovoľná funkcia jednej premennej 50

Nemôžem si ale myslieť, že mnou hľadanú funkciu deformácie budem písať ako Lebo funkcia deformácie musí okrem vlnovej funkcie spĺňať aj okrajové podmienky Skúsme ale hľadať riešenie v tvare a nájdime, aké podmienky musia spĺňať (inak ľubovoľné) funkcie , aby boli identicky splnené okrajové podmienky 51

Dostaneme Takže funkcie f a g spolu súvisia takto máme teda teraz podmienka Zjavne je treba použiť periodickú funkciu s periódou , napríklad 52

Potom dostaneme Vo všeobecnosti môžeme použiť ľubovoľnú superpozíciu takých riešení (v časovej závislosti môže byť aj sinus), takže dostávame inou cestou to, čo už poznáme. 53

Zhrňme naše poznatky o vlnovej rovnici s okrajovými podmienkami Všeobecné riešenie môžme písať v tvare superpozície špefciálnych stacionárnych riešení Stacionárne riešenia sú • monofrekvencčné • tvoria úplný systém, teda každé riešenie sa dá písať ako ich superpozícia • sú „ortogonálne“, takže platí túto vlastnosť využívame pri hľadaní koeficientov rozvoja z počiatočných podmienok 54

55
![Plot1011x4xL210xL4 x 0 L 56 Plot[10^(-11)x^4(x-L/2)^10(x-L)^4, {x, 0, L}] 56](https://slidetodoc.com/presentation_image_h/193f03cb40d1a3de236ad218a54baac3/image-56.jpg)
Plot[10^(-11)x^4(x-L/2)^10(x-L)^4, {x, 0, L}] 56

57

58
 Rovnice postupné vlny
Rovnice postupné vlny Pozdlzne vlnenie
Pozdlzne vlnenie Rovnica postupnej mechanickej vlny
Rovnica postupnej mechanickej vlny Izotropné prostredie
Izotropné prostredie Rovnica postupnej mechanickej vlny
Rovnica postupnej mechanickej vlny Kotouč otáčivý kolem osy se nazývá
Kotouč otáčivý kolem osy se nazývá Geografická poloha sydney
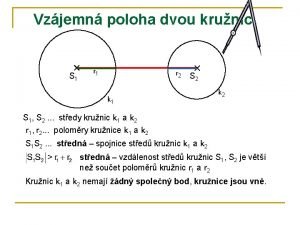
Geografická poloha sydney Vzájemná poloha dvou kružnic
Vzájemná poloha dvou kružnic Blumbergovo znamení
Blumbergovo znamení Průnik dvou rovin
Průnik dvou rovin Argentina poloha
Argentina poloha Autotransfuzni poloha
Autotransfuzni poloha Vzájemná poloha tří rovin
Vzájemná poloha tří rovin Poloha polska
Poloha polska Norsko poloha
Norsko poloha Rovnovážná poloha tělesa
Rovnovážná poloha tělesa Dotyčnica sečnica nesečnica
Dotyčnica sečnica nesečnica Poloha indie
Poloha indie Znak polohy
Znak polohy Indiánský sed poloha
Indiánský sed poloha Nesečnica
Nesečnica Mapa afriky vodstvo
Mapa afriky vodstvo Poloha asie
Poloha asie štrkovka leopoldov
štrkovka leopoldov Taliansko vodstvo
Taliansko vodstvo Pravidelný osemsten
Pravidelný osemsten Vzájomná poloha priamok v rovine
Vzájomná poloha priamok v rovine Poloha savany
Poloha savany Rozloha slovenska
Rozloha slovenska Poloha amazonka
Poloha amazonka Rovnovážná poloha
Rovnovážná poloha Poloha dvou kružnic
Poloha dvou kružnic Antitrendelenburgova poloha
Antitrendelenburgova poloha Subnasale
Subnasale Podvn
Podvn Poloha srdca
Poloha srdca Nesečnica
Nesečnica Mys nordkinn mapa
Mys nordkinn mapa Ortopnoická poloha
Ortopnoická poloha Taliansko poloha
Taliansko poloha Autotransfuzni poloha
Autotransfuzni poloha Vzajomna poloha 2 priamok v priestore
Vzajomna poloha 2 priamok v priestore Poloha znak
Poloha znak Cervikometrie tabulka
Cervikometrie tabulka Průčelná poloha
Průčelná poloha Vzájemná poloha dvou kružnic
Vzájemná poloha dvou kružnic Vzájomná poloha priamky a roviny
Vzájomná poloha priamky a roviny Praktick
Praktick Gastroduodenoskopie
Gastroduodenoskopie Pmka
Pmka Okrajove body slovenska
Okrajove body slovenska Genukubitální poloha
Genukubitální poloha Podnebie australia
Podnebie australia Obrátená trendelenburgova poloha
Obrátená trendelenburgova poloha Nautický trojúhelník
Nautický trojúhelník Antarktida poloha
Antarktida poloha Shautova poloha
Shautova poloha Indiánský sed poloha
Indiánský sed poloha