Introduo aos Conjuntos Difusos INCERTEZA aleatoriedade x impreciso

Introdução aos Conjuntos Difusos • INCERTEZA: aleatoriedade x imprecisão • CONJUNTOS CLÁSSICOS: caracterização • CONJUNTOS DIFUSOS: caracterização Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Clássicos: caracterização DEFINIÇÃO: elemento, propriedade e função característica. • CONCEITOS: cardinalidade, complemento, união e intersecção. • PROPRIEDADES DE OPERAÇÕES: involução, comutatividade, associatividade, distributividade, idempotência, absorção, identidade. • LEIS: contradição, meio excluído, Morgan • OUTRAS PROPRIEDADES: conjuntos disjuntos, partição. Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Difusos: caracterização • • • CONJUNTO: Difuso/Nebuloso/Fuzzy FUNÇÃO DE PERTINÊNCIA NOTAÇÃO DE UM CONJUNTO DIFUSO PROPRIEDADES: α-cut, suporte, núcleo, altura, convexidade OPERAÇÕES-PADRÃO: complemento, união (t-conorma), intersecção (t-norma) • TIPOS DE CONJUNTOS DIFUSOS: ordinário e intervalorado. Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

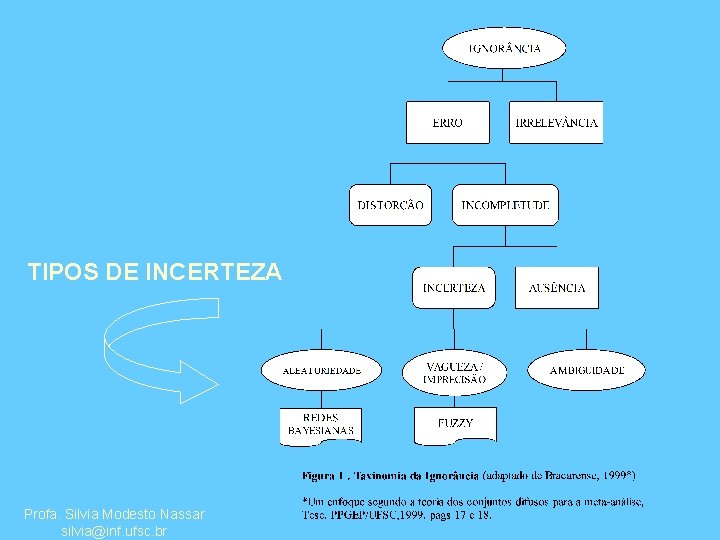
TIPOS DE INCERTEZA Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

INCERTEZA: aleatoriedade x imprecisão(vagueza) • Incerteza: “o elemento x é membro do conjunto A” F aleatoriedade : probabilidade de ocorrer o conjunto A a proposição ou é V (certamente x pertence ao conjunto A) ou é F (certamente x não pertence ao conjunto A) distinção precisa, não ambígua, entre ser membro ou não do conjunto A Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Incerteza: aleatoriedade x imprecisão • Incerteza: “o elemento x é membro do conjunto A” F imprecisão : grau de pertinência ao conjunto fuzzy A esta proposição NÃO necessariamente é V ou F pode ser Verdadeira somente com algum grau, o grau em que x é membro de A A é um conjunto fuzzy se seus limites não são precisos. Assim, a pertinência a um conjunto fuzzy não é uma afirmação ou negação, mas uma intensidade de pertinência. Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos: Clássicos x Difusos • Conjuntos Clássicos: F limites precisos F pertence ou não pertence F a transição de pertencer a não pertencer é brusca Profa. Silvia Modesto Nassar silvia@inf. ufsc. br • Conjuntos difusos: F limites imprecisos F grau de pertinência F expressam a transição gradual de pertencer a não pertencer F representam conceitos vagos expressos em linguagem natural

Conjunto A: { homem careca } • Abordagem Clássica: F PROBABILIDADE de ocorrência do conjunto A: [0; 1] Profa. Silvia Modesto Nassar silvia@inf. ufsc. br • Abordagem fuzzy: F GRAU DE PERTINÊNCIA ao conjunto A: [0; 1]

Conjuntos Clássicos ou Crisp: definições • Definição de um conjunto crisp A: F lista de seus membros: A={a 1, a 2, . . , an} F propriedade P satisfeita pelos seus membros: A={x|P(x)} F função característica A , declara que elementos do conjunto universal X são membros de A: A (x) = 1 para x A 0 para x A Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Crisp: conceitos • Cardinalidade de A: |A| é igual ao número de elementos de um conjunto finito A • Complemento relativo de A em relação ao conjunto B: B-A={x| x B e x A} • Complemento absoluto de A em relação ao conjunto universal X: A Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Crisp: conceitos • União: A B={x| x A OU x B} • Intersecção: A B={x| x A E x B} Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Crisp: propriedades de operações • Involução: (Ac)c = A • *Comutatividade: A B = B A ; A B = B A • *Associatividade: (A B) C = A (B C) = (A B) C • Distributividade: A (B C) = (A B) (A C) Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Crisp: propriedades de operações • *Idempotência: A A = A ; A A = A • *Absorção: A (A B)=A ; A (A B)=A • Identidade: A =A ; A X=A Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Clássicos: lattice Um sistema A = ( , f 1, f 2, . . . , fn) onde o elemento é um conjunto e os outros elementos são operações definidas neste conjunto então A é denominada uma estrutura algébrica. • Uma estrutura algébrica é uma lattice se atende às seguintes propriedades: F Idempotência F Comutatividade F Associatividade F Absorção Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Crisp: leis • Lei da Contradição: A Ac = • Lei do Meio Excluído: A Ac = X • Leis de Morgan: Profa. Silvia Modesto Nassar silvia@inf. ufsc. br (A B)c = Ac Bc

Conjuntos Crisp: propriedades • Conjuntos disjuntos: • Partição: A 1 Profa. Silvia Modesto Nassar silvia@inf. ufsc. br A B = (A) = {Ai | i I , Ai A} Ai Aj= e Ai =A A 2 A 3 A 4 A

Conjuntos Difusos (Fuzzy): função de pertinência • Seja A um conjunto fuzzy e X um conjunto universal crisp então a função de pertinência dos elementos de X ao conjunto A é denotada por: A : X [0; 1] F números difusos F variáveis difusas Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

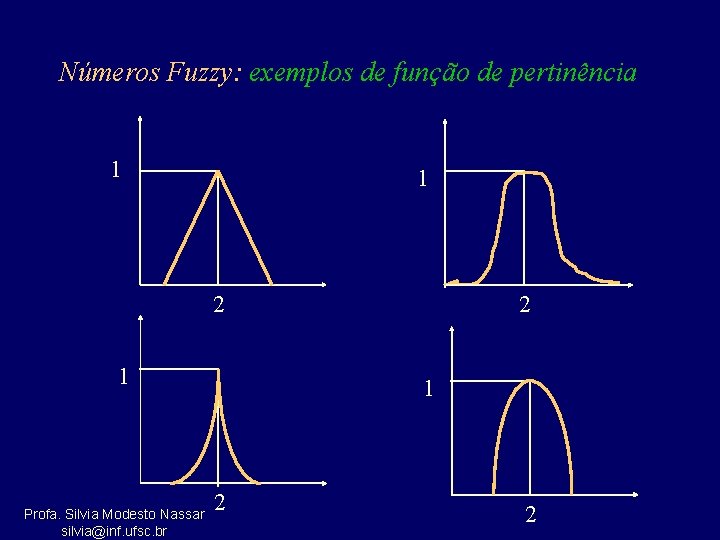
Números Fuzzy: exemplos de função de pertinência 1 1 2 1 Profa. Silvia Modesto Nassar silvia@inf. ufsc. br 2 1 2 2

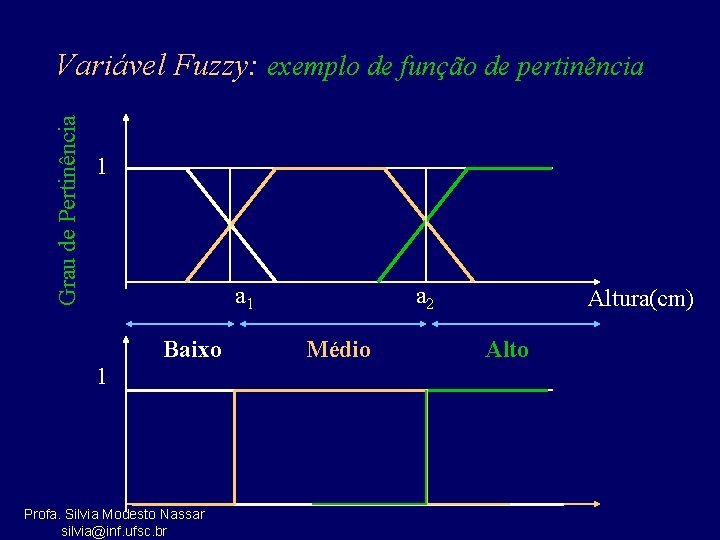
Grau de Pertinência Variável Fuzzy: exemplo de função de pertinência 1 Baixo 1 Profa. Silvia Modesto Nassar silvia@inf. ufsc. br a 2 Médio Altura(cm) Alto

Conjuntos Difusos: notação • Seja A um conjunto difuso e ai o grau de pertinência do elemento xi de X ao conjunto A • Sejam xi’s os elementos suporte de A • Notação: A = a 1/x 1 + a 2/x 2 +. . . + an/xn A = ai/xi Profa. Silvia Modesto Nassar silvia@inf. ufsc. br ou A = A(x)/x x

Conjuntos Difusos: conceitos básicos • • - cut suporte core ou núcleo altura: F normal F subnormal • conjunto difuso convexo Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Difusos: conceitos básicos • - cut e strong - cut : Dado um conjunto fuzzy A definido em X e um número [0; 1] um conjunto - cut é um conjunto crisp definido por A = { x| A(x) } + Profa. Silvia Modesto Nassar silvia@inf. ufsc. br A = { x| A(x) } strong - cut

Conjuntos Difusos: propriedades -cut e strong -cut Dado um conjunto fuzzy A definido em X e o par 1 e 2 [0; 1] tal que 1 2 então: F 1 A 2 A e 1+ A 2+ A F ( 1 A 2 A) = 2 A e ( 1+ A 2+ A) = 2+ A F ( 1 A 2 A) = 1 A e ( 1+ A 2+ A) = 1+ A Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

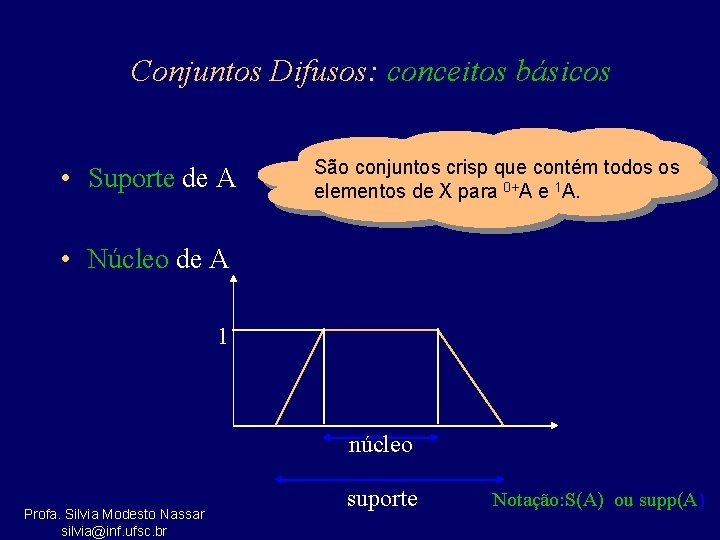
Conjuntos Difusos: conceitos básicos • Suporte de A São conjuntos crisp que contém todos os elementos de X para 0+A e 1 A. • Núcleo de A 1 núcleo Profa. Silvia Modesto Nassar silvia@inf. ufsc. br suporte Notação: S(A) ou supp(A)

Conjuntos Difusos: conceitos básicos h(A) F normal: se h(A) = 1 F subnormal: se h(A) 1 Profa. Silvia Modesto Nassar silvia@inf. ufsc. br height • Altura de A:

Conjuntos Difusos: operações padrão • Cardinalidade escalar: | A | |A| = A(x) x X F “sigma count” Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Difusos: operações padrão • Complemento: A(x) = 1 - A(x) F pontos de equilíbrio: são os elementos de X onde Profa. Silvia Modesto Nassar silvia@inf. ufsc. br A (x) = A(x)

Conjuntos Difusos: operações-padrão Sejam dois conjuntos difusos A e B: • União : t-conormas ( A B ) x = max[ A(x), B(x)] • Intersecção: t-normas ( A B ) x = min[ A(x), B(x)] Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Convexidade: conjunto crisp • Seja A um conjunto em Rn. q A é um conjunto convexo IFF F para todos os pares de pontos r e s de A F para todo numero real [0; 1] M o ponto t definido por t = r + (1 - ) s também está em A Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

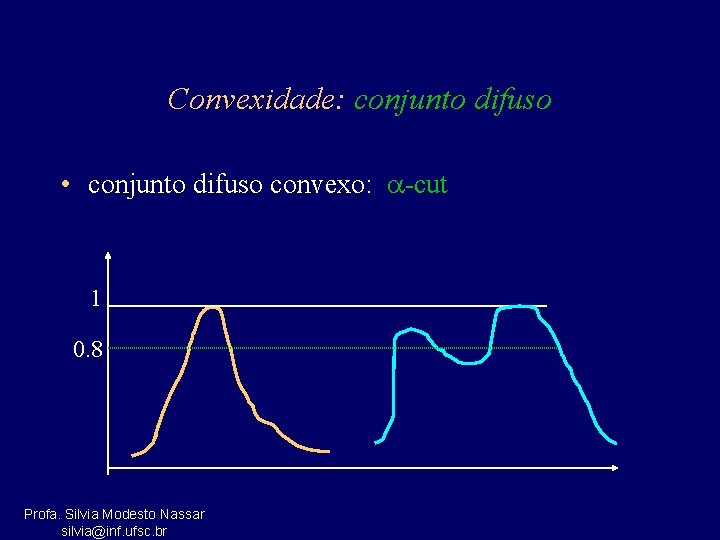
Convexidade: conjunto difuso • conjunto difuso convexo: -cut 1 0. 8 Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

Conjuntos Difusos: tipos • Ordinário: grau de pertinência F a cada elemento de X pode ser associado um particular número real F pode ser especificada uma função de pertinência A: X [0; 1] • Intervalo-valorado: intervalo de grau de pertinência A: X [0; 1] Profa. Silvia Modesto Nassar silvia@inf. ufsc. br

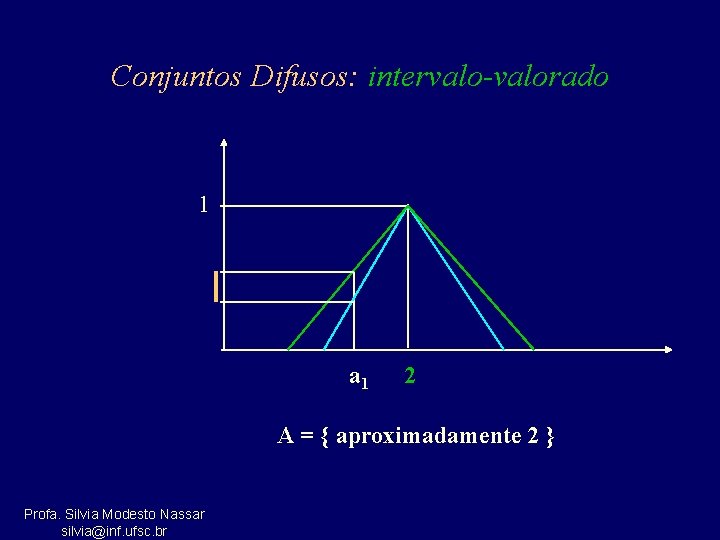
Conjuntos Difusos: intervalo-valorado 1 a 1 2 A = { aproximadamente 2 } Profa. Silvia Modesto Nassar silvia@inf. ufsc. br