RAZONAMIENTO APROXIMADO Sistemas Difusos Fuzzy Systems Introduccin a

RAZONAMIENTO APROXIMADO Sistemas Difusos (Fuzzy Systems) Introducción a la Inteligencia Artificial LCC 1

RAZONAMIENTO APROXIMADO (RA) Trata como REPRESENTAR COMBINAR y REALIZAR INFERENCIAS conocimiento impreciso y/o incierto 2

RA: Distintos modelos MODELOS PROBABILISTICOS MODELO EVIDENCIAL MODELO POSIBILISTICO § Todos tratan la incertidumbre en un sistema de producción § Sólo el modelo posibilístico puede tratar la imprecisión. 3

RA: Distintos modelos Ø MODELO POSIBILISTICO § Como representar, combinar y realizar inferencias conocimiento impreciso 4

CONOCIMIENTO IMPRECISO El conocimiento cuenta con predicados o cuantificadores vagos (no precisos) Ejemplos: • Pedro tiene entre 20 y 25 años. • Juan es joven • Mucha gente juega al fútbol • El espectáculo es para gente grande. 5

Lógica difusa Introducción Teoría de conjuntos difusos Teoría de conjuntos clásica (conjuntos nítidos) • Conjuntos Difusos • – – • Operaciones elementales conjuntos difusos – – – Funciones de pertenencia Etiquetas lingüísticas Complemento Intersección Unión Razonamiento difuso Inferencia difusa • Decodificación • Funcionamiento de un sistema difuso Conclusiones 6

Necesidad de razonamiento difuso En el mundo real existe mucho conocimiento con las siguientes características: conocimiento vago, impreciso, incierto, ambiguo, inexacto, o probabilístico por naturaleza. El razonamiento y pensamiento humano frecuen-temente conlleva información de este tipo: • imprecisión inherente de los conceptos humanos y • razonamiento basado en experiencias similares, pero no idéntica Problema: Poca capacidad de expresión de la lógica clásica. § Ejemplo 1. Clasificación de personas en altas o bajas § Ejemplo 2. Definición del término joven 7

Going Fuzzy … Examples of Fuzzy statements: § § The motor is running very hot. Tom is a very tall guy. Electric cars are not very fast. High-performance drives require very rapid dynamics and precise regulation. § Leuven is quite a short distance from Brussels. § Leuven is a beautiful city. § The maximum range of an electronic vehicle is short. If short means: 300 km or less, would 301 km be long ? § Want to express to what degree a property holds. 8

Fuzzy sets: Are functions: f: domain [0, 1] Crisp set (tall men): 1 0 150 160 170 180 190 200 210 cm Fuzzy set (tall men): 1 0 150 160 170 9

Representing a domain: Crisp sets (men’s height): 1 short 0 150 160 tall medium 170 180 190 200 210 cm Fuzzy set (men’s height): 1 short 0 150 160 medium 170 180 tall 190 10

Razonamiento inexacto Es necesario cuantificar y razonar acerca de términos o predicados difusos que aparecen en el lenguaje natural. La lógica difusa se refiere a estos términos como variables lingüísticas, y la tecnología de los sistemas expertos, incorpora estas variables lingüísticas en reglas que pasan a ser reglas difusas. 11

Lógica difusa En 1965, Lofti Zadeh sienta las bases de la lógica difusa § Motivación inicial: estudio de la vaguedad Relación vaguedad incertidumbre § Solución: definir conjuntos con grados de pertenencia § Éxito de la lógica difusa : Desde el punto de vista práctico: miles de aplicaciones, la mayoría en sistemas de control • Desde el punto de vista lógico: lógica fuzzy como una lógica multivaluada. • 12

Características principales de la lógica difusa Se intenta representar la vaguedad e imprecisión inherentes en el lenguaje natural u Utiliza varios elementos: conjuntos difusos, variables difusas, relaciones difusas, reglas difusas (lenguaje difuso) u Dichos elementos se combinan entre sí en el proceso de inferencias (fuzzy logic) u Fuzzy control: El proceso de inferencias incluye pasos que pasan la información precisa a difusa y viceversa u 13

Lógica difusa Por definición “logica difusa” es una rama de la lógica que utiliza grados de pertenencia a los conjuntos (grados de verdad de las fórmulas) en lugar de los estrictos valores verdadero o falso. Estos conjuntos reciben la denominación de “conjuntos difusos”. 14

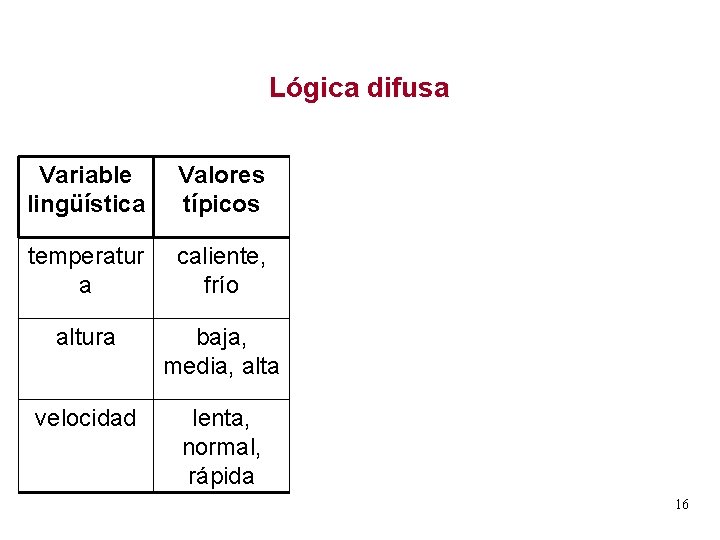
Lógica difusa La lógica difusa concierne a la cuantificación y razonamiento sobre términos vagos o difusos que aparecen en el lenguaje natural cotidiano. En la lógica difusa, estos términos son denominados variables lingüísticas: son términos que describen algún concepto que usualmente tiene asociados valores vagos o difusos. 15

Lógica difusa Variable lingüística Valores típicos temperatur a caliente, frío altura baja, media, alta velocidad lenta, normal, rápida 16

Difusión de fuzzy logic • En la actualidad es un campo de investigación muy importante, tanto por sus implicaciones matemáticas o teóricas como por sus aplicaciones prácticas: § Revistas (Fuzzy Sets and Systems, IEEE Transactions on Fuzzy Systems. . ) § Congresos (FUZZ-IEEE, IPMU, EUSFLAT, ESTYLF. . . ) § Miles de aplicaciones reales: Control de sistemas: Tráfico, vehículos, compuertas en plantas hidroeléctricas, centrales térmicas, lavadoras, metros ascensores. . . • Predicción y optimización: Predicción de terremotos, optimización de horarios. . . • Reconocimiento de patrones y Visión por ordenador: Seguimiento de objetos con cámara, reconocimiento de escritura, reconocimiento de objetos, compensación de vibraciones en cámaras, sistemas de enfoque automático. . . • Sistemas de información o conocimiento: Bases de datos, sistemas expertos. . . • 17

Un poco de publicidad. . . OLYMPUS ERGONÓMICA SRL 28 -120 Poderoso lente zoom de 4. 3 x, 28 -120 con elementos de lentes de cristal ED Sistema de flash doble incorporado. Ajuste de Exposición Automática programada Sistema de Medición TTL: Fuzzy logic ESP, Promedio Balanceado al Centro AEG Lavamat 64600 Carga: 5 kg Revoluciones: 1400 rpm Características energéticas: A+, A, B Multi-Display Fuzzy Logic Programas especiales: Lavado a mano, Seda, Lana 18

Conjuntos difusos Conjuntos clásicos (crisp) § A U definido por su función de pertenencia § A: U {0, 1} / A(x)= 1 sii x A Conjunto difuso (Fuzzy set) A de U § A: U [0, 1] § A(x) me define el grado de pertenencia de x a A § Hay “distintos grados de pertenencia” 19

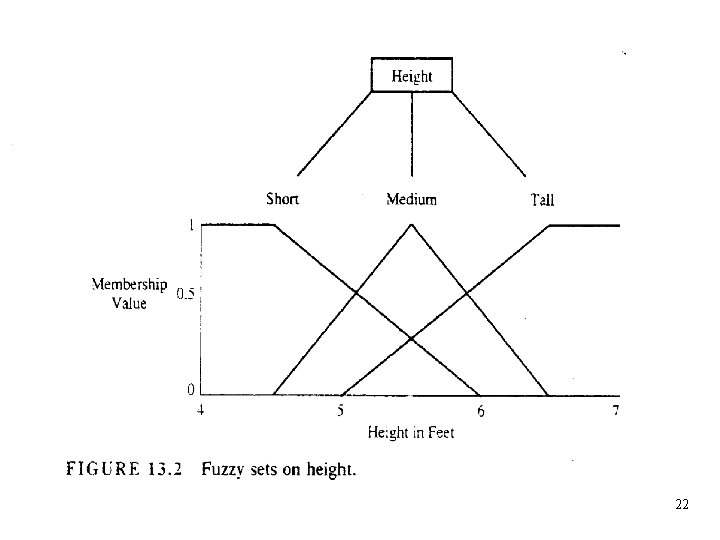
Conjuntos difusos La sentencia “Juan es alto” implica la variable “estatura” que tiene como valor lingüístico “alto”. El rango de los posibles valores de la variable lingüística (estatura) es el universo de discurso X de dicha variable [0. 3, 2. 5 m]. La frase “Juan es alto” restringe los valores de la variable estatura y se puede representar mediante un conjunto difuso. 20

Conjuntos difusos Para otras descripciones de la variable lingüística estatura tales como: baja o media, se pueden obtener otros conjuntos difusos que reflejan la opinión popular (o de expertos). se pueden definir múltiples conjuntos difusos para un mismo universo de discurso: subconjuntos difusos representando distintos términos vagos. 21

22

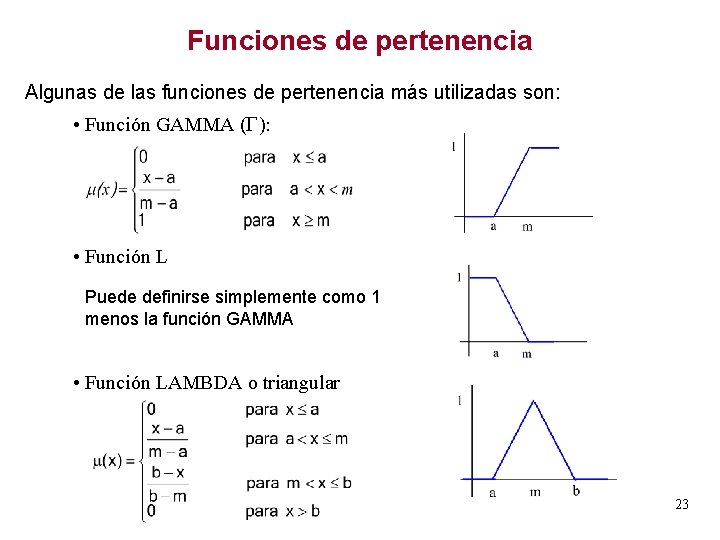
Funciones de pertenencia Algunas de las funciones de pertenencia más utilizadas son: • Función GAMMA ( ): • Función L Puede definirse simplemente como 1 menos la función GAMMA • Función LAMBDA o triangular 23

Funciones de pertenencia • Función PI o trapezoidal 24

Funciones de pertenencia • Función S • Función Z (opuesta de la S) Z(x) = 1 - S(x) • Función P 25

Conjunto difuso - espacio discreto Considerando ahora un universo de discurso discreto, tal que los elementos de X sean { x 1, x 2, . . . xn} y, siendo A un conjunto difuso definido en dicho universo: La representación del vector se clarifica utilizando el símbolo “ / “ que asocia el valor de pertenencia ai con la coordenada de xi : A = ( a 1 / x 1, a 2/x 2. . . an/ xn ) Considerando el conjunto difuso alto ALTO = (0/1. 65, 1/1. 75, 1/1. 85, 0/1. 95) 26

Conjunto difuso - espacio discreto También se expresa como: A = ( a 1 /x 1+ a 2/x 2+. . . +an/ xn ) A = i=, 1, n A(xi)/xi Si X es una función continua, el conjunto A, este puede ser representado como: A = A(xi)/xi 27

Etiquetas lingüísticas - Hedges Equivalentes a los adverbios del lenguaje natural Se utilizan para definir conjuntos difusos a partir de otros ya existentes. Por ejemplo, viejo —> MUY viejo Lo que se hace es componer la función de pertenencia con alguna otra función, de forma que la función resultante tenga la forma deseada Por ejemplo, función para el adverbio MUY —> f(y) = y 2 viejo Muy viejo 28

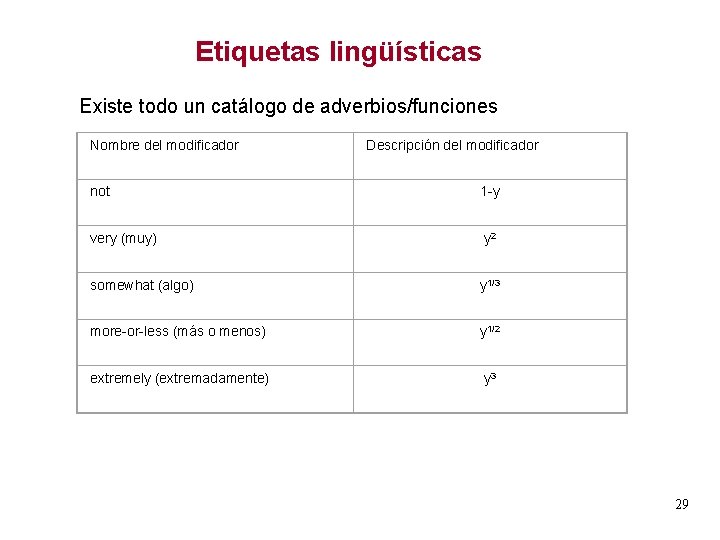
Etiquetas lingüísticas Existe todo un catálogo de adverbios/funciones Nombre del modificador Descripción del modificador not 1 -y very (muy) y 2 somewhat (algo) y 1/3 more-or-less (más o menos) y 1/2 extremely (extremadamente) y 3 29

Etiquetas lingüísticas Otras operaciones usuales Normalización f(y) = y/Altura Concentración f(y)=yp, con p>1 Dilatación f(y)=yp, con 0<p<1 Intensificación contraste Difuminación 30

Operaciones conjuntos difusos Complemento (Negación) Dado un conjunto difuso A, su complemento vendrá definido por Las funciones c para el complemento más utilizadas son: • c(a) = 1 - a. • Yager cw(a) = ( 1 - aw)1/w w [0, ] • Sugeno cl(a) = (1 -a)/(1 -la) l [0, 1] 31

Operaciones conjuntos difusos Intersección (conjunción) Dados conjuntos difusos A y B, su intersección vendrá definida por Las funciones i que verifican las propiedades que se esperan de una conjunción se llaman normas triangulares (t-normas). 32

Operaciones conjuntos difusos Algunas t-normas usuales: • t-norma del mínimo imin(a, b) = min(a, b) • t-norma del producto i*(a, b) = ab • t-norma del producto drástico 33

Operaciones conjuntos difusos Unión (disjunción) Dados conjuntos difusos A y B, su unión vendrá definida por Au. B(x) = u( A(x), B(x)) Las funciones u que verifican las propiedades esperadas para una disjunción se llaman: conormas triangulares (t-conormas). 34

Operaciones conjuntos difusos Si consideramos como complemento la función c(u) = 1 -u, las tconormas correspondientes a las t-normas anteriores son: • t-conorma del máximo umax(a, b) = max(a, b) • t-conorma de la suma u*(a, b) = a+b-ab • t-norma de la suma drástica 35

Operaciones conjuntos difusos Considerando la t-norma del mínimo (intersección, AND) junto con la t-conorma del máximo (unión, OR) Conjuntos vacío y total: § Conjunto vacío § Conjunto total (X crisp) Sin embargo, con esta definición no se satisfacen algunos famosos principios de la lógica clásica, como por ejemplo: Principio de contradicción Principio del tercero excluso 36

Razonamiento difuso Proposición difusa simple: § Proposición que asigna un valor a una variable difusa: “Pepe es de estatura mediana”. § Tiene asociado un conjunto difuso (función de pertenencia). Proposición difusa compuesta: § Agrupación de dos o más proposiciones difusas simples “la velocidad es normal” AND “el objeto está cerca” “la velocidad es alta” OR “el objeto está muy cerca” “la velocidad NO es alta” Necesidad de definir operadores difusos: § NO (¬p) ¬A(u) = 1 - A(u) § AND (p q) vendrá definida por una función de pertenencia tipo tnorma, por ejemplo A B (u, v) = min( A(u), B(v)) § OR (p q) vendrá definida por una función de pertenencia tipo tconorma, por ejemplo AUB(u, v) = max( A(u), B(v)) 37

Razonamiento difuso: implicaciones El siguiente paso es definir lo que es una implicación, es decir, asignar una función de pertenencia a una agrupación antecedente consecuente del tipo p q Esto nos permitirá razonar con afirmaciones tales como: SI “la velocidad es normal” ENTONCES “la fuerza de frenado debe ser moderada” Opciones: § Teórica: Dar a la implicación el mismo significado que en la lógica clásica. p q p q(u, v) = max(1 - A(u), B(v)) p q ~(p (~q)) p q(u, v) = 1 – min[ A(u), 1 - B(v)] § Práctica: Dar a la implicación el significado de relación causaefecto: Implicación de Mamdani p q A B p q(u, v) = min( A(u), B(v)) 38

Inferencia Difusa – Fuzzy inference Una regla difusa relaciona dos proposiciones difusas, por ejemplo considerando dos conjuntos difusos tales como A (estatura es alta) y B (peso es elevado), estos pueden estar relacionados por la regla: If A Then B Los sistemas expertos difusos almacenan las reglas como asociaciones difusas (A, B), en una matriz M denominada matriz asociativa difusa. 39

Matriz asociativa difusa. 40

Inferencia Difusa – Fuzzy inference Como en otras técnicas de razonamiento inexacto, el proceso de inferencia difusa intenta establecer la credibilidad conclusión de la regla dada una cierta evidencia en la premisa. If A Then B A* B* ? ? ? 41

Funcionamiento de un sistema de control basado en lógica difusa Entrada crisp Codificador Reglas Decodificador x Up Salida crisp y=f(x) V u Up Conjuntos difusos entrada Inferencia v V Conjuntos difusos salida 42

Inferencia Difusa – Fuzzy inference Disponiendo de la matriz M que se obtiene a partir de A B, el proceso de inferencia difusa permite a partir de información A’ (subconjunto de A), inducir un subconjunto B’ de B. Técnicas de inferencia difusas: § § Inferencia max-min Inferencia max-product 43

Inferencia max-min El operador de de la implicación utilizado es el “min”, min es decir: mij = min(ai, bj) Entonces, dados conjuntos difusas A y B, se obtiene la matriz M. Luego, dado el conuunto A’, se puede inducir el subconjunto B’. 44

Inferencia max-min Ejemplo: sea un universo de discurso X que representa “temperatura”, y A un conjunto difus que representa “temperatura normal”. Asumiendo que Y representa “velocidad” y un B que representa “velocidad media”, entonces si tenemos la siguiente regla difusa: If temperatura normal Then velocidad media IF A THEN B 45

Inferencia max-min - Ejemplo 46

A’ representa una entrada de t=125º 47

El subconjunto A’ (lectura única) induce un conjunto difuso B’ utilizando la composición max-min: 48

Inferencia max-min - Ejemplo 49

Inferencia max-min - Observación Cuando A’ tiene un solo valor de pertenencia distinto de 0, por ejemplo xk se puede utilizar solo A (xk) directamente con la representación de B, B (y) para inducir B’ como B’ = A (xk) B (y) Truncamiento del conjunto difuso B por el valor A(xk) 50

Inferencia max-min - Ejemplo En el ejemplo, nosotros asumimos que la temperatura es de 125 grados A’ tiene un solo valor de pertenencia distinto de 0, y resulta A (x) = 0. 5 Luego: B’ = [min(. 5, 0), min(. 5, . 6), min(. 5, 1), min(. 5, . 6), min(. 5, 0) = = (0, . 5, 0) 51

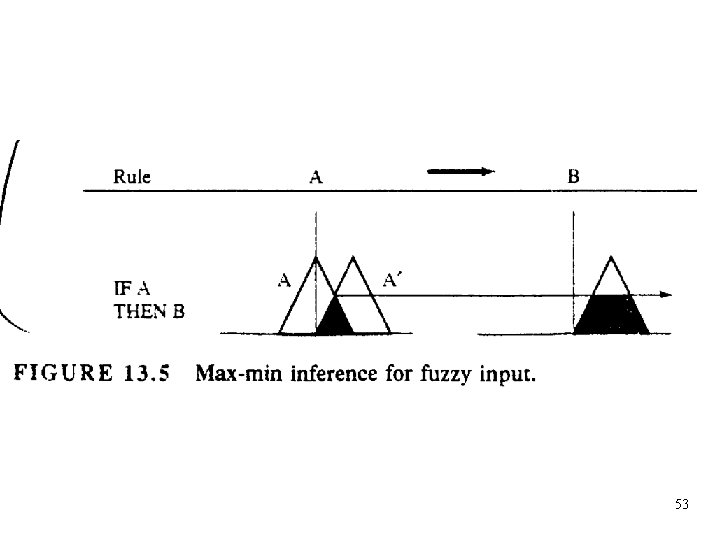
Inferencia max-min - Observación En el caso que la entrada a la regla sea una lectura difusa A’, nosotros podemos considerar la intersección de A y A’, es decir: min (ai, a’i) para inducir el B’ 52

53

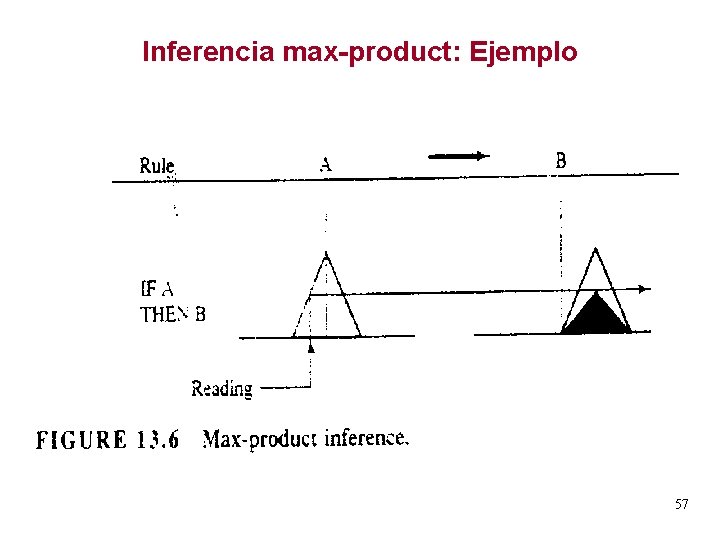
Inferencia max-product El operador de de la implicación utilizado es el producto en lugar del min: mij = ai * bj Dados los conjuntos difusos A y B, se obtiene la matriz M. Luego, dado el vector de ajuste de A’, se puede inducir el subconjunto B’. 54

Inferencia max-product: Ejemplo 55

Inferencia max-product : Ejemplo § A partir de la nueva matriz M se utiliza nuevamente la composición Max-min: 56

Inferencia max-product: Ejemplo 57

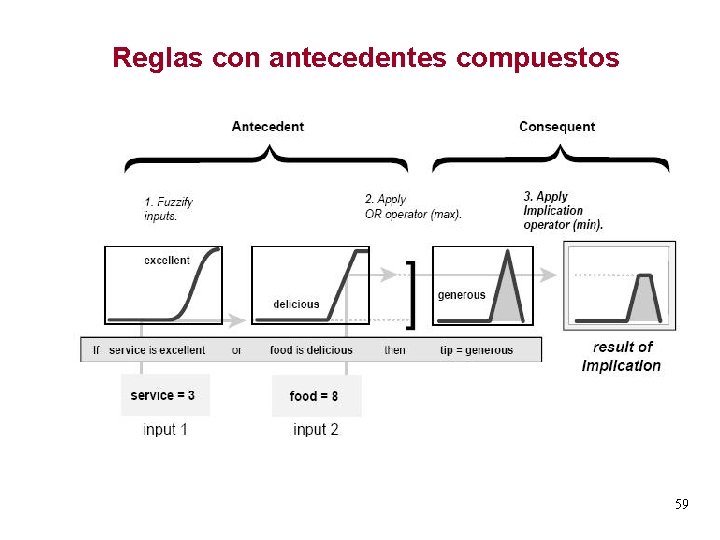
Inferencia Difusa El método numérico desarrollado puede ser extendido a reglas con cláusulas múltiples en la premisa vinculadas por operadores de conjunción o disyunción. Si A and/or B Entonces C La extensión del método consiste en incorporar las matrices asociativas a cada uno de los conjuntos difusos A y B involucrados en la regla y resolverlos conforme a la naturaleza del 58 operador que los vincula.

Reglas con antecedentes compuestos 59

Inferencia Difusa El efecto de la combinación de las conclusiones de varias reglas: R 1: A 1 C, . . . Rn: An C y el valor resultante del aporte de cada una de ellas, permite suponer que el resultado de la composición ( la unión): C’ = C’ 1 C’ 2 C’ 3. . . . C’n según las operaciones entre conjuntos difusos C’ = max (C’ 1 , C’ 2 , C’ 3 , . . . , C’n) 60

Decodificación - defuzzyfication Una vez llevado a cabo el proceso de razonamiento difuso, es necesario dotar al sistema de la capacidad de tomar decisiones. Así por ejemplo, el sistema debe saber qué fuerza de frenado que debemos aplicar si la velocidad es alta Para ello se utilizan las llamadas técnicas de decodificación, que transforman un conjunto difuso en un valor nítido. Las más usuales son: § El valor máximo (es decir, el más posible). § El centroide o centro de gravedad difuso 61

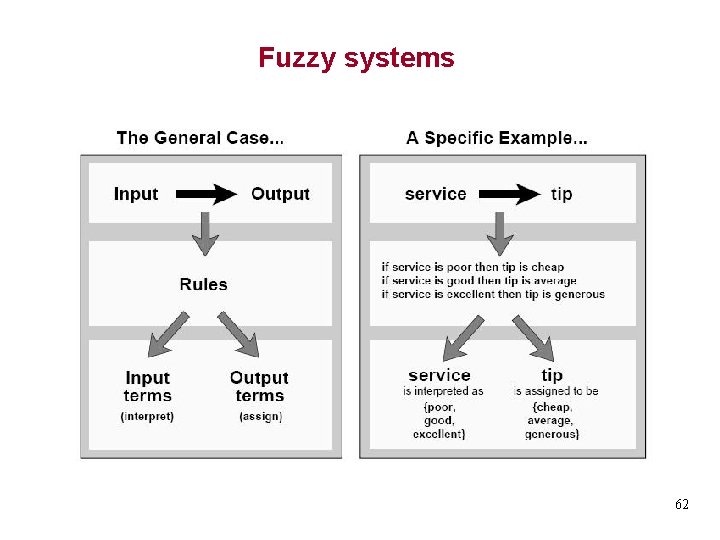
Fuzzy systems 62

Fuzzy systems 63

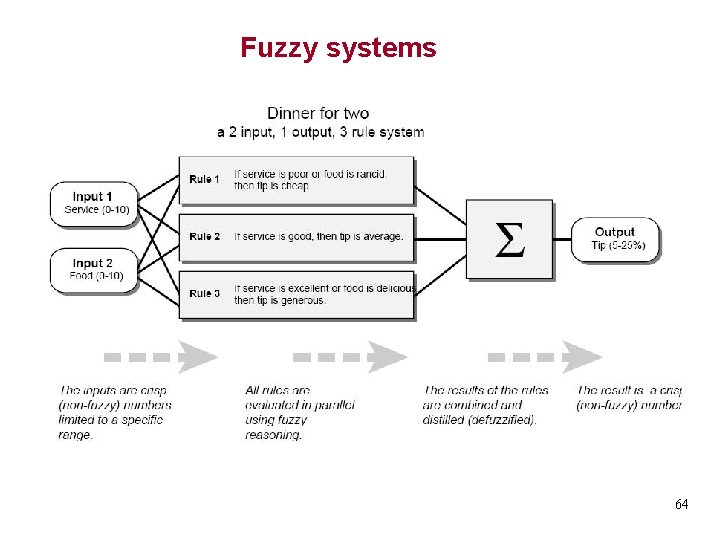
Fuzzy systems 64

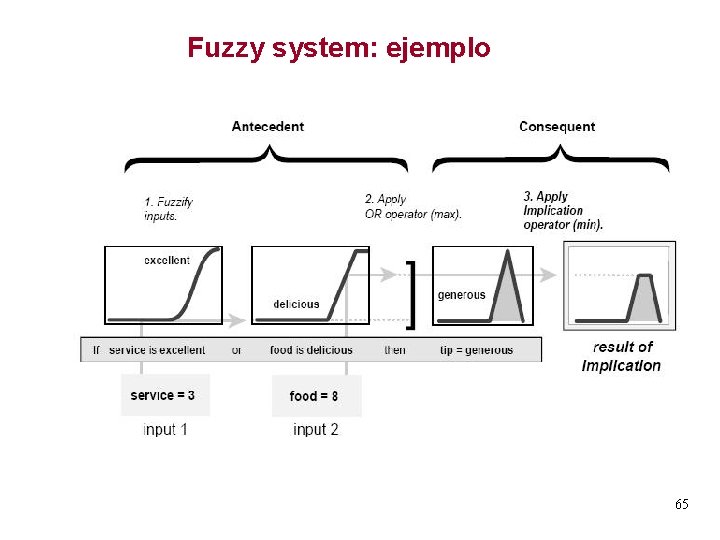
Fuzzy system: ejemplo 65

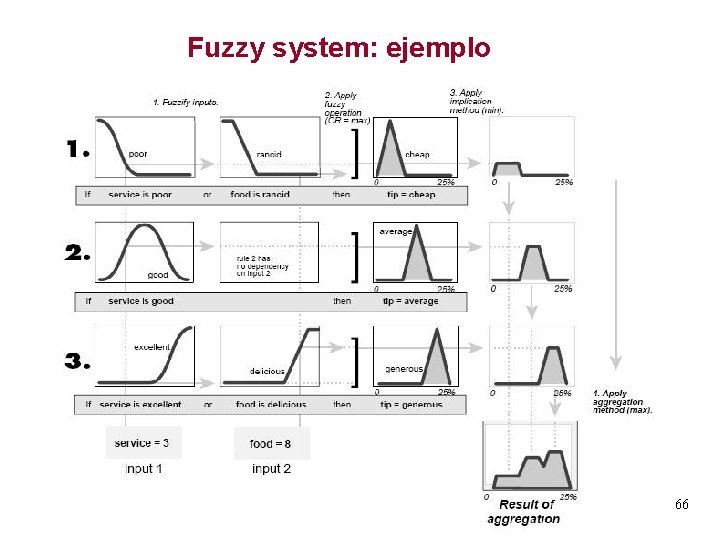
Fuzzy system: ejemplo 66

Fuzzy system: ejemplo 67

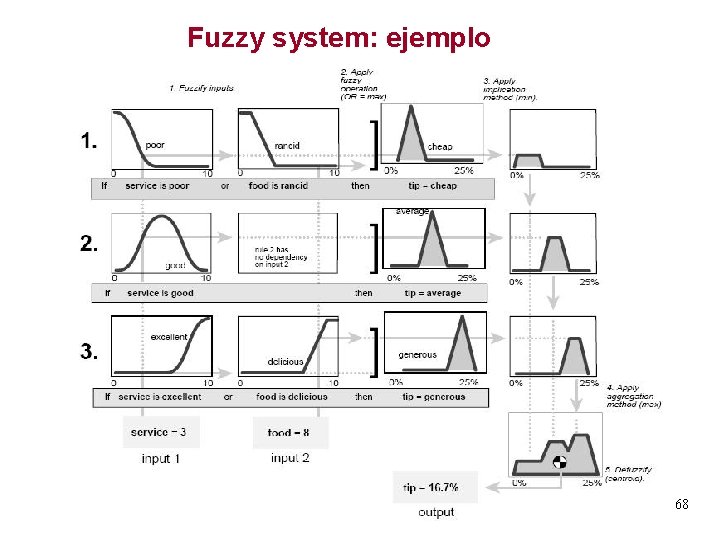
Fuzzy system: ejemplo 68

En resumen La lógica difusa se concibió originalmente como un método mejor para manejar y almacenar información imprecisa Ha demostrado ser una excelente alternativa para sistemas de control, ya que imita a la lógica de control humana Se pede incluir en cualquier sistema, desde dispositivos pequeños a sistemas de control complejos Usa un lenguaje impreciso pero muy descriptivo para operar con datos de entrada de una forma parecida a la usa un operador humano Es robusta y no demasiado dependiente de los datos de entrada y operadores elegido Incluso las primeras versiones funcionan bastante bien, con escasa necesidad de ajustes 69