conjuntouniverso conjunto A U conjunto complementar de A

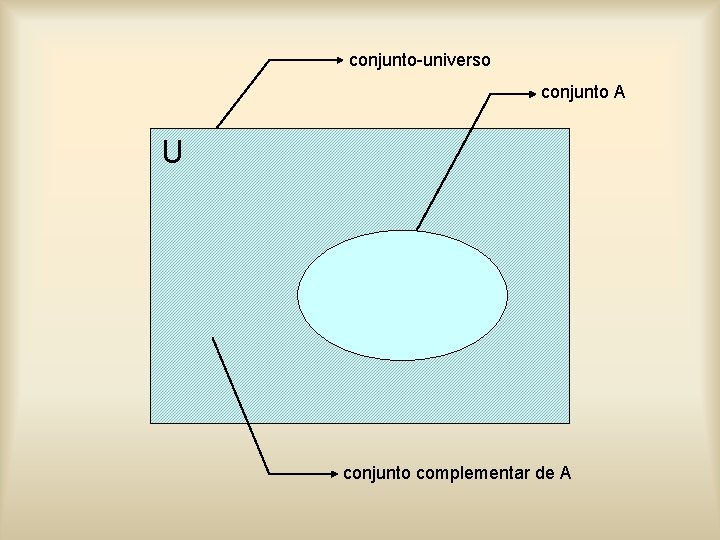
conjunto-universo conjunto A U conjunto complementar de A

Seja A U e x U. Temos que x A ou x A, não existindo uma terceira possibilidade. Princípio do Terceiro Excluído Uma proposição declarativa é verdadeira ou falsa, não ocorrendo um terceiro caso.

Seja A U e x U. Temos que x A ou x A, não sendo possível x A e x A simultaneamente. Princípio da Não-Contradição Uma proposição declarativa não pode ser verdadeira e falsa ao mesmo tempo.

QUANTIFICADORES para todo ou qualquer que seja existe | existe um único não existe A = {5, 6, 7, 8, 9} x A, x é maior do que 1. x A x é número primo. | x A; x é divisor de 10. x A; x é múltiplo de 10.

Observações: O símbolo “ ” é o conectivo condicional (se. . . , então. . . ), e o símbolo “ ” indica uma relação de implicação (. . . implica. . . ). O primeiro é um operador e o segundo uma relação. Semelhantemente, o símbolo “ ” é o conectivo bicondicional (. . . se, e somente se, . . . ), e o símbolo “ ” indica uma relação de equivalência (. . . equivale a. . . ). O primeiro é um operador e o segundo uma relação. Nesta apresentação, não distinguiremos “ ” de “ ”, e tampouco “ ” de “ ”.

IMPLICAÇÃO P Q P implica Q se P então Q P: x é retângulo. P Q: x é paralelogramo. Se x é retângulo então x é paralelogramo. A é o conjunto dos retângulos. A B B é o conjunto dos paralelogramos. A é subconjunto de B. P Q A B

EQUIVALÊNCIA P Q P equivale a Q P se, e somente se, Q P: x é triângulo equilátero. P Q: x é triângulo equiângulo. x é triângulo equilátero se, e somente se, x é triângulo equiângulo. A é o conjunto dos triângulos equiláteros. A=B B é o conjunto dos triângulos equiângulos. A é igual a B. P Q A=B

Tabelas-verdades p: eu estudo q: eu tiro boas notas p q V V F F F V V F F V P: conjunto das pessoas que estudam. Q: conjunto das pessoas que tiram boas notas. x = eu p q Q Q P P p q V V V P Q V F F Se x Q, então x P. F V F F F V P=Q Se x P, então x Q; e se x Q, então x P se, e somente se, x Q

É necessário ter 18 anos ou mais para possuir uma carteira de motorista? É suficiente? É suficiente quebrar a perna para sentir dor? É necessário? É necessário ser paralelogramo para ser retângulo? É suficiente ser retângulo para ser paralelogramo? É necessário? P condição suficiente Q condição necessária

É necessário ser triângulo equilátero para ser triângulo equiângulo? É suficiente? P condição necessária e suficiente Q condição necessária e suficiente

RECÍPROCA P: x 2 – 5 x + 6 = 0 Q: x {1, 2, 3} x 2 – 5 x + 6 = 0 x {1, 2, 3} P Q é verdadeira x {1, 2, 3} x 2 – 5 x + 6 = 0 Q P é falsa P Q e Q P são proposições recíprocas. Se uma proposição é verdadeira, não necessariamente sua recíproca também será. Mas podemos ter as duas verdadeiras. P: x 2 – 5 x + 6 = 0 R: x {2, 3} P R e R P são ambas verdadeiras.

Q: x é retângulo. P: x é paralelogramo. Q P Se ~Q é verdadeira, nada podemos concluir sobre P. Se P é verdadeira, nada podemos concluir sobre Q. Se ~P é verdadeira, necessariamente devemos ter ~Q verdadeira. U P Q Q P x Q x P Q = conjunto dos retângulos. P = conjunto dos paralelogramos. ( Q P) Se x Q não podemos dizer que x P ou que x P. Se x P não podemos dizer que x Q ou que x Q. Se x P então, necessariamente, x Q.

Q P equivale a ~P ~Q é a contrapositiva de Q P Q: x é retângulo P: x é paralelogramo Q P ~P ~Q Se x é retângulo, então x é paralelogramo. Se x não é paralelogramo, então x não é retângulo.

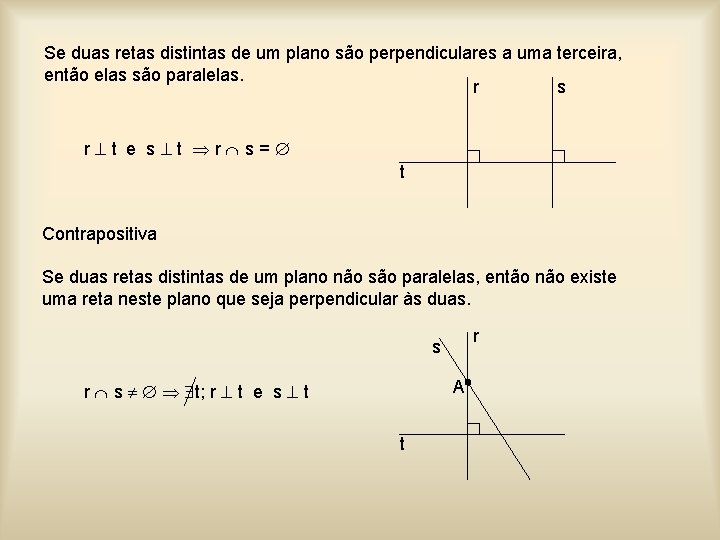
Se duas retas distintas de um plano são perpendiculares a uma terceira, então elas são paralelas. r s r t e s t r s= t Contrapositiva Se duas retas distintas de um plano não são paralelas, então não existe uma reta neste plano que seja perpendicular às duas. r s A r s t; r t e s t t

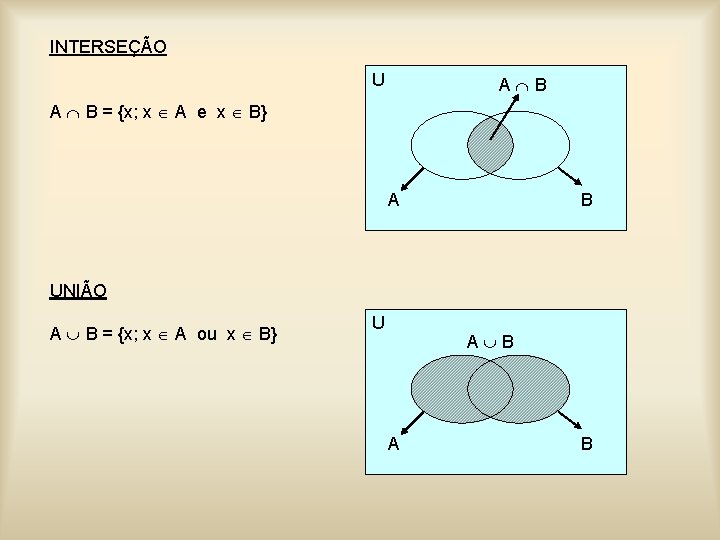
INTERSEÇÃO U A B A B = {x; x A e x B} A B UNIÃO A B = {x; x A ou x B} U A B

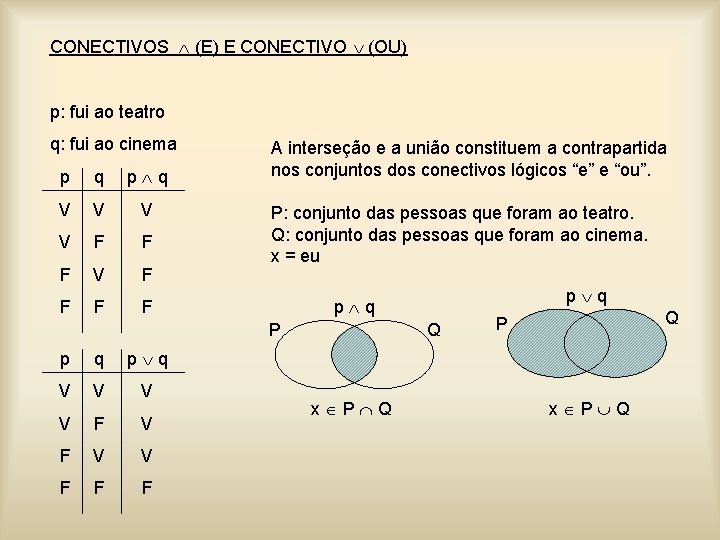
CONECTIVOS (E) E CONECTIVO (OU) p: fui ao teatro q: fui ao cinema p q V V F F F V F F A interseção e a união constituem a contrapartida nos conjuntos dos conectivos lógicos “e” e “ou”. P: conjunto das pessoas que foram ao teatro. Q: conjunto das pessoas que foram ao cinema. x = eu P p q V V F F F p q Q x P Q Q P x P Q

PROPRIEDADES COMUTATIVA A B=B A ASSOCIATIVA (A B) C = A (B C) DISTRIBUTIVA A (B C) = (A B) (A C)

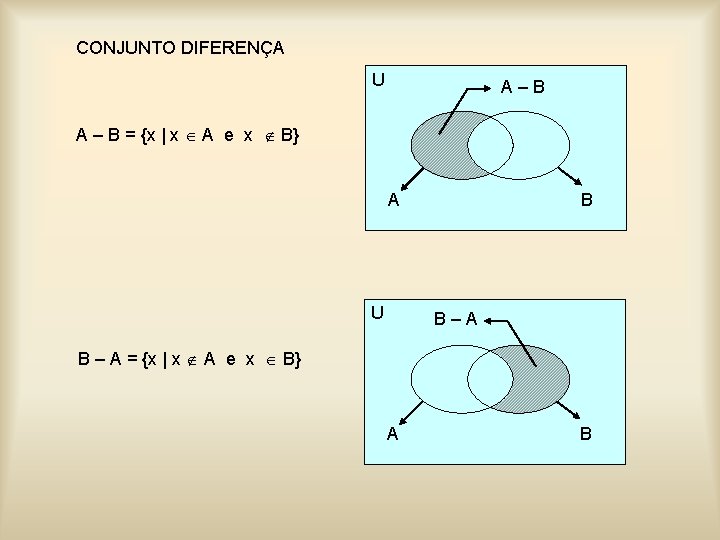
CONJUNTO DIFERENÇA U A–B A – B = {x | x A e x B} A U B B–A B – A = {x | x A e x B} A B

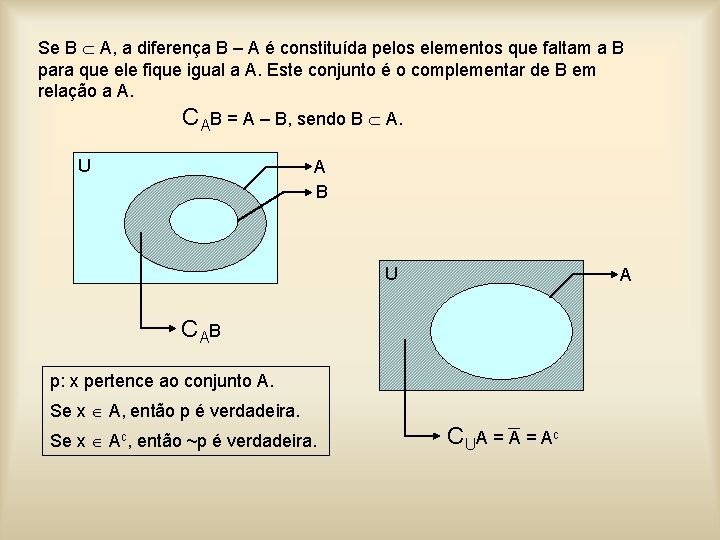
Se B A, a diferença B – A é constituída pelos elementos que faltam a B para que ele fique igual a A. Este conjunto é o complementar de B em relação a A. CAB = A – B, sendo B A. U A B U A CA B p: x pertence ao conjunto A. Se x A, então p é verdadeira. Se x Ac, então ~p é verdadeira. C UA = A c

Leis De Morgan Sejam A e B dois conjuntos no universo U. Consideremos o complementar da união de A com B, (A B)c. x (A B)c x (A B) x A e x B x Ac e x Bc x (Ac Bc) (A B)c e (Ac Bc) são formados pelos mesmos elementos. Logo, (A B)c = Ac Bc (O complementar da união é a interseção dos complementares. ) Consideremos, agora, o complementar da interseção de A e B, (A B)c. x (A B)c x (A B) x A ou x B x Ac ou x Bc x (Ac Bc) (A B)c e (Ac Bc) são formados pelos mesmos elementos. Logo, (A B)c = Ac Bc (O complementar da interseção é a união dos complementares. )

Leis De Morgan Sejam as proposições p: x A e q: x B p q ~p ~q p q ~(p q) ~p ~q V V F F V V F V F F V V ~(p q) (~p ~q) (A B)c = Ac Bc