Razonamiento Matemtico Inductivo vs deductivo Conjetura n Una

Razonamiento Matemático Inductivo vs. deductivo

Conjetura n Una conjetura es una suposición fundamentada en observaciones repetidas de un patrón o proceso particular.

Razonamiento Inductivo n El razonamiento inductivo se caracteriza por sacar una conclusión general (haciendo una conjetura) a partir de observaciones repetidas de ejemplos específicos. La conjetura puede ser verdadera o falsa.

Ejemplo: R. Inductivo n n n n 2, 9, 16, 23, 30. ¿Cual es el próximo número? 2+7=9 9 + 7 = 16 16 + 7 = 23 23 + 7 = 30 30 + 7 = 37 ? Usted razónó utilizando los números previos de la lista

Razonamiento Deductivo n El razonamiento deductivo se caracteriza por la aplicación de principios generales a ejemplos específicos. n El principio general puede resumirse en una formula o ley.

Ejemplo: R. deductivo n Usted quiere demostrar que el área de una sala rectangular es 300 pies cuadrados. n Usted mide la sala y determina que es 15 pies por 20 pies. n Luego utiliza la formula general para el área de un rectángulo Área = longitud x ancho n Área = 20 pies x 15 pies = 300 pies cuadrados n

Razonamiento: Argumento Lógico n Premisas: una suposición, una ley, una regla, una idea ampliamente aceptada, o una observación. n Razonamiento deductivo o inductivo utilizando las premisas n Conclusión

Ejemplo: R. inductivo Ejemplo: 2 premisas y 1 conclusión n Nuestra casa esta construida de ladrillo rojo. n Mis dos vecinos inmediatos tienen casas de ladrillo rojo. n Por lo tanto, todas las casas de nuestro vecindario están construidas de ladrillo rojo.

Ejemplo: R. deductivo Ejemplo: 2 premisas y 1 conclusión n Todos los procesadores de palabra puede imprimir la letra p n Yo tengo un procesador de palabras. n Yo puedo imprimir la letra p.

Patrones numéricos n 1 = 12 n 1 + 3 = 22 n 1 + 3 + 5 = 32 n 1 + 3 + 5 + 7 = 42 n 1 + 3 + 5 + 7 + 9 = 52 n Lado Izq. Números naturales impares. n Lado derecho es el cuadrado de los números del lado izquierdo. n 1 + 3 + 5 + …+ (2 n – 1) = n 2 n n es cualquier numero natural

Diagramas de Venn y subconjuntos

Conjunto n grupo de objetos n Los objetos pertenecientes al conjunto reciben el nombre de elementos o miembros del conjunto. n Los conjuntos se expresan de las tres maneras siguientes: Descripción verbal n Enumeración o listado n Notación de construcción de conjuntos n

Expresión de conjuntos n Descripción verbal n El conjunto de los números naturales pares menores que diez n Enumeración n {2, 4, 6, 8} n Notación de construcción de conjuntos n {x | x es un numero natural par menor que 10}

Diagramas de Venn n John Venn (1834 -1923) n Dibujos y Diagramas utilizados en la Teoría de conjuntos

Conjunto Universal U

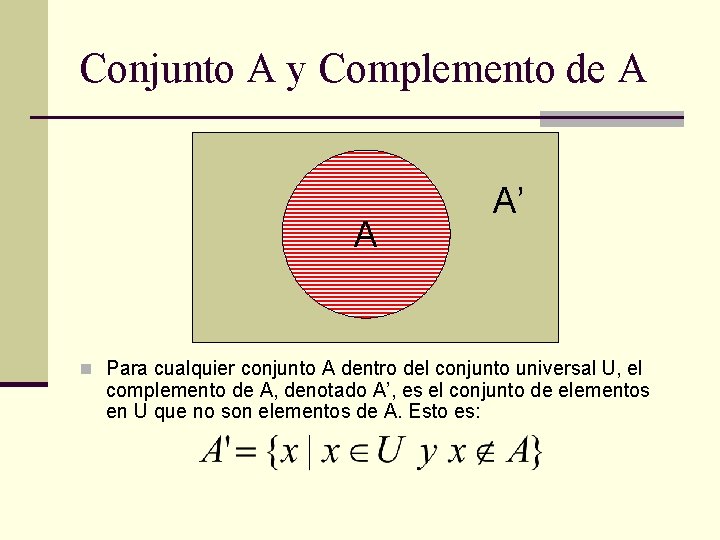
Conjunto A y Complemento de A A A’ n Para cualquier conjunto A dentro del conjunto universal U, el complemento de A, denotado A’, es el conjunto de elementos en U que no son elementos de A. Esto es:

Conjunto Vacío n El complemento del conjunto universal es el conjunto vacío n U’ = Ø n No tiene elementos n Es un subconjunto de todos los conjuntos

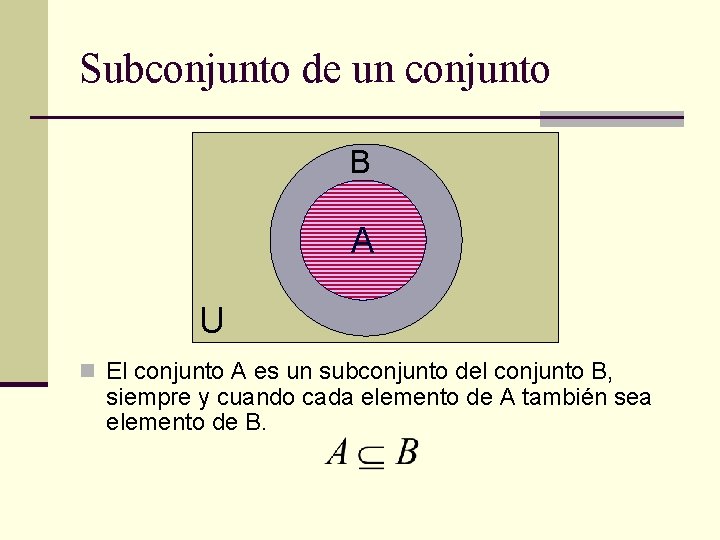
Subconjunto de un conjunto B A U n El conjunto A es un subconjunto del conjunto B, siempre y cuando cada elemento de A también sea elemento de B.

Cuantos subconjuntos hay en un conjunto n Cualquier conjunto (excepto Ø) tiene por lo menos dos subconjuntos, Ø y el mismo. n {7, 8} n Ø, {7}, {8}, {7, 8} n El numero de subconjuntos de un conjunto con n elementos es 2 n n El numero de subconjuntos propios de un conjunto es 2 n -1

Determinar el conjunto potencia n Dado el conjunto A ={5, 6} determina el conjunto potencia P(A) = { }. n El numero de subconjuntos del conjunto potencia es 2 n. Dado que A consta de 2 elementos, entonces 22 es 4 elementos n P(A) = {{5}, {6}, {5, 6}, Ø}

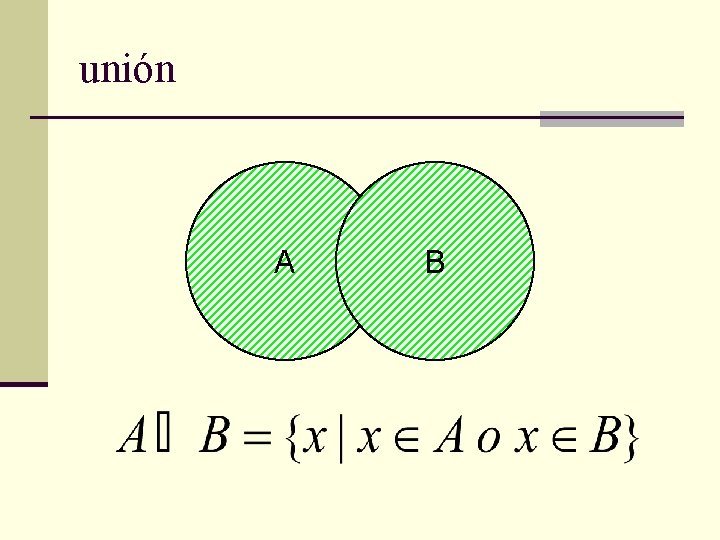
unión A B

Ejemplo de unión de conjuntos

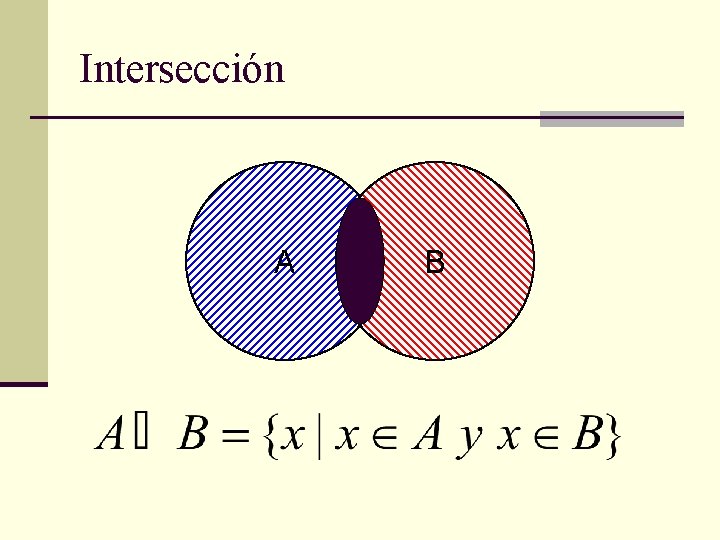
Intersección A B

Ejemplo de intersección de conjuntos

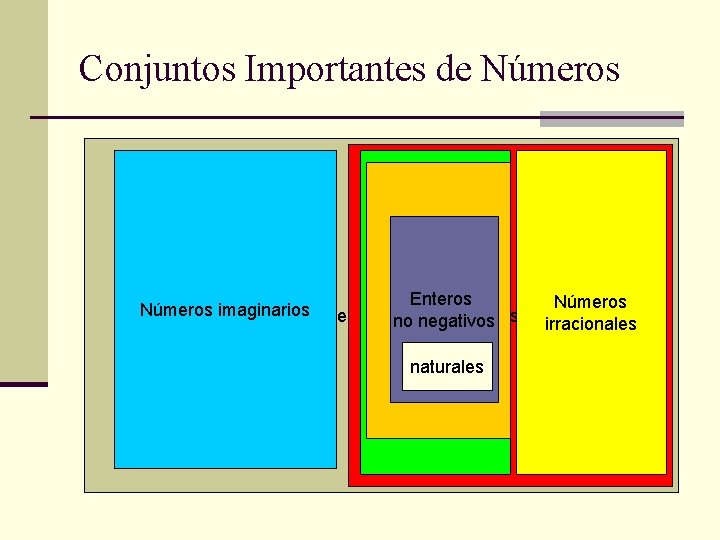
Conjuntos Importantes de Números Enteros Números imaginarios Números Complejos Números reales no negativos racionales irracionales naturales