INF 1366 Computao Grfica Interativa Cmeras e Transformaes

INF 1366 – Computação Gráfica Interativa Câmeras e Transformações Projetivas Alberto B. Raposo e Marcelo Gattass abraposo@tecgraf. puc-rio. br http: //www. tecgraf. puc-rio. br/~abraposo/INF 1366 Alberto Raposo – PUC-Rio

Cena em Computação Gráfica • 3 etapas – Especificação: • Modelagem geométrica, transformações básicas (rotação, translação, escalamento), etc. – Visualização • Qual porção da cena é vista – Renderização • Como visualizar Alberto Raposo – PUC-Rio

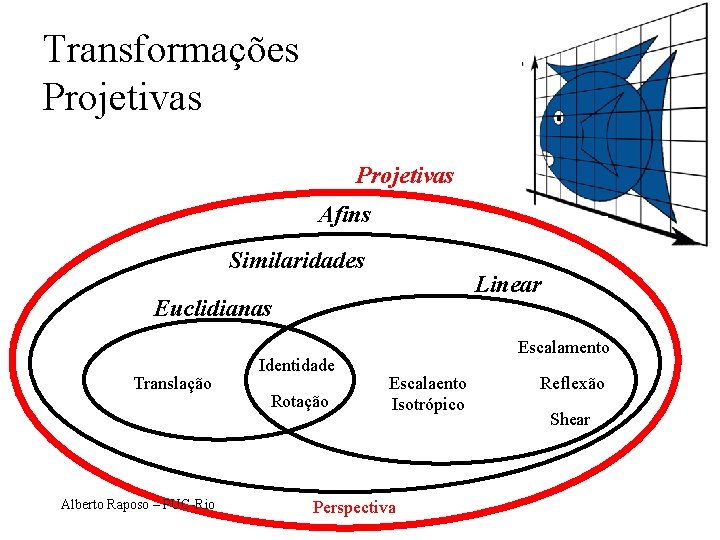
Transformações Projetivas Afins Similaridades Linear Euclidianas Translação Alberto Raposo – PUC-Rio Identidade Rotação Escalamento Escalaento Isotrópico Perspectiva Reflexão Shear

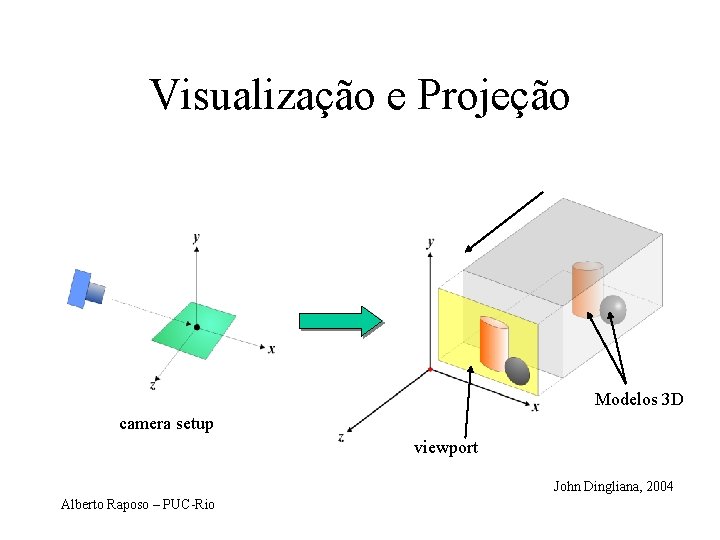
Visualização e Projeção Modelos 3 D camera setup viewport John Dingliana, 2004 Alberto Raposo – PUC-Rio

Projeção Representação de 3 dimensões em meios 2 D John Dingliana, 2004 Alberto Raposo – PUC-Rio

No início Alberto Raposo – PUC-Rio

Aprimoramentos. . . http: //www. stedwards. edu/hum/randle /s 32/SSgotpint/Frame. Set. htm http: //www. personal. us. es/jcordero/DISTANCIA/cap_09. htm Alberto Raposo – PUC-Rio

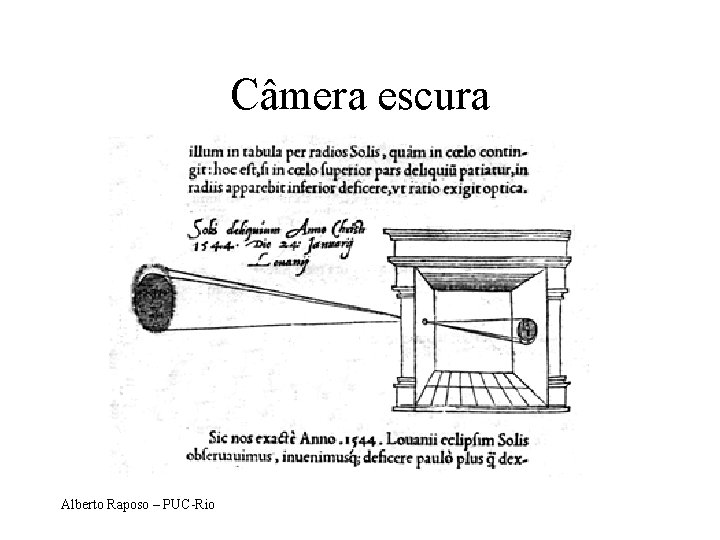
Câmera escura Alberto Raposo – PUC-Rio

Câmeras fotográficas Câmara escura - Leonardo da Vinci -1545 Alberto Raposo – PUC-Rio Luis-Jacques-Mandé Daguerre (1839)

Câmeras atuais Alberto Raposo – PUC-Rio

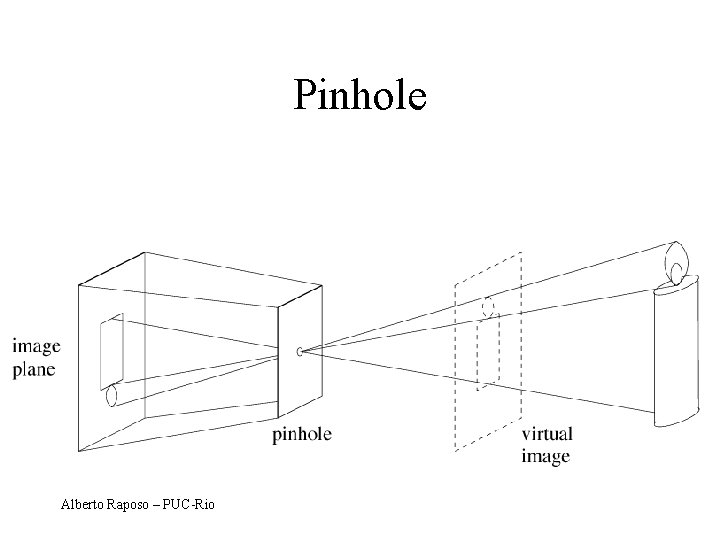
Pinhole Alberto Raposo – PUC-Rio

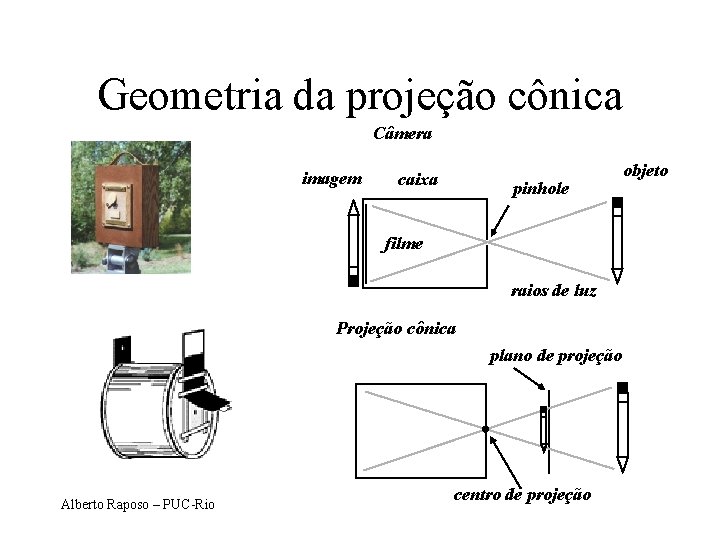
Geometria da projeção cônica Câmera imagem caixa pinhole filme raios de luz Projeção cônica plano de projeção Alberto Raposo – PUC-Rio centro de projeção objeto

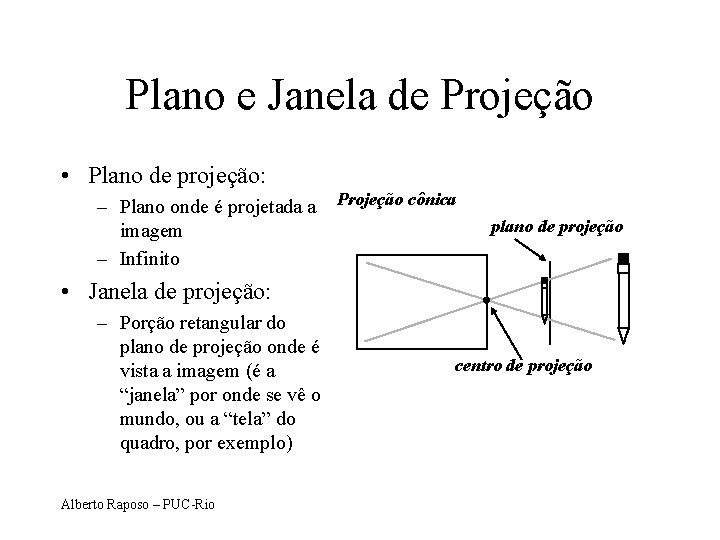
Plano e Janela de Projeção • Plano de projeção: – Plano onde é projetada a Projeção cônica imagem – Infinito plano de projeção • Janela de projeção: – Porção retangular do plano de projeção onde é vista a imagem (é a “janela” por onde se vê o mundo, ou a “tela” do quadro, por exemplo) Alberto Raposo – PUC-Rio centro de projeção

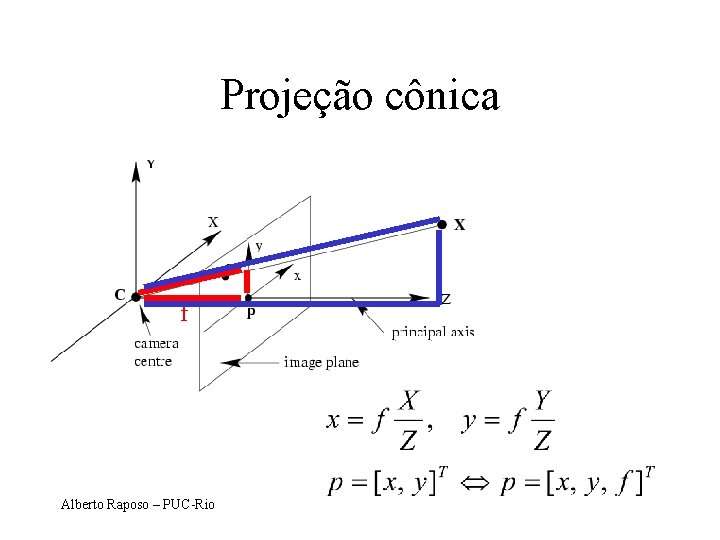
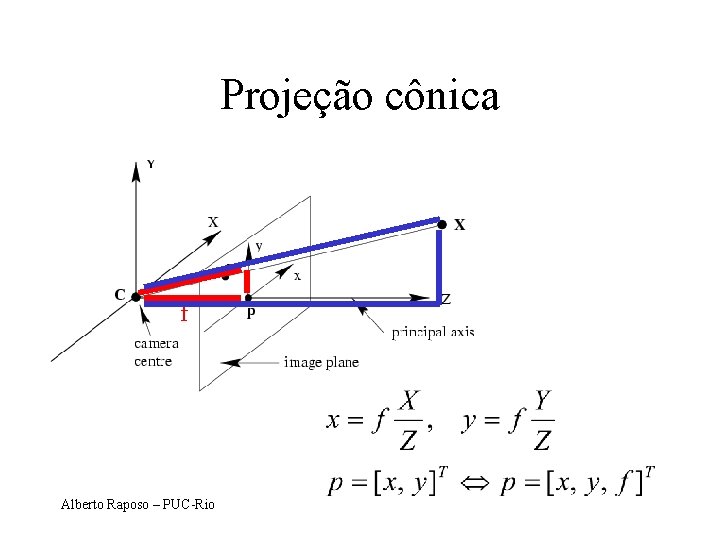
Projeção cônica f Alberto Raposo – PUC-Rio

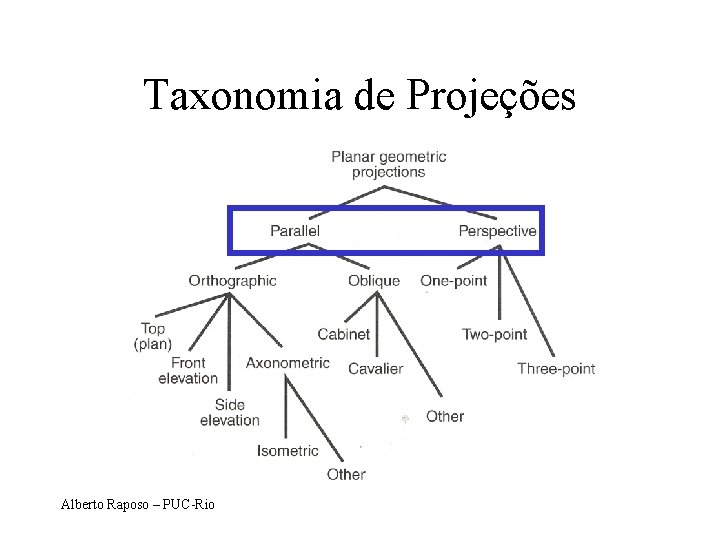
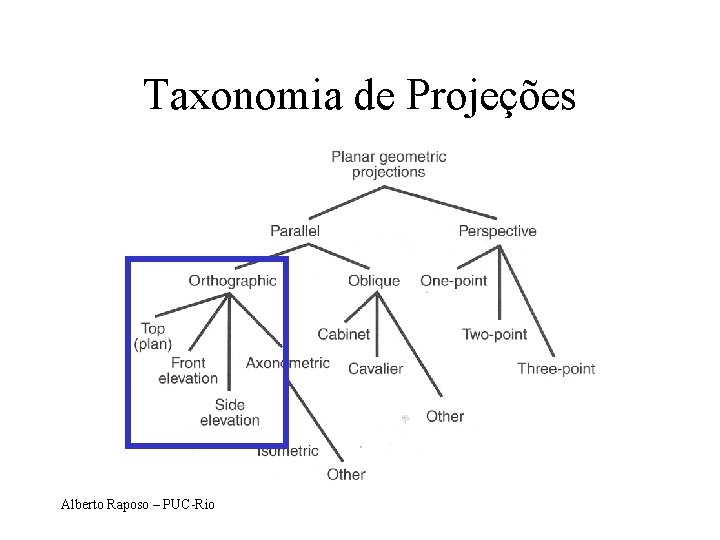
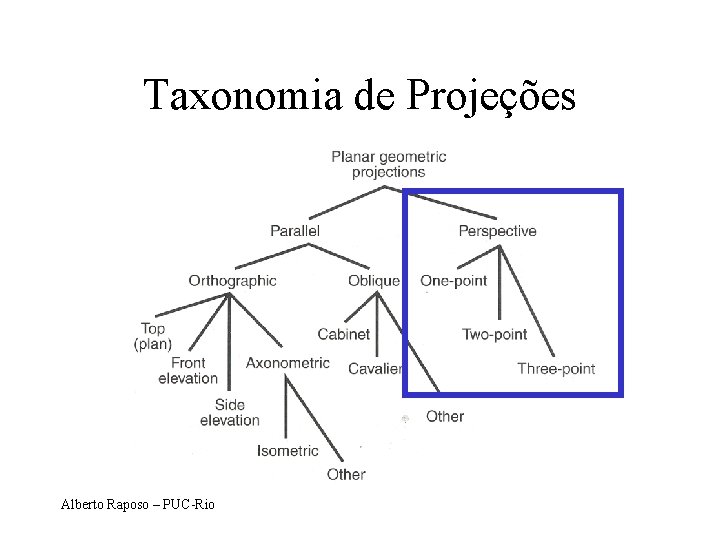
Taxonomia de Projeções Alberto Raposo – PUC-Rio

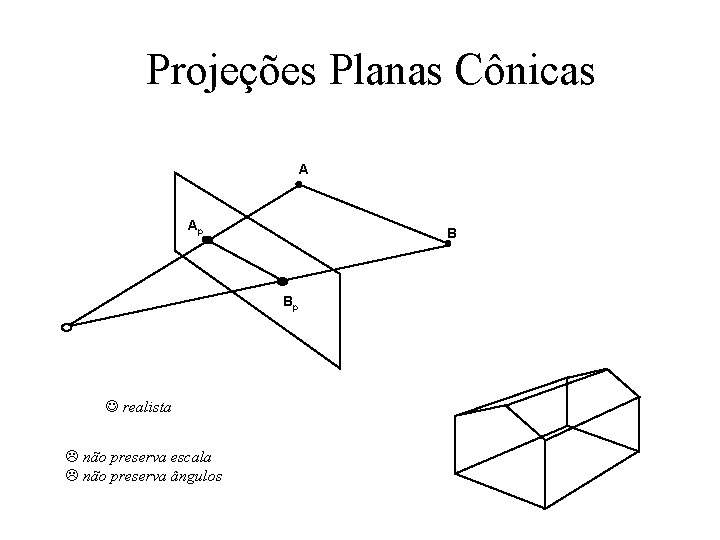
Projeções Planas Cônicas A Ap B Bp J realista L não preserva escala L não preserva ângulos

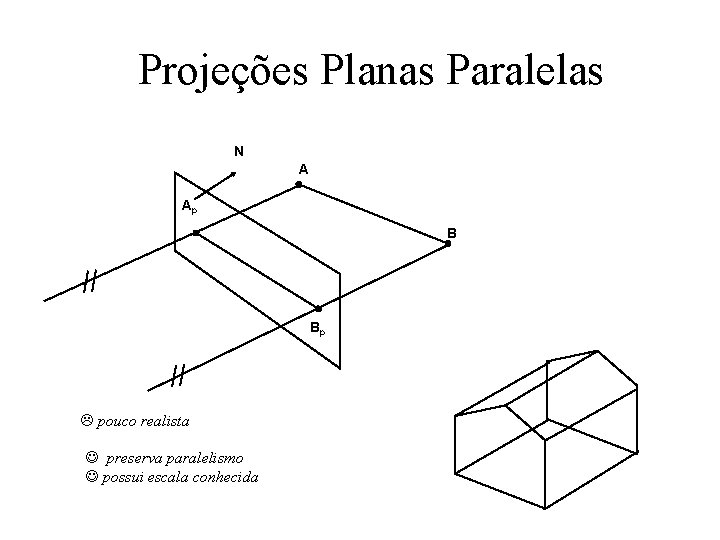
Projeções Planas Paralelas N A Ap B Bp L pouco realista J preserva paralelismo J possui escala conhecida

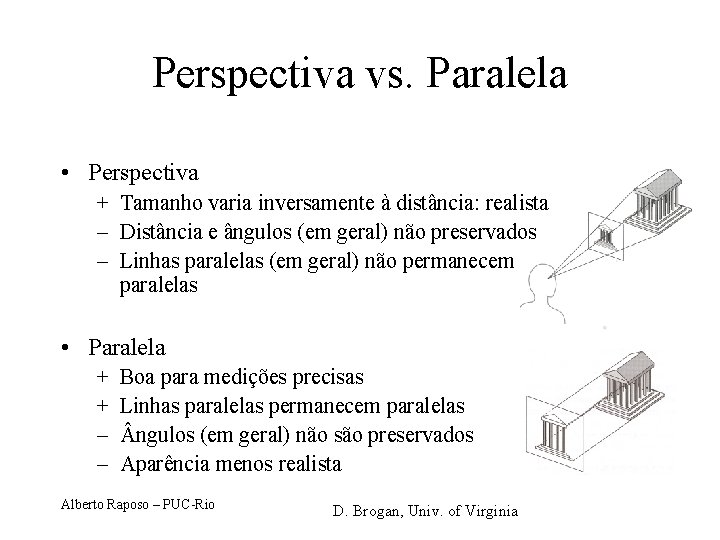
Perspectiva vs. Paralela • Perspectiva + Tamanho varia inversamente à distância: realista – Distância e ângulos (em geral) não preservados – Linhas paralelas (em geral) não permanecem paralelas • Paralela + + – – Boa para medições precisas Linhas paralelas permanecem paralelas ngulos (em geral) não são preservados Aparência menos realista Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

Taxonomia de Projeções Alberto Raposo – PUC-Rio

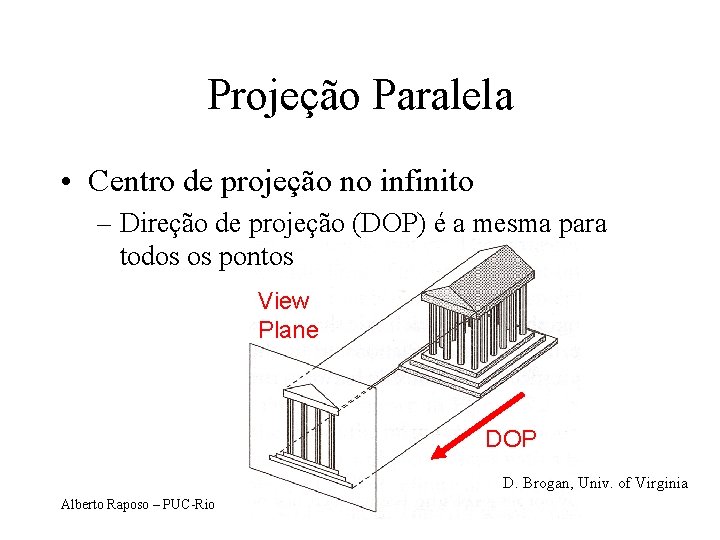
Projeção Paralela • Centro de projeção no infinito – Direção de projeção (DOP) é a mesma para todos os pontos View Plane DOP D. Brogan, Univ. of Virginia Alberto Raposo – PUC-Rio

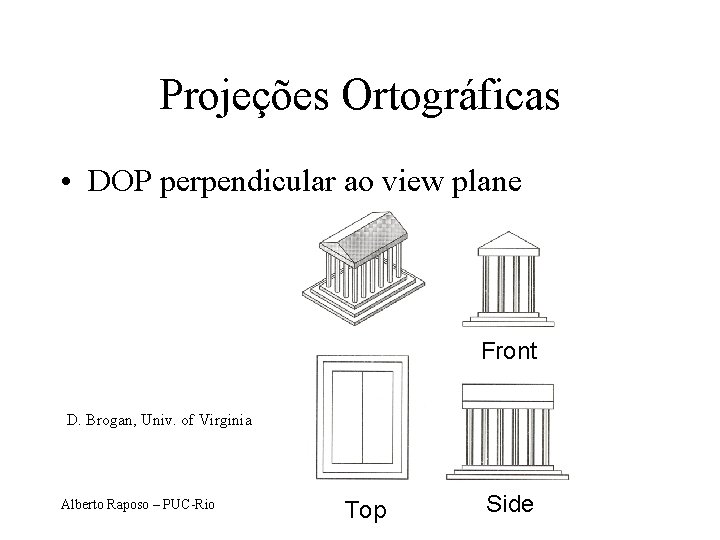
Projeções Ortográficas • DOP perpendicular ao view plane Front D. Brogan, Univ. of Virginia Alberto Raposo – PUC-Rio Top Side

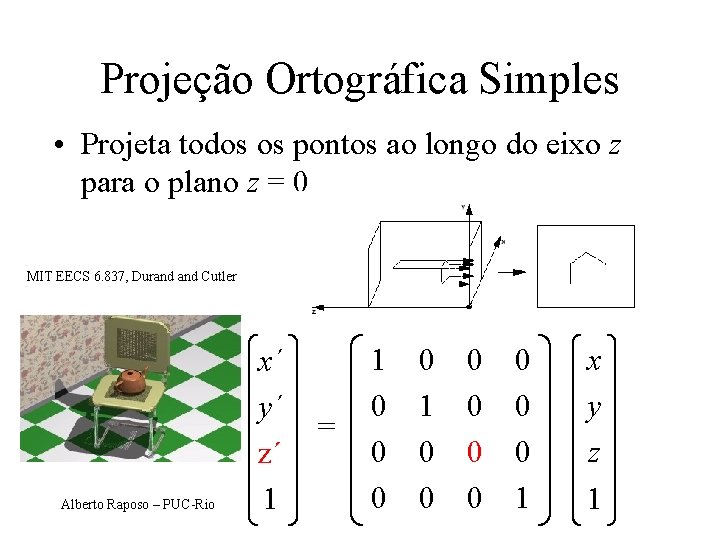
Projeção Ortográfica Simples • Projeta todos os pontos ao longo do eixo z para o plano z = 0 MIT EECS 6. 837, Durand Cutler Alberto Raposo – PUC-Rio x´ y´ z´ 1 = 1 0 0 0 0 1 x y z 1

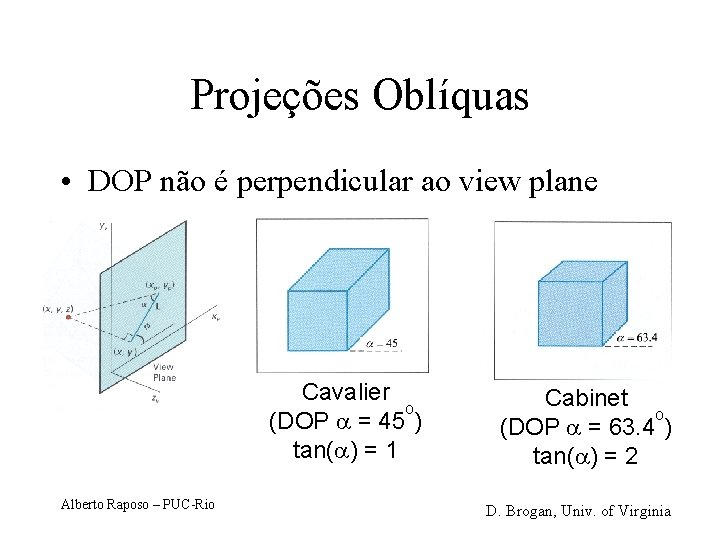
Projeções Oblíquas • DOP não é perpendicular ao view plane Cavalier o (DOP = 45 ) tan( ) = 1 Alberto Raposo – PUC-Rio Cabinet o (DOP = 63. 4 ) tan( ) = 2 D. Brogan, Univ. of Virginia

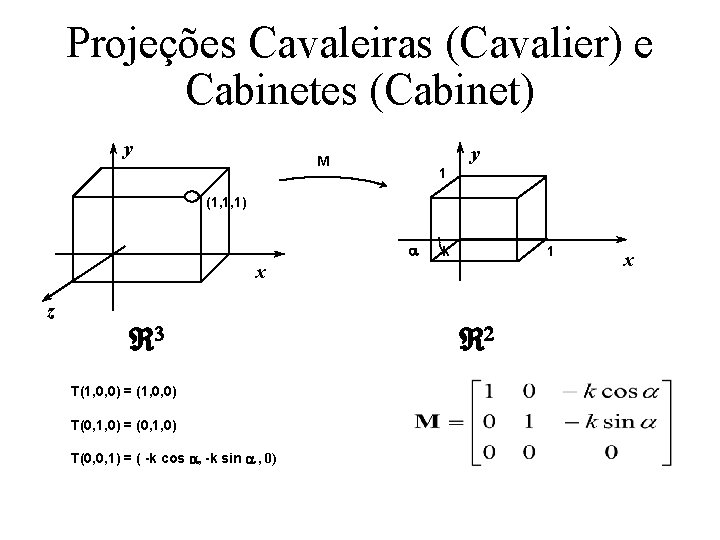
Projeções Cavaleiras (Cavalier) e Cabinetes (Cabinet) y y M 1 (1, 1, 1) a k 1 x z 3 T(1, 0, 0) = (1, 0, 0) T(0, 1, 0) = (0, 1, 0) T(0, 0, 1) = ( -k cos a, -k sin a , 0) 2 x

Taxonomia de Projeções Alberto Raposo – PUC-Rio

Transformação Perspectiva MIT EECS 6. 837, Durand Cutler • Descoberta por Donatello, Brunelleschi, e Da. Vinci durante o Renascentismo • Objetos mais próximos parecem maiores • Linhas paralelas convergem em um único ponto (ponto de fuga) Alberto Raposo – PUC-Rio

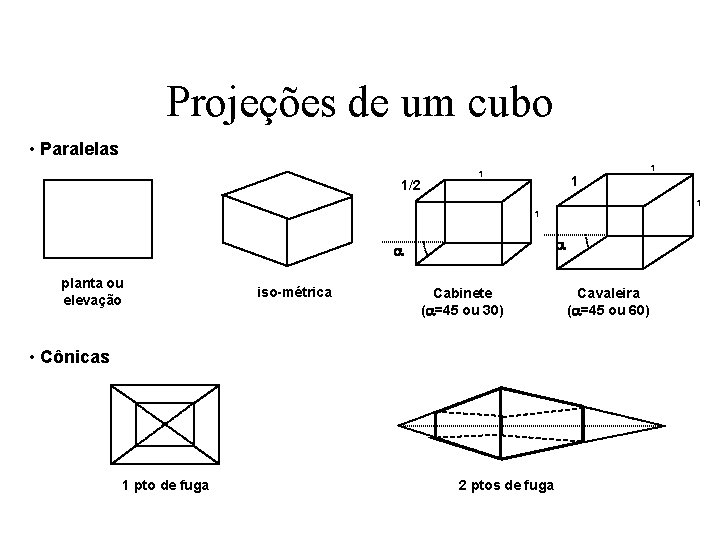
Projeções de um cubo • Paralelas 1/2 1 1 1 a a planta ou elevação iso-métrica Cabinete (a=45 ou 30) • Cônicas 1 pto de fuga 2 ptos de fuga Cavaleira (a=45 ou 60)

Projeções Clássicas D. Brogan, Univ. of Virginia Alberto Raposo – PUC-Rio

Projeção Perspectiva • Quantos pontos de fuga? 3 -Point Perspective 2 -Point Perspective 1 -Point Perspective D. Brogan, Univ. of Virginia Alberto Raposo – PUC-Rio

Perspectiva na pintura Filippo Lippi, La Anunciación (1442) (sem perspectiva) Alberto Raposo – PUC-Rio (com perspectiva)

Projeções Cônicas e Ponto de Fuga Vermeer, “La lección de música” Alberto Raposo – PUC-Rio

Projeção cônica f Alberto Raposo – PUC-Rio

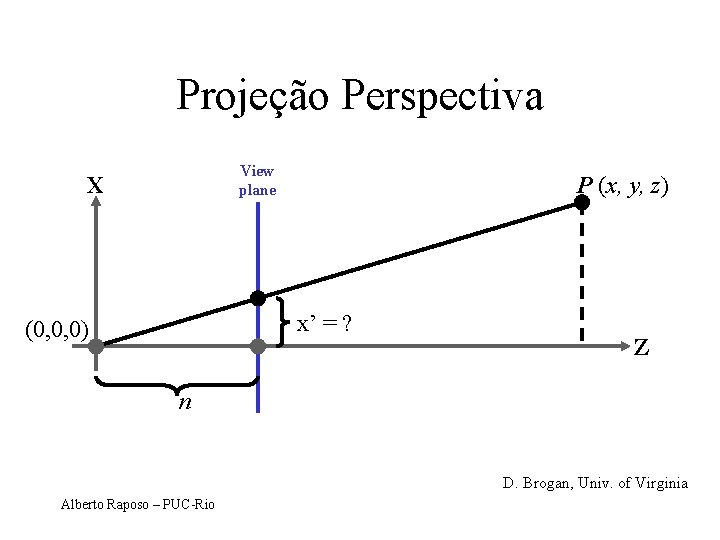
Projeção Perspectiva View plane X P (x, y, z) x’ = ? (0, 0, 0) Z n D. Brogan, Univ. of Virginia Alberto Raposo – PUC-Rio

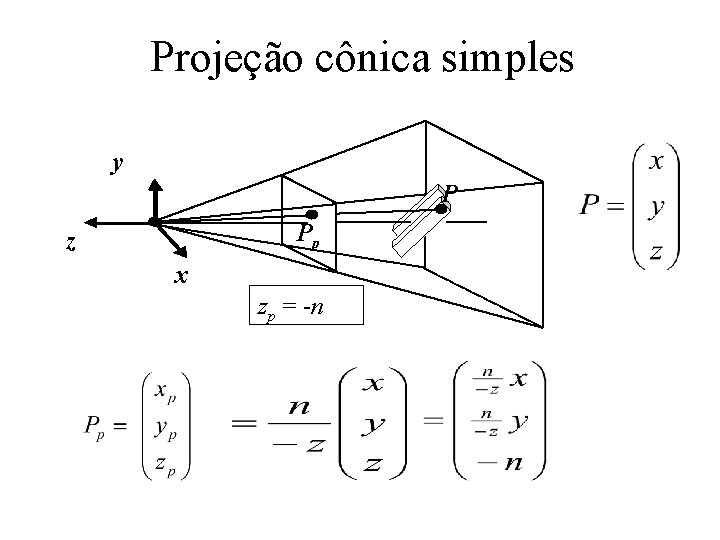
Projeção cônica simples y P Pp z x zp = -n

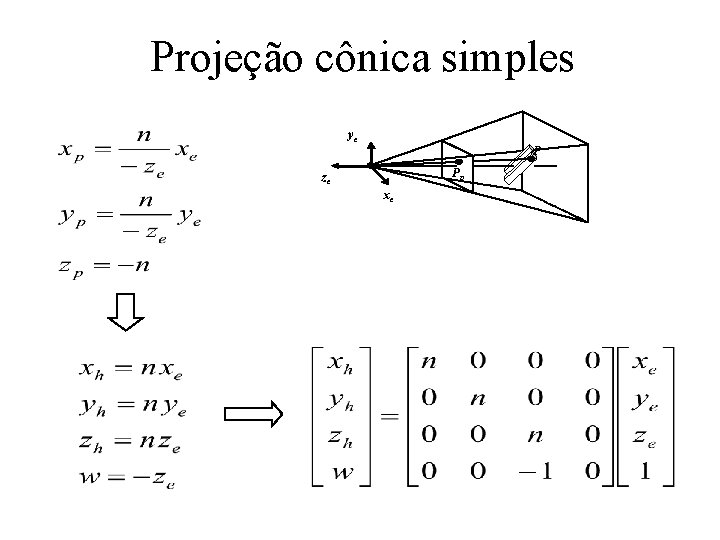
Projeção cônica simples ye P Pp ze xe

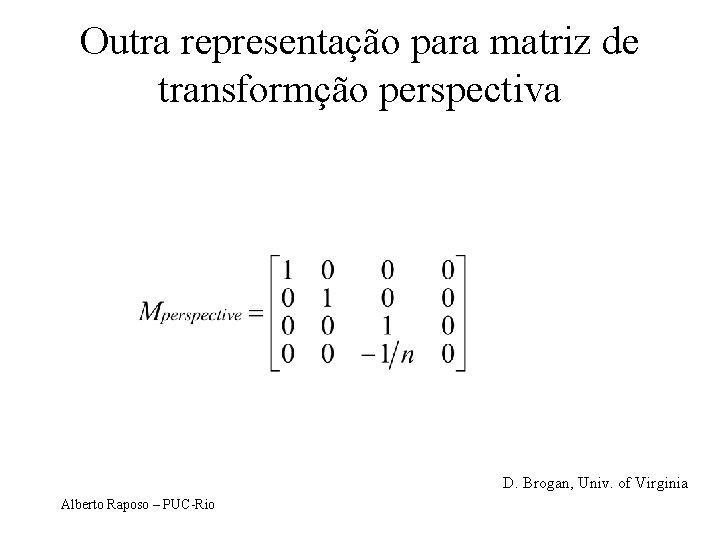
Outra representação para matriz de transformção perspectiva D. Brogan, Univ. of Virginia Alberto Raposo – PUC-Rio

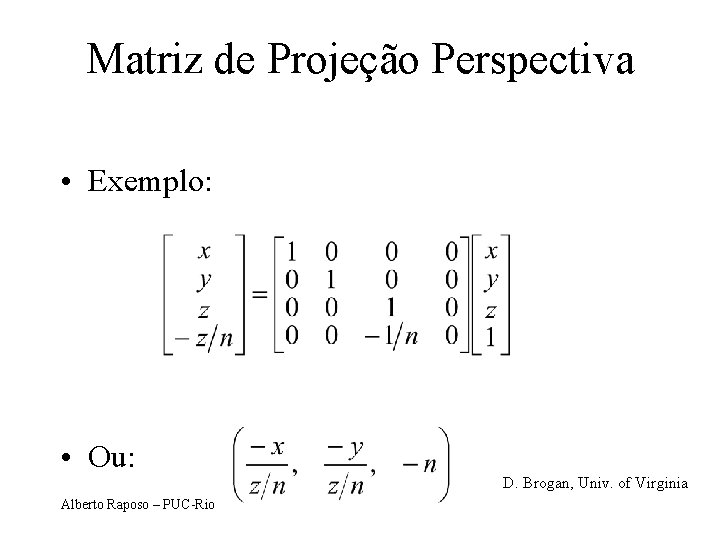
Matriz de Projeção Perspectiva • Exemplo: • Ou: Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

No limite, n → ∞ A matriz de projeção perspectiva. . . 1 0 0 0 1/n . . . é a de projeção ortográfica 0 0 0 1 → MIT EECS 6. 837, Durand Cutler Alberto Raposo – PUC-Rio - 1 0 0 0 0 1

Câmera Virtual – Computação Gráfica Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

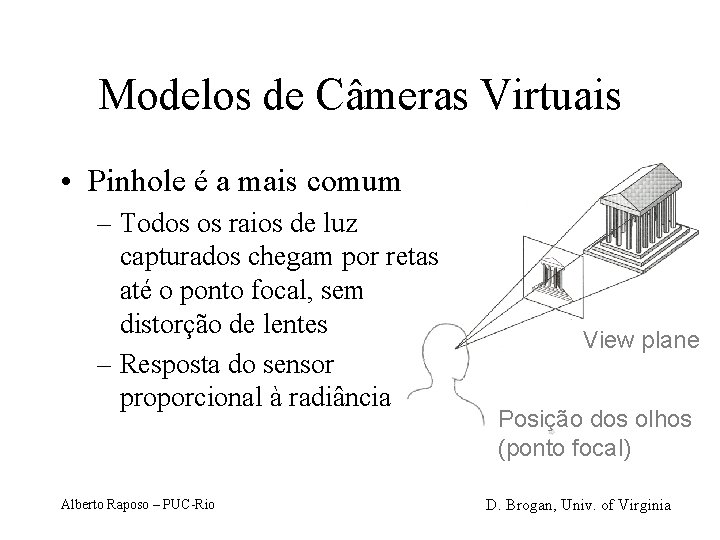
Modelos de Câmeras Virtuais • Pinhole é a mais comum – Todos os raios de luz capturados chegam por retas até o ponto focal, sem distorção de lentes – Resposta do sensor proporcional à radiância Alberto Raposo – PUC-Rio View plane Posição dos olhos (ponto focal) D. Brogan, Univ. of Virginia

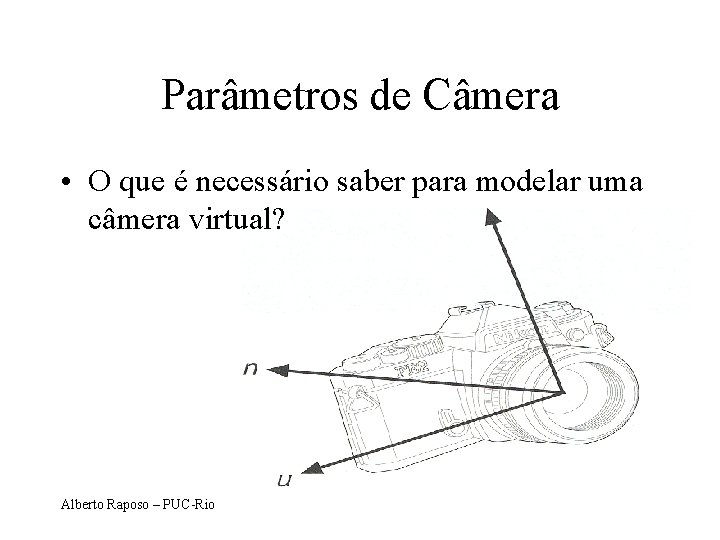
Parâmetros de Câmera • O que é necessário saber para modelar uma câmera virtual? Alberto Raposo – PUC-Rio

Sistemas de Coordenadas • Do mundo (world coordinates): ponto arbitrário no espaço, a partir do qual o mundo é modelado • De câmera (eye coordinates): centrado na posição do observador, com o eixo “-z” na direção para onde se olha e o eixo “y” naquilo que se define como “para cima” Alberto Raposo – PUC-Rio

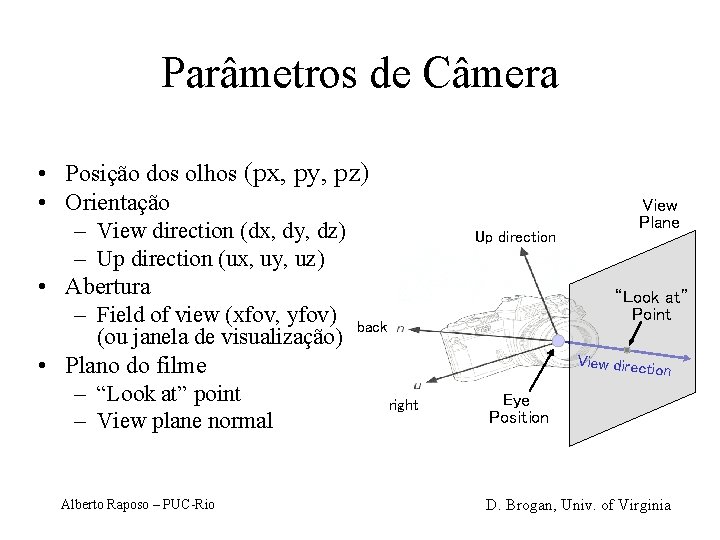
Parâmetros de Câmera • Posição dos olhos (px, py, pz) • Orientação – View direction (dx, dy, dz) – Up direction (ux, uy, uz) • Abertura – Field of view (xfov, yfov) back (ou janela de visualização) • Plano do filme – “Look at” point – View plane normal Alberto Raposo – PUC-Rio Up direction View Plane “Look at” Point View directio n right Eye Position D. Brogan, Univ. of Virginia

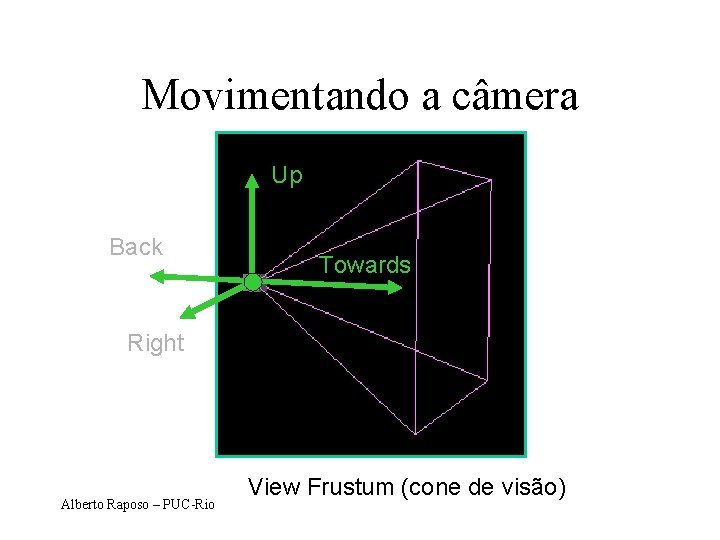
Movimentando a câmera Up Back Towards Right Alberto Raposo – PUC-Rio View Frustum (cone de visão)

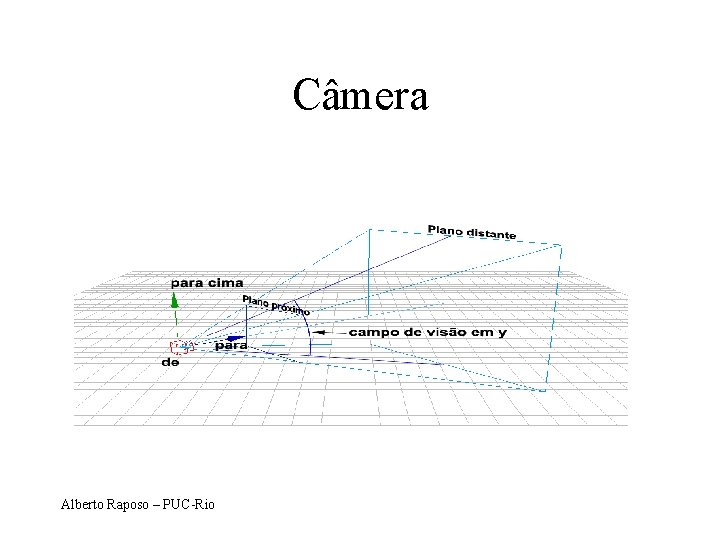
Câmera Alberto Raposo – PUC-Rio

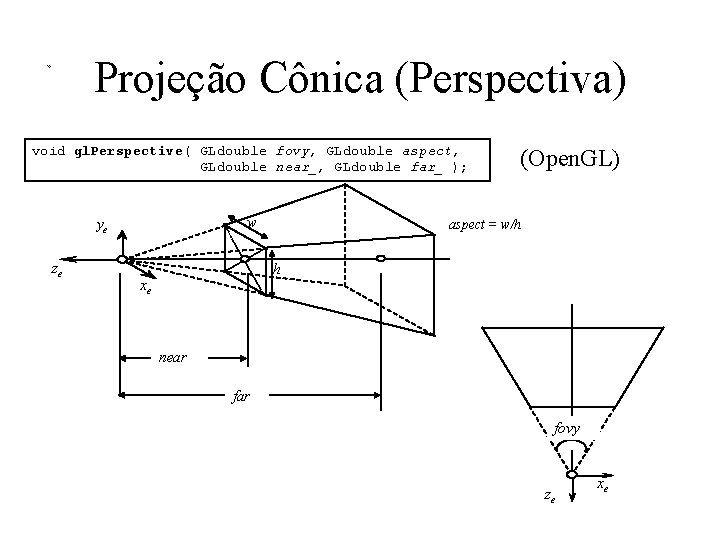
Projeção Cônica (Perspectiva) void gl. Perspective( GLdouble fovy, GLdouble aspect, GLdouble near_, GLdouble far_ ); w ye ze (Open. GL) aspect = w/h h xe near fovy ze xe

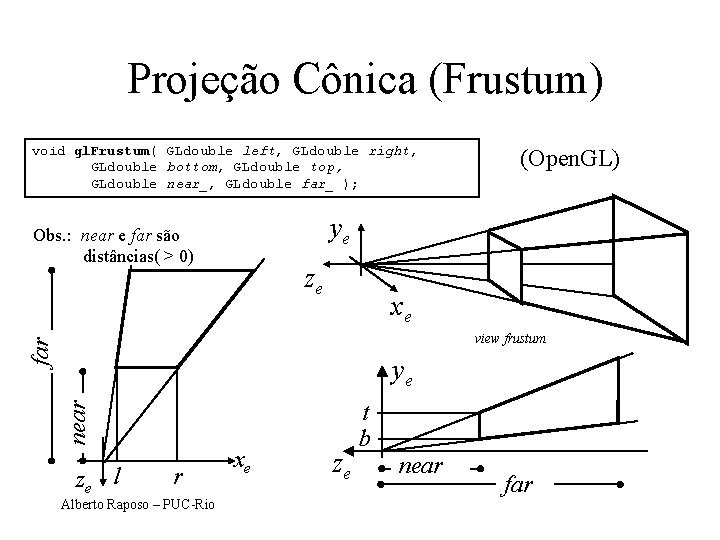
Projeção Cônica (Frustum) void gl. Frustum( GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near_, GLdouble far_ ); (Open. GL) ye Obs. : near e far são distâncias( > 0) ze xe far view frustum near ye ze l r Alberto Raposo – PUC-Rio xe ze t b near far

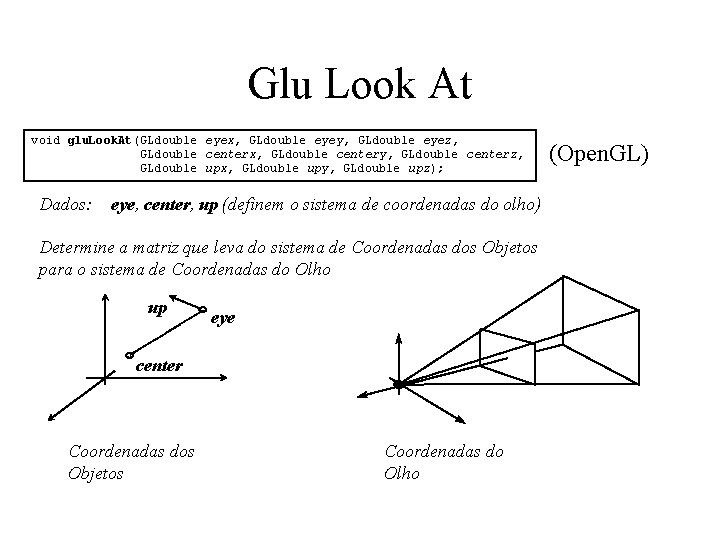
Glu Look At void glu. Look. At(GLdouble eyex, GLdouble eyey, GLdouble eyez, GLdouble centerx, GLdouble centery, GLdouble centerz, GLdouble upx, GLdouble upy, GLdouble upz); Dados: eye, center, up (definem o sistema de coordenadas do olho) Determine a matriz que leva do sistema de Coordenadas dos Objetos para o sistema de Coordenadas do Olho up eye center Coordenadas dos Objetos Coordenadas do Olho (Open. GL)

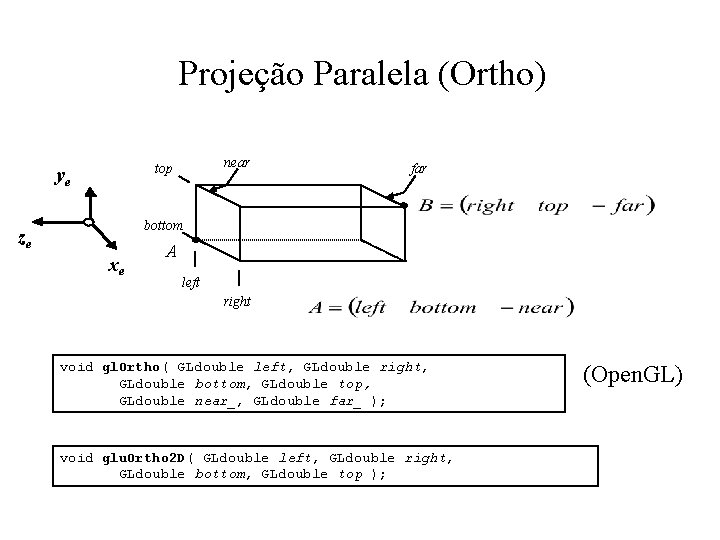
Projeção Paralela (Ortho) near top ye far bottom ze xe A left right void gl. Ortho( GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near_, GLdouble far_ ); void glu. Ortho 2 D( GLdouble left, GLdouble right, GLdouble bottom, GLdouble top ); (Open. GL)

Câmera VRML: Viewpoint Alberto Raposo – PUC-Rio

Exemplo VRML Alberto Raposo – PUC-Rio

Exemplo VRML The Annotated VRML Reference Alberto Raposo – PUC-Rio

Exemplo VRML The Annotated VRML Reference Alberto Raposo – PUC-Rio

Exemplo VRML The Annotated VRML Reference Alberto Raposo – PUC-Rio

Exemplo VRML The Annotated VRML Reference Alberto Raposo – PUC-Rio

Exemplo X 3 D Alberto Raposo – PUC-Rio

Transformações de Visualização • Cria-se uma visualização centrada na câmera • Câmera está na origem • Câmera olha para o eixo z no sentido negativo • O ‘up’ é alinhado com o eixo y Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

2 Passos básicos • Alinha-se os sistemas de coordenadas (de câmera e do mundo) por rotação Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

2 Passos básicos • Translação para alinhar as origens Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

Espaço de coordenadas da câmera • Especifica-se ponto onde a câmera está localizada (origem do espaço) eye point • Especifica-se ponto onde será o centro da visualizaçãolookat point • Especifica-se o vetor “up” up vector • Movimentos intuitivos da câmera Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

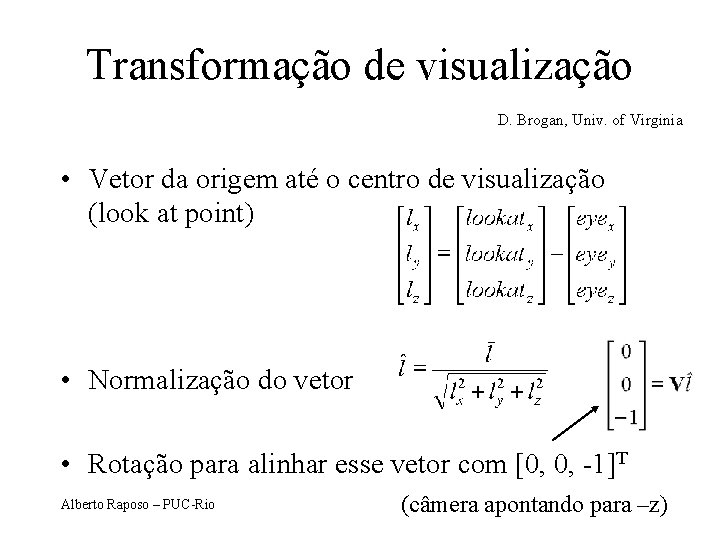
Transformação de visualização D. Brogan, Univ. of Virginia • Vetor da origem até o centro de visualização (look at point) • Normalização do vetor • Rotação para alinhar esse vetor com [0, 0, -1]T Alberto Raposo – PUC-Rio (câmera apontando para –z)

Transformação de visualização • Se lookat-vector deve se alinhar com –z e o vup-vector se alinha com y: • Esse vetor, normalizado, deve alinhar-se com [1, 0, 0]T Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

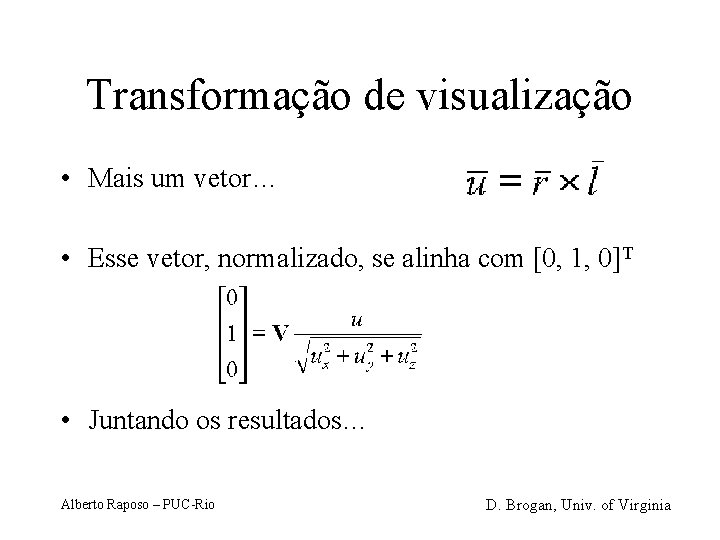
Transformação de visualização • Mais um vetor… • Esse vetor, normalizado, se alinha com [0, 1, 0]T • Juntando os resultados… Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

Compondo vetores para formar a matriz V • Conhecemos os eixos de coordenadas do mundo (x, y, z) • E também os eixos da câmera (r, u, l) • A transfomação de visualização, V, deve converter o sistema do mundo para o sistema da câmera Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

Compondo vetores para formar a matriz V • Cada eixo da câmera é de módulo unitário • Cada eixo é perpendicular aos demais • A matriz de câmera é ortogonal e normalizada – Ortonormal • Matriz ortonormal: M-1 = MT Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

Compondo vetores para formar a matriz V • Logo, a componente de rotação da matriz de transformação de visualização … . . . é simplesmente a transposta Alberto Raposo – PUC-Rio D. Brogan, Univ. of Virginia

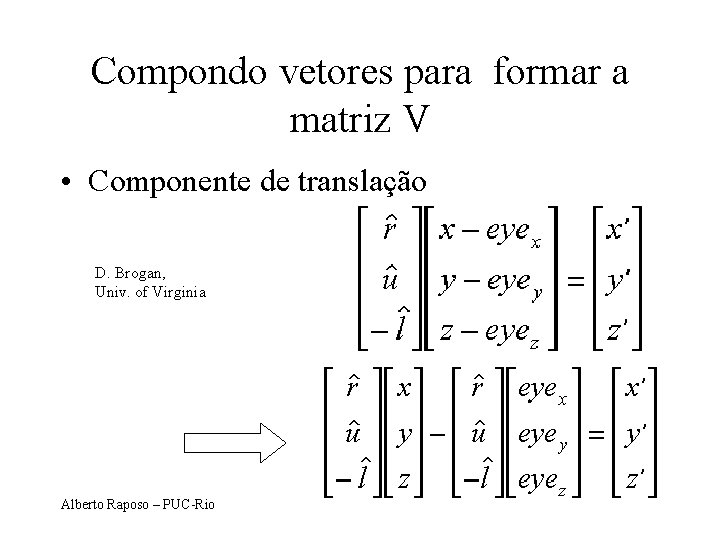
Compondo vetores para formar a matriz V • Componente de translação D. Brogan, Univ. of Virginia Alberto Raposo – PUC-Rio

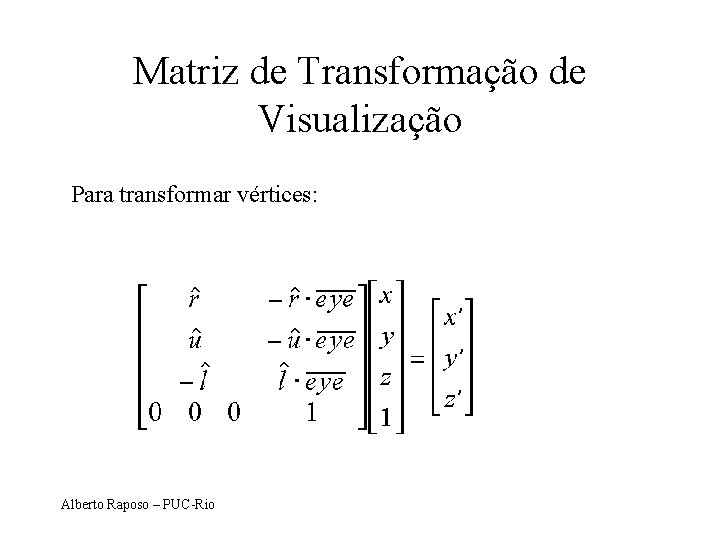
Matriz de Transformação de Visualização Para transformar vértices: Alberto Raposo – PUC-Rio

Informações Adicionais – Peter Shirley. Fundamentals of Computer Graphics, A K Peters, Ltd. , Natick, MA, USA, 2002. – Foley, J. D. , Van Dam, A. , Feiner, S. K. , e Huhes, J. F. , Phlips, L. R. , Introduction to Computer Graphics, Addison-Wesley, 1995. – D. F. Rogers, J. A. Adams. “Mathematical Elements for Computer Graphics”. 2 nd Ed. , Mc. Graw-Hill, 1990. Alberto Raposo – PUC-Rio