HMM Applications Mark Stamp HMM Applications 1 Applications

HMM Applications Mark Stamp HMM Applications 1

Applications q Applications not chosen because they are the most ingenious or clever q Instead, we want straightforward o Applications illustrate the basics o Show off the strengths of techniques o Easy to understand appreciate q Academic publications usually favor novel, different, clever, (weird? ), … HMM Applications 2

HMM for English Text Analysis Mark Stamp HMM Applications 3

Marvin the Martian q Marvin the Martian arrives on earth o Marvin sees written English text o Wants to learn something about it o Martians know HMMs, but not English q So, strip out all non-letters, make all letters lower-case o 27 symbols (26 letters, word-space) o Train HMM on long sequence of “symbols” HMM Applications 4

Training q For first training case, initialize o N = 2 and M = 27 o Elements of A and π are all approx 1/2 o Elements of B are each about 1/27 q We’ll use 50, 000 symbols for training q After 1 st iter: log P(O|λ) ≈ -165097 q After 100 th iter: log P(O|λ) ≈ -137305 HMM Applications 5

The A and π Matrices q What A and π converge to: does this tells us? o Started in hidden state 1 (not state 0) o And we know transition probabilities between hidden states q Nothing too interesting here o We don’t (yet) know about hidden states HMM Applications 6

The B Matrix (Transpose) q What does B matrix tell us? q This is very interesting! o Why? ? ? HMM Applications 7

Conclusion q The B matrix tells Marvin about consonants and vowels q He made no assumption a priori q The training itself “learned” this info q This is the essence of machine learning! o We don’t have to think too much o Machine does all the hard work o Machine “learns” (and so do we) HMM Applications 8

Detecting “Undetectable” Malware Sujan Venkatachalam Mark Stamp HMM Applications 9

Malware & Detection q Malware is malicious software o Designed to do bad things q Most common form of detection is based on signatures o What is a signature? q Malware writers try to avoid detection o How to avoid signature detection? o One option is to morph/modify code HMM Applications 10

Metamorphic Malware q Malware that morphs with each new infection is called “metamorphic” q How to write metamorphic malware? o Standalone generator vs malware that “carries its own morphing engine” q How to detect metamorphic malware? o Also not easy, it’s a research topic o Machine learning (masters projects) HMM Applications 11

Background q. A paper gave a design for a metamorphic malware generator o They proved that resulting malware is not detectable using signatures o Sounds fancy, but actually simple idea q We implemented this generator o We know signature detection won’t work o So, let’s try machine learning… HMM Applications 12

Code Morphing q From a high level, we can morph code using some combination of. . . o Transposition, subst. , insertion, deletion q The signature-proof metamorphic generator relies only on transposition o And inserted jmp instructions, so that code executes in the original order o This is a simple but effective idea HMM Applications 13

Real-World Metamorphism q Examples of metamorphic malware q Why “garbage code” (or “dead code”)? q Why is substitution not used more? HMM Applications 14

Metamorphic Example q From malware known as NGVCK q 3 morphed versions o All do the same thing o Each has different opcode sequence o What can you say about signature(s)? HMM Applications 15

Our Metamorphic Generator q Signature-proof metamorphic generator q Initialize with a seed virus o In the form of assembly code q Split into small blocks o Blocks are 6 lines of code, on average o Blocks subject to some conditions q To generate a malware sample… o Shuffle code blocks, add conditional jumps HMM Applications 16

Metamorphic Generator q Shuffling blocks will break signatures q Can vary size of blocks as needed q Optionally, include dead code insertion o Inserted between actual code blocks o We use “opaque predicates” q Why insert dead code? o Makes statistical analysis more difficult o Analysis in general is more difficult HMM Applications 17

Experiments q Seed the generator with NGVCK virus q Generated 200 morphed copies o Assemble each morphed asm into exe o Verify that seed virus detected by AV… o …and morphed copies not detected by AV q Disassemble exes, extract opcodes o Train HMMs, using 5 -fold cross validation o Score each model vs 40 benign samples HMM Applications 18

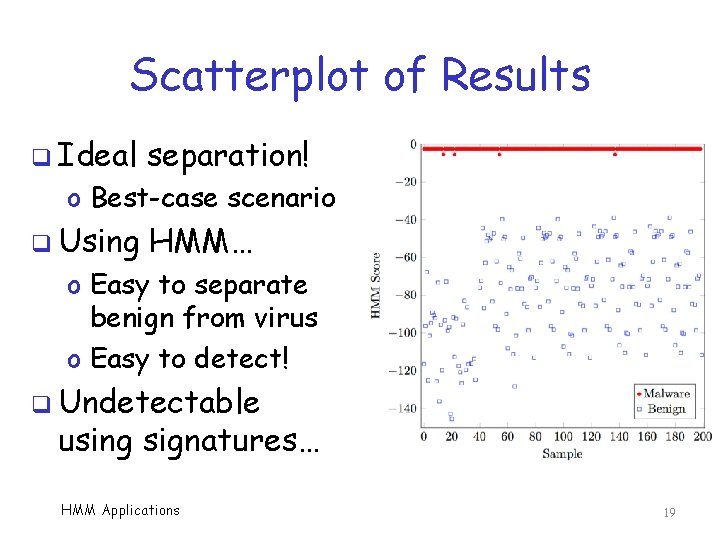
Scatterplot of Results q Ideal separation! o Best-case scenario q Using HMM… o Easy to separate benign from virus o Easy to detect! q Undetectable using signatures… HMM Applications 19

What’s Going On Here? q Why can we detect this morphed malware using HMMs o But not using signatures? q Signatures are easily disrupted by simple transposition strategy q HMM not affected by transposition o HMM “sees” differences between viruses and benign, in spite of this morphing HMM Applications 20

Conclusion q Transposition is highly effective antisignature strategy q But ineffective for machine learning (or statistical-based) analysis q Can virus writer defeat both signatures and machine learning? o Yes, but something more is required… o We’ll have more to say about this later HMM Applications 21

Classic Cryptanalysis Rohit Vobbilisetty Mark Stamp HMM Applications 22

Overview q Here, we consider classic ciphers o We want to cryptanalyze (break) ciphers q We show that HMM is a useful tool q HMM is a hill climb o Can only find local maximum o Max we find depends on starting point q Here, we analyze effectiveness of HMMs with multiple random restarts HMM Applications 23

Classic Ciphers q In this section, we consider simple and homophonic substitution ciphers o We’ll assume the plaintext is English q Simple substitution uses 1 -1 mapping o One ciphertext symbol for each plaintext q Homophonic cipher allows for many-to-one o More than one ciphertext symbol can map to a single plaintext symbol q Advantage(s) of homophonic substitution? HMM Applications 24

Simple Substitution Example q Plaintext: fourscoreandsevenyearsago q Key: Plaintext a b c d e f g h i j k l m n o p q r s t u v w x y z Ciphertext D E F G H I J K L M N O P Q R S T U V W X Y Z A B C q Ciphertext: IRXUVFRUHDQGVHYHQBHDUVDJR q Shift by 3 is “Caesar’s cipher” HMM Applications 25

Simple Substitution q In general, simple substitution key can be any permutation of the alphabet q Alice and Bob both know the key, so they can send “secret” messages q Bad guy, Trudy, sees ciphertext o We assume Trudy does not know the key q Can Trudy use ciphertext to find the plaintext and/or key? HMM Applications 26

Simple Substitution Cryptanalysis Cannot try all simple substitution keys q Can we be more clever? q Yes! Use English letter frequencies q HMM Applications 27

Simple Substitution q Trudy can use frequency counts to break simple substitution cipher q Most common letter in English is “E” o So, most common letter in ciphertext probably corresponds to plaintext “E” q Next is “A” then “T” then … o Some work and trial-and-error required o But statistical analysis can succeed HMM Applications 28

Homophonic Substitution q Advantage of homophonic substitution? q Suppose 3 ciphertexts map to “E” o Each time “E” is to be encrypted, randomly choose from the 3 ciphertexts q Then ciphertext stats more uniform o Harder for Trudy to determine plaintext letters from ciphertext o But still easy to decrypt message with key HMM Applications 29

Simple Substitution q Hill climb to break simple substitution q Three things we must be able to do… o Make initial guess for putative key o Modify putative key in systematic way o Score a putative key q Initial putative key? o Use letter frequency counts. . . o. . . since nothing better to start with HMM Applications 30

Simple Substitution q How to modify putative key? o Let K = (k 1, k 2, …, k 26), then swap as. . . o And restart each time score improves HMM Applications 31

Simple Substitution q How to score a putative key? o Dictionary words in putative decryption? o Better way is to use English digraphs HMM Applications 32

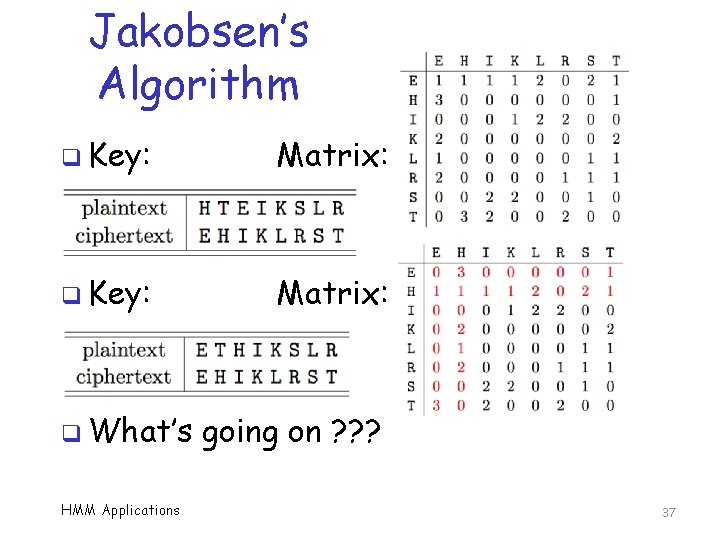
Jakobsen’s Algorithm q Fast hill climb attack on simple sub. q Uses approach just described… q But with a clever scoring algorithm q Example using 8 letter alphabet: EHIKLRST q Suppose ciphertext is HTHEIHEILIRKSHEIRLHKTISRRKSIIKLIEHTTRLHKTIS q Initial HMM Applications key based on frequency counts 33

Jakobsen’s Algorithm q Suppose ciphertext is HTHEIHEILIRKSHEIRLHKTISRRKSIIKLIEHTTRLHKTIS q Initial key based on frequency counts EHIKLRST 47954545 q So, we choose initial key HMM Applications 34

Jakobsen’s Algorithm q Using this key and ciphertext HTHEIHEILIRKSHEIRLHKTISRRKSIIKLIEHTTRLHKTIS q Then, putative decryption is TRTHETHEKESILTHESKTIRELSSILEEIKEHTRRSKTIREL q Gives us the digraph distribution matrix HMM Applications 35

Jakobsen’s Algorithm q If instead, putative key is q Then digraph distribution matrix is HMM Applications 36

Jakobsen’s Algorithm q Key: Matrix: q What’s HMM Applications going on ? ? ? 37

Jakobsen’s Algorithm q Swap 1 st and 2 nd elements of key… q Has effect of swapping 1 st and 2 nd rows and columns of digraph matrix q This makes Jakobsen’s algorithm fast q No need to decrypt again when key is modified just swap rows/columns q Very nice trick! HMM Applications 38

Jakobsen’s Algorithm q Let E be the expected digraph distribution matrix for English q Given ciphertext C… q Jakobsen’s Algorithm on next slide. . . HMM Applications 39

Jakobsen’s Algorithm 1. 2. 3. 4. 5. 6. 7. Choose initial K based on frequency counts Find putative decryption, and generate digraph distribution matrix D Compute distance (score) between E and D Swap elements of K following key schedule Swap corresponding rows/columns of D If score improves, keep new K, otherwise leave K as it was before swap Goto 4 (unless at end of key schedule) HMM Applications 40

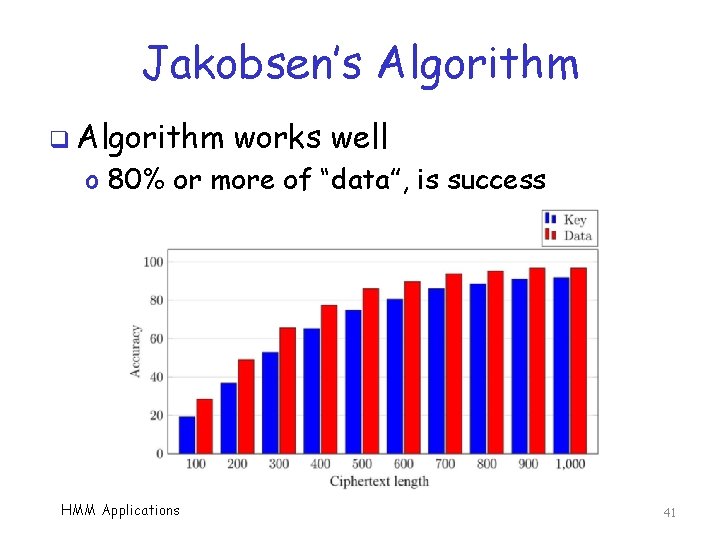
Jakobsen’s Algorithm q Algorithm works well o 80% or more of “data”, is success HMM Applications 41

HMM for Simple Substitution q We can also use HMM to attack simple substitution ciphers! q Recall HMM for English text example o With N=2 states, consonants and vowels q Simple substitution re-labels letters o So, HMM can tell us which letters correspond to consonants vowels q Nice, but we can do much better! HMM Applications 42

HMM for Simple Substitution q Suppose we have N=26 hidden states q Reasonable to think these might correspond to letters A, B, …, Z q If so, then we know what the A matrix should be. . . q We can specify initial A matrix o And no need to re-estimate A matrix q Then what will the B matrix tell us ? ? ? HMM Applications 43

HMM Simple Substitution q Initial q Final B matrix: HMM Applications 44

HMM for Simple Substitution q How does HMM compare to Jakobsen’s for simple substitution cryptanalysis? o Answer: Not good q But, if we do multiple random restarts, HMM can do better than Jakobsen’s o Useful in cases where data is limited o That is, ciphertext message is short HMM Applications 45

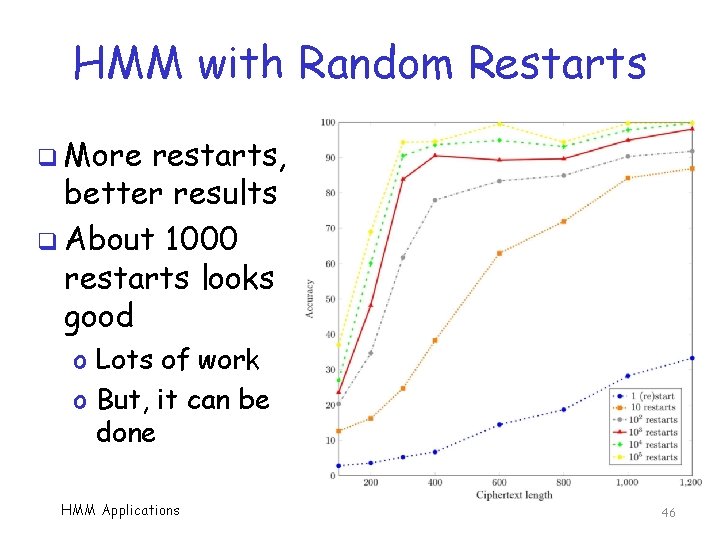
HMM with Random Restarts q More restarts, better results q About 1000 restarts looks good o Lots of work o But, it can be done HMM Applications 46

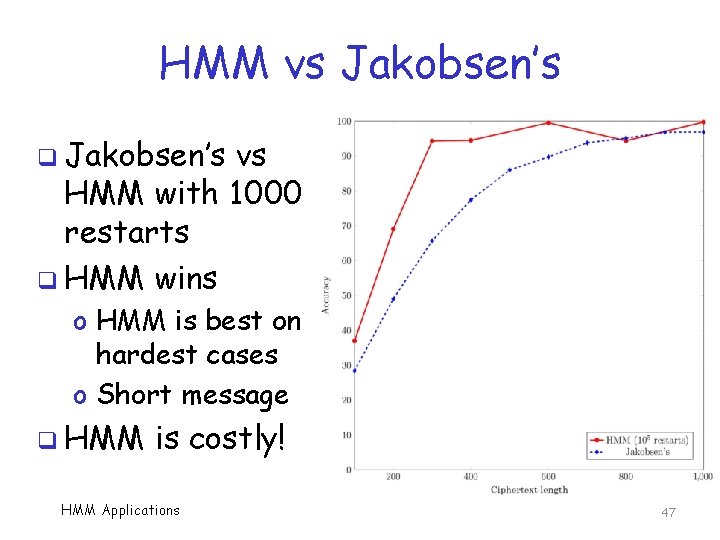
HMM vs Jakobsen’s q Jakobsen’s vs HMM with 1000 restarts q HMM wins o HMM is best on hardest cases o Short message q HMM is costly! HMM Applications 47

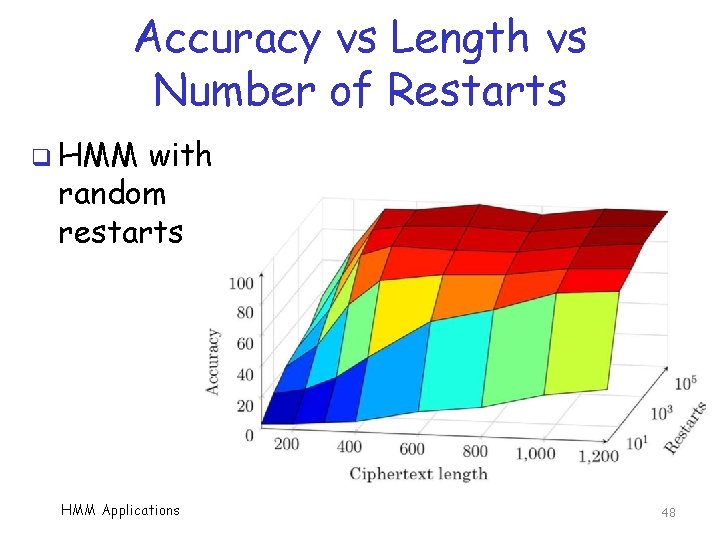
Accuracy vs Length vs Number of Restarts q HMM with random restarts HMM Applications 48

Homophonic Substitution q Recall homophonic substitution has many-to-one mapping q More than one ciphertext symbol can map to one plaintext symbol q Can Jakobsen’s Algorithm be modified to work on homophonic substitution? q Can HMM (with random restarts) break homophonic substitution? HMM Applications 49

Jakobsen’s for Homophonic Substitution q. A student developed a nested hill climb for homophonic substitution o Based on Jakobsen’s Algorithm q Much slower/costlier than Jakobsen’s q Reasonably effective for fairly small number of ciphertext symbols q Improved by another researcher o 5 x faster, but still not all that fast HMM Applications 50

HMM for Homophonic Substitution q The A matrix has English digraph stats o As in simple substitution case (and in Jakobsen’s Algorithm) o This matrix is fixed, not re-estimated q The B matrix has M columns, where M is number of ciphertext symbols q Does this work? q Yes, but… HMM Applications 51

HMM for Homophonic Substitution q Converged B matrix o Sideways… o All probabilities > 0. 1 are in red q What’s here? going on HMM Applications 52

HMM for Homophonic Substitution q In this example, actual key was q Easy to recover this key from B matrix on previous slide o Not so easy in every case HMM Applications 53

Homophonic Substitution q Why would anybody care about homophonic substitutions? q Zodiac Killer murdered several people in San Francisco area in late 1960’s q He sent letters taunting police for not catching him q Police had a suspect, but nobody was ever convicted of the murders HMM Applications 54

Zodiac 408 Cipher q Solved within a few days o By school teachers from Salinas q Homophonic substitution HMM Applications 55

Zodiac 340 Cipher q This one remains unsolved today q Looks like homophonic substitution q But must be more complex o Any ideas? HMM Applications 56

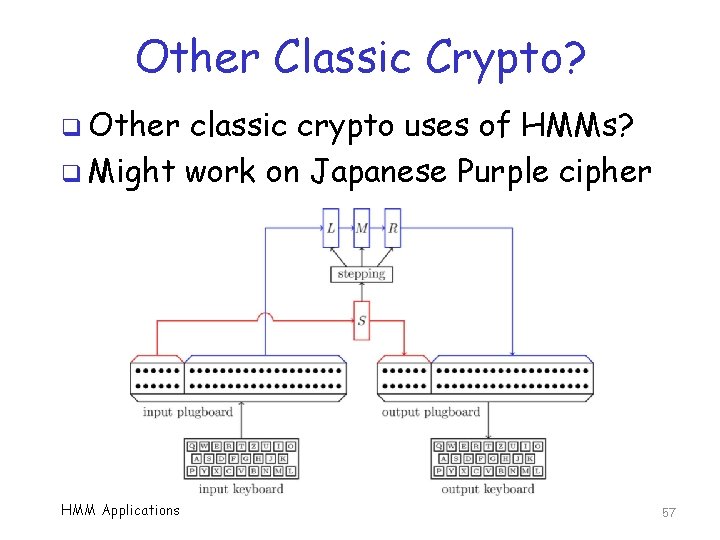
Other Classic Crypto? q Other classic crypto uses of HMMs? q Might work on Japanese Purple cipher HMM Applications 57

References R. L. Cave and L. P. Neuwirth, Hidden Markov models for English, IDA-CRD, Princeton, NJ, October 1980 q S. Venkatachalam and M. Stamp, Detecting undetectable metamorphic viruses, Proceedings of 2011 International Conference on Security & Management (SAM '11), pp. 340345 q R. Vobbilisetty, et al, Classic cryptanalysis using HMMs, Cryptologia, 41(1): 1 -28, 2017 q HMM Applications 58