Hash Maps The point of a hash map

Hash Maps: The point of a hash map is to FIND DATA QUICKLY. We use an array because there’s not much faster than finding the kth value in an array DATA ->hash function ->index Hash function used for both STORING AND THEN FINDING LATER

Hash Map Example Student objects: Sobj *stud 1 = new Sobj(“Smith”, ”Sam”, ”Sophomore”, ”ELEG”, 3. 4, 214325919) Sobj *stud 2 = new Sobj(“Kell”, ”Taylor”, ”Freshman”, ”CISC”, 2. 9, 271132414) Sobj *stud 3 = new Sobj(“Smith”, ”Taylor”, ”Freshman”, ”ELEG”, 3. 4, 199321426) (the unique element about each student is their id) Hash function we’ll use is folding with width of 3 Since the original set of data consists of 3 objects, the ideal array size would be 7 (214+325+919)%7 = 2 (271+132+414)%7 = 5 (199+321+426)%7 = 0 0 1 Taylor Smith, Freshman, ELEG, 3. 4, 199321426 2 Sam Smith, Sophomore, ELEG, 3. 4, 214325919 3 4 5 6 Taylor Kell, Freshman, CISC, 2. 9, 271132414 Once students are stored in array, now when I want to find info about a particular student, I take their id, fold it, and go to that index in the array (0(1))! E. g. , what if I wanted to find Sam Smith’s GPA? (214+325+919)%7 = 2, go to index to and get her GPA!

So Far: Arrays: find the kth value, traversing quickly! Linked lists: join, push, pop (stacks) AVL Trees: insert, delete, search in equally efficient time, no extra space Hash. Map: Finding data quickly!!! (at the cost of extra memory)

Binary Heaps What if we’re concerned with finding the most relevant data? A binary heap is a binary tree (2 or fewer subtrees for each node) A heap is structured so that the node with the most relevant data is the root node, the next most relevant as the children of the root, etc. A heap is not a binary search tree A heap does not order its node A heap is a complete tree. Every level but the leaf level is full Leaf level full from left to right Binary Heap – another way to implement a priority queue! 4

Definition of a Binary Heap A tree is a binary heap if It is a complete tree Every level is full except the bottom level The value in the root is the largest of the tree (Or smallest, if the smallest value is the most relevant and that is how you choose to structure your tree) Every subtree is also a binary heap Equivalently, a complete tree is a binary heap if Node value > child value, for each child of the node Note: This use of the word “heap” is entirely different from the heap that is the allocation area in C++ 5

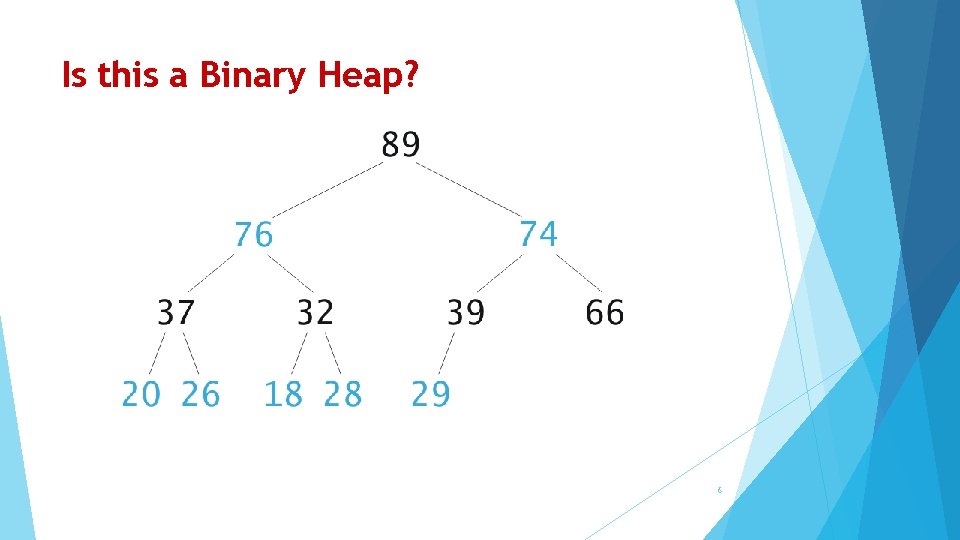
Is this a Binary Heap? 6

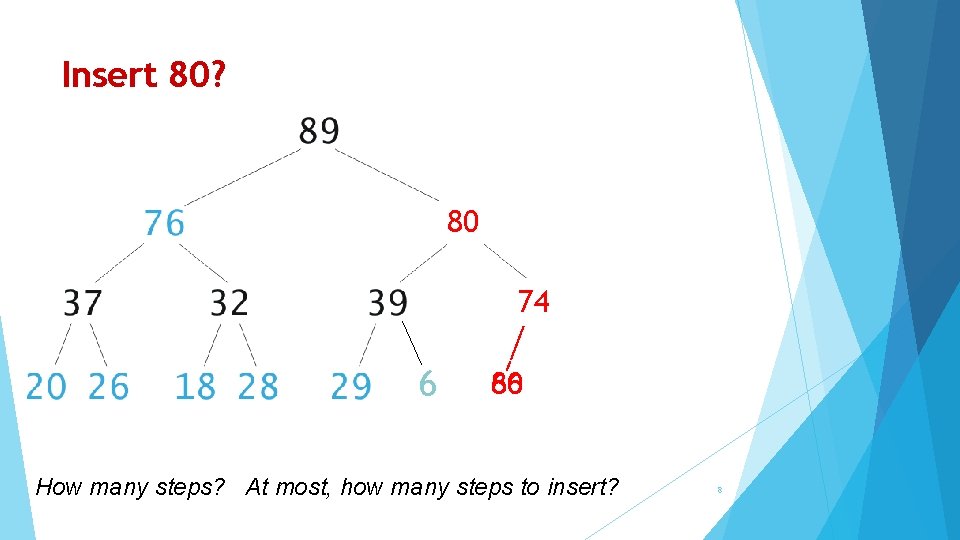
Inserting an Item into a Binary Heap 1. Insert the item in the next position across the bottom of the complete tree: 1. 2. preserves completeness Restore “heap-ness”: 1. 2. while new item is not root and is greater than its parent swap new item with its parent 7

Insert 80? 80 74 80 6 66 80 How many steps? At most, how many steps to insert? 8

Removing an Item We always remove the top (root) node! Heaps find the largest (or smallest) value in a set of numbers and Remove Leaves Fill that number is at the root! the root a “hole”: the “hole” with the last item (lower right-hand leaf) L Preserve Swap completeness L with largest child, as necessary Restore “heap-ness” 9

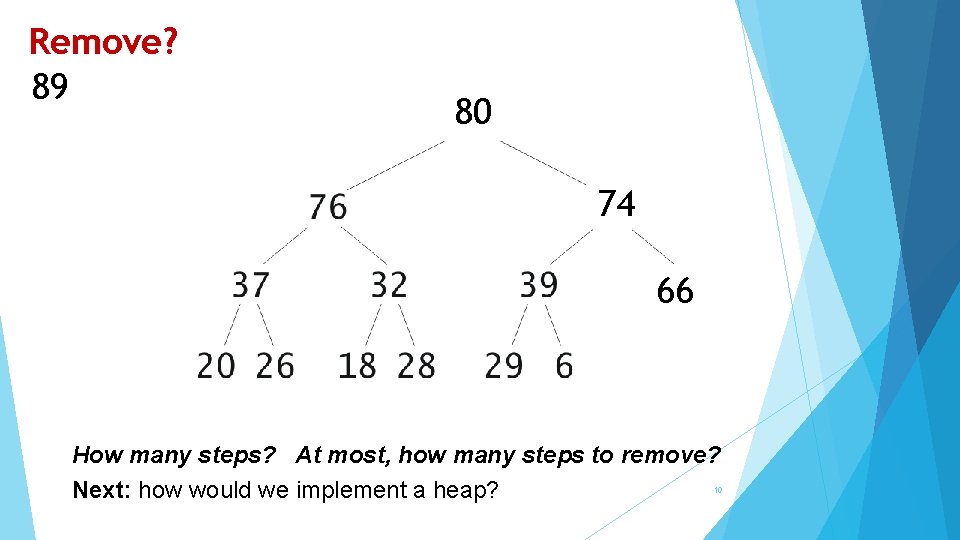
Remove? 89 80 66 66 74 66 How many steps? At most, how many steps to remove? Next: how would we implement a heap? 10

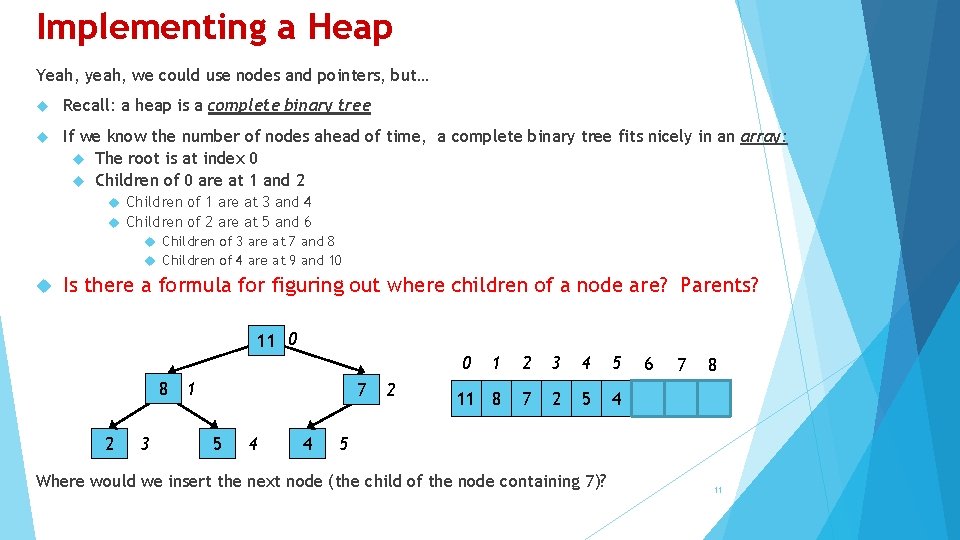
Implementing a Heap Yeah, yeah, we could use nodes and pointers, but… Recall: a heap is a complete binary tree If we know the number of nodes ahead of time, a complete binary tree fits nicely in an array: The root is at index 0 Children of 0 are at 1 and 2 Children of 1 are at 3 and 4 Children of 2 are at 5 and 6 Children of 3 are at 7 and 8 Children of 4 are at 9 and 10 Is there a formula for figuring out where children of a node are? Parents? 11 0 0 8 3 2 3 1 7 5 4 4 2 1 2 3 4 5 11 8 7 2 5 4 6 7 8 5 Where would we insert the next node (the child of the node containing 7)? 11

Inserting into a Heap 1. Insert new item at end; set child to curr_size-1 2. Set parent to (child – 1)/2 3. while (parent ≥ 0 and arr[parent] < arr[child]) 4. Swap arr[parent] and arr[child] 5. Set child equal to parent // so child is now (child – 1)/2 6. Set parent to (child – 1) / 2 How do we delete? 12

Deleting from a Heap 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. Set arr[0] to arr[curr_size-1], and shrink curr_size by 1 Set parent to 0 flag = true while (flag) Set leftchild to 2 * parent + 1, and rightchild to leftchild + 1 if leftchild ≥ curr_size, flag is false else: Set maxchild to leftchild If rightchild < curr_size and arr[rightchild] > arr[leftchild] set maxchild to rightchild If arr[parent] ≥ arr[maxchild], Flag is false else: Swap arr[parent] and arr[maxchild]; set parent to maxchild 13

Performance of Heap A complete tree of height h has: Less than 2 h nodes (why? ) At least 2 h-1 nodes Thus complete tree of n nodes has height O(log n) Insertion and deletion at most are O(log n), always Heap is useful for priority queues 14

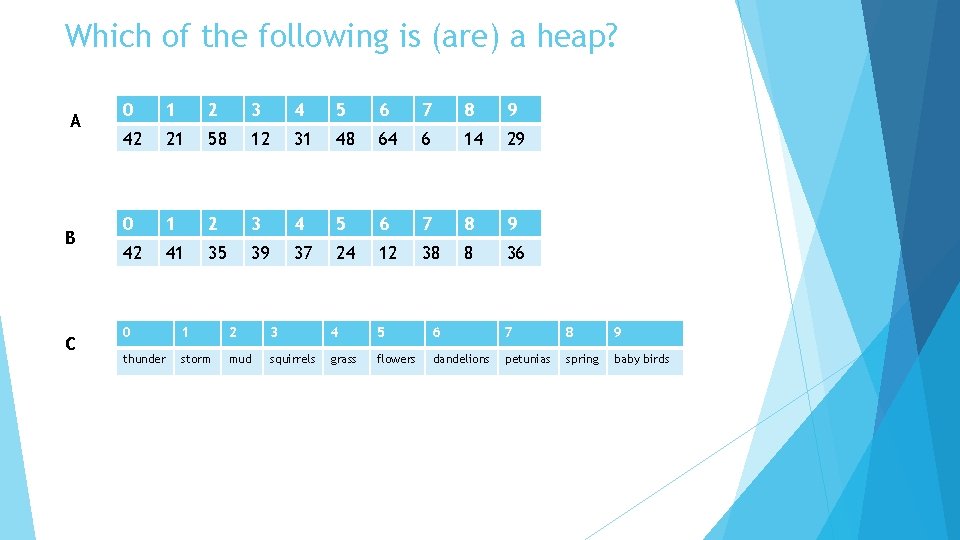
Which of the following is (are) a heap? A B C 0 1 2 3 4 5 6 7 8 9 42 21 58 12 31 48 64 6 14 29 0 1 2 3 4 5 6 7 8 9 42 41 35 39 37 24 12 38 8 36 0 1 2 3 4 5 6 7 8 9 thunder storm mud squirrels grass flowers dandelions petunias spring baby birds

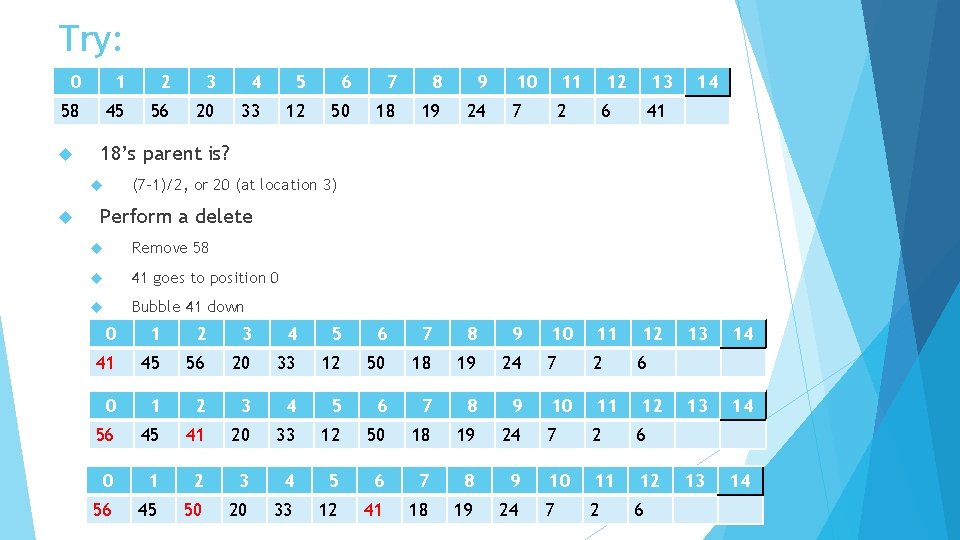
Try: 0 1 2 3 4 5 6 7 8 9 58 45 56 20 33 12 50 18 19 11 12 13 24 7 2 6 41 10 11 12 7 2 6 14 18’s parent is? (7 -1)/2, or 20 (at location 3) 10 Perform a delete Remove 58 41 goes to position 0 Bubble 41 down 0 1 2 3 4 5 6 7 8 9 41 45 56 20 33 12 50 18 19 24 0 1 2 3 4 5 6 7 8 9 56 45 41 20 33 12 50 18 19 24 0 1 2 3 4 5 6 7 8 9 56 45 50 20 33 12 41 18 19 24 13 14

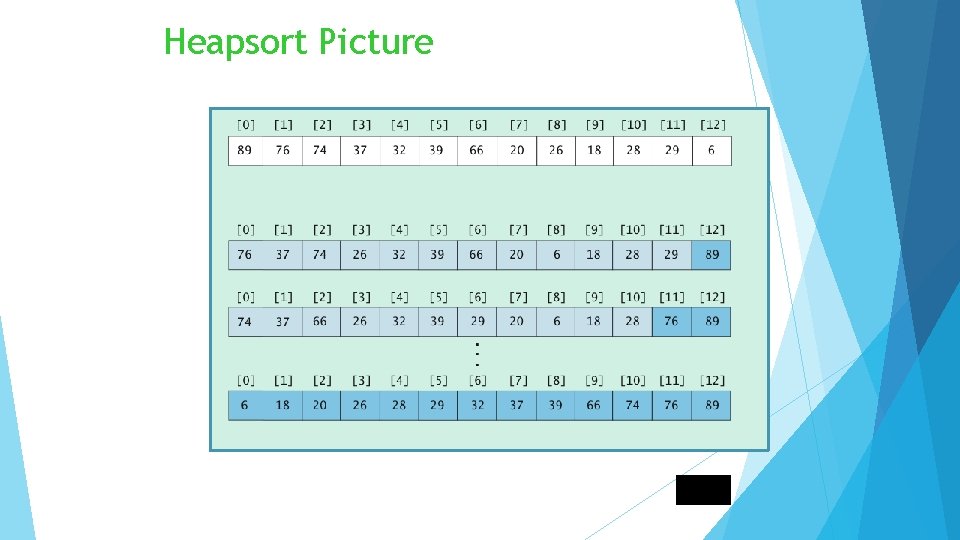
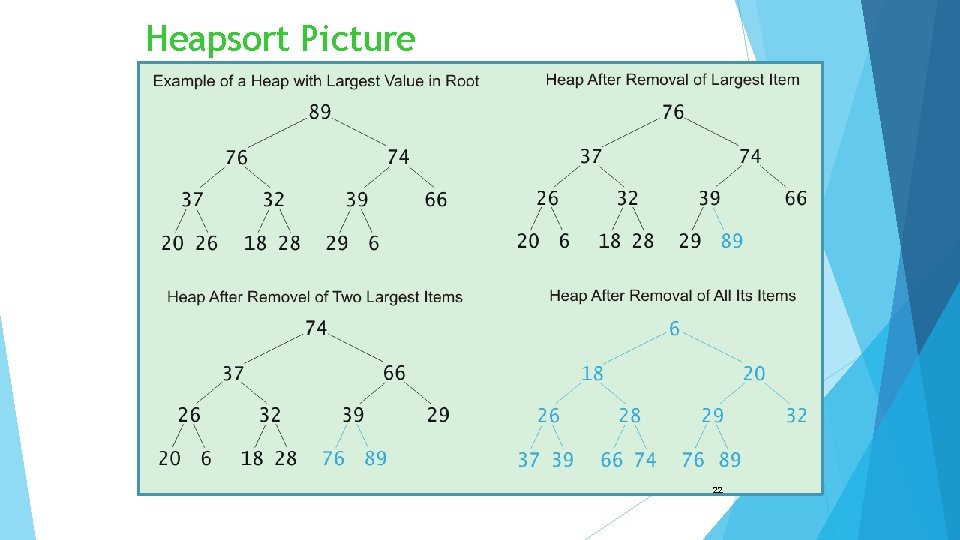
Heapsort Works in place: no additional storage Idea: Insert each element into a priority queue Repeatedly remove from priority queue to array Array slots go from 0 to n-1 18

Heapsort Picture 19

Algorithm for In-Place Heapsort Build heap starting from unsorted array While the heap is not empty Remove the first item from the heap: Swap it with the last item Restore the heap property 20

Heapsort Analysis Insertion cost is log n for heap of size n Removal cost is also log n for heap of size n This is O(n log n) Total removal cost = O(n log n) Total cost is O(n log n) 21

Heapsort Picture 22

Making Heap: Could: Insert each number in a sequence into the heap As you insert, bubble each number up OR: Just insert all numbers into array. Check each node at leaf level with its parent. Make a bunch of tiny heaps Then check each node at height of 2 with its parent Make heaps by switching just max child and parent Continue until you get to root Quicker 26

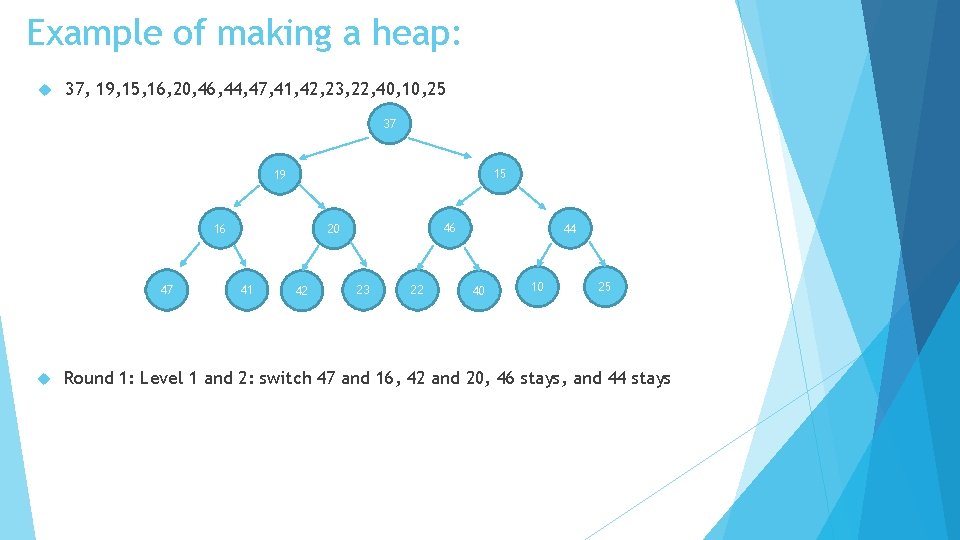
Make a heap (efficiently!): 37, 19, 15, 16, 20, 46, 44, 47, 41, 42, 23, 22, 40, 10, 25

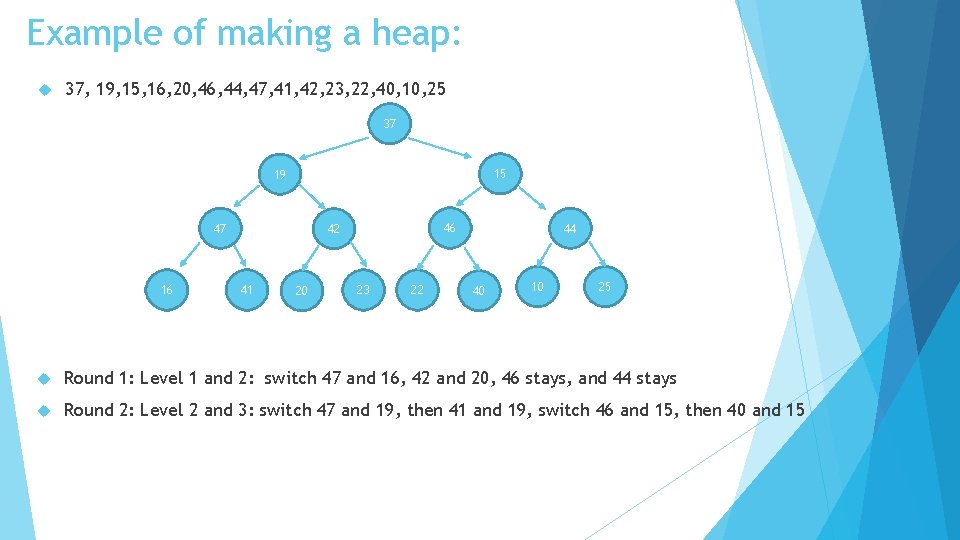
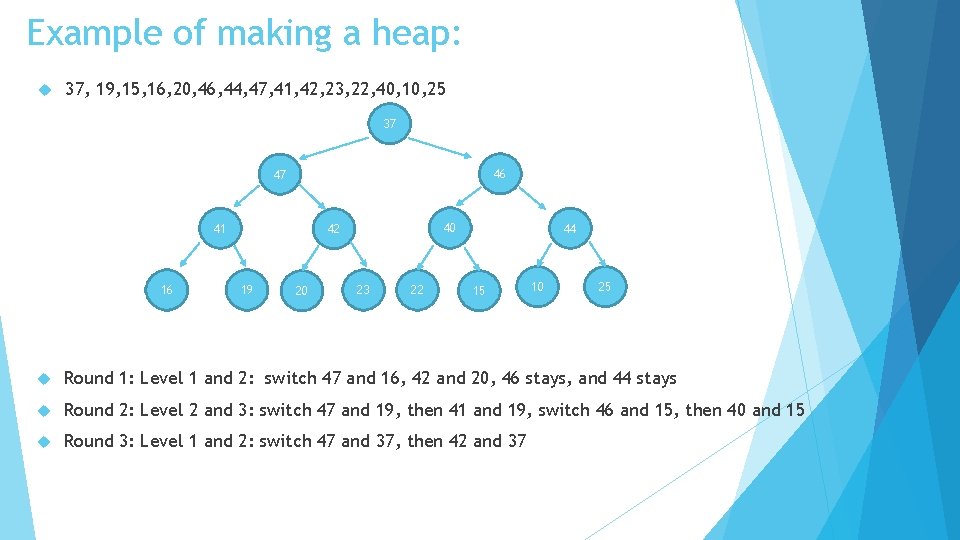
Example of making a heap: 37, 19, 15, 16, 20, 46, 44, 47, 41, 42, 23, 22, 40, 10, 25 37 15 19 16 47 46 20 41 42 23 22 44 40 10 25 Round 1: Level 1 and 2: switch 47 and 16, 42 and 20, 46 stays, and 44 stays

Example of making a heap: 37, 19, 15, 16, 20, 46, 44, 47, 41, 42, 23, 22, 40, 10, 25 37 15 19 47 16 46 42 41 20 23 22 44 40 10 25 Round 1: Level 1 and 2: switch 47 and 16, 42 and 20, 46 stays, and 44 stays Round 2: Level 2 and 3: switch 47 and 19, then 41 and 19, switch 46 and 15, then 40 and 15

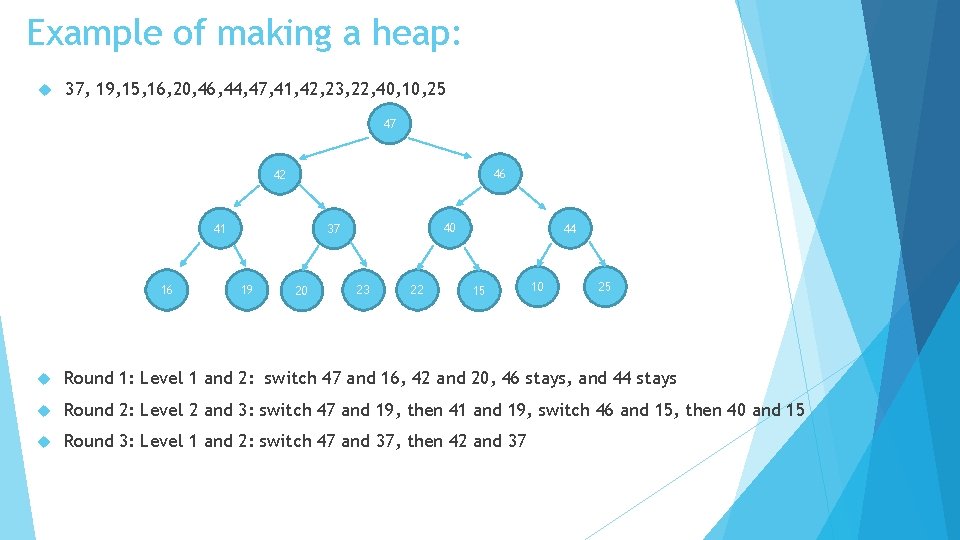
Example of making a heap: 37, 19, 15, 16, 20, 46, 44, 47, 41, 42, 23, 22, 40, 10, 25 37 46 47 41 16 40 42 19 20 23 22 44 15 10 25 Round 1: Level 1 and 2: switch 47 and 16, 42 and 20, 46 stays, and 44 stays Round 2: Level 2 and 3: switch 47 and 19, then 41 and 19, switch 46 and 15, then 40 and 15 Round 3: Level 1 and 2: switch 47 and 37, then 42 and 37

Example of making a heap: 37, 19, 15, 16, 20, 46, 44, 47, 41, 42, 23, 22, 40, 10, 25 47 46 42 41 16 40 37 19 20 23 22 44 15 10 25 Round 1: Level 1 and 2: switch 47 and 16, 42 and 20, 46 stays, and 44 stays Round 2: Level 2 and 3: switch 47 and 19, then 41 and 19, switch 46 and 15, then 40 and 15 Round 3: Level 1 and 2: switch 47 and 37, then 42 and 37

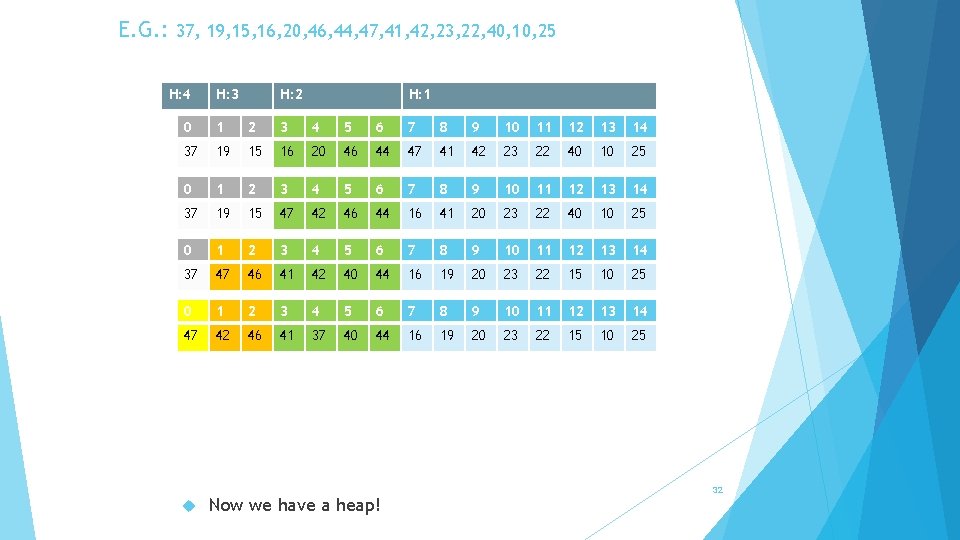
E. G. : 37, 19, 15, 16, 20, 46, 44, 47, 41, 42, 23, 22, 40, 10, 25 H: 4 H: 3 H: 2 H: 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 37 19 15 16 20 46 44 47 41 42 23 22 40 10 25 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 37 19 15 47 42 46 44 16 41 20 23 22 40 10 25 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 37 47 46 41 42 40 44 16 19 20 23 22 15 10 25 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 47 42 46 41 37 40 44 16 19 20 23 22 15 10 25 Now we have a heap! 32

Example: Selection problem (Kth largest) If we had a set of unordered numbers, how would we determine the kth largest (or smallest, by reversing the process)? E. g. , 11, 7, 1, 3, 8, 4, 9, 2, 6, 10, 5 What if we wanted the 5 th smallest (largest) element? How would we do this? How long would it take? 34

Can we do better? Of course. 11, 7, 1, 3, 8, 4, 9, 2, 6, 10, 5 (for this, pretend as if we’re looking for the kth smallest element) 1. build a heap with the array with the smallest value at the top. 2. delete k elements from the heap. Running time? 524 11 8 10 8 13 1 2 3 4 6 11 83 2 5 10 368 11 11 847 10 5 68 10 78 9 8 So 5 is the 5 th smallest element in the list. Can we do better than this? ? 35

Better: 11, 7, 1, 3, 8, 4, 9, 2, 6, 10, 5 1. build a heap (largest elements at top) with just the first k elements. 8 57 426 11 8 724 3 1 742 2. Compare rest of elements with heap. If the new element is smaller than the root, we insert the new element and remove the root. 3. Otherwise we ignore. Note: we are finding the kth smallest element. To find the kth largest element, we would make a heap with the smallest number as the root, and ascend as 36 we move down. Then new elements would be inserted if they were larger than the root.

Analysis: We’re finding the kth smallest in an array of data K must be smaller than n All n elements must at a minimum be compared to the root, In the worst case, must bubble down log k Worst case analysis: n log k