Fast Propositional Algorithms for Planning Fast stochastic algorithms

Fast Propositional Algorithms for Planning • Fast stochastic algorithms for propositional satisfiability: GSAT, WSAT (Walk. SAT) • Compile a planning problem in to a satisfiability problem (example of a constraint satisfaction problem -- CSP), and use a fast algorithm for satisfiability.

Review of Satisfiability • A problem instance is a Boolean conjunctive normal form (CNF) formula, that is, a conjunction of propositional clauses, over some set X 1, …, Xn of propositions. • Goal is to find an assignment to the propositions (variables) that satisfies the CNF formula.

Satisfiability Review (Continued) • Satisfiability is important for several reasons, including – It is at the foundation of NP-completeness – It’s the canonical example of constraint satisfaction problems (CSPs) – Many interesting tasks, including planning tasks, can be encoded as satisfiability problems. • Broadly speaking, CSPs grow easier with

Satisfiability (Continued) • (Continued)… more variables but harder with more constraints. In the case of satisfiability, each clause is a constraint. • Kautz, Levesque, Mitchell, and Selman showed that the critical measure of hardness of satisfiability is the fraction of the number of clauses over the number of variables. For a large fraction, it’s almost always easy

Satisfiability (Continued) • (Continued)… to answer “no” quickly, and for a small fraction it’s almost always easy to answer “yes” quickly. There’s a relatively slim phase transition area in between these extremes where most of the hard problems are located. • GSAT and WSAT were created (by subsets of the preceding authors) to address these.

GSAT • Input: CNF formula and integers Max_flips (e. g. 100) and Max_climbs (e. g. 20). • Output: Yes (satisfiable) or No (couldn’t find a satisfying assignment). Might also output the best assignment found. • Assignments are scored by the number of clauses they satisfy. • GSAT performs a (greedy) hill-climbing search with random restarts (next slide).

GSAT Algorithm • For i from 1 to Max_Climbs: – Randomly draw a truth assignment over the variables in the CNF formula (e. g. flip a coin for each variable to decide whether to make it 0 or 1 -- in practice, use pseudo-random number). If assignment satisfies formula, return “Yes”. – For j from 1 to Max_Flips: • For each variable, calculate the score of the truth assignment that results when we flip the value of

GSAT Algorithm (Continued) • (Continued)… that variable. Make the flip that yields the highest score (need not be greater than or equal to the score of the previous assignment). If the new assignment satisfies the formula, return “Yes”. • Return “No” (no satisfying assignment found, although one might still exist).

Key Points about GSAT • Cannot tell us a formula is unsatisfiable (but we can just run propositional resolution in parallel). • Random re-starts help us find multiple local optima -- the hope is that one will be global. • “Sideways” (or even “downward”) moves help us get off a plateau -- can bounce us off a local optimum. Significant practical advance over standard greedy approach.

Walk. SAT (WSAT) • To further get around the problems of local optima, we can occasionally choose to make a random flip rather than a GSAT flip (as in a random walk). WSAT differs from GSAT as follows: – One additional input: a probability p of a random move at any step. – A random move will involve randomly choosing an unsatisfied clause, randomly …

WSAT (Continued) – (Continued)… choosing a variable in that clause, and flipping that variable in the assignment (even if the net result of the flip is a decrease in score). – For each move, draw a pseudo-random number between 0 and 1. If less than p, make a random move; otherwise, make a GSAT move. • WSAT outperforms GSAT, GAs, and Simulated Annealing on random trials.

Davis-Putnam with RRR • For awhile, GSAT and WSAT displaced the old standard deterministic algorithm, Davis. Putnam. • Actually, what’s called “Davis-Putnam” is really Davis-Putnam-Logemann-Loveland. • Recently, it’s been seen that the key to GSAT/WSAT success is the random restart idea.

DPLL with RRR (Continued) • In the last few years, Davis-Putnam. Logemann-Loveland has been fitted with rapid random restarts (RRR). The result often outperforms WSAT and GSAT. • DPLL is a “backtrack search” algorithm that uses some heuristics. Different restarts involve different choices at backtrack points.

DPLL(CNF formula f) • If f is empty then return yes. • Else if there is an empty clause in f then return no. • Else if there is a pure literal {l} in f then return DPLL(f(l)). • Else if there is a unit clause {l} in f then return DPLL(f(l)). • Else choose a variable v mentioned in f. If DPLL(f(v)) = yes then return yes. Else return DPLL(f(~v)).

DPLL with RRR • Randomly select the variable and variable setting at the choice point. • Restart after a short period of time if a solution has not been found. • Avoids “heavy tail”… directions in the search that will lead to very long run times.

Classical Planning Problem • Input: descriptions of the current world state (initial conditions), the agent’s goal, and the possible actions that can be performed. • Output: a sequence of actions that, when executed from the initial state, will result in a state in which the goal is true.

Formal Language and Vocabulary • Must choose a formal language (e. g. propositional or first-order logic) in which to represent states, goals, and actions. Also need a vocabulary (e. g. choice of propositions or predicate symbols, function symbols, etc. ). • Examples include propositional and first-order STRIPS representations, situation calculus representations, etc.

A Simple Classical Framework • Propositional STRIPS: each action, or operator, characterized by preconditions and postconditions (add list and delete list). • Atomic time: time proceeds in discrete steps. • Omniscient agent: no probabilities on world states, states are completely specified. • Deterministic effects: no probabilities on postconditions.

Classical Framework (Continued) • Conjunctive goals. • Conjunctive preconditions. • Later we will discuss relaxing the constraints of the propositional representation, conjunctive goals, and conjunctive preconditions.

GRAPHPLAN at a High Level • Graph-expansion phase: extend a planning graph forward in time until a necessary (though not sufficient) condition for plan existence has been achieved. • Solution-extraction phase: search the resulting graph for a correct plan. • If no plan is found, then repeat the two phases through more time steps.

Planning Graph • Two types of nodes: propositions and actions. • Nodes partitioned into “levels” labeled 0 to n for some natural number n. • Nodes at even-numbered levels are labeled by propositions, and nodes at odd-numbered levels are labeled by actions.

Planning Graph (Continued) • An odd-numbered level contains one node for each action whose preconditions are present at the previous level, and that level contains no other actions. • An edge exists between a proposition p at level i and an action a at level i+1 if and only if p is a precondition for i.

Planning Graph (Continued) • An action node at level i has an edge to a proposition node at level i+1 if and only if the action has the effect of making the proposition true. • The only other ordinary edges in the graph are as follows: for any proposition p at level i, if p remains true when no action is taken, then there is an edge from p at level i to p at level i+2.

Planning Graph Represents Parallel Actions • A planning graph with k action levels can represent a plan with more than k actions. • That two actions appear at the same level does not imply that both can be executed at once. • Whether two actions can be executed at once is captured by a relation called mutually exclusive (mutex), defined next.

The Mutex Relation • A mutex relation may hold between two actions or two propositions at some level. • Two actions at level i are mutex if either: – the effect of one action is the negation of another action’s effect (inconsistent effects)

Mutex (Continued) – one action deletes the precondition of another (interference) – the actions have preconditions that are mutually exclusive at level i-1 (competing needs)

Mutex Relation (Continued) • Two propositions at level i are mutex if either: – One is the negation of the other – all ways of achieving the propositions (that is, actions at level i-1) are pairwise mutex (inconsistent support).

Mutex Relation (Continued) • Maintenance of a proposition p from propositional level i-1 to propositional level i+1 is also considered as an action at level i (although not represented by a node at level i, but simply an edge from p at level i-1 to p at level i+1. • An action a at level i is mutex with the persistence of p from level i-1 to level i+1 if a makes p false (inconsistent effects).

An Example • Propositions: – garb: garbage is in the house – dinner: dinner is prepared – present: present is wrapped – clean. H: hands are clean – quiet: house is quiet

Example (Continued) • Goal: dinner, present, ~garb • Initial State: garb, clean. H, quiet • Actions: – cook: requires clean. H, achieves dinner – wrap: requires quiet, produces present – carry: achieves ~garb, deletes clean. H – dolly: achieves ~garb, deletes quiet

Example (Continued) • Inferred Mutex relations: – carry and garb are mutex because carry deletes garb. – dolly and wrap are mutex because dolly deletes quiet, which is a precondition for wrap. – At proposition level 2, ~quiet is mutex with present because of inconsistent support.

Solution Extraction • Suppose the goal has n conjuncts. • A plan might exist if GRAPHPLAN has proceeded to some propositional level at which all the goal propositions are present and no pair of these is mutex. (This condition is necessary but not sufficient. ) • Must attempt to extract a solution from the graph---test whether a solution is embedded

Solution Extraction (Continued) • (Continued)… in the graph. • Original method is a backtracking search (depth-first search where state transitions consist of choosing a next action).

Backtrack Algorithm for Solution Extraction • Suppose i is the last level in the planning graph (we assume i is a propositional level). The goal at level i is the goal for the plan. • For each propositional level from i to 0: – For each proposition (say, p) that appears as a conjunct of the goal: • Choose one of the actions a that makes p true (could be a maintenance action) and that is not mutex with any of the actions chosen so far at this level.

Backtracking Solution Extraction Algorithm (Continued) • If no such action exists, backtrack (try another alternative for the previous choice). If no previous choices were made, FAIL. – If the current level i is greater than 0, then take the union of the preconditions for the actions chosen at this level i, and set these to be the conjuncts of the goal for level i-2. Otherwise, return then plan (reverse the order of the sequence of selected actions).

Putting it all Together • The Backtracking Solution Extraction Algorithm succeeds if and only if there exists a plan within the planning graph. • If no plan is found, then extend the planning graph with additional levels.

Example (Continued from Earlier) • There exists no plan in the planning graph to level 2 for our example, because of the mutex relations between the propositions of our goal. • At level 4 several plans exist. Note that the propositions at level 4 are the same as level 2, but there are fewer mutex relations (because we can use maintenance actions for propositions achieved at level 2).

Using Fast Satisfiability Algorithms for Planning • Fast stochastic algorithms for propositional satisfiability: GSAT, WSAT (Walk. SAT) • Compile a planning problem in to a satisfiability problem (example of a constraint satisfaction problem -- CSP), and use a fast algorithm for satisfiability.

SATPLAN • Compile a planning problem into a satisfiability problem. • Use GSAT (or WSAT) to solve the satisfiability problem. A satisfying assignment encodes a plan • We’ll see later that we also can merge GRAPHPLAN and SATPLAN.

SATPLAN (Continued) • As we might expect, we need to encode the initial state, the goal, and the available actions. • Included among the actions are the “maintenance” actions (must write frame axioms). • At the end, we will discuss encoding nonpropositional planning tasks.

A Subtle Point • We still will use the idea of proposition and action levels, but for now we will assume only one action occurs per level. • For now we will consider using SAT-based planning alone, without GRAPHPLAN. • Afterward, we will discuss merging the two.

Compiling Planning to SAT • INIT: initial state is specified by a set of singleliteral (empty-body) clauses. For example, the initial state from our earlier example would be specified by the clauses garb-0, clean. H-0, quiet-0, ~dinner-0, and ~present-0. • GOAL: To test for a plan of length at most n, each goal conjunct is asserted to be true at level 2 n. For the goal in our example, we

Compilation (Continued) • (Continued)… if we want to test whether it is true at time 1, we would add the following single-literal (empty-body) clauses: ~garb-2, dinner-2, and present-2. • ACTIONS: Actions imply both their preconditions and effects. Thus among the clauses we would add for our preceding example would be (~cook-1 | clean. H-0) as

Compiling (Continued) • (Continued)… well as (~cook-1 | clean. H-0). • EXCLUSION: axioms saying at most one action occurs at an action level (can relax): for all actions a and b add (~a-i | ~b-i). • FRAME: Also must encode some type of frame axioms (maintenance actions). We’ll spend several slides on this because it is more complicated and two options exist.

Two Types of Frame Encodings • Classical frame axioms + at-least-one axioms: classical frame axioms say which propositions are left unchanged by a given action, and at-least-one axioms enforce that some action occurs at each action level. • Explanatory frame axioms: enumerate the set of actions that could have occurred to account for some state change.

Classical Frame Axioms • In our previous example, we would specify that if the garbage was in the house at level 0, and our action at level 1 was cook, then garbage is still in the house at level 2: (~garb-0 | ~cook-1 | garb-2). • In general, for each action a and each proposition p that a leaves unchanged, we have (~p-(i-1) | ~a-i | p-(i+1)).

At-Least-One Axioms • But if no action occurs at an action level, we will lose all our propositions from the previous level. Therefore, we add axioms that specify an action must occur at each level. • For each action level i, we have a disjunction of all possible actions, e. g. , (cook-i | wrap-i | dolly-i | carry-i).

Explanatory Frame Axioms • If garbage was in the house at level 0 but is not in the house at level 2, then one of the actions that removes garbage must have occurred at level 1: (~garb-0 | garb-2 | carry-1 | dolly-1). • We do not need at-least-one axioms, but we do still need exclusion axioms.

Linking GRAPHPLAN and SATPLAN • Build the planning graph as normally, and then convert the planning graph (partially solved and hence simpler task) into a CNF formula. • INIT and GOAL axioms are as before. • Actions imply their preconditions (we use our ACTION axioms without the implication of effects.

Linking (Continued) • (Almost) explanatory frame axioms: each fact at a propositional level implies the disjunction of all actions that could have caused it, including explicit maintenance actions. For example, if garbage is not in the house at level 4, then either dolly or carry occurred at level 3 or we maintained garbage from level 2: . . .

Linking (Continued) • Specialized exclusion axioms: instead of saying no two actions can occur at the same action level, we simply say that conflicting (mutex) actions cannot occur at the same level. • GSAT or WSAT can the be used to more efficiently search the planning graph (so represented) for a plan.

Relaxing the Restriction to Propositional Logic • Suppose we have a first-order representations, such as the standard STRIPS representation for the blocks world. • Neither GRAPHPLAN nor SATPLAN (nor their combination) as described so far can be applied, because they assume a propositional representation. • Solution: convert to propositional.

Methods of Conversion • Convert each ground atom (member of the Herbrand Universe) and level pair to a distinct proposition. For example, each of the following becomes a proposition: – ontop(a, b) at level 0 – ontop(b, a) at level 0 – clear(b) at level 0

Conversion (Continued) – ontop(a, b) at level 2 – unstack(a, b) at level 1 – unstack(b, a) at level 1 – stack(a, b) at level 1 – pickup(a) at level 1 – etc.

Conversion (Continued) • The problem with the preceding method is that the number of propositions grows exponentially with the predicate arity. • Alternative: Break the representation of each first-order ground atom into parts (e. g. , arguments or bits), all of which have to be true for the atom to be construed as true. – One distinct proposition for each argument of

Conversion (Continued) – (Continued)… of each ground atom. – One distinct proposition for each argument of a given predicate (some ground atoms could share some propositions). – Number all the ground atoms, and have one proposition for each bit in the binary representation of the atom’s number.

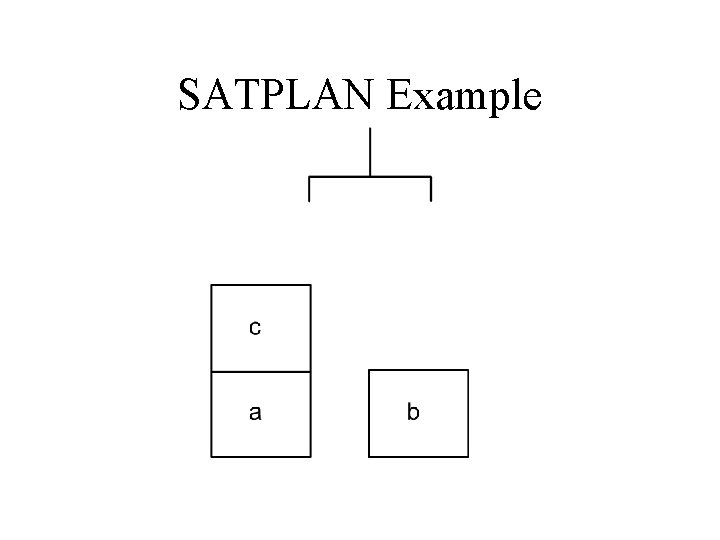
SATPLAN Example

Example Conversion • INIT: – x 1: ontable(a, 0) – x 2: ontable(b, 0) – x 3: ontop(c, a, 0) – x 4: clear(c, 0) – x 5: clear(b, 0) – x 6: handempty(0)

Example (Continued) • GOAL: – x 7: clear(a, 2) – x 8: clear(c, 2)

Example (Continued) • ACTIONS: – pickup(a, 1) -> ontable(a, 0) & clear(a, 0) & handempty(0) • • Must convert into clauses: ~pickup(a, 1) | ontable(a, 0) ~pickup(a, 1) | clear(a, 0) ~pickup(a, 1) | handempty(0) – Similarly for pickup(b, 1) and pickup(c, 1)

Example (Continued) • ACTIONS (Continued): – putdown(a, 1) -> holding(a, 0) • Must convert into clauses: • ~putdown(a, 1) | holding(a, 0) – Similarly for putdown(b, 1) and putdown(c, 1)

Example (Continued) • ACTIONS (Continued): – stack(a, b, 1) -> clear(b, 0) & holding(a, 0) • Must convert into clauses: • ~stack(a, b, 1) | clear(b, 0) • ~stack(a, b, 1) | holding(a, 0) – Similarly for other instantiations of the stack operator and for other action levels.

Example (Continued) • ACTIONS (Continued): – unstack(a, b, 1) -> ontop(a, b, 0) & handempty(0) & clear(a, 0) • • Must convert into clauses: ~unstack(a, b, 1) | ontop(a, b, 0) ~unstack(a, b, 1) | handempty(0) ~unstack(a, b, 1) | clear(a, 0) – Similarly for other instantiations of the unstack operator and for other action levels.

Example (Continued) • FRAME AXIOMS (Explanatory): – ~clear(a, 0) & clear(a, 2) -> • unstack(b, a, 1) | • unstack(c, a, 1) | • putdown(c, 1). – Convert to clauses by generalization of the rule (a&b) | (c&d) = (a|c)&(a|d)&(b|c)&(b|d). Must build frame axioms for all action instances. – Also need clear(a, 0) & ~clear(a, 2) ->. . .

Example (Continued) • FRAME AXIOMS (Explanatory): – clear(a, 0) & ~clear(a, 2) -> • stack(b, a, 1) | • stack(c, a, 1) | • pickup(c, 1). – Must repeat these for all other time steps, and must also do explanatory frame axioms for all other propositions besides those based on clear.

Example (Continued) • EXCLUSION AXIOMS: For each pair of action instances a and b and each action level i, add (~a-i | ~b-i). • For example, we would add (among others): – ~stack(a, b, 1) | ~pickup(c, 1) – ~unstack(a, b, 1) | ~unstack(b, a, 1) – etc.

Example of the Benefit of Action Splitting • With just 10 blocks, we will require nearly 10, 000 axioms of the form ~stack(a, b, 1) | ~stack(c, d, 1). To see this, note that 90 ground stack literals can be built given 10 blocks, and therefore 90*89 pairs of stack literals can be built. • With splitting instead, we require only 180 literals (10*9 for the first argument, and 10*9 for the second).

SATPLAN • Compile a planning problem into a propositional satisfiability problem. • Use a fast satisfiability algorithm to solve the satisfiability problem. A satisfying assignment encodes a plan • We’ll see later that we also can merge GRAPHPLAN and SATPLAN.

SATPLAN (Continued) • As we might expect, we need to encode the initial state, the goal, and the available actions. • Included among the actions are the “maintenance” actions (must write frame axioms). • At the end, we will discuss encoding nonpropositional planning tasks.

A Subtle Point • We still will use the idea of proposition and action levels, but for now we will assume only one action occurs per level. • For now we will consider using SAT-based planning alone, without GRAPHPLAN. • Afterward, we will discuss merging the two.

Compiling Planning to SAT • INIT: initial state is specified by a set of single-literal (empty-body) clauses. For example, the initial state from our earlier example would be specified by the clauses garb-0, clean. H-0, quiet-0, ~dinner-0, and ~present-0. • GOAL: To test for a plan of length at most n, each goal conjunct is asserted to be true at level 2 n. For the goal in our example, we

Compilation (Continued) • (Continued)… if we want to test whether it is true at time 1, we would add the following single-literal (empty-body) clauses: ~garb-2, dinner-2, and present-2. • ACTIONS: Actions imply both their preconditions and effects. Thus among the clauses we would add for our preceding example would be (~cook-1 | clean. H-0) as

Compiling (Continued) • (Continued)… well as (~cook-1 | clean. H-0). • EXCLUSION: axioms saying at most one action occurs at an action level (can relax): for all actions a and b add (~a-i | ~b-i). • FRAME: Also must encode some type of frame axioms (maintenance actions). We’ll spend several slides on this because it is more complicated and two options exist.

Two Types of Frame Encodings • Classical frame axioms + at-least-one axioms: classical frame axioms say which propositions are left unchanged by a given action, and at-least-one axioms enforce that some action occurs at each action level. • Explanatory frame axioms: enumerate the set of actions that could have occurred to account for some state change.

Classical Frame Axioms • In our previous example, we would specify that if the garbage was in the house at level 0, and our action at level 1 was cook, then garbage is still in the house at level 2: (~garb-0 | ~cook-1 | garb-2). • In general, for each action a and each proposition p that a leaves unchanged, we have (~p-(i-1) | ~a-i | p-(i+1)).

At-Least-One Axioms • But if no action occurs at an action level, we will lose all our propositions from the previous level. Therefore, we add axioms that specify an action must occur at each level. • For each action level i, we have a disjunction of all possible actions, e. g. , (cook-i | wrap-i | dolly-i | carry-i).

Explanatory Frame Axioms • If garbage was in the house at level 0 but is not in the house at level 2, then one of the actions that removes garbage must have occurred at level 1: (~garb-0 | garb-2 | carry-1 | dolly-1). • We do not need at-least-one axioms, but we do still need exclusion axioms.

Linking GRAPHPLAN and SATPLAN • Build the planning graph as normally, and then convert the planning graph (partially solved and hence simpler task) into a CNF formula. • INIT and GOAL axioms are as before. • Actions imply their preconditions (we use our ACTION axioms without the implication of effects.

Linking (Continued) • (Almost) explanatory frame axioms: each fact at a propositional level implies the disjunction of all actions that could have caused it, including explicit maintenance actions. For example, if garbage is not in the house at level 4, then either dolly or carry occurred at level 3 or we maintained garbage from level 2: . . .

Linking (Continued) • Specialized exclusion axioms: instead of saying no two actions can occur at the same action level, we simply say that conflicting (mutex) actions cannot occur at the same level. • GSAT or WSAT can the be used to more efficiently search the planning graph (so represented) for a plan.

Relaxing the Restriction to Propositional Logic • Suppose we have a first-order representations, such as the standard STRIPS representation for the blocks world. • Neither GRAPHPLAN nor SATPLAN (nor their combination) as described so far can be applied, because they assume a propositional representation. • Solution: convert to propositional.

Methods of Conversion • Convert each ground atom (member of the Herbrand Universe) and level pair to a distinct proposition. For example, each of the following becomes a proposition: – ontop(a, b) at level 0 – ontop(b, a) at level 0 – clear(b) at level 0

Conversion (Continued) – ontop(a, b) at level 2 – unstack(a, b) at level 1 – unstack(b, a) at level 1 – stack(a, b) at level 1 – pickup(a) at level 1 – etc.

Conversion (Continued) • The problem with the preceding method is that the number of propositions grows exponentially with the predicate arity. • Alternative: Break the representation of each first-order ground atom into parts (e. g. , arguments or bits), all of which have to be true for the atom to be construed as true. – One distinct proposition for each argument of

Conversion (Continued) – (Continued)… of each ground atom. – One distinct proposition for each argument of a given predicate (some ground atoms could share some propositions). – Number all the ground atoms, and have one proposition for each bit in the binary representation of the atom’s number.