Introduction to Logic 3 lecture Propositional Logic Continuing


![Normal forms of formulas (p q) [(p q) (q p)] [( p q) ( Normal forms of formulas (p q) [(p q) (q p)] [( p q) (](https://slidetodoc.com/presentation_image_h/c06824ded8c80a66a12473ede7abe109/image-3.jpg)






























- Slides: 37

Introduction to Logic 3. lecture Propositional Logic Continuing Marie Duží Introduction to Logic 1

Normal forms of formulas of propositional logic • To each formula of propositional logic there is just one truth-value function, i. e. , mapping {p, q, r…} {0, 1} (the truth-value table). • On the other hand, to each such function there are infinitely many formulas, which are mutually equivalent. • Definition: Formulas A, B are equivalent, notation A B, if A, B have exactly the same models, i. e. , A and B express the same truth-value function. In other words, A entails B, and vice versa: A B iff A |= B a B |= A. • Example: p q (p q) (p p) . . . • Note: Do not confuse the equivalence of formulas A B (‘ ‘ is a sign of meta-language!) with a formula of the form A B. However, it holds that A B if and only if the formula |= A B (is a tautology). • Example: (p q) [(p q) (q p)] iff • |= [(p q) (q p))] Introduction to Logic 2
![Normal forms of formulas p q p q q p p q Normal forms of formulas (p q) [(p q) (q p)] [( p q) (](https://slidetodoc.com/presentation_image_h/c06824ded8c80a66a12473ede7abe109/image-3.jpg)
Normal forms of formulas (p q) [(p q) (q p)] [( p q) ( q p)] [(p q) ( p q)] …. • It is useful to determine a normal (standardized) form of a formula: to select one (or two) determined forms out of these infinitely many equivalent forms. • The class of equivalent formulas is then represented by the chosen formula in the normal form. • In the above example the second and third formulas are in a normal form. • Introduction to Logic 3

Normal forms (of PL formulas): definition Literal is a proposition symbol or its negation: Ex. : p, q, r, . . . Elementary conjunction (EC) is a conjunction of literals. Ex. : p q, r r, . . . Elementary disjunction (ED) is a disjunction of literals. Ex. : p q, r r, . . . Complete elementary conjunction (CEC) of a given set S of elementary propositional symbols is an elementary conjunction in which each symbol (element of S) occurs just once: Ex. : p q Complete elementary disjunction (CED) of a given set S of elementary propositional symbols is an elementary disjunction in which each symbol (element of S) occurs just once: Ex. : p q Disjunctive normal form (DNF) of a formula F is a formula F’ such that F’ is equivalent to F and F’ has the form of a disjunction of elementary conjunctions. Example: DNF(p p): (p p) ( p p), p p Conjunctive normal form (CNF) of a formula F is a formula F’ such that F’ is equivalent to F and F’ has the form of a conjunction of elementary disjunctions. CNF(p p): ( p p) Complete disjunctive normal form (CDNF) of a formula F is a formula F’ equivalent to F such that F’ has the form of a disjunction of complete elementary conjunctions. UDNF(p q): (p q) ( p q) Complete conjunctive normal form (CCNF) of a formula F is a formula F’ equivalent to F such that F’ has the form of a conjunction of complete elementary disjunctions. UKNF(p q): ( p q) ( q p) 4 CDNF and CCNF are called canonic (or standard) forms of a formula.

Normal forms of PL formulas How to find canonic forms (i. e. , CDNF, CCNF) of a formula? CDNF: disjunction = 1, if at least one CEC = 1, i. e. , all the literals in this CEC = 1. CCNF: conjunction = 0, if at least one CED = 0, i. e. , all the literals in this CED = 0. Therefore: CDNF (CCNF) can be constructed from the truth-table in such a way, that we take into account only rows with the value 1 (0) and ensure “the correct value of literals” – 1 (0). Introduction to Logic 5

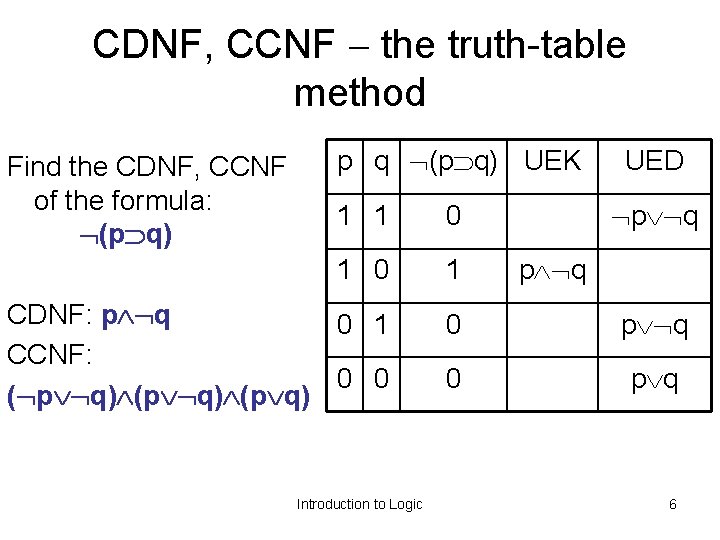
CDNF, CCNF the truth-table method Find the CDNF, CCNF of the formula: (p q) p q (p q) UEK UED p q 1 1 0 1 CDNF: p q 0 1 CCNF: 0 0 ( p q) (p q) 0 p q Introduction to Logic p q 6

CDNF, CCNF by equivalent transforming method: p q (p q) CCNF [p (q q ] [ q (p p ] p q CDNF Note: In the second line we make use of the fact that a disjunction of any formula A with a contradiction F is equivalent to A: A F A In the third line we make use of distributive laws Statement: Each formula which is not a contradiction has a CDNF, and each formula which is not a tautology has a CCNF Introduction to Logic 7

Reverse task: given a CDNF, CCNF, find a simpler original formula; Example • An alchemist is imprisoned. He received 5 messages with the following content: – p: – q: – r: You will succeed in converting lead to gold. On April 1 st your brother-in-law will become an attorney. After April 1 st you may expect pleading. 1 st message says: p q r 2 nd message says: p q r 3 rd message says: p q r 4 th message says: p q r 5 th message: At least one of the previous messages is true. – Question: What did the poor alchemist learn? • Solution: (p q r) ( p q r). Hence we need to find a formula F which has the above CDNF. By means of distribute laws we obtain: (p q r) (p q) (r r) (p q) (p q) • Answer: You will succeed in converting lead to gold if and only if on April 1 st your brother-in-law becomes an attorney. Introduction to Logic 8

Question: how many binary truth-value functions (hence how many binary connectives) are there? X Y 0 1 2 3 4 5 6 7 8 9 1 1 1 0 1 2 3 4 5 1 1 0 1 0 1 1 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1 0 0 0 0 0 1 1 1 1

Which is the minimal number of truthfunctional connectives? • According to the Statement on normal forms (see slide 7) the following connectives suffice: , , (funkcionally complete system) The following systems of truth-functional connectives are functionally complete: 1. { , , }, 2. { , } or { , }, 3. { , }, 4. { } or { }. Hence in order to express any truth-value function (and thus any PL formula) just one connective suffices! Either Scheffer’s NAND or Pierce’s NOR Introduction to Logic 10

Proof on the minimum of connectives • • The system { , , } is sufficient according to the Statement on normal forms Transition to the system { , } or { , }: A B ( A B), A B ( A B) Transition to the system { , }: A B, A B (A B) Transition to the system { } or { }: A A A, A B (A B), ( is NAND), A A A, A B (A B), ( is NOR). Introduction to Logic 11

A method of creating DNF, CNF: semantic tableau • Disjunctive tableau: a tree where branching means disjunction and leaves are conjunctions of literals • Conjunctive tableau: a tree where branching means conjunction and leaves are disjunctions of literals • |= A (tautology) all the leaves of the conjunctive tableau have to be closed, i. e. , contain an opposite pair of literals: p, because (p p) – tautology • A |= (contradiction) all the leaves of the disjunctive tableau have to be closed, i. e. , contain an opposite pair of literals: p, because (p p) – contradiction Introduction to Logic 12

Way of creating a tableau 1. A formula is transformed in such an equivalent way that the negation is moved inside (to elementary symbols). 2. Formulas of an implicative or equivalence form are transformed by means of: (p q) ( p q), (p q) ( q p) (p q) ( p q) 3. Construct the tableau by applying a distributive law where-ever necessary. Introduction to Logic 13

Applying a distributive law: disjunctive tableau • • • (Branching means disjunction, comma conjunction. ) Repeat: (from left to right) branch the formula into a left -hand part and a right-hand part whenever you find a disjunction. The left-hand branch contains the left disjunct + the rest of formula where instead of conjunction there is a comma. The right-hand part contains the right disjunct + the rest of formula where instead of conjunction there is a comma. Until: there is no disjunction in any branch and the tree contains in its leaves only literals separated by commas, i. e. , elementary conjunctions. Introduction to Logic 14

Applying a distributive law: conjunctive tableau • • (dual to disjunctive) (Branching means conjunction, comma disjunction. ) Repeat: (from left to right) branch the formula into a left -hand part and a right-hand part whenever you find a conjunction. The left-hand branch contains the left conjunct + the rest of formula where instead of conjunction there is a comma. The right-hand part contains the right conjunct + the rest of formula where instead of disjunction there is a comma. Until: there is no conjunction in any branch and the tree contains in its leaves only literals separated by commas, i. e. , elementary disjunctions. Introduction to Logic 15

Prove that a formula is a a) tautology, b) contradiction a) Proof that a formula F is a contradiction: Construct the disjunctive tableau. If all the branches are closed, i. e. , each leave of the tree contains a couple of opposite literals (e. g. p, which means p p), the formula F is a contradiction. b) Proof that a formula F is a tautology: Construct the conjunctive tableau. If all the branches are closed, i. e. , each leave of the tree contains a couple of opposite literals (e. g. p, which means p p), the formula F is a tautology. Example (next slide): proof of a contradiction. 16

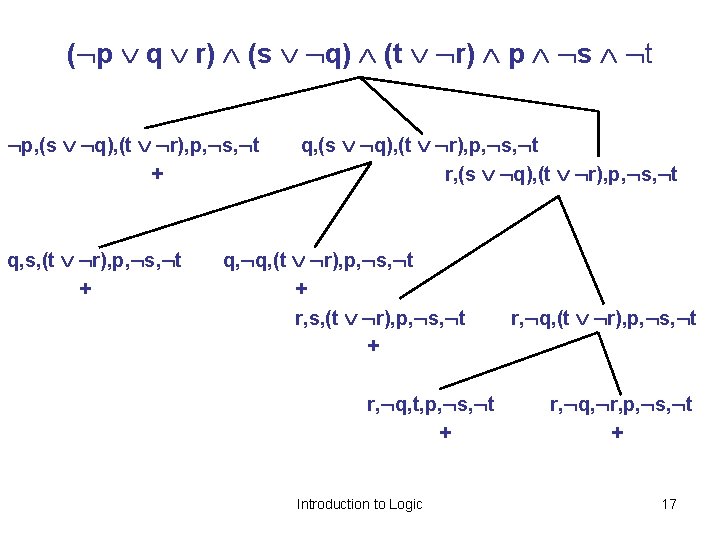
( p q r) (s q) (t r) p s t p, (s q), (t r), p, s, t + q, s, (t r), p, s, t + q, (s q), (t r), p, s, t r, (s q), (t r), p, s, t q, q, (t r), p, s, t + r, s, (t r), p, s, t + r, q, t, p, s, t + Introduction to Logic r, q, (t r), p, s, t r, q, r, p, s, t + 17

Find consequences of a formula • • Complete a disjunctive semantic tableau which is not closed in each branch by such a set of literals that closes all the branches. Negation of the conjunction of added literals is entailed. For instance, if you add p, q, then you added the formula p q, hence p q, i. e. p q is entailed. By a dual way you may use a conjunctive normal form. Introduction to Logic 18

Complete normal forms Looking at a tableau, you can easily see why • a tautology does not have a complete conjunctive normal form (CCNF) and why • a contradiction does not have a complete disjunctive normal form (CDNF): If a formula is a tautoloy, then all the branches of a conjunctive tableau are closed, i. e. , in each ED there is a couple of opposite literals p, which means p p. but then the elementary disjunction is not complete. Hence the CCNF of the formula does not exist. • Similarly for CDNF. Introduction to Logic 19

CDNF of a tautology with one (T 1), two (T 2), three (T 3) variables T 1 p p T 2 (p q) ( p q) T 3 (p q r) ( p q r) For each valuation v there has to be at least one CEC true. Introduction to Logic 20

If a formula is not a tautology, at least one of these CECs has to be missing in the respective CDNF. Therefore, if we construe a CDNF from a truth table, we take into account only those rows, where the function has the value 1 (value False – 0 does not matter, because A F A) and construe CEC in such a way that the CEC is true. Similarly for CCNF – take into account 0 -s. Introduction to Logic 21

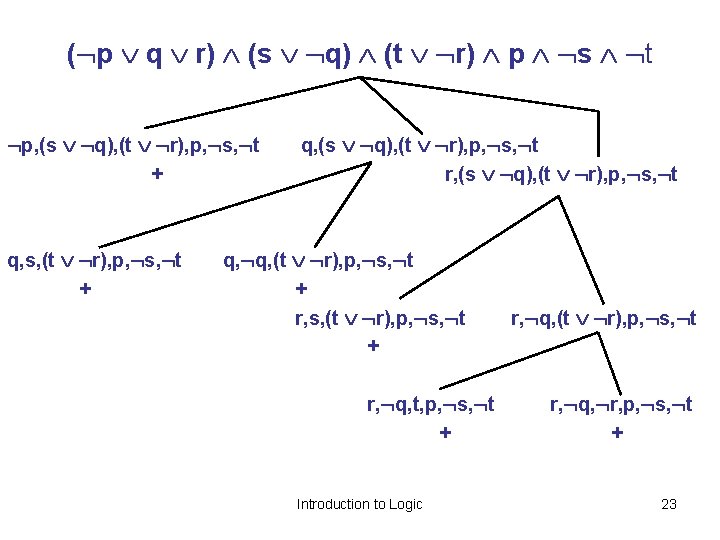
Prove that the following formula F is a tautology: F: [(p (q r)) ( s q) (t r)] (p (s t)) • Indirect proof. By means of the disjunctive normal form prove that the formula F is a contradiction: (p (q r)) ( s q) (t r) p s t ( p q r) (s q) (t r) p s t Construing a disjunctive tableau (branching – disjunction, comma – conjunction): Introduction to Logic 22

( p q r) (s q) (t r) p s t p, (s q), (t r), p, s, t + q, s, (t r), p, s, t + q, (s q), (t r), p, s, t r, (s q), (t r), p, s, t q, q, (t r), p, s, t + r, s, (t r), p, s, t + r, q, t, p, s, t + Introduction to Logic r, q, (t r), p, s, t r, q, r, p, s, t + 23

What is logically entailed by the formula G ? G: (p (q r)) ( s q) (t r) Solution: When you make a semantic tableau of G, you will see that the following literals are missing in all the branches: p, s, t. Hence the tableau of the formula (G p s t) is closed. The formula (G p s t) is a contradiction. Hence: |= G (p s t). G |= (p s t), G |= (p (s t)) No wonder, because the formula F is a tautology ! Hence: Introduction to Logic 24

Prove that the formula F is a tautology: [(p (q r)) ( s q) (t r)] (p (s t)) • Direct proof: by means if the conjunctive normal form prove that |= F: • branching – conjunction, comma – disjunction F (p q r) ( s q) ( t r) p s t And so on, similarly (in a dual way) to the indirect proof. Introduction to Logic 25

Rezolution method in propositional logic n n n From a practical point of view a semantic tableau is not favourable If you want to prove that P 1, . . . , Pn |= Z, it is sufficient to prove that |= (P 1 . . . Pn) Z, i. e. , P 1 . . . Pn Z is a contradiction. But, to prove it by the tableau method, you need the disjunctive normal form. Which means that you have to transform the formula that is (almost) in the conjunctive form into the disjunctive form, which yields a lot of applications of the distributive law. Using a tableau often yields a lot distributive steps It is easier to directly prove the contradiction, i. e. , that the formula P 1 . . . Pn Z is not satisfiable.

Resolution rule in the propositional logic Let l be a literal. From (A l) (B l) infer (A B). Notation: (A l) (B l) –––––––– (A B) resolvent This rule does not lead to an equivalent formula. But it preserves satisfiability. Proof: Let formula (A l) (B l) be non-contradictory. hence there is a valuation v in which it is true. But then in this v both the disjuncts (so called clauses) are true: (A l) and (B l). Let v(l) = 0. Then w(A) = 1 and w(A B) = 1. Let v(l) = 1. Then w( l) = 0 and w(B) = 1, a thus w(A B) = 1. In both cases the formula A B is true in the model v of the opriginal formula, hence it is not a contradiction. Introduction to Logic 27

Proof by resolution in PL If you realise that the above proof is valid for any valuation v, then you see that the rule is truth preserving: (A l) (B l) |= (A B). n Thus you obtained also a method of finding logical consequences of a formula. n Moreover: (A l) (B l) (A B) Introduction to Logic 28

Clausal form n The conjunctive normal form is called clausal form. Particular conjuncts (i. e. , elementary disjunctions) are called clauses. n Example: Transition of a formula into the clausal form: [((p q) (r q) r) p] ((p q) (r q) r) p ( p q) (r q) r p n The formula consists of four clauses. The proof of contradiction: n ( p q) (r q) ( p r) r p p Introduction to Logic 29

Proof by resolution • R(F) – conjunctive extension of a formula F by all its resolvents • R 0(F) = F, Ri(F) = R(Ri-1(F)) – rezolution closure of F. It holds that Ri(F) F • Proof: A is a contradiction (not satisfiable): there is an n such that Rn(A) contains the empty clause: • Proof: A is a tautology: A is a contradiction • Proof: a set of formulas {A 1, …, An} is not satisfiable. We prove that the formula A 1 . . . An is a contradiction • Infer logical consequences of {A 1, …, An}: infer all the resolvents • Proof of validity: A 1, …, An |= Z – Direct: by step-by-step inferring resolvents from A 1, …, An you obtain Z – Indirect: prove that A 1 . . . An Z is a tautology, i. e. , A 1 . . . An Z is a contradiction, i. e. , the set {A 1, . . . , An, , Z} is not satisfiable Introduction to Logic 30

Examples • • Particular clauses are numbered. gradually infer resolvents (that logically follow from the clauses). When performing an indirect proof, you have to infer p p, the empty clause Prove that the following f. is a contradiction: ( q p) (p r) (q r) p 1. q p 2. p r 3. q r 4. p 5. p r rezolution: 1, 3 6. p rezolution: 2, 5 7. 4, 6 Question: What follows from the formula ( q p) (p r) (q r) ? Answer: the formula p 31

Examples • 1. 2. 3. 4. 5. 6. Direct proof: p q r, s q, t r |= p (s t) p q r s q t r p s r rezolution 1, 2 p s t rezolution 3, 4 p s t p (s t) QED Introduction to Logic 32

Examples • Indirect proof: p q r, s q, t r |= p (s t) 1. p q r 2. s q 3. t r 4. p s r rezolution 1, 2 5. p s t rezolution 3, 4 6. p nega 7. s ted 8. t conclusion 9. p s t, p, s, t |= s t, s, t |= t, t |= Introduction to Logic 33

Logic programming Strategies of generating resolvents: • Breadth-first (pursue all closest paths first) – Resolution closure – generates all resolvents – It can be rather inefficient due to combinatorial explosion of resolvents • Depth-first (top down: pursue first path to exhaustion before looking an next path) – It is very simple and efficient to implement, but it is not complete; it can lead to some very odd infinite loops though there is a solution in a neighbouring branch. Introduction to Logic 34

Example: incompleteness of the depth-first strategy • • 1. 2. 3. 4. 5. 6. d e (b a) (e b) (d a) |= a (? ) Logic program (depth-first, top down strategy; goal driven): D. fact E. fact A : B. rule (A, if B) B : E. rule (B, if E) A : D. rule (A, if D) ? A query, goal – the program tries to meet the goal A by searching top down; the clause 3 meets the goal generates a new goal B. Succeeds with the clause 4 a new goal E – met by the clause 2. – Yes ; - or generates backtracking: again ? A – clause 5 – goal D – clause 1. - Yes Introduction to Logic 35

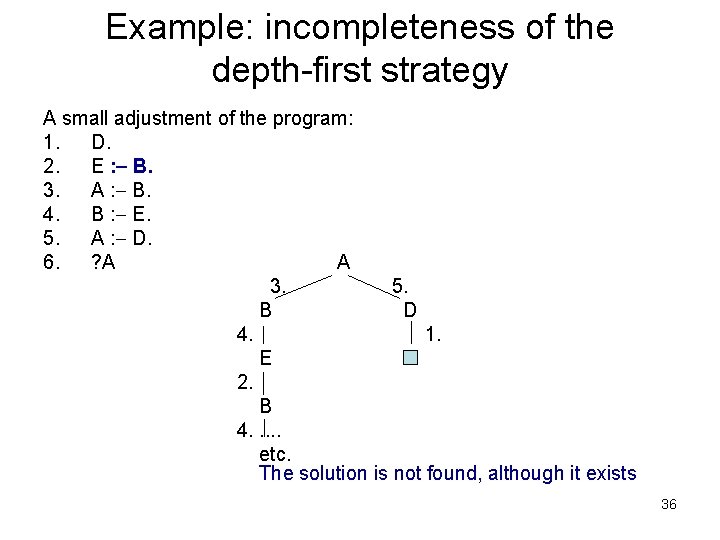
Example: incompleteness of the depth-first strategy A small adjustment of the program: 1. D. 2. E : B. 3. A : B. 4. B : E. 5. A : D. 6. ? A A 3. 5. B D 4. 1. E 2. B 4. . . etc. The solution is not found, although it exists 36

Propositional logic: summary of typical problems 1. 2. 3. 4. • A proof of a tautology / contradiction Prove that a set of formulas is not satisfiable (Direct / indirect) proof of validity of an argument Inferring consequences of assumptions We can solve by: – – A semantic method, i. e. , by a truth-table or indirectly By means of equivalent transformations – using basic rules of inference (modus ponens, transposition, disjunction elimination) By means of normal forms: conjunctive and disjunctive, i. e. , by a semantic tableau Resolution method: clausal form (conjunctive normal form) Introduction to Logic 37