Discrete Structures Propositional Logic 1 Dr Muhammad Humayoun

Discrete Structures Propositional Logic 1 Dr. Muhammad Humayoun Assistant Professor COMSATS Institute of Computer Science, Lahore. mhumayoun@ciitlahore. edu. pk https: //sites. google. com/a/ciitlahore. edu. pk/dstruct/ 1

Instructor MS in Computer Science and Engineering • Chalmers University of Technology, Sweden. Ph. D in Computer Science • University of Grenoble, France. Post-doc Research Fellow • Pohang University of Science and Technology, South Korea. Specialization: • Human Language Processing, Logic, Proof Theory, Data mining 2

Logistics • Two lectures per week – Each lecture requires reading course book (and an optional reading of reference books) • 3 Quizzes • 3 Assignments • Three exams – Sessional Exam 1 – Sessional Exam 2 – Terminal Exam (15% marks) (10% marks) (15% marks) (50% marks) • Covers all course 3

Logistics Cont. • Course material will be posted on the course website: https: //sites. google. com/a/ciitlahore. edu. pk/dstruct/ • Course representative (CR) can also collect course material from me after every lecture • Other students may get it from him • DON’T individually approach me for the material • CR: Get course handbook and this lecture from me after this class 4

Logistics Cont. • What is on the website: – Course Handbook – Lectures – Assignments – Past quizzes and their solutions – Exams pattern – News • Visit the website frequently 5

Plagiarism • Copying someone else’s work (partial or complete) and submitting it as if it were one’s own • Zero tolerance for plagiarism • Read course handbook to know more about plagiarism 6

Attendance Policy • 80% attendance is mandatory • The students falling short will not be allowed to appear in the Terminal Exam • To get good grade you must attend all the lectures and read suggested material 7

Course Objectives • Deep understanding of discrete structures used in Computer Science • Developing problem solving and analytical skills • Developing algorithmic and computational skills – Ability to understand mathematical arguments and their design – Understanding of logic – Proofing techniques 8

Course Objectives Think Mathematically The very foundation of Computer Science 9

Discrete Structures/Mathematics • Discrete mathematics deals with objects that come in discrete bundles, e. g. , 1 or 2 babies. • Continuous mathematics deals with objects that vary continuously, e. g. , 3. 42 inches from a wall. • Think of digital watches versus analog watches (ones where the second hand loops around continuously without stopping). 10

Discrete vs. Continuous Discrete Continuous 11

Why Study Discrete Structures It is the mathematics underlying almost all of computer science: • Program verification – Analyzing algorithms for correctness and efficiency • Finding efficient algorithms – (for sorting, searching, etc. ) • Formalizing security requirements • Designing cryptographic protocols for enhanced security • Graph Theory (Networks – both physical & social) 12

Course Topics • • • Foundations: Logic Methods of Proof Set Theory Induction and Recursion Counting Relations Graphs Trees Introduction of Algorithms 13

Course requires original thinking • Many students find this course to be significantly more challenging than other courses • Because (among other things), it teaches mathematical reasoning and problem solving – Requires original and deep thinking • Book exercises – A way to let you successfully apply concepts using your own creativity One of the primary goals of this course: • To learn how to attack problems that may be somewhat different from any you may have previously seen 14

Lecture Schedule Weeks Topic of Lecture Reading Assignment Chapter 1 (section 1. 1 and 1. 2), Rosen. Chapter 1 (section 3, 4 and 5), Rosen. Week 1 Foundations: Logic Week 2 Predicate Algebra Week 3 Methods of Proof: Chapter 1 (section 6 and 7), Rosen. Week 4 Set Theory Chapter 2, Rosen. Week 5 SESSIONAL I Exam Paper will be conducted in the first lecture of the week Marked papers will be shown to students and the solution of paper will be discussed in the second lecture of the week 15

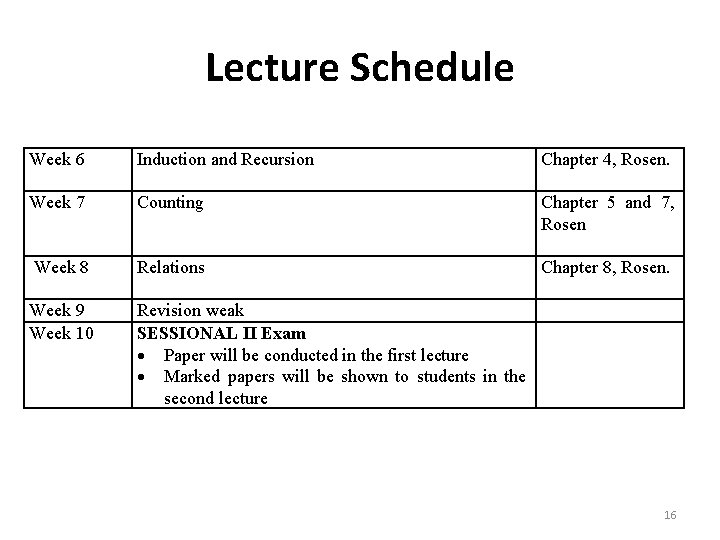
Lecture Schedule Week 6 Induction and Recursion Week 7 Counting Week 8 Relations Week 9 Week 10 Revision weak SESSIONAL II Exam Paper will be conducted in the first lecture Marked papers will be shown to students in the second lecture Chapter 4, Rosen. Chapter 5 and 7, Rosen Chapter 8, Rosen. 16

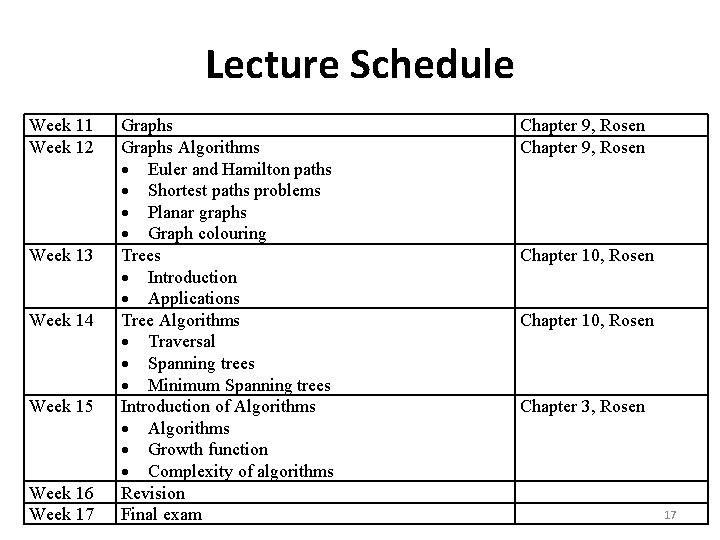
Lecture Schedule Week 11 Week 12 Week 13 Week 14 Week 15 Week 16 Week 17 Graphs Algorithms Euler and Hamilton paths Shortest paths problems Planar graphs Graph colouring Trees Introduction Applications Tree Algorithms Traversal Spanning trees Minimum Spanning trees Introduction of Algorithms Growth function Complexity of algorithms Revision Final exam Chapter 9, Rosen Chapter 10, Rosen Chapter 3, Rosen 17

Recommended Books Course Book • Discrete Mathematics and Its Applications, 6 th Ed. by Kenneth H. Rosen Reference Books: • Discrete Mathematics, 6 th Ed. Richard Johnsonbaugh • Applied Discrete Structures for Computer Science. Pearson Education, Inc. Alan Doerr and Kenneth Levasseur. • Discrete Mathematics Using a Computer. John O’Donnell, Cordelia Hall and Rex Page. 2 nd Ed. Springer. 18

LECTURE 1 Foundations: Logic Chapter 1 Sections 1. 1 and 1. 2 19

Introduction Logic is the study of the principles and methods that distinguishes between a valid an invalid argument Logic deals with general reasoning laws, which you can trust 20

Applications • Applied in proving program correctness and verification • Databases (Relational Algebra and calculus) • Artificial Intelligence 21

Propositional Logic 22

Proposition • 23

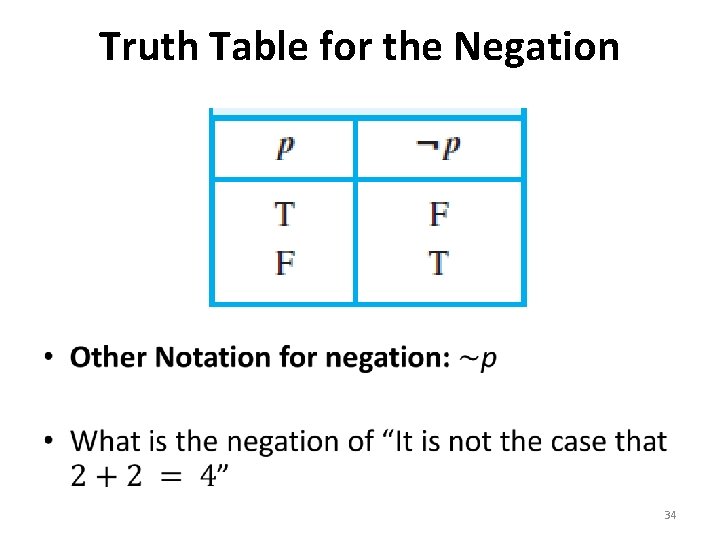
Truth Values • If a proposition is true, we say that it has a truth value of “true” • If a proposition is false, its truth value is “false” • The truth values “true” and “false” are, respectively, denoted by the letters T and F 24

Examples • • 25

Context • 26

Quiz • 27

Quiz • 28

• The area of logic that deals with propositions is called the propositional calculus or propositional logic • It was first developed systematically by the Greek philosopher Aristotle more than 2300 years ago 29

Compound Propositions • Compound propositions, are formed from existing propositions using logical operators (also called as connectives) • The methods to produce new propositions (from those that we already have) were discussed by the English mathematician George Boole in 1854 in his book The Laws of Thought 30

Symbols for Connectives Symbol Meaning Negation Or, disjunction And, conjunction Implication Bi-implication 31

Negation • 32

Examples • 33

Truth Table for the Negation • 34

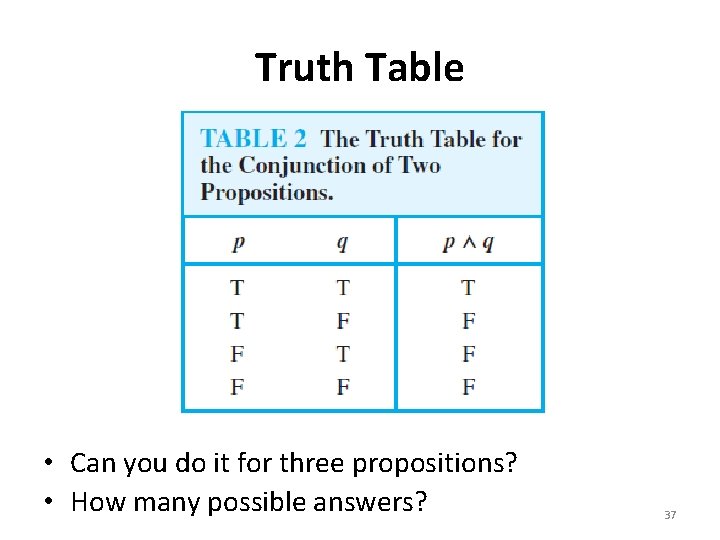
The Conjunction Definition 2 Let p and q be propositions. The conjunction of p and q, denoted by p ∧ q, is the proposition “p and q. ” The conjunction p ∧ q is true when both p and q are true and is false otherwise. 35

Examples • 36

Truth Table • Can you do it for three propositions? • How many possible answers? 37

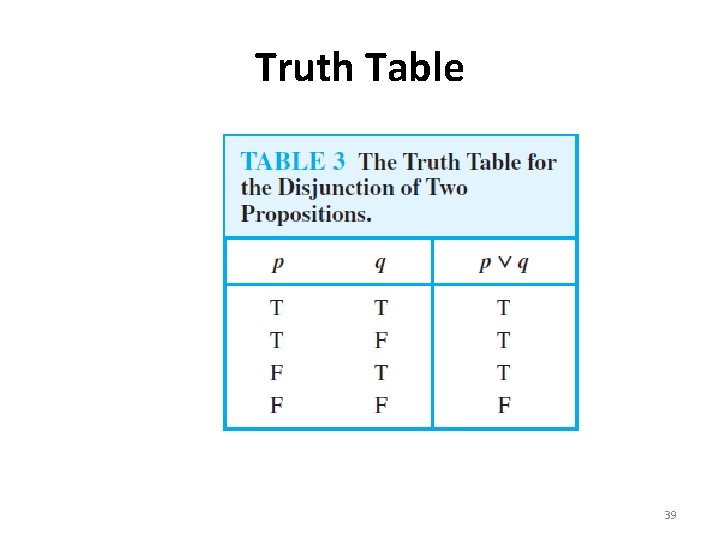
The Disjunction Definition 3 Let p and q be propositions. The disjunction of p and q, denoted by p ∨ q, is the proposition “p or q. ” The disjunction p ∨ q is false when both p and q are false and is true otherwise. 38

Truth Table 39

Inclusive vs. Exclusive “Students who have taken calculus or computer science can take this class. ” (Inclusive or) “Students who have taken calculus or computer science, but not both, can enroll in this class. ” Students who have taken either calculus or computer science, can enroll in this class. (exclusive or) 40

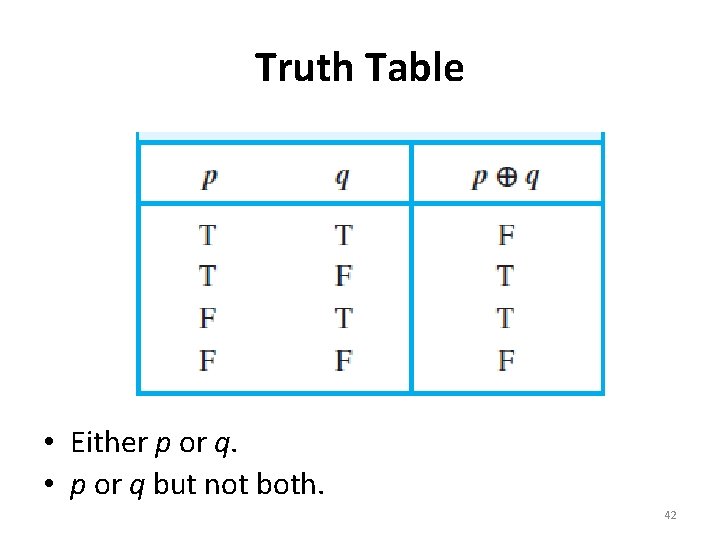
Exclusive Disjunction Definition 4: Let p and q be propositions. The exclusive or of p and q, denoted by p ⊕ q, is the proposition that is true when exactly one of p and q is true and is false otherwise. • Either p or q. • p or q but not both. 41

Truth Table • Either p or q. • p or q but not both. 42

“Inclusive or” or “Exclusive or” “Tonight I will stay home or go out to a movie. ” ? ? ? Human languages can be ambiguous So be careful 43

Conditional Statements/ Implication p: Premise, Hypothesis, antecedent q: Conclusion, Consequence • The statement p → q is true when – both p and q are true – p is false (no matter what truth value q has) 44

Conditional Statements Definition 5: Let p and q be propositions. The conditional statement p → q is the proposition “if p, then q. ” The conditional statement p → q is false when p is true and q is false, and true otherwise. In the conditional statement p → q, p is called the hypothesis (or antecedent or premise) and q is called the conclusion (or consequence). 45

Other forms • Conditional statements play an essential role in mathematical reasoning • Many ways to express an implication (p -> q) : 47

p: you get 100% on the final q: you will get an A p implies that q. you get 100% on the final implies that you will get an A. If p, then q. If you get 100% on the final, then that you will get an A. 48

If p, q. If you get 100% on the final, that you will get an A. p is sufficient for q. Get 100% on the final is sufficient for getting an A. q only if p. you will get an A only if you get 100% on the final. q unless ￢ p. you will get an A unless you don’t get 100% on final. 49

Examples • If I fall in a lake, then I’ll get wet. • If gravity does not exist then I can fly. • If sun rises from the west then it’ll be the end of our planet. • If the moon is made of cheese, then the earth is rectangular. 50

Example Cont. If you get 100% on the final, then you will get an A. • 51

Exercise • Translate the propositions into respective formulae – It is raining and windy. – It is sunny but freezing. – Give me tea or coffee. – If there are DDP students and enrolled in BS, then I will teach DS. 52

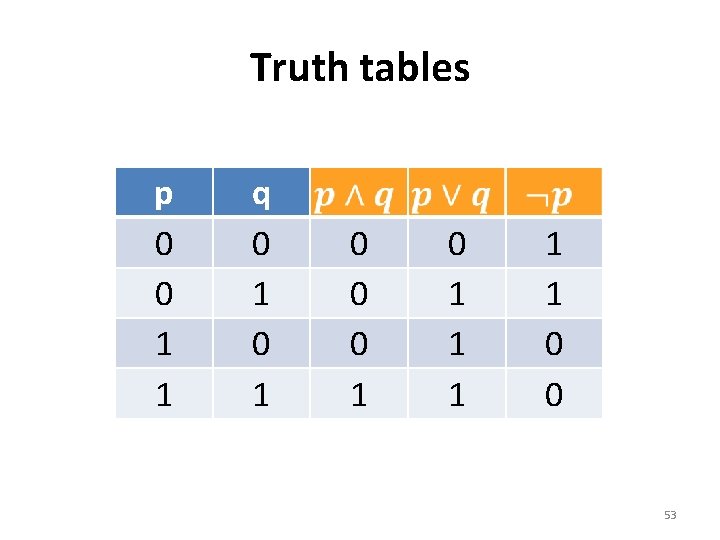
Truth tables p 0 0 1 1 q 0 1 0 0 0 1 1 1 0 0 53

Exercise • Can you complete the following truth table without asking me any question in class? p q r p, q and r are parameters in this exercise 54

Do exercises from the course book 55