PROPOSITIONAL LOGIC Proposition A proposition is a statement

PROPOSITIONAL LOGIC

Proposition A proposition is a statement that is either true or false, but not both. Atlanta was the site of the 1996 Summer Olympic games. 1+1 = 2 3+1 = 5 What will my CS 1050 grade be?

Definition 1. Negation of p Let p be a proposition. The statement “It is not the case that p” is also a proposition, called the “negation of p” or ¬p (read “not p”) p = The sky is blue. p = It is not the case that the sky is blue. p = The sky is not blue. Table 1. The Truth Table for the Negation of a Proposition p ¬p T F F T

Definition 2. Conjunction of p and q Let p and q be propositions. The proposition “p and q, ” denoted by p q is true when both p and q are true and is false otherwise. This is called the conjunction of p and q. Table 2. The Truth Table for the Conjunction of two propositions p q T T F F T F T F F F

Definition 3. Disjunction of p and q Table 3. The Truth Table for the Disjunction of two propositions p q T T F F T F T T T F Let p and q be propositions. The proposition “p or q, ” denoted by p q, is the proposition that is false when p and q are both false and true otherwise.

Definition 4. Exclusive or of p and q Table 4. The Truth Table for the Exclusive OR of two propositions p q T T F F T T F Let p and q be propositions. The exclusive or of p and q, denoted by p q, is the proposition that is true when exactly one of p and q is true and is false otherwise.

Definition 5. Implication p q Let p and q be propositions. The implication p q is the proposition that is false when p is true and q is false, and true otherwise. In this implication p is called the hypothesis (or antecedent or premise) and q is called the conclusion (or consequence). Table 5. The Truth Table for the Implication of p q T T F F T F T T

Implications If p, then q p implies q if p, q p only if q p is sufficient for q q if p q whenever p q is necessary for p Not the same as the if-then construct used in programming languages such as If p then S

Implications How can both p and q be false, and p q be true? • Think of p as a “contract” and q as its “obligation” that is only carried out if the contract is valid. • Example: “If you make more than $25, 000, then you must file a tax return. ” This says nothing about someone who makes less than $25, 000. So the implication is true no matter what someone making less than $25, 000 does. • Another example: p: Bill Gates is poor. q: Pigs can fly. p q is always true because Bill Gates is not poor. Another way of saying the implication is “Pigs can fly whenever Bill Gates is poor” which is true since neither p nor q is true.

Related Implications Converse of p q is q p Contrapositive of p q is the proposition q p Inverse of p q Is the proposition p q

Example implication: “If it rains today, I will go to college tomorrow” Converse: I will go to college tomorrow only if it rains today Contrapositive : If I do not go to college tomorrow, then it will not have rained today Inverse : If it does not rain today, then I will not go to college tomorrow

Definition 6. Biconditional Table 6. The Truth Table for the biconditional p q T T F F T F T F F T Let p and q be propositions. The biconditional p q is the proposition that is true when p and q have the same truth values and is false otherwise. “p if and only if q, p is necessary and sufficient for q”

Practice p: You learn the simple things well. q: The difficult things become easy. The difficult things You do not learn the become easy but you simple things well. p did not learn the simple If you learn the simple things well then the q p You learn the simple difficult things become things well but the easy. p q difficult things did not If you do not learn the become easy. simple things well, then the difficult things will not p q become easy. p q

Truth Table Puzzle Steve would like to determine the relative salaries of three coworkers using two facts (all salaries are distinct): If Fred is not the highest paid of the three, then Janice is. If Janice is not the lowest paid, then Maggie is paid the most. Who is paid the most and who is paid the least?

p : Janice is paid the most. q: Maggie is paid the most. r: Fred is paid the most. s: Janice is paid the least. p T F F q F T F r F F T s F T T F F Fred, Maggie, Janice r p T F T • If Fred is not the highest paid of the three, then Janice is. • If Janice is not the lowest paid, then Maggie is paid the most. s q ( r p) ( s q) F F T T T F F F

p : Janice is paid the most. q: Maggie is paid the most. r: Fred is paid the most. s: Janice is paid the least. p T F F q F T F r F F T s F T T F F r p T F T • If Fred is not the highest paid of the three, then Janice is. • If Janice is the lowest paid, then Maggie is paid the most. s q T T F T T ( r p) (s q) T F F F T Fred, Janice, Maggie or Janice, Maggie, Fred or Janice, Fred, Maggie

Well formed Formula (WFF) A well formed formula can be produced using following rules: Rule 1 : A statement variable itself is a WFF Rule 2 : If p is WFF, then p is WFF Rule 3 : If p and q are WFF then (p q), (p q) and (p q) are also WFF Rule 4 : A string of symbols consisting of statement variables, connectives and parentheses is said to be WFF iff it can be produced by applying rule 1, 2 and 3 finitely many times

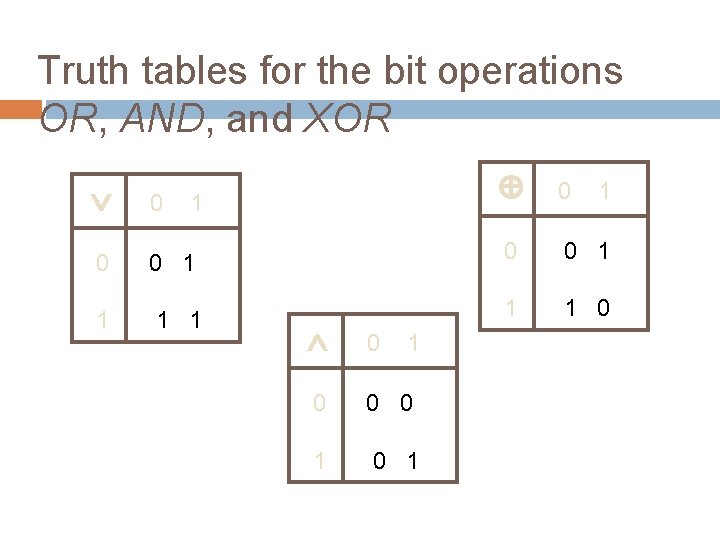
Bit Operations A computer bit has two possible values: 0 (false) and 1 (true). A variable is called a Boolean variable is its value is either true or false. Bit operations correspond to the logical connectives: OR AND XOR Information can be represented by bit strings, which are sequences of zeros and ones, and manipulated by operations on the bit strings.

Truth tables for the bit operations OR, AND, and XOR 0 0 1 1 1 0 0 0 1 1 0 0 1 0 1 1 1

Logical Equivalence An important technique in proofs is to replace a statement with another statement that is “logically equivalent. ” Tautology: compound proposition that is always true regardless of the truth values of the propositions in it. Eg. p p Contradiction: Compound proposition that is always false regardless of the truth values of the propositions in it. Eg. p p

Logically Equivalent Compound propositions P and Q are logically equivalent if P Q is a tautology. In other words, P and Q have the same truth values for all combinations of truth values of simple propositions. This is denoted: P Q (or by P Q)

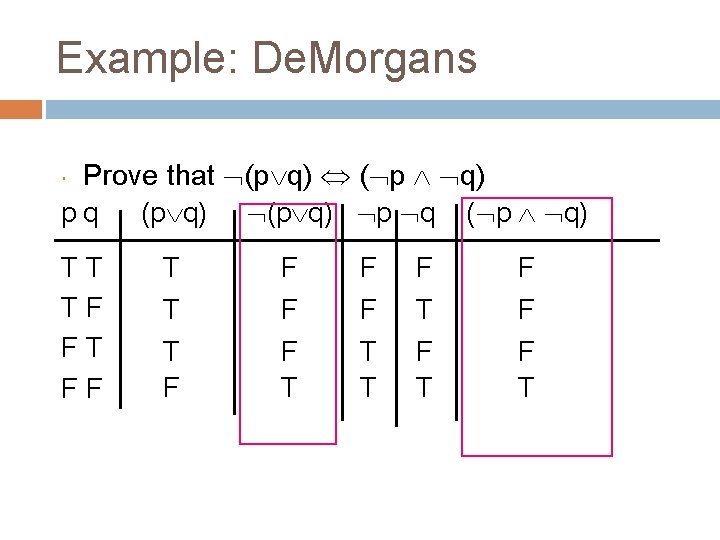
Example: De. Morgans Prove that (p q) ( p q) pq (p q) p q ( p q) TT TF FT FF T F F T T F F F T T T F F T

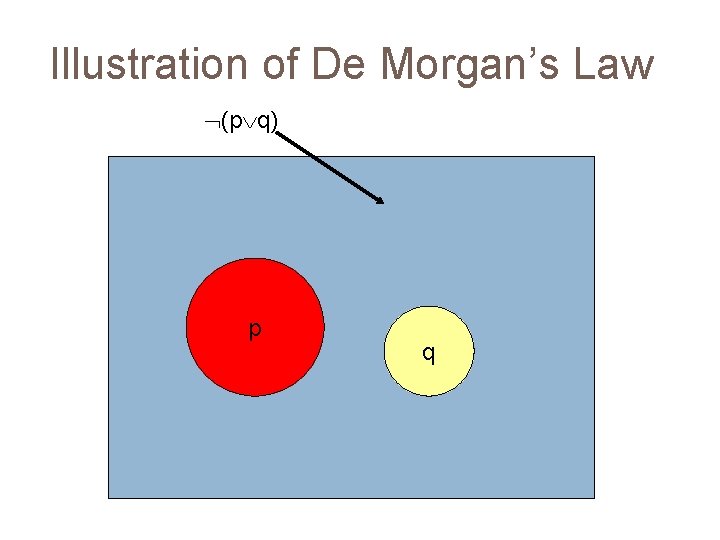
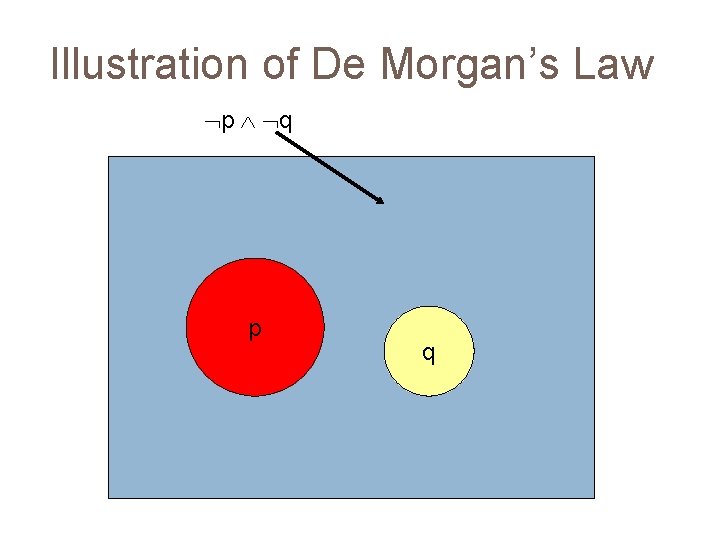
Illustration of De Morgan’s Law (p q) p q

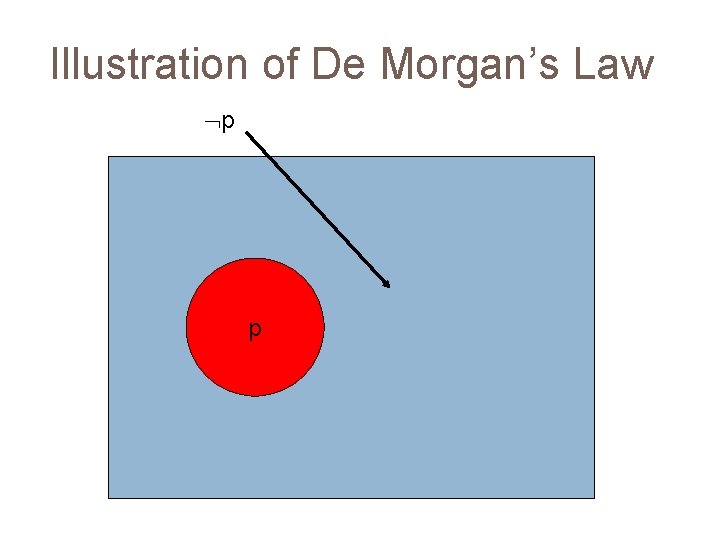
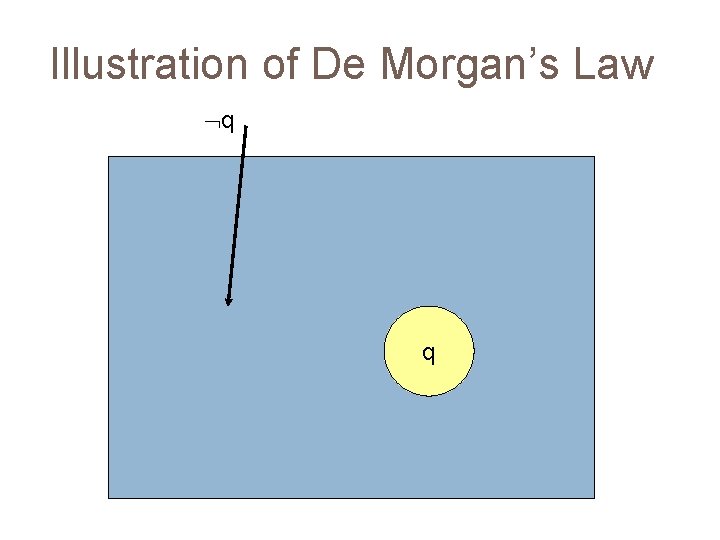
Illustration of De Morgan’s Law p p

Illustration of De Morgan’s Law q q

Illustration of De Morgan’s Law p q p q

Example: Distribution Prove that: p (q r) (p q) (p r) p T T F F q T T F F r T F T F q r p (q r) p q T T T F T T T F F F F p r T T T F (p q) (p r) T T T F F F

Prove: p q (p q) (q p) pq TT TF FT FF p q T F F T p q q p T T F T T (p q) (q p) T F F T We call this biconditional equivalence.

List of Logical Equivalences p T p; p F p Identity Laws p T T; p F F Domination Laws p p p; p p p Idempotent Laws ( p) p Double Negation Law p q q p; p q q p Commutative Laws (p q) r p (q r); (p q) r p (q r) Associative Laws

List of Equivalences p (q r) (p q) (p r) Distribution Laws (p q) ( p q) De Morgan’s Laws p p T p p F (p q) ( p q) Miscellaneous Or Tautology And Contradiction Implication Equivalence p q (p q) (q p) Biconditional Equivalence