Stochastic rounding and reducedprecision fixedpoint arithmetic for solving

Stochastic rounding and reducedprecision fixed-point arithmetic for solving neural ODEs Steve Furber, Mantas Mikaitis, Michael Hopkins, David Lester Advanced Processor Technologies research group The University of Manchester 1

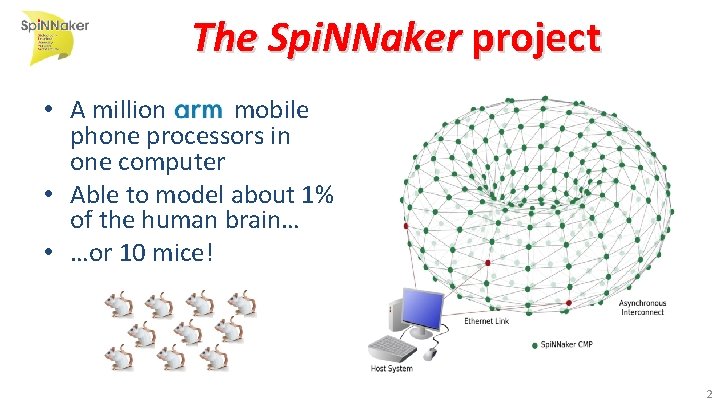
The Spi. NNaker project • A million mobile phone processors in one computer • Able to model about 1% of the human brain… • …or 10 mice! 2

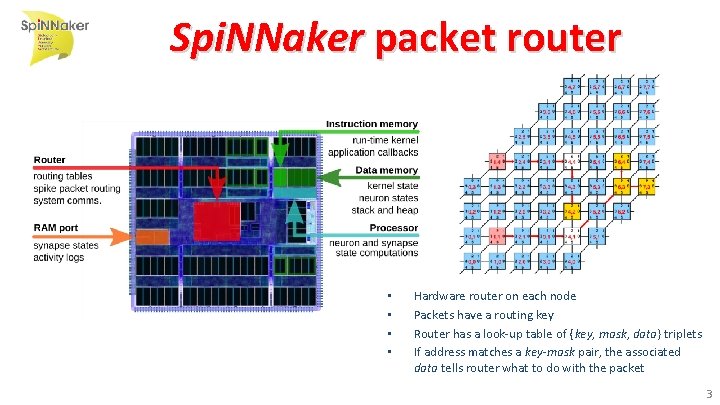
Spi. NNaker packet router • • Hardware router on each node Packets have a routing key Router has a look-up table of {key, mask, data} triplets If address matches a key-mask pair, the associated data tells router what to do with the packet 3

Spi. NNaker machines Spi. NNaker board (864 ARM cores) • HBP platform – 1 M cores – 11 cabinets (including server) • Launch 30 March 2016 – then 500 k cores Spi. NNaker chip (18 ARM cores) 4

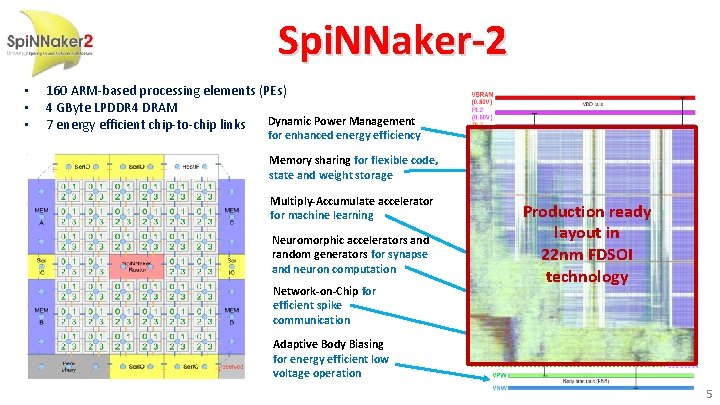
Spi. NNaker-2 • • • 160 ARM-based processing elements (PEs) 4 GByte LPDDR 4 DRAM Dynamic Power Management 7 energy efficient chip-to-chip links for enhanced energy efficiency Memory sharing for flexible code, state and weight storage Multiply-Accumulate accelerator for machine learning Neuromorphic accelerators and random generators for synapse and neuron computation Network-on-Chip for efficient spike communication Production ready layout in 22 nm FDSOI technology Adaptive Body Biasing for energy efficient low voltage operation 5

Motivation for reduced precision • • Energy-efficiency Memory footprint Memory bandwidth Spi. NNaker: – ARM 968 has no floatingpoint hardware – Cortex M 4 F has 32 -bit FP Energy per operation: • 64 -bit float MAF 20 p. J • 32 -bit float MAF 6 p. J • 32 -bit int MADD 4 p. J • 16 -bit int MADD 1 p. J data: Simon Knowles (Graph. Core), 28 nm 0 v 8 6

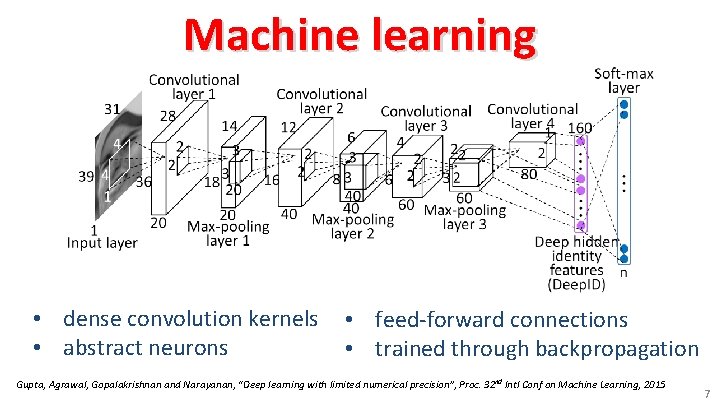
Machine learning • dense convolution kernels • abstract neurons • feed-forward connections • trained through backpropagation Gupta, Agrawal, Gopalakrishnan and Narayanan, “Deep learning with limited numerical precision”, Proc. 32 nd Intl Conf on Machine Learning, 2015 7

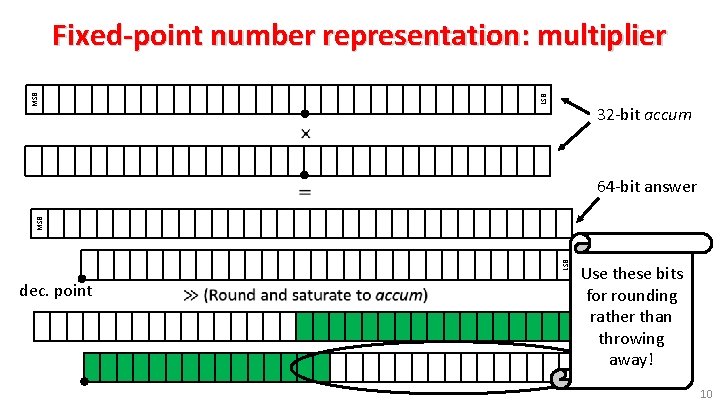
Fixed-point number representation LSB MSB Standard (non-floating-point) CPU arithmetic is integer • add, subtract, multiply (with accumulate? ) • divide (sometimes – not on ARM 968!) Fixed-point arithmetic maps onto these integer operations • interpret integer as scaled by 2 -n • arithmetic operations work as expected (mainly!) • e. g. GCC accum s 16. 15 type: 8

Fixed-point number representation … … . … … • 9

LSB MSB Fixed-point number representation: multiplier 32 -bit accum 64 -bit answer LSB MSB dec. point Use these bits for rounding rather than throwing away! 10

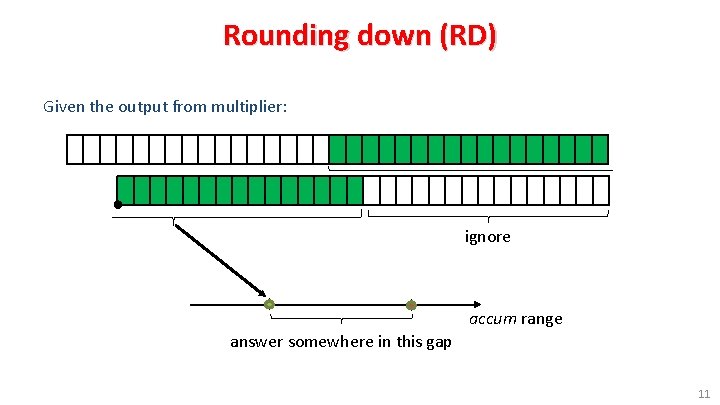
Rounding down (RD) Given the output from multiplier: ignore accum range answer somewhere in this gap 11

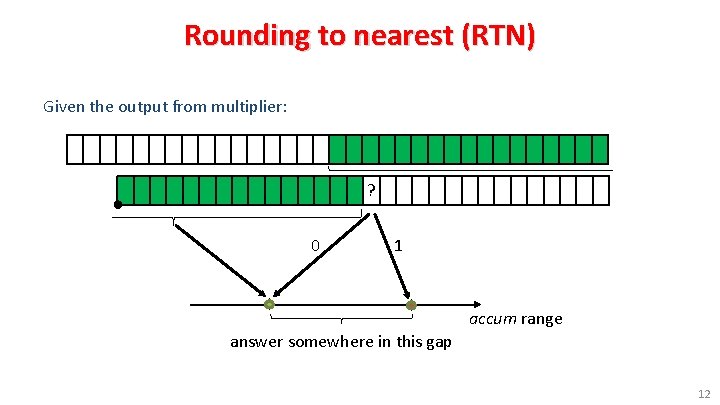
Rounding to nearest (RTN) Given the output from multiplier: ? 0 1 accum range answer somewhere in this gap 12

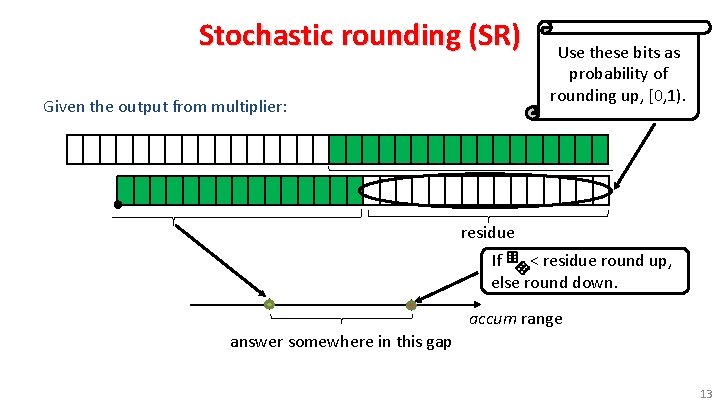
Stochastic rounding (SR) Given the output from multiplier: Use these bits as probability of rounding up, [0, 1). residue If < residue round up, else round down. accum range answer somewhere in this gap 13

Ordinary Differential Equations (ODEs) • What are they? Define time evolution of the state variables of a system via differential equations • Where are they used? Neuroscience, physics, chemistry, biology, ecology, pharmacology, meteorology, astronomy, epidemiology, population modelling, … Izhikevich ODE used widely in computational neuroscience On spiking (V > 30 m. V): 14

Example Neural ODE behaviour RS neuron FS neuron (a = 0. 02, b = 0. 2, c = -65. 0, d = 8. 0) (a = 0. 1, b = 0. 2, c = -65. 0, d = 2. 0) 4. 775 n. A DC current input after 60 ms Mathematica algorithmic reference 15

Arithmetic types used for comparison • 64 -bit IEEE double-precision floating-point (reference) • 32 -bit IEEE single-precision floating-point • 32 -bit accum s 16. 15 fixed-point (with 3 rounding modes) Also discussed in the paper… • 32 -bit s 0. 31 fixed-point (if mixed-precision required) • 16 -bit s 8. 7 fixed-point (with 3 rounding modes) 16

Solver algorithms and ESR We implement 4 explicit ODE solvers… • and combine with Izhikevich equation • using ESR (Explicit Solver Reduction) technique – (for details see: Hopkins & Furber (2015), Neural Computation) 1. 2. 3. 4. Runge-Kutta 2 nd order Midpoint Runge-Kutta 2 nd order Trapezoid Runge-Kutta 3 rd order Heun Chan-Tsai hybrid 17

Arithmetic detail • Rounding constants within ODE definitions – – – e. g. exact = 0. 04 = 1310. 72 / 215 s 16. 15 (RD) = 0. 0399780… = 1310 / 215 s 16. 15 (RTN) = 0. 0400085… = 1311 / 215 s 0. 31 (RTN) = 0. 040000372529 float = 0. 03999999910593… • GCC surprise – RTN not implemented for fixed-point – using RTN instead of RD above improves accuracy a lot! • Mixed precision multiplies - accum x fract • Automated test bench using C macros to switch options 18

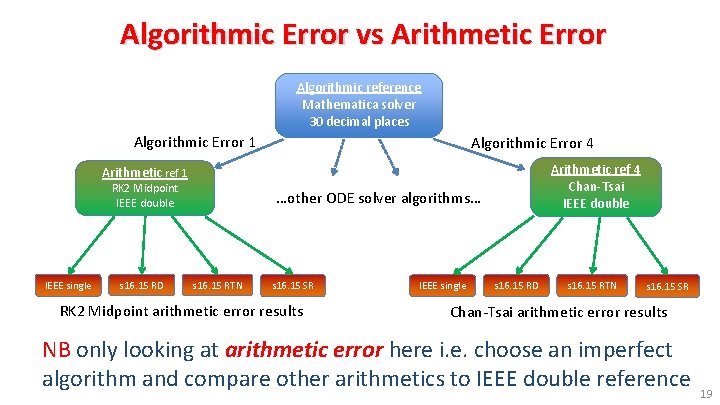
Algorithmic Error vs Arithmetic Error Algorithmic reference Mathematica solver 30 decimal places Algorithmic Error 1 Algorithmic Error 4 Arithmetic ref 4 Chan-Tsai IEEE double Arithmetic ref 1 RK 2 Midpoint IEEE double IEEE single s 16. 15 RD …other ODE solver algorithms… s 16. 15 RTN s 16. 15 SR RK 2 Midpoint arithmetic error results IEEE single s 16. 15 RD s 16. 15 RTN s 16. 15 SR Chan-Tsai arithmetic error results NB only looking at arithmetic error here i. e. choose an imperfect algorithm and compare other arithmetics to IEEE double reference 19

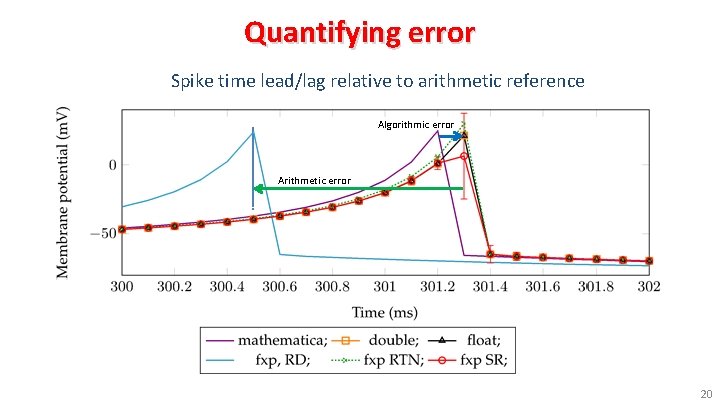
Quantifying error Spike time lead/lag relative to arithmetic reference Algorithmic error Arithmetic error 20

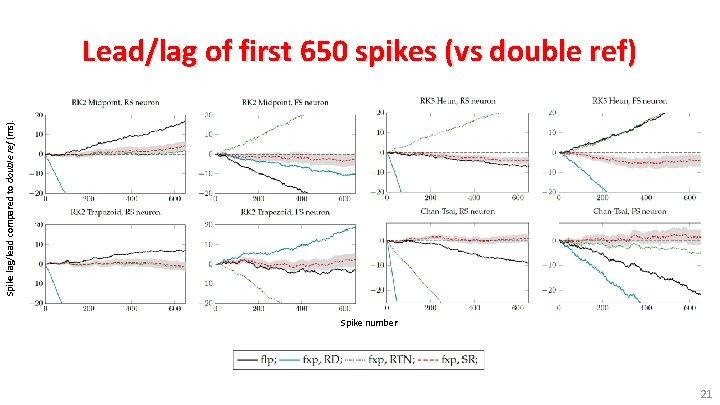
Spike lag/lead compared to double ref (ms). Lead/lag of first 650 spikes (vs double ref) Spike number 21

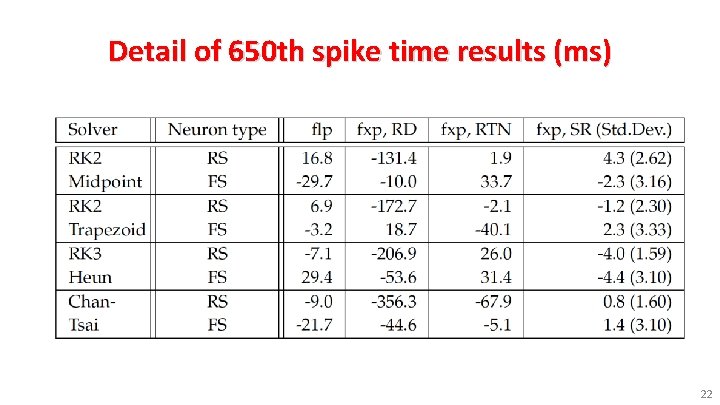
Detail of 650 th spike time results (ms) 22

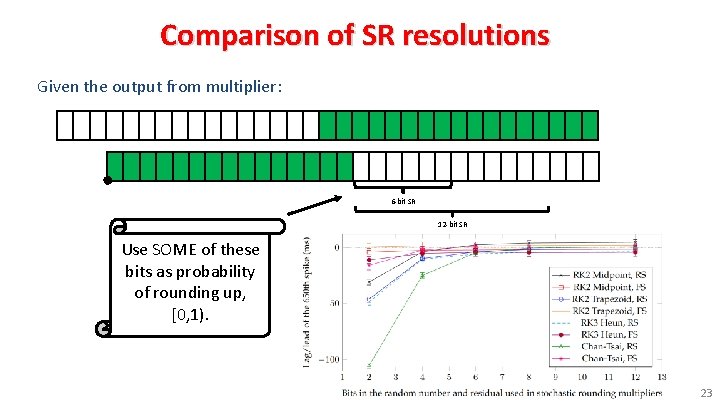
Comparison of SR resolutions Given the output from multiplier: 6 -bit SR 12 -bit SR Use SOME of these bits as probability of rounding up, [0, 1). 23

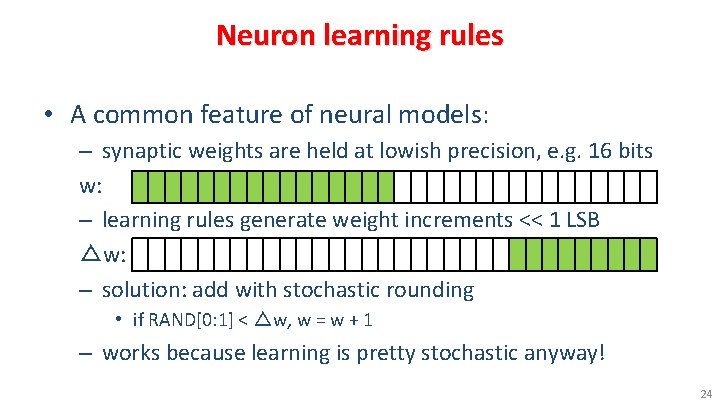
Neuron learning rules • A common feature of neural models: – synaptic weights are held at lowish precision, e. g. 16 bits w: – learning rules generate weight increments << 1 LSB △w: – solution: add with stochastic rounding • if RAND[0: 1] < △w, w = w + 1 – works because learning is pretty stochastic anyway! 24

Dither • Vanderkooy and Lipshitz, “Dither in digital audio”, J. Audio Eng. Soc. 1987 25

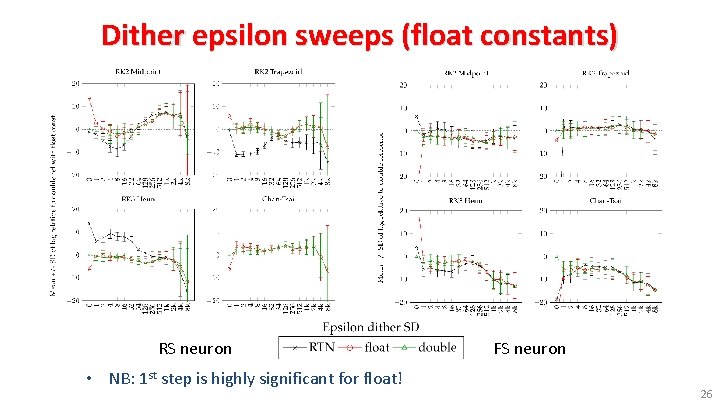
Dither epsilon sweeps (float constants) RS neuron FS neuron • NB: 1 st step is highly significant for float! 26

Conclusions • There is growing interest in reduced precision number representations in many areas of computing – To reduce memory footprint, energy requirements, etc. • Lower precision incurs accuracy issues • Stochastic rounding gives optimal accuracy • Stochastic rounding can also address scaling mismatch in weight increment • Dither techniques are simpler and may perform adequately? 27