Discrete Mathematics Lecture 3 Applications of Propositional Logic

Discrete Mathematics Lecture 3: Applications of Propositional Logic and Propositional Equivalences By: Nur Uddin, Ph. D 1

Applications of Propositional Logic 1. Translating sentences 2. System specification 3. Boolean search 4. Logic puzzles 5. Logic circuits 2

Applications of Propositional Logic 1. Translating sentences Example: You can access the Internet from campus only if you are a computer science major or you are not a freshman. 3

Applications of Propositional Logic 2. System specification Example 1: The automated reply cannot be sent when the file system is full Example 2: 4

Applications of Propositional Logic 2. System specification Example 2: 5

Applications of Propositional Logic 3. Boolean search Google search is the example 6

Applications of Propositional Logic 4. Logic Puzzles Example: In [Sm 78] Smullyan posed many puzzles about an island that has two kinds of inhabitants, knights, who always tell the truth, and their opposites, knaves, who always lie. You encounter two people A and B. What are A and B if A says “B is a knight” and B says “The two of us are opposite types? ” 7

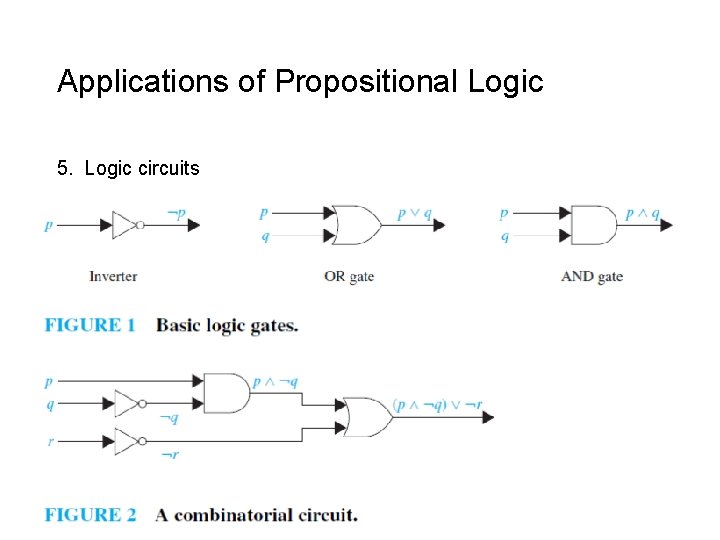
Applications of Propositional Logic 5. Logic circuits 8

Propositional Equivalences Definition • A compound proposition that is always true, no matter what the truth values of the propositional variables that occur in it, is called a tautology. • A compound proposition that is always false is called a contradiction. • A compound proposition that is neither a tautology nor a contradiction is called a contingency. 9

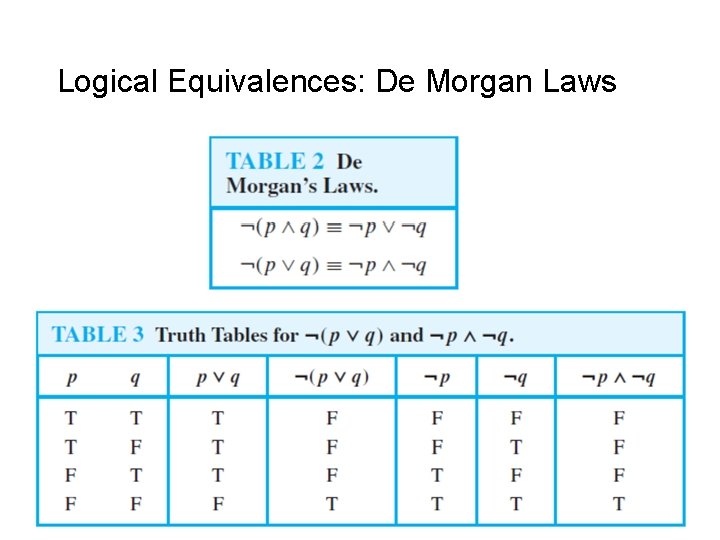
Logical Equivalences • Compound propositions that have the same truth values in all possible cases are called logically equivalent. • The compound propositions p and q are called logically equivalent if p ↔ q is a tautology. • The notation p ≡ q denotes that p and q are logically equivalent. 10

Logical Equivalences: De Morgan Laws 11

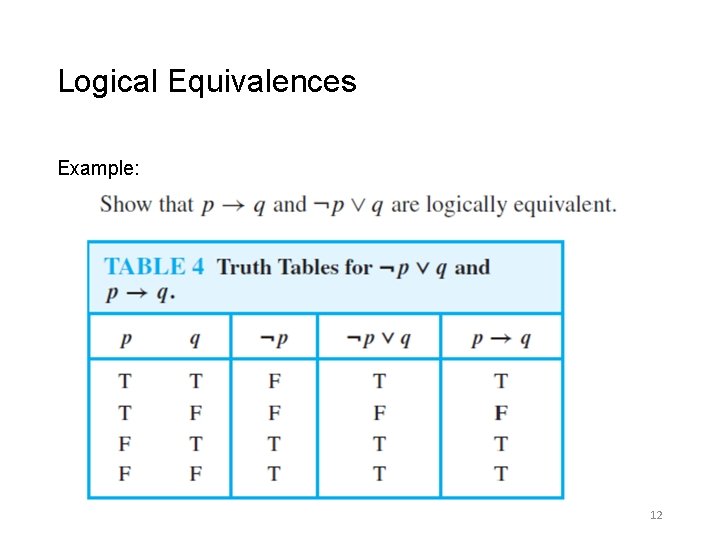
Logical Equivalences Example: 12

Logical Equivalences 13

Logical Equivalences 14

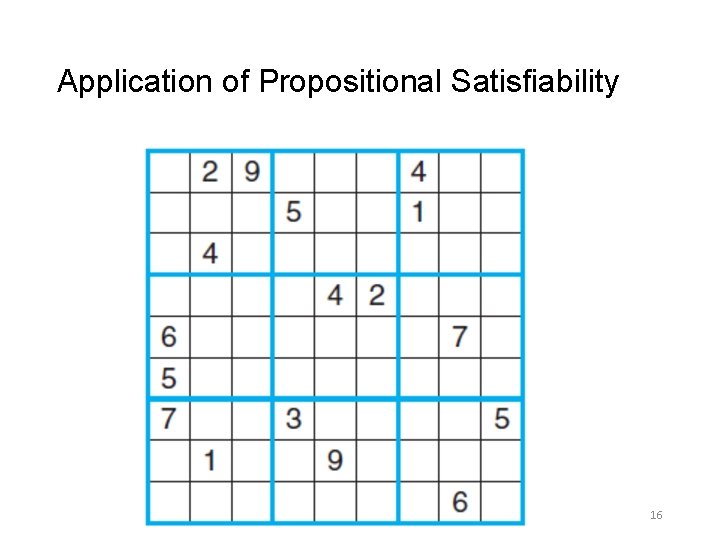
Propositional Satisfiability • A compound proposition is satisfiable if there is an assignment of truth values to its variables that makes it true. • Example: Check satisfiability of the following compound propositions a. (p ∨￢q) ∧ (q ∨￢r) ∧ (r ∨￢p) b. (p ∨ q ∨ r) ∧ (￢p ∨￢q ∨￢r) c. (p ∨ q ∨ r) ∧ (￢p ∨￢q ∨￢r) • When we find a particular assignment of truth values that makes a compound proposition true, we have shown that it is satisfiable; such an assignment is called a solution of this particular satisfiability problem. 15

Application of Propositional Satisfiability 16