Discrete Mathematics Propositional Equivalence 2014 Tautology Contradiction Propositional

이산수학(Discrete Mathematics) 명제의 동치 (Propositional Equivalence) 2014년 봄학기 강원대학교 컴퓨터과학전공 문양세

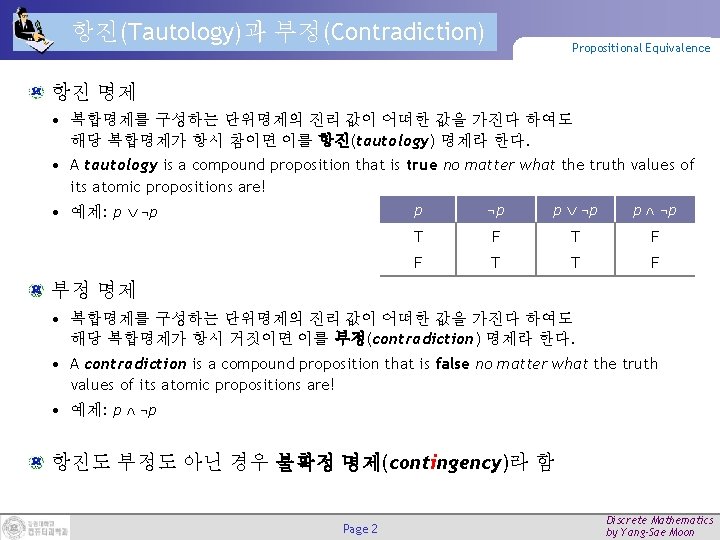
항진(Tautology)과 부정(Contradiction) Propositional Equivalence 항진 명제 • 복합명제를 구성하는 단위명제의 진리 값이 어떠한 값을 가진다 하여도 해당 복합명제가 항시 참이면 이를 항진(tautology) 명제라 한다. • A tautology is a compound proposition that is true no matter what the truth values of its atomic propositions are! p ¬p p ¬p • 예제: p ¬p T F F T T F 부정 명제 • 복합명제를 구성하는 단위명제의 진리 값이 어떠한 값을 가진다 하여도 해당 복합명제가 항시 거짓이면 이를 부정(contradiction) 명제라 한다. • A contradiction is a compound proposition that is false no matter what the truth values of its atomic propositions are! • 예제: p ¬p 항진도 부정도 아닌 경우 불확정 명제(contingency)라 함 Page 2 Discrete Mathematics by Yang-Sae Moon

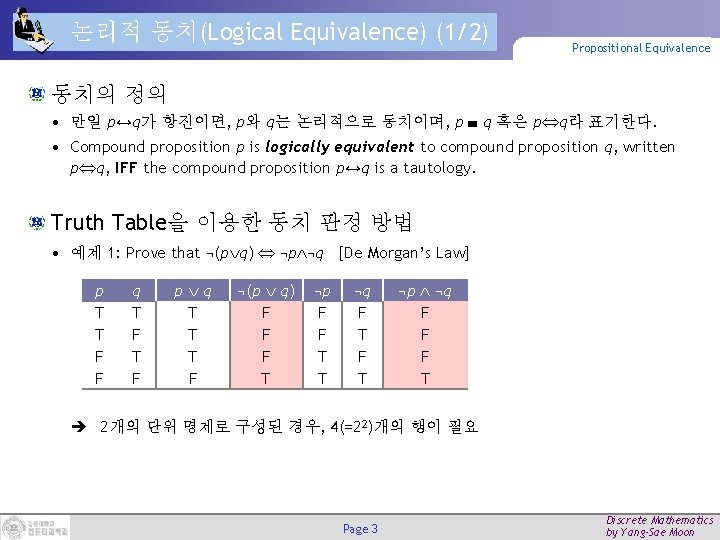
논리적 동치(Logical Equivalence) (1/2) Propositional Equivalence 동치의 정의 • 만일 p↔q가 항진이면, p와 q는 논리적으로 동치이며, p q 혹은 p q라 표기한다. • Compound proposition p is logically equivalent to compound proposition q, written p q, IFF the compound proposition p↔q is a tautology. Truth Table을 이용한 동치 판정 방법 • 예제 1: Prove that ¬(p q) ¬p ¬q [De Morgan’s Law] p T T F F q T F p q T T T F ¬(p q) F F F T ¬p F F T T ¬q F T ¬p ¬q F F F T 2개의 단위 명제로 구성된 경우, 4(=22)개의 행이 필요 Page 3 Discrete Mathematics by Yang-Sae Moon

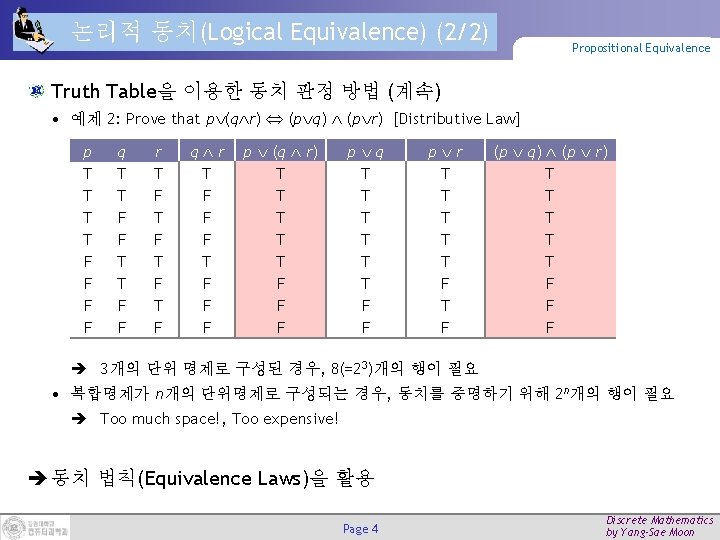
논리적 동치(Logical Equivalence) (2/2) Propositional Equivalence Truth Table을 이용한 동치 판정 방법 (계속) • 예제 2: Prove that p (q r) (p q) (p r) [Distributive Law] p T T F F q T T F F r T F T F q r T F F F p (q r) T T T F F F p q T T T F F p r T T T F (p q) (p r) T T T F F F 3개의 단위 명제로 구성된 경우, 8(=23)개의 행이 필요 • 복합명제가 n개의 단위명제로 구성되는 경우, 동치를 증명하기 위해 2 n개의 행이 필요 Too much space!, Too expensive! 동치 법칙(Equivalence Laws)을 활용 Page 4 Discrete Mathematics by Yang-Sae Moon

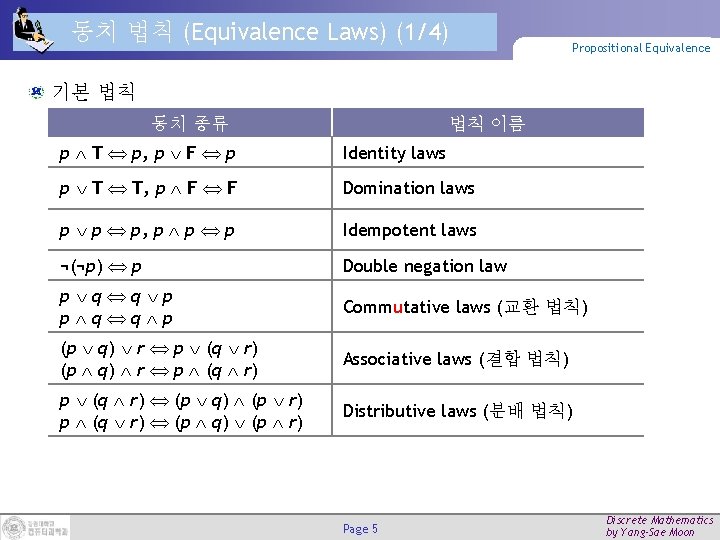
동치 법칙 (Equivalence Laws) (1/4) Propositional Equivalence 기본 법칙 동치 종류 법칙 이름 p T p, p F p Identity laws p T T, p F F Domination laws p p p, p p p Idempotent laws ¬(¬p) p Double negation law p q q p Commutative laws (교환 법칙) (p q) r p (q r) Associative laws (결합 법칙) p (q r) (p q) (p r) Distributive laws (분배 법칙) Page 5 Discrete Mathematics by Yang-Sae Moon

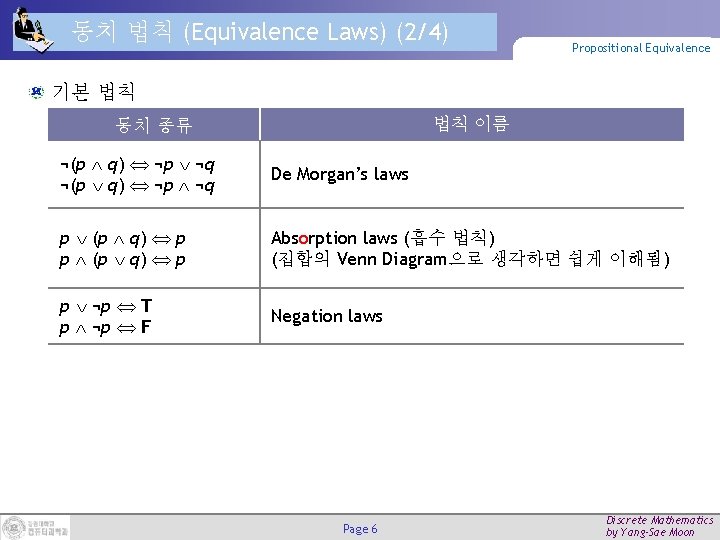
동치 법칙 (Equivalence Laws) (2/4) Propositional Equivalence 기본 법칙 법칙 이름 동치 종류 ¬(p q) ¬p ¬q De Morgan’s laws p (p q) p Absorption laws (흡수 법칙) (집합의 Venn Diagram으로 생각하면 쉽게 이해됨) p ¬p T p ¬p F Negation laws Page 6 Discrete Mathematics by Yang-Sae Moon

동치 법칙 (Equivalence Laws) (3/4) Propositional Equivalence 함축을 포함한 논리적 동치 • p q ¬p q • p q ¬p q • p q ¬(p ¬q) [try it!] • (p q) (p r) p (q r) • (p r) (q r) (p q) r Page 7 Discrete Mathematics by Yang-Sae Moon

동치 법칙 (Equivalence Laws) (4/4) Propositional Equivalence 상호조건을 포함한 논리적 동치 • p ↔ q (p q) (q p) • p ↔ q ¬p ↔ ¬q [try it!] (대우 활용) • p ↔ q (p q) (¬p ¬q) Page 8 Discrete Mathematics by Yang-Sae Moon

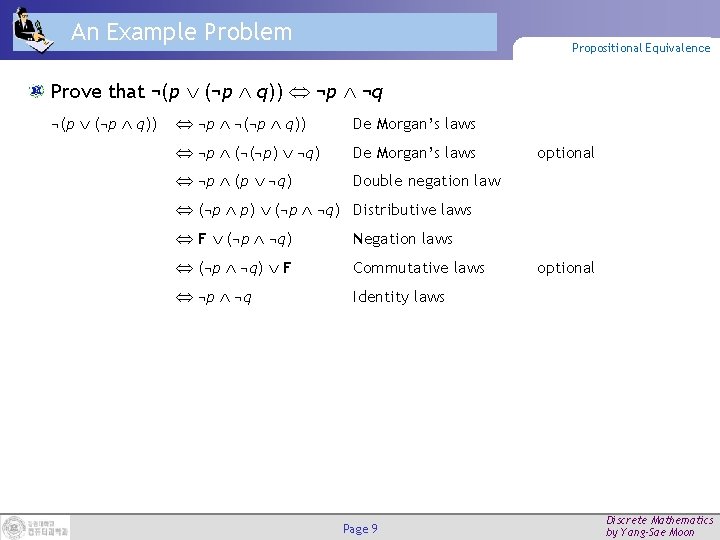
An Example Problem Propositional Equivalence Prove that ¬(p (¬p q)) ¬p ¬q ¬(p (¬p q)) ¬p ¬(¬p q)) De Morgan’s laws ¬p (¬(¬p) ¬q) De Morgan’s laws ¬p (p ¬q) Double negation law optional (¬p p) (¬p ¬q) Distributive laws F (¬p ¬q) Negation laws (¬p ¬q) F Commutative laws ¬p ¬q Identity laws Page 9 optional Discrete Mathematics by Yang-Sae Moon