Lecture 1 0 INTRODUCTION TO DISCRETE MATHEMATICS Discrete

Lecture 1 0. INTRODUCTION TO DISCRETE MATHEMATICS Discrete Mathematics Dr. -Ing. Erwin Sitompul http: //zitompul. wordpress. com

Text Book and Syllabus Text book: Kenneth H. Rosen, “Discrete Mathematics and Its Applications”, 6 th Edition, Mc. Graw-Hill International Edition, 2007. Syllabus: 1. 2. 3. 4. 5. 6. Logic and Proofs Sets Relation and Functions Mathematical Induction Counting and Combinatorial Graphs Erwin Sitompul Discrete Mathematics 1/2

Grade Policy Final Grade = 10% Homework + 20% Quizzes + 30% Midterm Exam + 40% Final Exam + Extra Points § Homeworks will be given in fairly regular basis. The average of homework grades contributes 10% of final grade. § Homeworks must be written on A 4 papers. § Homeworks must be submitted on time. If you submit late, < 10 min. No penalty 10 – 60 min. – 20 points > 60 min. – 40 points § There will be 3 quizzes along the semester. The average of the best 2 will be counted. The quizes contribute 30% of final grade. § Midterm and final exam schedule will be announced in time. § Make up of quizzes and exams will be held one week after the schedule of the respective quizzes and exams. Erwin Sitompul Discrete Mathematics 1/3

Lecture Material § New lecture slides will be available on internet every week. Please check the course homepage regularly. § The course homepage is : http: //zitompul. wordpress. com § You are responsible to read and understand the lecture slides. If there is any problem, you may ask me. § Quizzes, midterm exam, and final exam will be closed-book. But you may bring an A 5 cheat sheet for quizzes and A 4 cheat sheet for mid and final exam. § Extra points will be given if you solve a problem in front of the class. You will earn 1, 2, or 3 points. Erwin Sitompul Discrete Mathematics 1/4

What is “Discrete Mathematics”? Discrete Mathematics is a branch of mathematics that discuss about discrete objects or components. What is the definition of discrete? An object can be said to be discrete if : § It consists of unconnected distinct parts/ members § It consists of finite or countable parts/ members. Example: § A set of female IR 2009 students § A set of positive integers Erwin Sitompul Discrete Mathematics 1/5

What is “Discrete Mathematics”? The opposite of discrete is continuous. All engineers take mathematics through Calculus and differential equations, but IE is different in that it is based on “discrete variable” math, whereas all other engineering is based on “continuous variable” math. The emphasis on discrete mathematics, along with linear algebra and difference equation, distinguishes Industrial Engineering from other engineering disciplines. Erwin Sitompul Discrete Mathematics 1/6

What is “Discrete Mathematics”? Discrete Mathematics can find unique applications in IE on Production Systems such as: • • • Sequencing orders Scheduling batches Determining the number of materials handling units Arranging factory layouts Finding sequences of motions etc. Erwin Sitompul Discrete Mathematics 1/7

What is “Discrete Mathematics”? Some examples of problems related with discrete mathematics problems: § How many different password can be made out of 8 different characters? § How does a ISBN number of a book or a credit card number is validated? § How many 8 -bit-long binary string combinations can be made if the sum of bit-1 must be odd? § How to determine the shortest path between point A and point B in a factory complex? § Proof that a combination of 3 s and 5 s can result any integer number higher than 8. Erwin Sitompul Discrete Mathematics 1/8

What is “Discrete Mathematics”? Some examples of problems related with discrete mathematics problems: § How to construct logic circuit for a seven segments? § Can you walk through all the streets in your housing complex exactly once and come back to the original position? § “Cheap food is not tasty. ” “Tasty food is not cheap. ” Are both statements telling us the same thing? Erwin Sitompul Discrete Mathematics 1/9

Lecture 1 1. LOGIC AND PROOFS Discrete Mathematics Dr. -Ing. Erwin Sitompul http: //zitompul. wordpress. com

Logic and Proposition Logic: § Logic is the basic of reasoning. § Reasoning is based on relations between propositions. Proposition: § A proposition is a statement that can be either true (T) or false (F), but not both. § The synonym of proposition is open sentence. Erwin Sitompul Discrete Mathematics 1/11

Proposition Example: (Propositions) § § § § 13 is an odd number. Ir. Soekarno was graduated from UGM. 1 + 1 = 2. 8 square root of (8 + 8). There is monkey in the moon. Today is Wednesday. For any integer n 0, there exists 2 n which is an even number. § x + y = y + x for any real number x and y. Erwin Sitompul Discrete Mathematics 1/12

Proposition Example: (Not Propositions) § § § What time does Argo Bromo train arrive at Gambir Station? Do the quiz without cooperating! x = 3 + 8. x > 5. I am heavy. Conclusion: Propositions are declarative sentences. Conclusion: If a proposition is made out of mathematical equations, then the equations must posses an answer so that its truth value can be evaluated. Erwin Sitompul Discrete Mathematics 1/13

Propositions are denoted with lower case letters starting with p such as p, q, r, … Example: § p : 13 is an odd number. § q : Ir. Soekarno was graduated from UGM. § r : 2 + 2 = 4. Erwin Sitompul Discrete Mathematics 1/14

Combining Propositions Given propositions p and q, then: 1. Negation of p : not p, 2. Conjunction : p and q, 3. Disjunction : p or q, p, ¬p p q Consisting only a single statement, each p and q is called atomic proposition. Combination of p and q results in a compound proposition. Erwin Sitompul Discrete Mathematics 1/15

Combining Propositions Example: The following prepositions are known p : Today is rainy. q : The class is cancelled. p q : Today is rainy and the class is cancelled. p q : Today is rainy or the class is cancelled. p : It is not true that today is rainy. (or: Today is not rainy) Erwin Sitompul Discrete Mathematics 1/16

Combining Propositions Example: Given the following propositions, p : The girl is beautiful. q : The girl is smart. Express the following proposition combinations using symbolic notation. a) The girl is beautiful and smart. p q b) The girl is beautiful but not smart. p q c) The girl is neither beautiful nor smart. d) It is not true that the girl is ugly or not smart. ( p q) e) The girl is beautiful, or ugly and smart. p ( p q) f) That the girl is ugly as well as smart, is not true. ( p q) Erwin Sitompul Discrete Mathematics 1/17

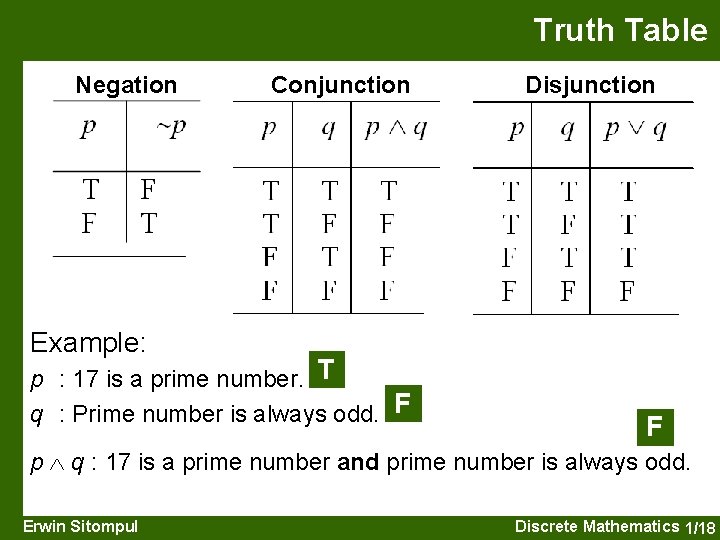
Truth Table Negation Conjunction Disjunction Example: p : 17 is a prime number. T q : Prime number is always odd. F F p q : 17 is a prime number and prime number is always odd. Erwin Sitompul Discrete Mathematics 1/18

Proposition Operation in Google Erwin Sitompul Discrete Mathematics 1/19

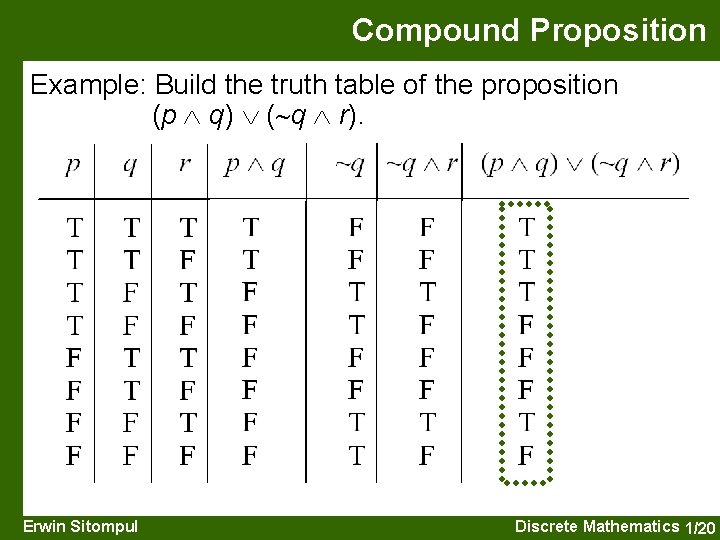
Compound Proposition Example: Build the truth table of the proposition (p q) ( q r). Erwin Sitompul Discrete Mathematics 1/20

Tautology and Contradiction Compound proposition which is always true for all cases is called tautology. Compound proposition which is always false for all cases is called contradiction. Example: p (p q) is a tautology Erwin Sitompul Discrete Mathematics 1/21

Tautology and Contradiction Example: (p q) is a contradiction Erwin Sitompul Discrete Mathematics 1/22

Equivalence of Compound Proposition Two compound proposition P(p, q, …) and Q(p, q, …) are said to be logically equivalent if they have identical truth table. Notation: P(p, q, …) Q(p, q, …) Example: De Morgan’s Law (p q) p q Erwin Sitompul Discrete Mathematics 1/23

Logical Laws Erwin Sitompul Discrete Mathematics 1/24

Logical Laws Erwin Sitompul Discrete Mathematics 1/25

Logical Equivalence Example: Show that p ~(p q) and p ~q are logically equivalent. p ~(p q ) p (~p ~q) (p ~p) (p ~q) T (p ~q) p ~q Erwin Sitompul (De Morgan’s Law) (Distributive Law) (Negation Law) (Identity Law) Discrete Mathematics 1/26

Logical Equivalence Example: Proof the truth of Absorption Law p (p q) p p (p q) (p F) (p q) p (F q) p F p Erwin Sitompul (Identity Law) (Distributive Law) (Domination Law) (Identity Law) Discrete Mathematics 1/27

Exclusive Disjunction The word “or” can be used in two ways in logical operation: 1. Inclusive or “or” in the sense “p or q or either” Example: “The required IE engineer must master Auto. CAD or Solid. Works”. 2. Exclusive or “or” in the sense “p or q but not both” Example: “He is punished with 5 years prison plus Rp 500 millions fine or additional 3 months prison. Erwin Sitompul Discrete Mathematics 1/28

Exclusive Disjunction Logical operator for exclusive disjunction is xor, with the notation . Erwin Sitompul Discrete Mathematics 1/29

Conditional Proposition Conditional proposition is also called implication. • Form: “If p, then q” • Notation: p q • Proposition p is called hypothesis, antecedent, premise, or condition. • Proposition q is called conclusion or consequence. Erwin Sitompul Discrete Mathematics 1/30

Conditional Proposition Example: § If I pass the exams, then I will get presents from my parents. § If the temperature reaches 80 C, then the alarm will buzz. § If you have not enrolled properly, then your name will not be printed on the attendance list. Truth table for implication: Erwin Sitompul Discrete Mathematics 1/31

Conditional Proposition Lecturer: “If your final exam grade is 80 or more, then you will get an A for this subject. ” Case 1: Your final exam grade is higher than 80 (true hypothesis) and you get an A for the subject (true conclusion). The lecturer tells the truth. TRUE Case 2: Your final exam grade is higher than 80 (true hypothesis) but you do not get an A (false conclusion). The lecturer tells a lie. FALSE Case 3: Your final exam grade is lower than 80 (false hypothesis) and you get an A (true conclusion). The lecturer cannot be said to be wrong or telling a lie. Maybe he/she see your extra efforts and high motivation and thus without any doubt to give you an A. TRUE Case 4: Your final exam grade is lower than 80 (false hypothesis) and you do not get an A (false conclusion). The lecturer tells the truth. TRUE Erwin Sitompul Discrete Mathematics 1/32

Conditional Proposition Various ways to express implication p q: § § § § § If p, then q. If p, q. p implies/causes q. q if p. p only if q. p is the sufficient condition for q. p is sufficient for q. q is the necessary condition for p. q is necessary for p. q whenever p. Erwin Sitompul Discrete Mathematics 1/33

Conditional Proposition Example: Implication in various forms § If today is rainy, then the flowers will grow well. § If the gas pedal is pressed deeper, the car moves fast. § Ice melted in north and south pole causes the increase of sea level. § He is willing to go if he is given travel allowance. § Ahmad can take Factory Layout only if he already passed Discrete Mathematics. § The sufficient condition for a gas station to explode is small cigarette sparks. § The necessary condition for Indonesia to win the World. Cup. TM is by hiring a famous foreign trainer. !! Erwin Sitompul Convert all propositions above into “If p then q” Discrete Mathematics 1/34

Conditional Proposition Example: Show that p q is logically equivalent with ~p q. “If p, then q” “Not p or q” Example: Determine the negation of p q. ~(p q) ~(~p) ~q p ~q Erwin Sitompul Discrete Mathematics 1/35

Conditional Propositions Express the following proposition combinations using symbolic notation. a) You can access the internet from campus only if you a (s ¬g) are a student or you are not a university guest. b) You cannot ride the roller coaster if you are under 100 cm tall unless you are older than 16 years old. (u ¬o) ¬r Erwin Sitompul Discrete Mathematics 1/36

Homework 1 Two merchants publish new marketing campaign to attract more customers. The first merchant launches a motto “Good stuffs are not cheap”, while the second merchants says “Cheap stuffs is not good”. a) Examine whether both mottos tell the same message or not. b) In your opinion, which motto is better? Erwin Sitompul Discrete Mathematics 1/37

Homework 1 New Examine whether both following statements are logically equivalent or not. S 1: Excellent physical condition is the necessary condition to become a soldier. S 2: If someone does not have excellent physical condition, then he cannot become a soldier. Erwin Sitompul Discrete Mathematics 1/38