Propositional Logic 1 Propositional Language 2 Translations 3






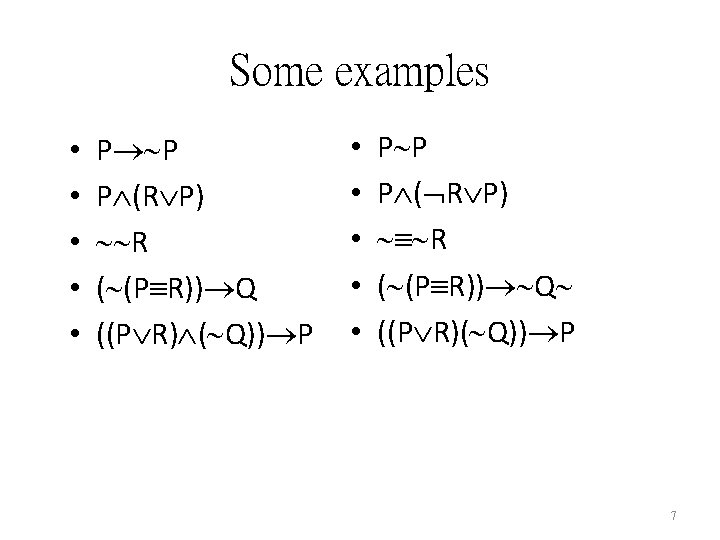









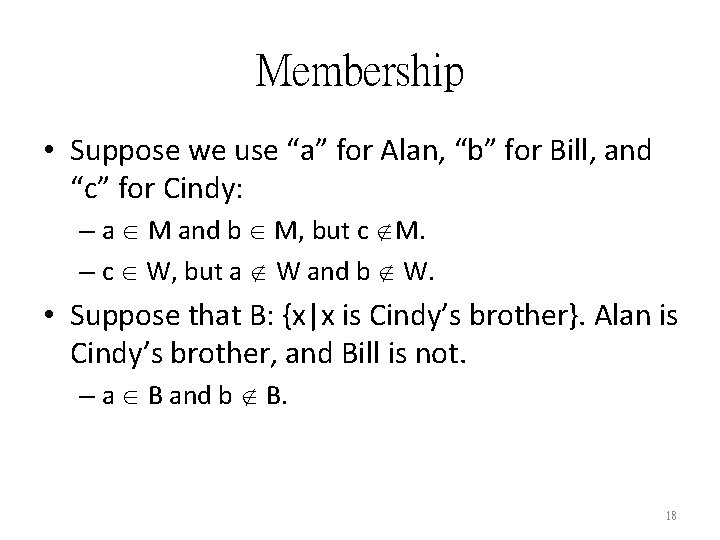






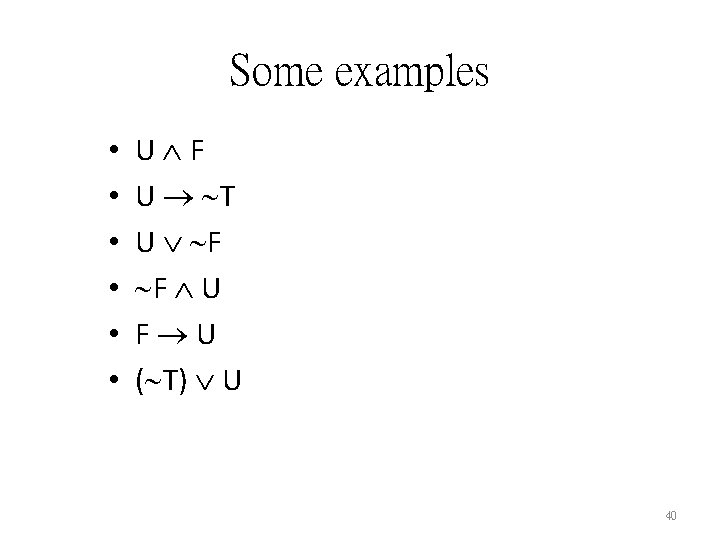

























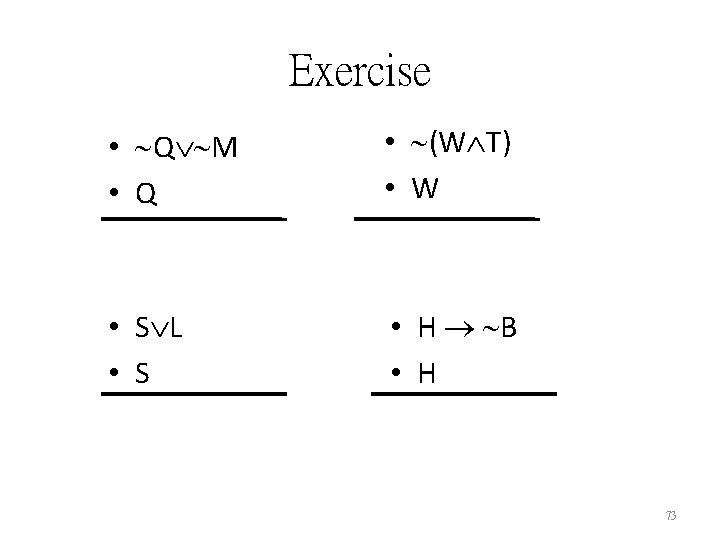
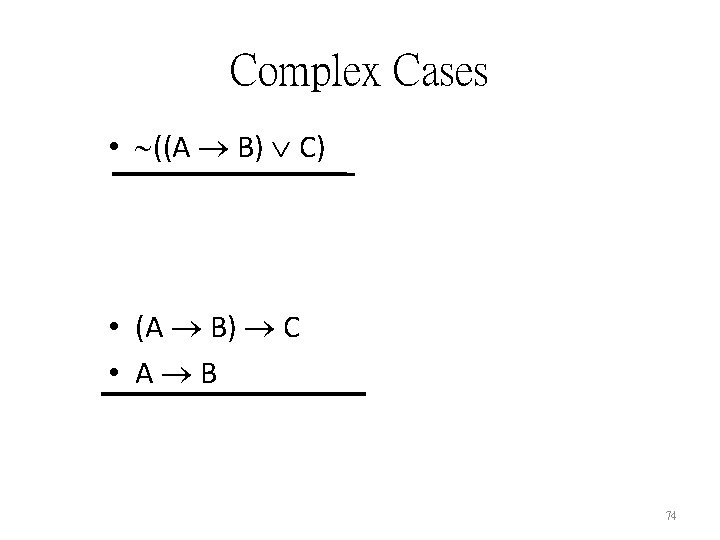


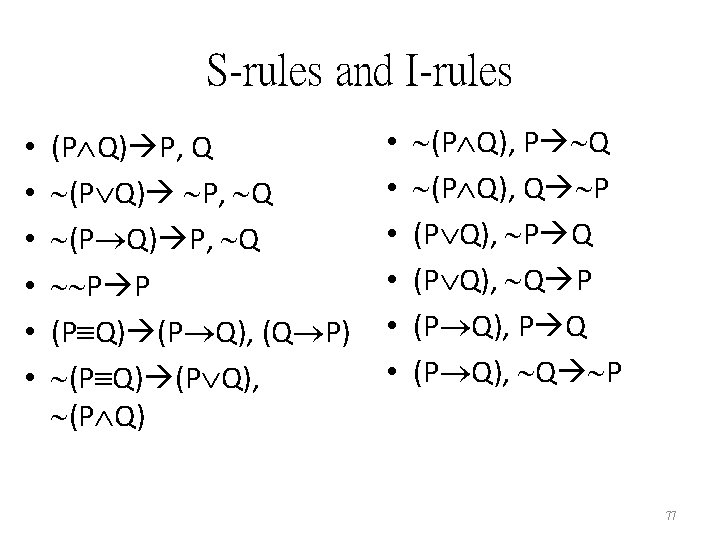



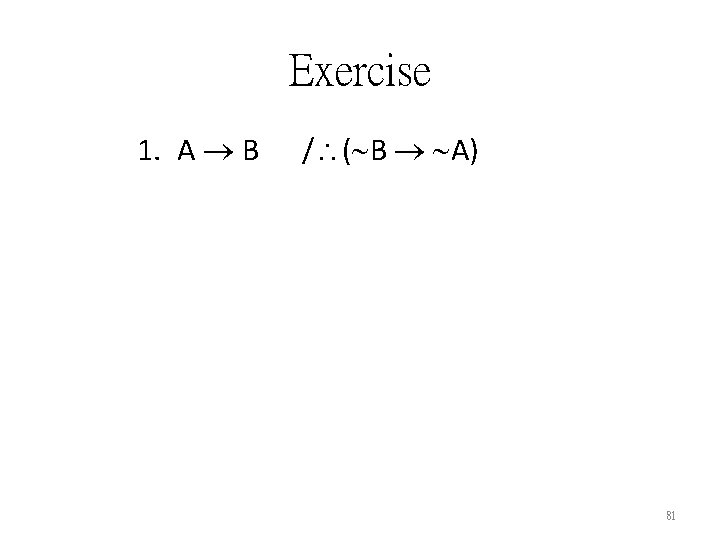


![Translation 1. [we had an absolute proof of God’s existence] [our will would be Translation 1. [we had an absolute proof of God’s existence] [our will would be](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-84.jpg)





![1. [racism is clearly wrong] [either it’s factually clear that all races have equal 1. [racism is clearly wrong] [either it’s factually clear that all races have equal](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-90.jpg)






![1. [the butler was at the party] [he fixed the drinks and poisoned the 1. [the butler was at the party] [he fixed the drinks and poisoned the](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-97.jpg)
![1. A [{he fixed the drinks} {poisoned the deceased}] 2. [the butler was at 1. A [{he fixed the drinks} {poisoned the deceased}] 2. [the butler was at](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-98.jpg)










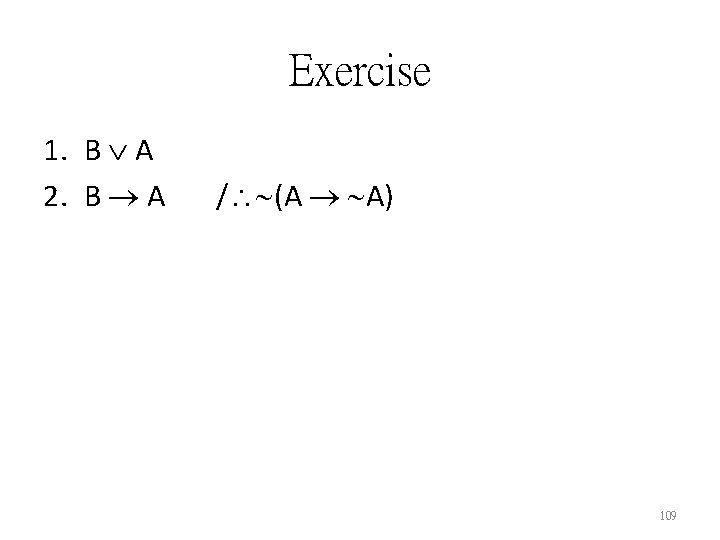
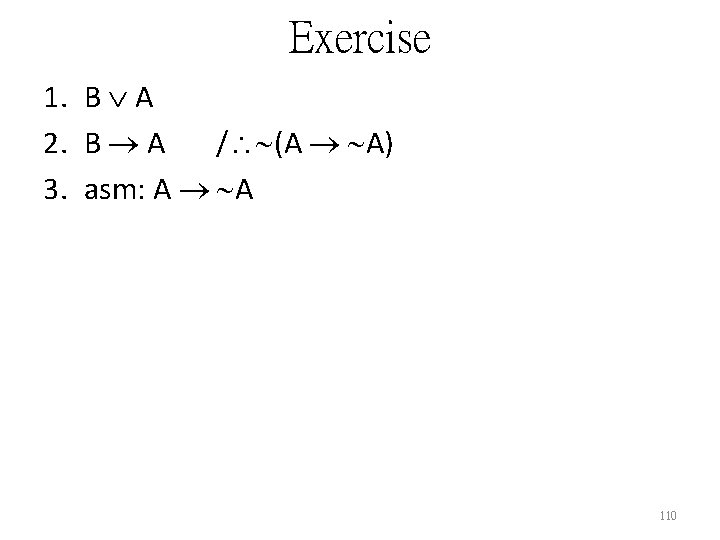



![1. [determinism is true and Dr. Freudlov correctly predicts what I will do] [if 1. [determinism is true and Dr. Freudlov correctly predicts what I will do] [if](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-114.jpg)
![1. [{determinism is true} {Dr. Freudlov correctly predicts what I will do}] [{she tells 1. [{determinism is true} {Dr. Freudlov correctly predicts what I will do}] [{she tells](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-115.jpg)
![1. [{determinism is true} {Dr. Freudlov correctly predicts what I will do}] [{she tells 1. [{determinism is true} {Dr. Freudlov correctly predicts what I will do}] [{she tells](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-116.jpg)
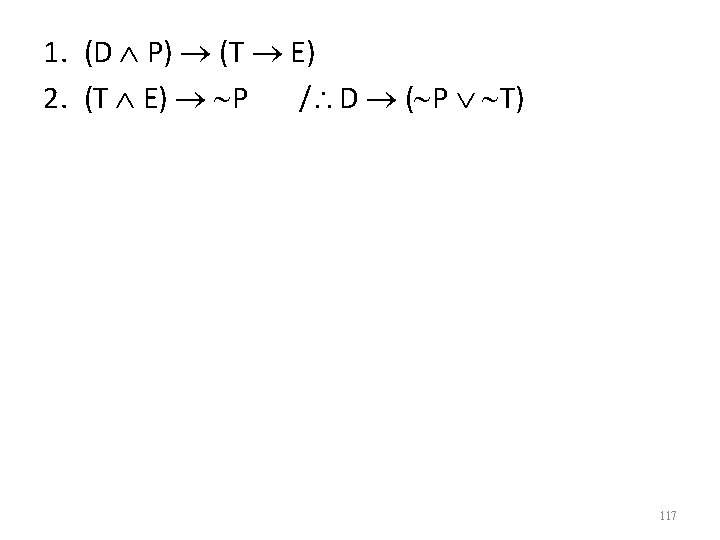























- Slides: 141

Propositional Logic 1. Propositional Language 2. Translations 3. Truth Tables 4. Propositional Proofs 5. Appendix: Model Theory 1

Introduction • Propositional logic studies arguments whose validity depends on “if-then, ” “and, ” “or, ” “not, ” and similar notions. • In the following, firstly we will introduce a formal language that sets up the framework of propositional logic, and then explain the relationship between this language and natural languages. • Secondly, we will introduce a simple model of it, i. e. the one made by truth-tables. • Finally, we will introduce inference rules and show to construct a proof. 2

1. Propositional Language PL • vocabulary • formation rules 3

Vocabulary • Logical constants: logical connectives – “ , ” and “. ” • Logical variables: propositional variables – P, Q, R…, and so on. (if necessary with subscripts appended—like ”P 1”) • Auxiliary Signs: brackets – “ (, ” and “). ” 4

The Function of Brackets • Consider the case in mathematics: – 2+3 5=? – Either (2+3) 5=25 or 2+(3 5)=17. • Similarly consider the following case: – What does “ P R” mean? – It means either that ( P) R or that (P R). • The function of brackets is to disambiguate the meaning of wffs (well-formed formula). 5

Formation Rules (i) Any capital letter is a well-formed formula. (ii) The result of prefixing any wff with “ ” is a wff. (iii) The result of joining any two wffs by “ , ” or “ ” and enclosing the result in parentheses is a wff. (iv) Only that which can be generated by the rules (i)-(iii) in a finite number of steps is a wff in PL. 6
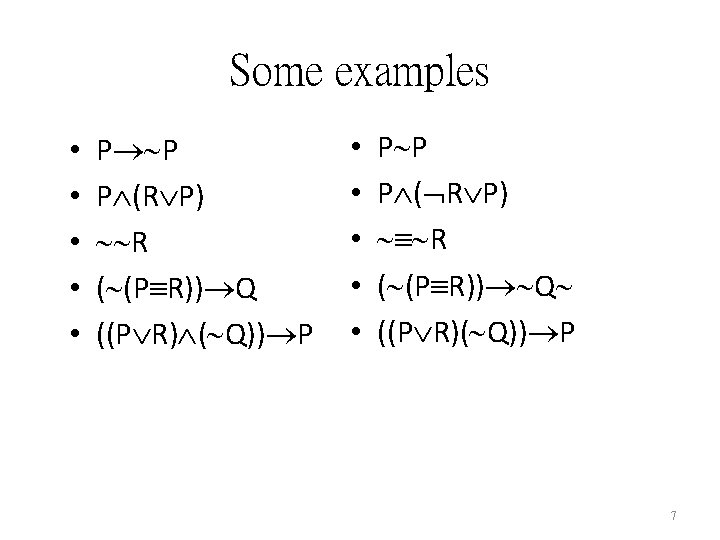
Some examples • • • P P P (R P) R ( (P R)) Q ((P R) ( Q)) P • • • P P P ( R P) R ( (P R)) Q ((P R)( Q)) P 7

Construction Tree (Top-Down) • For any wff in PL, we can construct a tree for it. • Ex. P P (iii, ) P (i) P (ii, ) P (i) 8

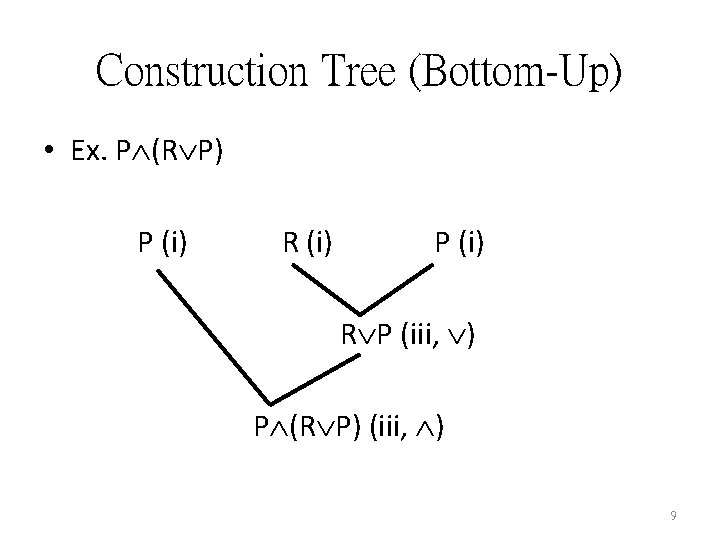
Construction Tree (Bottom-Up) • Ex. P (R P) P (i) R (i) P (i) R P (iii, ) P (R P) (iii, ) 9

Main Connectives • The main connective of a formula is at the top of the tree (Top-down)—at the bottom if bottom-up. • In another words, if the whole sentence was constituted at last by one connective, then we call this one as main connective of this sentence. • Note: the leaf of tree must be atomic. 10


2. Translations • As mentioned earlier, propositional logic studies arguments whose validity depends on “ifthen, ” “and, ” “or, ” “not, ” and similar notions. • It follows that PL must contain these notions in order to represent natural languages to certain degree. • In a way, we can translate arguments in natural languages into wffs in PL. 12

Connectives • • • “ ” stands for “not. ” “ ” stands for “and. ” (or “but, ” “though”) “ ” stands for “or. ” (inclusive-or) “ ” stands for “if-then. ” “ ” stands for “if and only if. ” 13

Some examples • It will rain tomorrow. • It will not rain tomorrow. • It will rain tomorrow and I will bring my umbrella. • If it rains tomorrow, I will bring my umbrella. • Either it rains tomorrow, or it will not rain. • It will rain heavily if and only if the sky will be covered with dark clouds. 14

More… • Not both Alan and Bill like to play baseball. • If Alan took this course and Bill dropped this course, I would take this course. • Only if Cindy took this course, I would take this course. • Not either Alan drops this course or Bill drops this course. 15

3. Truth Tables • Logical connectives are represented by some truth functions—by which we can calculate the truth table of each compound wff. • Before we introduce logical connectives, let’s see what a function is and what kind of function is called “truth functional. ” 16

Set • A set is a collection of entities (or objects). • The principle of extensionality: – A set is defined by the members it contains. • Ex. Suppose our domain is {Alan, Bill, Cindy} – M: {Alan, Bill} (M: {x|x is a man}) – W: {Cindy} (W: {x|x is a woman}) 17
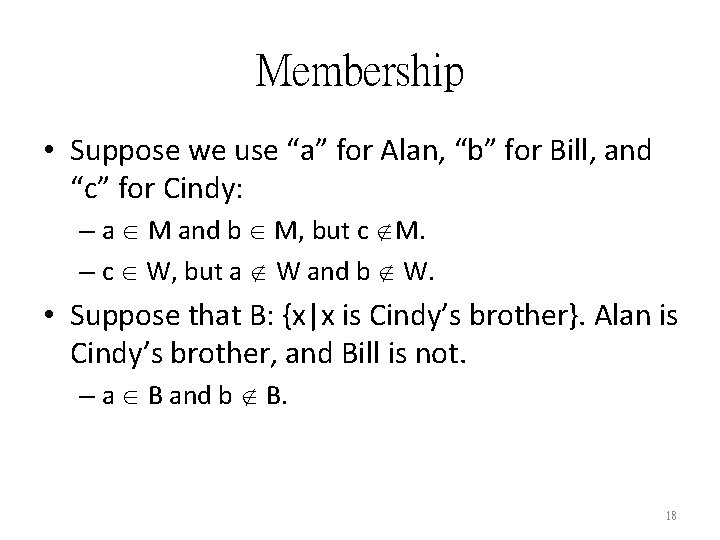
Membership • Suppose we use “a” for Alan, “b” for Bill, and “c” for Cindy: – a M and b M, but c M. – c W, but a W and b W. • Suppose that B: {x|x is Cindy’s brother}. Alan is Cindy’s brother, and Bill is not. – a B and b B. 18

Subset • If A is a subset of B, then if x A, then x B. –A B • If A is a proper subset of B, then if x A then x B and, for some y, such that y B and y A. –A B • Ex. – Given that M: {a, b} and B: {a}, we call B is a proper subset of M—symbolized as B M. 19

Intersection and Union • A B : {x x A and x B} • A B : {x x A or x B} • Ex. – {1, 2, 3} {2, 4, 6}={1, 2, 3, 4, 6} – {1, 2, 3} {2, 4, 6}={2} 20

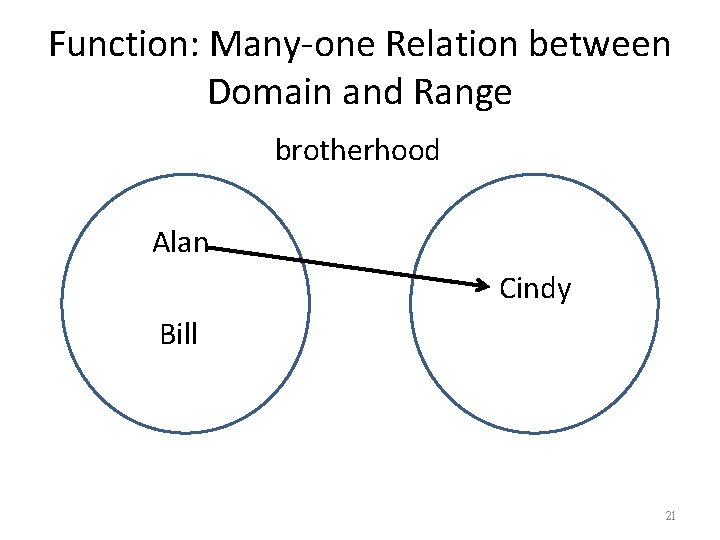
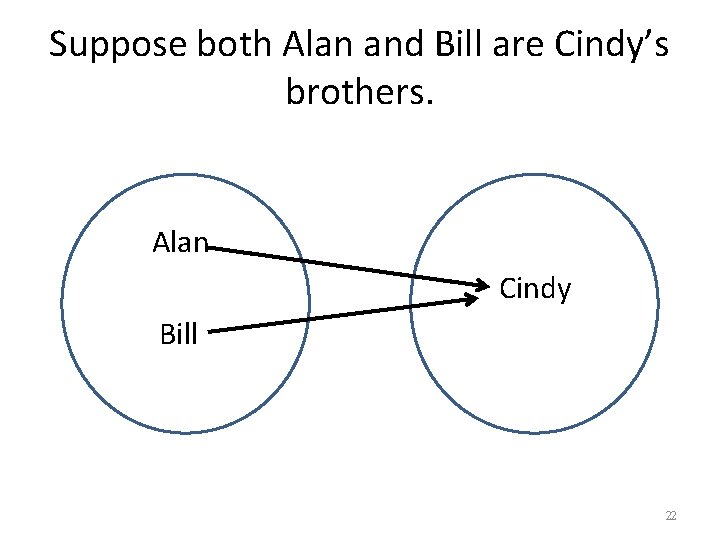
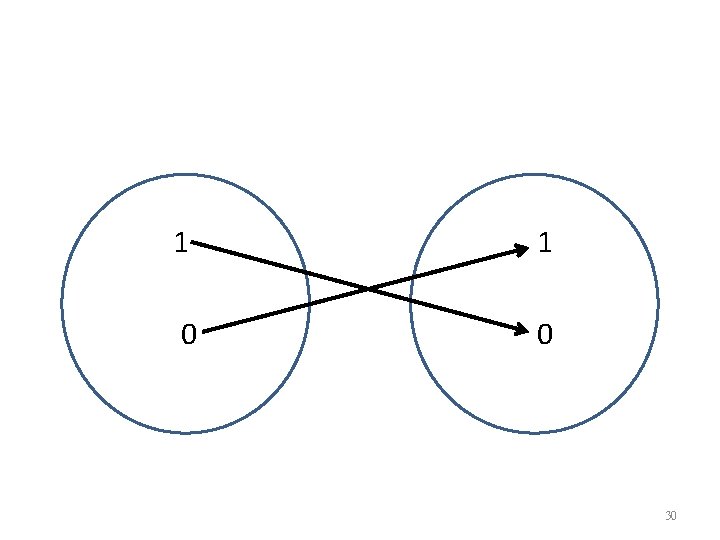
Function: Many-one Relation between Domain and Range brotherhood Alan Cindy Bill 21

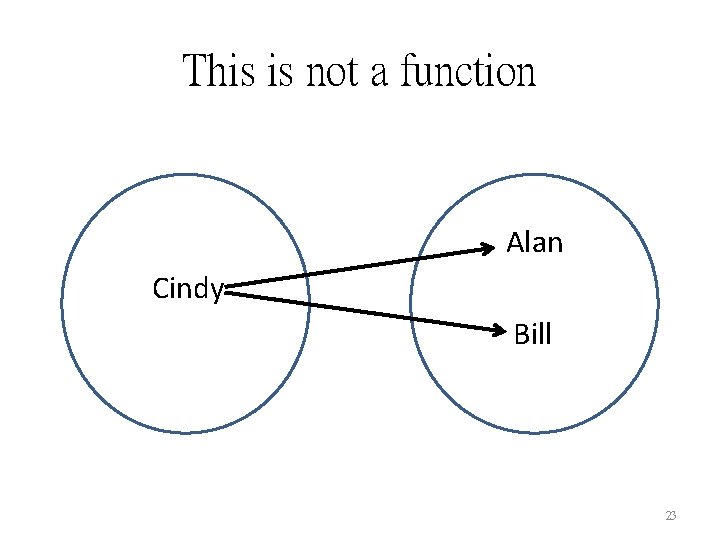
Suppose both Alan and Bill are Cindy’s brothers. Alan Cindy Bill 22

This is not a function Alan Cindy Bill 23

Function 1 1 0 0 24

Compound Function 1 1 1 0 0 0 25

1 1 1 0 0 0 26

1 1 1 0 0 0 27

1 1 1 0 0 0 28

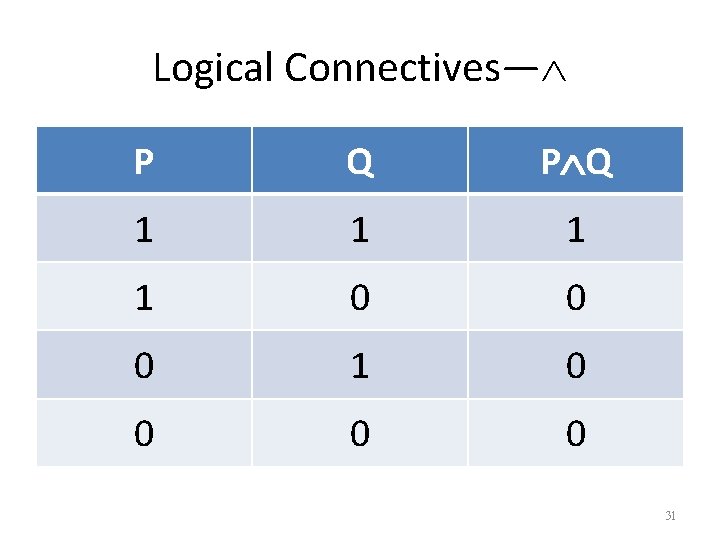
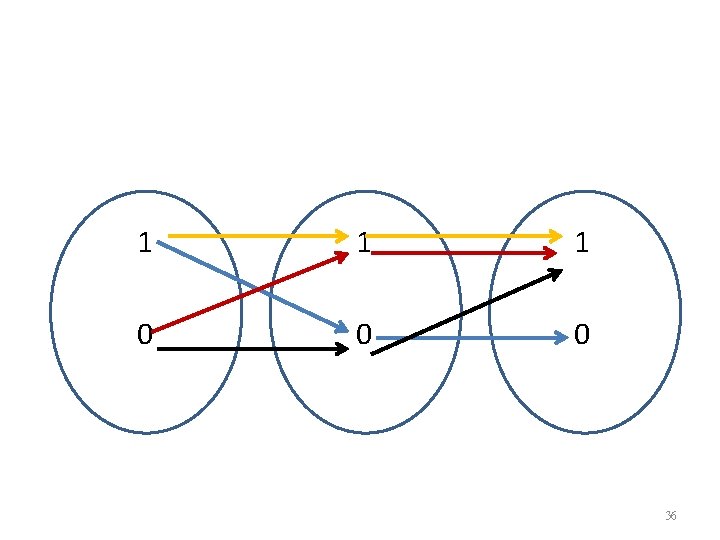
Logical Connectives— P P 1 0 0 1 29

1 1 0 0 30

Logical Connectives— P Q 1 1 0 0 0 1 0 0 31

1 1 1 0 0 0 32

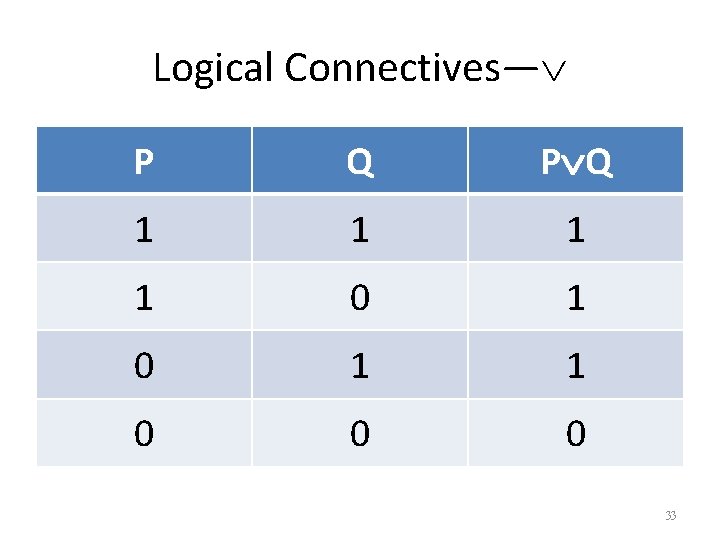
Logical Connectives— P Q 1 1 0 0 0 33

1 1 1 0 0 0 34

Logical Connectives— P Q 1 1 0 0 0 1 1 0 0 1 35

1 1 1 0 0 0 36

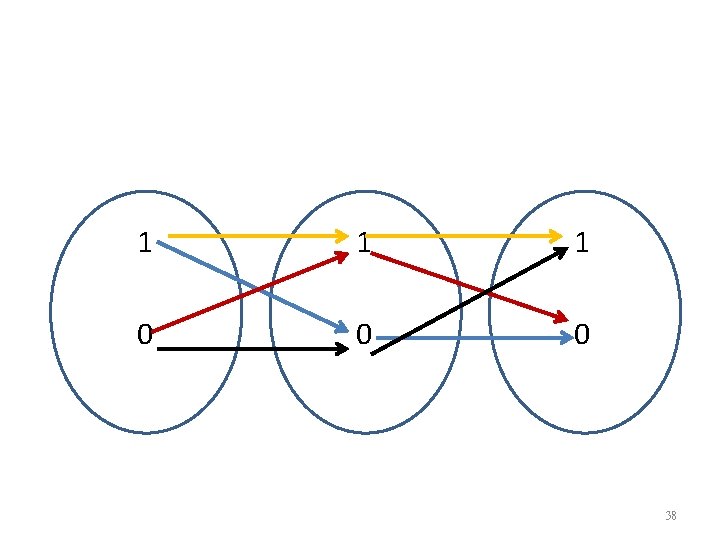
Logical Connectives— P Q 1 1 0 0 0 1 37

1 1 1 0 0 0 38

Truth Function • Connectives which give rise to sentences whose truth value depends only on the truth values of the connected sentences are said to be truth-functional. • Therefore, “not” ( ), “or” ( ), “and” ( ), “ifthen” ( ), and “if and only if” ( ) are truthfunctional. 39
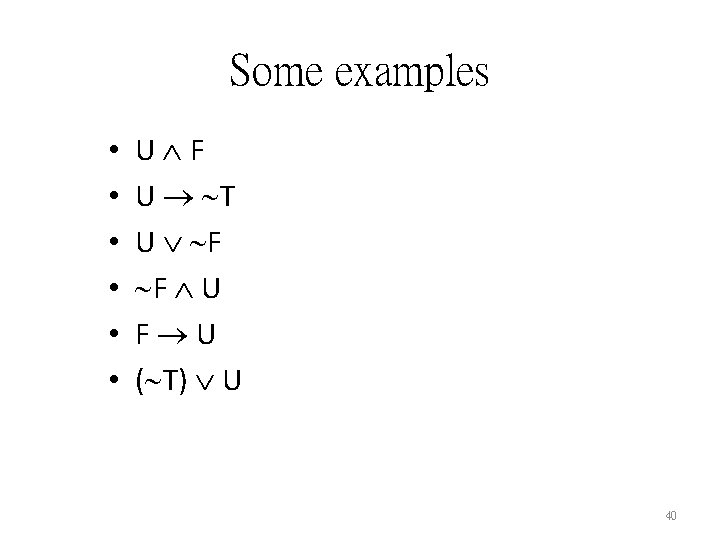
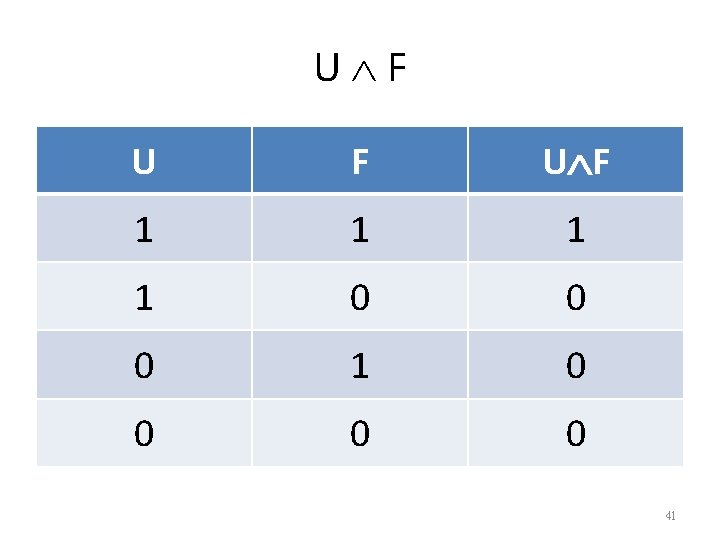
Some examples • • • U F U T U F F U F U ( T) U 40

U F U F 1 1 0 0 0 1 0 0 41

U T U T 1 1 0 0 1 1 0 1 0 0 1 1 42

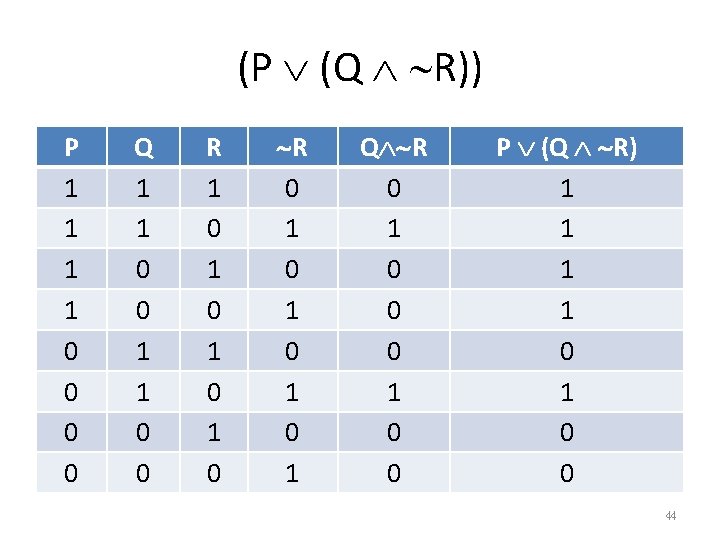
Complex Truth Tables • • • (P (Q R)) ((P Q) R) ((P Q) R) (P (Q R)) 43

(P (Q R)) P 1 1 0 0 Q 1 1 0 0 R 1 0 1 0 R 0 1 0 1 Q R 0 1 0 0 P (Q R) 1 1 0 1 0 0 44

Functional Completeness • A system of connectives can express all truth functions is said to be functionally complete. • Ex. Define “ ” by “ ” and “. ” • Actually, we can use “ ” and “ ” to represent others, and we call these two functions functionally complete. 45

• Can you find another system of connectives which is also functionally complete? 46

The Truth-table Test • Recall how valid and invalid are defined for arguments: – VALID = no possible case has premises all true and conclusion false. – INVALID = some possible case has premises all true and conclusion false. • Now, we can use the truth-table test on a propositional argument. 47

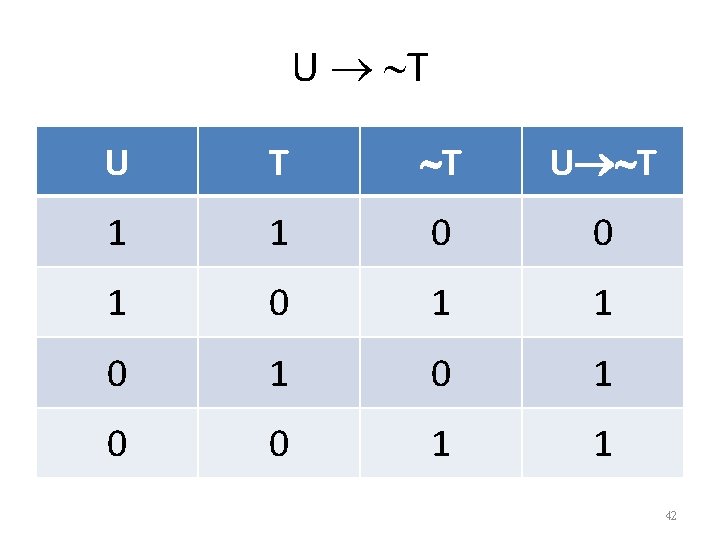
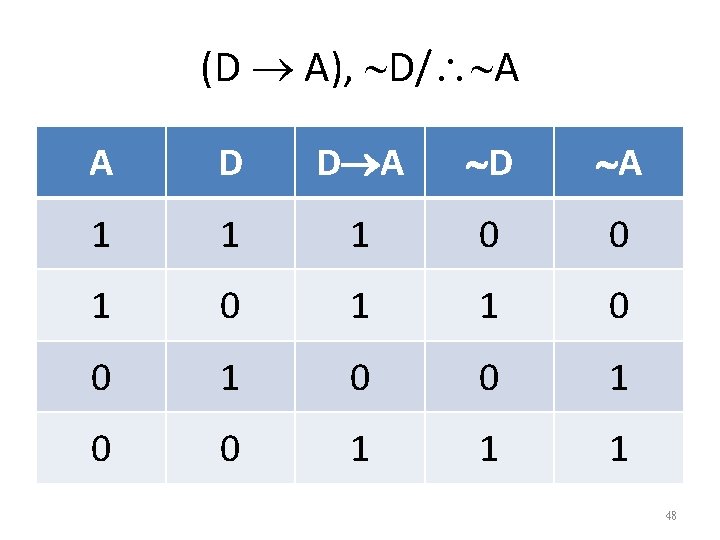
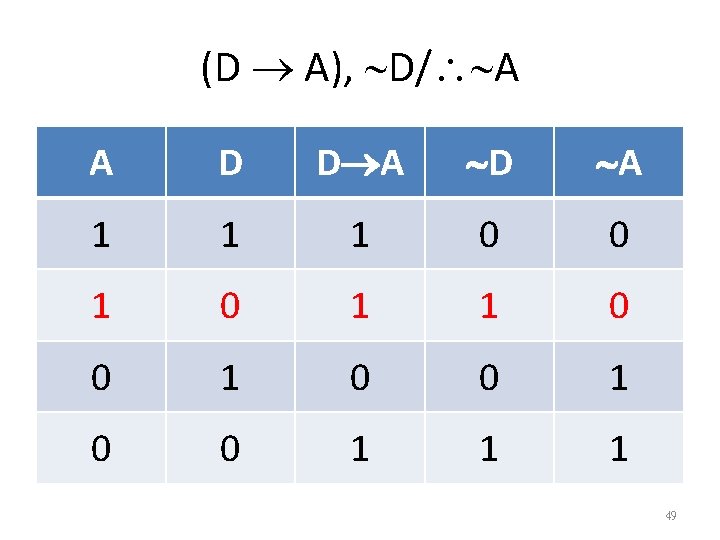
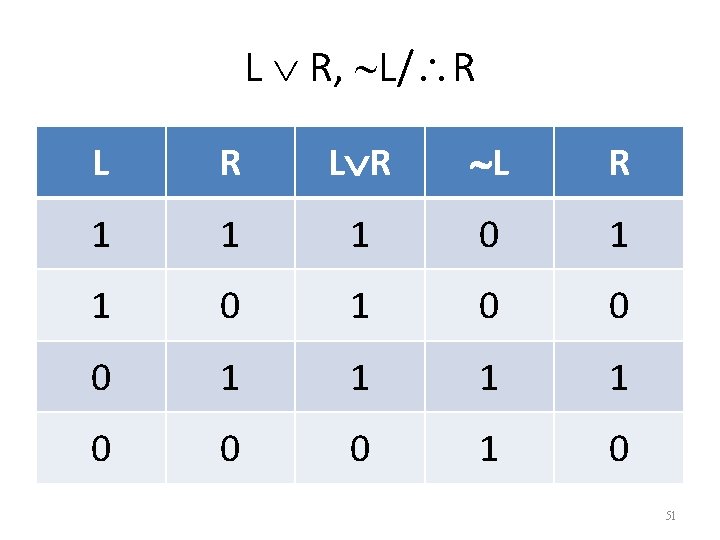
(D A), D/ A A D D A D A 1 1 1 0 0 1 0 0 1 1 1 48

(D A), D/ A A D D A D A 1 1 1 0 0 1 0 0 1 1 1 49

More example • It is in your left hand or your right hand. • It is not in your left hand. • It is in your right hand. (L: it is in your left hand; R: it is in your right hand) • L R • L • R 50

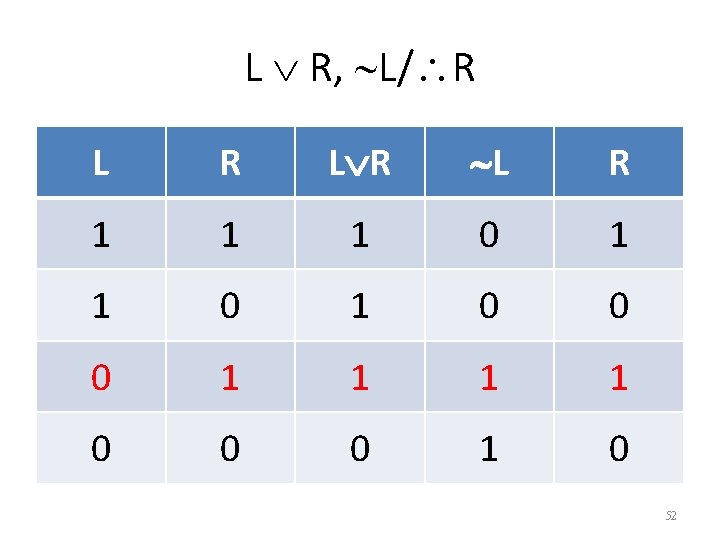
L R, L/ R L R 1 1 1 0 1 0 0 0 1 0 51

L R, L/ R L R 1 1 1 0 1 0 0 0 1 0 52

The Truth-assignment Test • Set each premise to 1 and the conclusion 0. • Figure out the truth value of as many letters as possible. • The argument is VALID if and only if no possible way to assign 1 and 0 to the letters will keep the premises all 1 and conclusion 0. 53

L R, L/ R • Step 1: we set each premise to 1 and the conclusion 0. –L R=1 – L = 1 –R=0 54

L R, L/ R • Step 2: since premise 2 has L = 1, we know that L = 0. – 0 R=1 – 0 = 1 –R=0 55

L R, L/ R • Step 3: since the conclusion has R = 0, – 0 0=1 – 0 = 1 – 0=0 56

L R, L/ R • Step 4: – 0 0=1 – 0 = 1 – 0=0 • But the premise 1 cannot be true. So we cannot have true premises and a false conclusion. 57

Some examples • If existence is a perfection and God by definition has all perfection, then God by definition must exist. • God by definition has all perfections. • God by definition must exist. 58

• If Newton’s gravitational theory is correct and there is no undiscovered planet near Uranus, then the orbit of Uranus would be such-andsuch. • Newton’s gravitational theory is correct. • The orbit of Uranus is not such-and-such. • There is an undiscovered planet near Uranus. 59

Idiomatic Arguments • Our arguments so far have been phrased in a clear premise-conclusion format. • Unfortunately, real-life arguments are seldom so neat and clean. • Instead we often find convoluted wording or extraneous material. 60

For example • Socrates must be mortal. After all, he is human. And if he is human, he is mortal. • Socrates is human. • If Socrates is human, he is mortal. • Socrates is mortal. 61

A Guide • These often indicate premises: – Because, for, since, after all… – I assume that, as we know… – For these reasons… • These often indicate conclusions: – Hence, thus, so, therefore… – It must be, it can’t be… – This proves (or shows) that… 62

Some examples • Knowledge can’t be sensation. If it were, then we couldn’t know something that we aren’t presently sensing. • Taking the exam is a sufficient condition for getting an A. You didn’t take the exam. This means you don’t get an A. 63

4. Propositional Proofs • We will learn some inference rules, which state that certain formulas can be derived from certain other formulas. • Most of these rules reflect common forms of reasoning. • These rules also provide the building blocks formal proofs—formal proofs reduce a complex arguments to a series of small steps, each based on an inference rule. 64

S-Rules (E-Rules) • The S-rules are used to simplify statements. In other words, we can infer statement without certain logical connective from those containing logical connective—to infer a simplified formula. • So we may also call these rules E-rules—”E” for “eliminate. ” • As one may notice, each connective will have one S-rule (E-rule) respectively. 65

AND—E-rule for • P Q • P • P Q • Q • Alan is hungry and so is Bill. • Therefore, Alan is hungry. • Therefore, Bill is hungry. 66

NOR—E-rule for • (P Q) • P • (P Q) • Q • Alan is neither in school nor at home. • Therefore, Alan is not in school. • Therefore, Alan is not at home. 67

NIF—E-rule for • (P Q) • P • (P Q) • Q • It is not the case that if Alan gets sick, he will be happier. • Therefore, Alan gets sick. • Therefore, Alan is not happier. 68

I-Rules • The I-rules are used to infer a conclusion from premises. 69

CS—I-rule for • (P Q) • Q • P • (P Q) • P • Q • Alan is not both hungry and thirsty. • Alan is hungry. • Therefore, Alan is not thirsty. 70

DS—I-rule for • (P Q) • P • Q • (P Q) • Q • P • Alan is either angry or sad about what happened to Bill. • Alan is not angry. • Therefore, Alan is sad. 71

MP—I-rule for • (P Q) • P • Q • (P Q) • Q • P • If Alan gets sick, he will stay at home. • Alan gets sick. • Therefore, Alan stays at home. • (Alan doesn’t not stay at home. Therefore, Alan didn’t get sick. ) 72
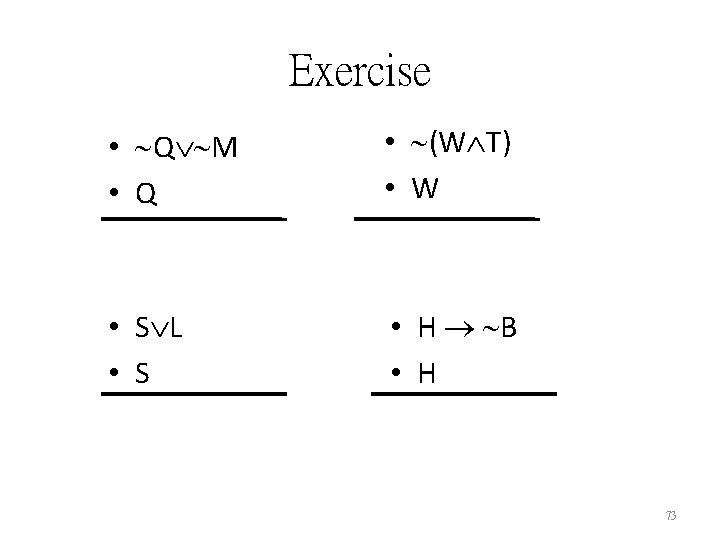
Exercise • Q M • Q • (W T) • W • S L • S • H B • H 73
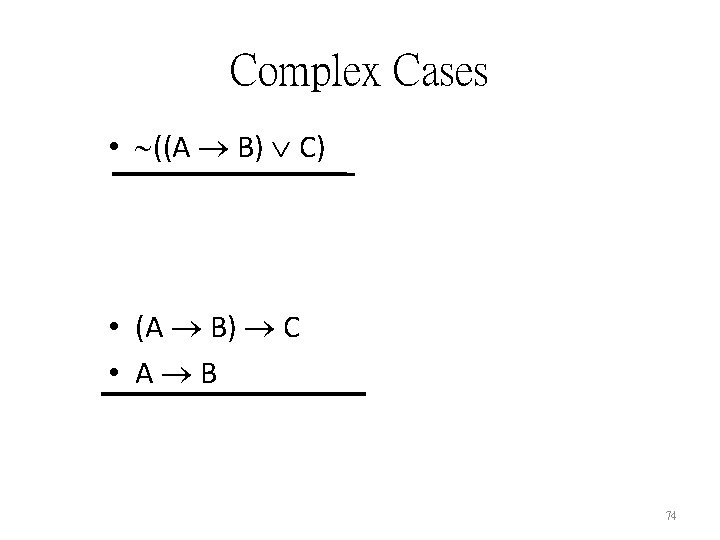
Complex Cases • ((A B) C) • (A B) C • A B 74

Formal Proofs • Formal proofs are a convenient way to test arguments of various systems and, in addition, help to develop reasoning skills. • A formal proof breaks a complicated argument into a series of small steps, each based on our Srules or I-rules. 75

Indirect Proof Strategy (RAA) • First Step: – Block off the conclusion and add “asm: ” (for “assume”) followed by the conclusion’s simpler contradictory. • Second Step: – Go through the complex wffs, to which we can apply S-rules or I-rules. • Third Step: – To find a contradiction through reasoning, and apply RAA and derive the original conclusion. 76
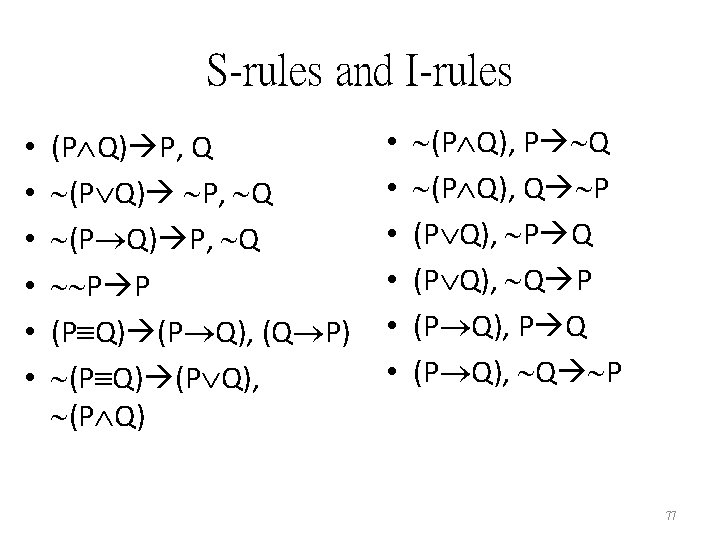
S-rules and I-rules • • • (P Q) P, Q (P Q) P, Q (P Q) P, Q P P (P Q), (Q P) (P Q), (P Q) • • • (P Q), P Q (P Q), Q P (P Q), P Q (P Q), Q P (P Q), P Q (P Q), Q P 77

For example—First Step 1. 2. 3. 4. 5. T T (B M) M H H / B asm: B 78

For example—Second Step 1. 2. 3. 4. 5. 6. 7. 8. T T (B M) M H H / B asm: B B M {from 1 and 2, MP} M {from 5 and 6, CS} H {from 3 and 7, MP} 79

For example—Third Step 1. 2. 3. 4. 5. 6. 7. 8. 9. T T (B M) M H H / B asm: B B M {from 1 and 2, MP} M {from 5 and 6, CS} H {from 3 and 7, MP} B {from 5; 4 contradicts 8, RAA} 80
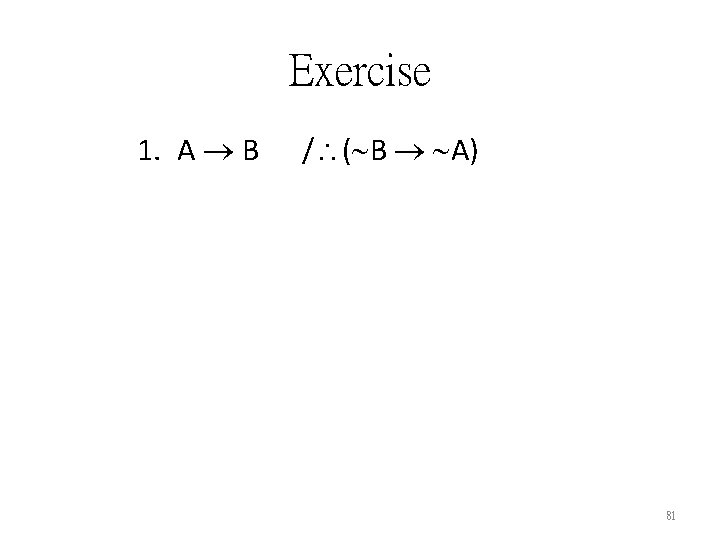
Exercise 1. A B / ( B A) 81

Exercise 1. A / A B 82

Exercise with Translation 1. If we had an absolute proof of God’s existence, then our will would be irresistibly attracted to do right. 2. If our will were irresistibly attracted to do right, then we would have no free will. 3. Therefore, if we have free will, then we have no absolute proof of God’s existence. 83
![Translation 1 we had an absolute proof of Gods existence our will would be Translation 1. [we had an absolute proof of God’s existence] [our will would be](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-84.jpg)
Translation 1. [we had an absolute proof of God’s existence] [our will would be irresistibly attracted to do right] 2. [our will were irresistibly attracted to do right] [we would have no free will] 3. [we have free will] [we have no absolute proof of God’s existence] 84

Translation 1. P I 2. I F / F P 85

Proof 1. P I 2. I F / F P 3. asm: (F P) First Step! 86

Proof Second Step! 1. 2. 3. 4. 5. 6. 7. 8. P I I F / F P asm: (F P) F {from 3, NIF} P {from 3, NIF} P {from 5, DN} I {from 1 and 6, MP} F {from 2 and 7, MP} 87

Proof 1. 2. 3. 4. 5. 6. 7. 8. 9. P I I F / F P asm: (F P) F {from 3, NIF} P {from 3, NIF} Third P {from 5, DN} Step! I {from 1 and 6, MP} F {from 2 and 7, MP} F P {from 3; 4 contradicts 8, RAA} 88

1. If racism is clearly wrong, then either it’s factually clear that all races have equal abilities or it’s morally clear that similar interests of all beings ought to be given equal consideration. 2. It is not factually clear that all races have equal abilities. 3. If it’s morally clear that similar interests of all beings ought to be given equal consideration, then similar interests of animals and humans ought to be given equal consideration. 4. Therefore, if racism is clearly wrong, then similar interests of animals and humans ought to be given equal consideration. 89
![1 racism is clearly wrong either its factually clear that all races have equal 1. [racism is clearly wrong] [either it’s factually clear that all races have equal](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-90.jpg)
1. [racism is clearly wrong] [either it’s factually clear that all races have equal abilities or it’s morally clear that similar interests of all beings ought to be given equal consideration] 2. [it is factually clear that all races have equal abilities] 3. [it’s morally clear that similar interests of all beings ought to be given equal consideration] [similar interests of animals and humans ought to be given equal consideration] 4. [racism is clearly wrong] [similar interests of animals and humans ought to be given equal consideration] 90

1. W [{it’s factually clear that all races have equal abilities} {it’s morally clear that similar interests of all beings ought to be given equal consideration}] 2. [it is factually clear that all races have equal abilities] 3. [it’s morally clear that similar interests of all beings ought to be given equal consideration] [similar interests of animals and humans ought to be given equal consideration] 4. W [similar interests of animals and humans ought to be given equal consideration] 91

1. W (F M) 2. F 3. M A / W A 92

1. 2. 3. 4. W (F M) F M A / W A asm: (W A) 93

1. 2. 3. 4. 5. 6. 7. 8. 9. W (F M) F M A / W A asm: (W A) W {from 4, NIF} A {from 4, NIF} F M {from 1 and 5, MP} M {from 2 and 7, DS} A {from 3 and 8, MP} 94

1. W (F M) 2. F 3. M A / W A 4. asm: (W A) 5. W {from 4, NIF} 6. A {from 4, NIF} 7. F M {from 1 and 5, MP} 8. M {from 2 and 7, DS} 9. A {from 3 and 8, MP} 10. W A {from 4; 6 contradicts 9, RAA} 95

Harder Proofs 1. If the butler was at the party, then he fixed the drinks and poisoned the deceased. 2. If the butler was not at the party, then the deceased would have seen him leave the mansion and would have reported this. 3. The deceased did not reported this. 4. Therefore, the butler poisoned the deceased. 96
![1 the butler was at the party he fixed the drinks and poisoned the 1. [the butler was at the party] [he fixed the drinks and poisoned the](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-97.jpg)
1. [the butler was at the party] [he fixed the drinks and poisoned the deceased] 2. [the butler was not at the party] [the deceased would have seen him leave the mansion and would have reported this] 3. [The deceased did reported this] 4. [the butler poisoned the deceased] 97
![1 A he fixed the drinks poisoned the deceased 2 the butler was at 1. A [{he fixed the drinks} {poisoned the deceased}] 2. [the butler was at](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-98.jpg)
1. A [{he fixed the drinks} {poisoned the deceased}] 2. [the butler was at the party] [{the deceased would have seen him leave the mansion} {would have reported this}] 3. [The deceased did reported this] 4. [the butler poisoned the deceased] 98

1. 2. 3. 4. 5. A (F P) A (S R) R / P asm: P ? 99

Strategy Expanded • Make another assumption when you’re stuck. – Make an assumption that breaks a complex wff. 100

1. 2. 3. 4. 5. A (F P) Pick a complex wff A (S R) (1 or 2), and pick R / P left or right side, and asm: P assume it or its asm: A {break 1} negation! 101

1. 2. 3. 4. 5. 6. 7. 8. A (F P) A (S R) R / P asm: A {break 1} S R {from 2 and 5, MP} S {from 6, AND} R {from 6, AND} 102

1. 2. 3. 4. 5. 6. 7. 8. 9. A (F P) A (S R) R / P asm: A {break 1} S R {from 2 and 5, MP} S {from 6, AND} R {from 6, AND} A {from 5; 3 contradicts 8, RAA} 103

1. A (F P) 2. A (S R) 3. R / P 4. asm: P 5. asm: A {break 1} 6. S R {from 2 and 5, MP} 7. S {from 6, AND} 8. R {from 6, AND} 9. A {from 5; 3 contradicts 8, RAA} 10. F P {from 1 and 9, MP} 11. P {from 10, AND} 104

1. A (F P) 2. A (S R) 3. R / P 4. asm: P 5. asm: A {break 1} 6. S R {from 2 and 5, MP} 7. S {from 6, AND} 8. R {from 6, AND} 9. A {from 5; 3 contradicts 8, RAA} 10. F P {from 1 and 9, MP} 11. P {from 10, AND} 12. P {from 4; 4 contradicts 11, RAA} 105

Final Proof Strategy • First Step: (START) – Add “asm: ” followed by the conclusion’s simpler contradictory. • Second Step: (S&I) – Apply S-rules and I-rules to the complex wffs: • If you get a contradiction, then go to the Third Step. • If you can’t derive anything further but there is a complex wff, then go to the Fourth Step. • If you can’t derive anything further and every complex wff are used, then go to the Fifth Step. • Third Step: (RAA) – Apply the RAA rule. • Fourth Step: (ASSUME) • Fifth Step: (REFUTE—Invalid Argument) 106

Final Proof Strategy • Fourth Step: (ASSUME) – Pick a complex wff (having one of these forms: “ (A B), ” “A B, ” or “A B. ”). – Assume one side or its negation, and then go to Second Step. • Fifth Step: (REFUTE—Invalid Argument) – Construct a refutation box containing any simple wffs. – Assign each wff 1 or 0, by which we can show this argument is invalid (all premises true and conclusion false). 107

Final Proof Strategy • First Step: (START) – Add “asm: ” followed by the conclusion’s simpler contradictory. • Second Step: (S&I) – Apply S-rules and I-rules to the complex wffs: • If you get a contradiction, then go to the Third Step. • If you can’t derive anything further but there is a complex wff, then go to the Fourth Step. • If you can’t derive anything further and every complex wff are used, then go to the Fifth Step. • Third Step: (RAA) – Apply the RAA rule. • Fourth Step: (ASSUME) – Pick a complex wff (having one of these forms: “ (A B), ” “A B, ” or “A B. ”). – Assume one side or its negation, and then go to Second Step. • Fifth Step: (REFUTE—Invalid Argument) – Construct a refutation box containing any simple wffs. – Assign each wff 1 or 0, by which we can show this argument is invalid (all premises true and conclusion false). 108
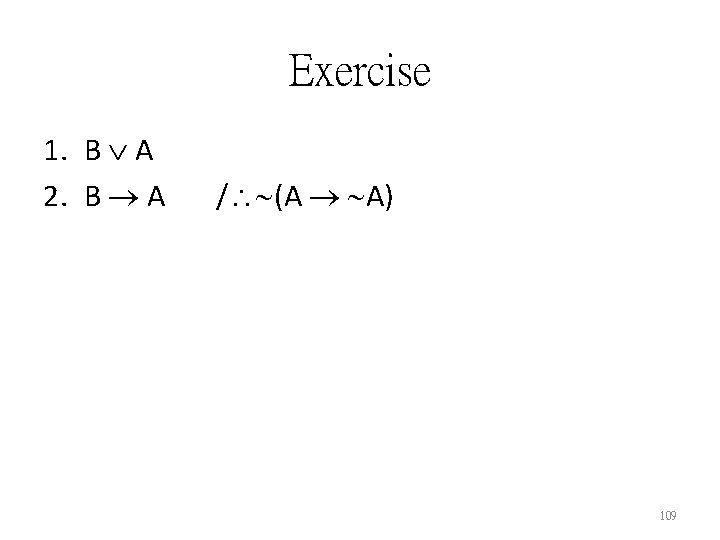
Exercise 1. B A 2. B A / (A A) 109
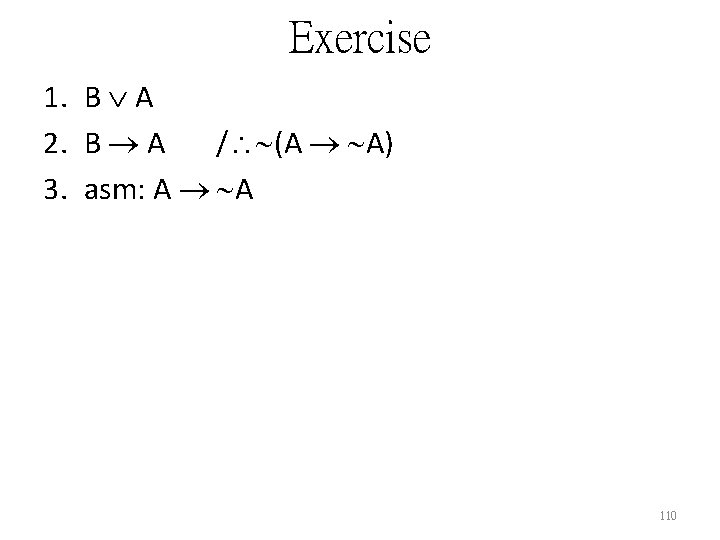
Exercise 1. B A 2. B A / (A A) 3. asm: A A 110

Exercise 1. 2. 3. 4. 5. 6. 7. B A / (A A) asm: A A asm: B {break 1} A {from 2 and 4, MP} A {from 3 and 5, MP} B {from 4; 5 contradicts 6, RAA} 111

Exercise 1. B A 2. B A / (A A) 3. asm: A A 4. asm: B {break 1} 5. A {from 2 and 4, MP} 6. A {from 3 and 5, MP} 7. B {from 4; 5 contradicts 6, RAA} 8. A {from 1 and 7, DS} 9. A {from 3 and 8, MP} 10. (A A){from 3; 8 contradicts 9, RAA} 112

Exercise with Translation 1. If determinism is true and Dr. Freudlov correctly predicts what I will do, then if she tells me her prediction I’ll do something else. 2. If Dr. Freudlov tells me her prediction and yet I’ll do something else, then Dr. Freudlov doesn’t correctly predict what I’ll do. 3. Therefore, if determinism is true, then Dr. Freudlov doesn’t correctly predict what I’ll do or else she won’t tell me her prediction. 113
![1 determinism is true and Dr Freudlov correctly predicts what I will do if 1. [determinism is true and Dr. Freudlov correctly predicts what I will do] [if](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-114.jpg)
1. [determinism is true and Dr. Freudlov correctly predicts what I will do] [if she tells me her prediction I’ll do something else] 2. [Dr. Freudlov tells me her prediction and yet I’ll do something else] [Dr. Freudlov doesn’t correctly predict what I’ll do] 3. [determinism is true] [Dr. Freudlov doesn’t correctly predict what I’ll do or else she won’t tell me her prediction] 114
![1 determinism is true Dr Freudlov correctly predicts what I will do she tells 1. [{determinism is true} {Dr. Freudlov correctly predicts what I will do}] [{she tells](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-115.jpg)
1. [{determinism is true} {Dr. Freudlov correctly predicts what I will do}] [{she tells me her prediction} {I’ll do something else}] 2. [{Dr. Freudlov tells me her prediction} {I’ll do something else}] [Dr. Freudlov doesn’t correctly predict what I’ll do] 3. [determinism is true] [{Dr. Freudlov doesn’t correctly predict what I’ll do} {she won’t tell me her prediction}] 115
![1 determinism is true Dr Freudlov correctly predicts what I will do she tells 1. [{determinism is true} {Dr. Freudlov correctly predicts what I will do}] [{she tells](https://slidetodoc.com/presentation_image_h2/20e420130c9a06fac92a198c65b1aeb0/image-116.jpg)
1. [{determinism is true} {Dr. Freudlov correctly predicts what I will do}] [{she tells me her prediction} {I’ll do something else}] 2. [{Dr. Freudlov tells me her prediction} {I’ll do something else}] [Dr. Freudlov correctly predicts what I’ll do] 3. [determinism is true] [ {Dr. Freudlov correctly predicts what I’ll do} {she will tell me her prediction}] 116
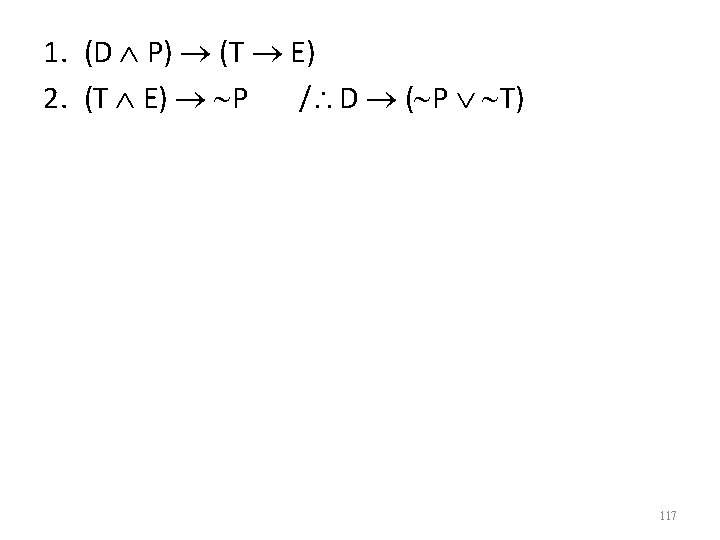
1. (D P) (T E) 2. (T E) P / D ( P T) 117

1. (D P) (T E) 2. (T E) P / D ( P T) 3. asm: (D ( P T)) 118

1. 2. 3. 4. 5. (D P) (T E) P / D ( P T) asm: (D ( P T)) D {from 3, NIF} ( P T) {from 3, NIF} 119

1. 2. 3. 4. 5. 6. 7. 8. 9. (D P) (T E) P / D ( P T) asm: (D ( P T)) D {from 3, NIF} ( P T) {from 3, NIF} P {from 5, NOR} T {from 5, NOR} (T E) {from 2 and 6, MP} E {from 7 and 8, CS} 120

1. (D P) (T E) 2. (T E) P / D ( P T) 3. asm: (D ( P T)) 4. D {from 3, NIF} 5. ( P T) {from 3, NIF} 6. P {from 5, NOR} 7. T {from 5, NOR} 8. (T E) {from 2 and 6, MP} 9. E {from 7 and 8, CS} 10. asm: (D P) {break 1} 121

1. (D P) (T E) 2. (T E) P / D ( P T) 3. asm: (D ( P T)) 4. D {from 3, NIF} 5. ( P T) {from 3, NIF} 6. P {from 5, NOR} 7. T {from 5, NOR} 8. (T E) {from 2 and 6, MP} 9. E {from 7 and 8, CS} 10. asm: (D P) {break 1} 11. P {from 4 and 10, CS} 12. D P {from 10; 6 contradicts 11, RAA} 122

1. (D P) (T E) 2. (T E) P / D ( P T) 3. asm: (D ( P T)) 4. D {from 3, NIF} 5. ( P T) {from 3, NIF} 6. P {from 5, NOR} 7. T {from 5, NOR} 8. (T E) {from 2 and 6, MP} 9. E {from 7 and 8, CS} 10. asm: (D P) {break 1} 11. P {from 4 and 10, CS} 12. D P {from 10; 6 contradicts 11, RAA} 13. T E {from 1 and 12, MP} 14. E {from 7 and 13, MP} 15. D ( P T) {from 3; 9 contradicts 14, RAA} 123

Refutation • A Refutation: – A set of truth conditions making all premises true and conclusion false. – Showing that the argument is invalid. • When assuming the negation of conclusion, it won’t lead to a contradiction. • By the truth-assignment of every simple wff, we can construct a refutation box. 124

Construct a Refutation Box • First Step and Second Step are the same as constructing a proof. • However, we can’t apply RAA, for we can’t derive a contradiction by applying S-rules and Irules to wffs. • So we assign each simple wff 1 or 0 in a way that makes all premises true but conclusion false. 125

For example 1. T 2. T (B M) 3. M H / B 126

1. 2. 3. 4. 5. 6. 7. T T (B M) M H / B asm: B B M {from 1 and 2, MP} M {from 4 and 5, DS} H {from 3 and 6, MP} No contradiction! 127

1. 2. 3. 4. 5. 6. 7. T T (B M) M H / B asm: B B M {from 1 and 2, MP} M {from 4 and 5, DS} H {from 3 and 6, MP} To make premises true and conclusion false: T = 1, B = 0 128

1. 2. 3. 4. 5. 6. 7. T T (B M) M H / B asm: B B M {from 1 and 2, MP} M {from 4 and 5, DS} H {from 3 and 6, MP} To make premises true and conclusion false: T = 1, B = 0 Since T (B M) = 1 and, given that T = 1 and B = 0, M = 1. 129

1. 2. 3. 4. 5. 6. 7. T T (B M) M H / B asm: B B M {from 1 and 2, MP} M {from 4 and 5, DS} H {from 3 and 6, MP} To make premises true and conclusion false: T = 1, B = 0 Since T (B M) = 1 and, given that T = 1 and B = 0, M = 1. To make M H = 1, given M = 1, H = 1. 130

1. T 2. T (B M) 3. M H / B Under the truth-assignment of T = 1, B = 0, M = 1, and H = 1, this argument is invalid. 131
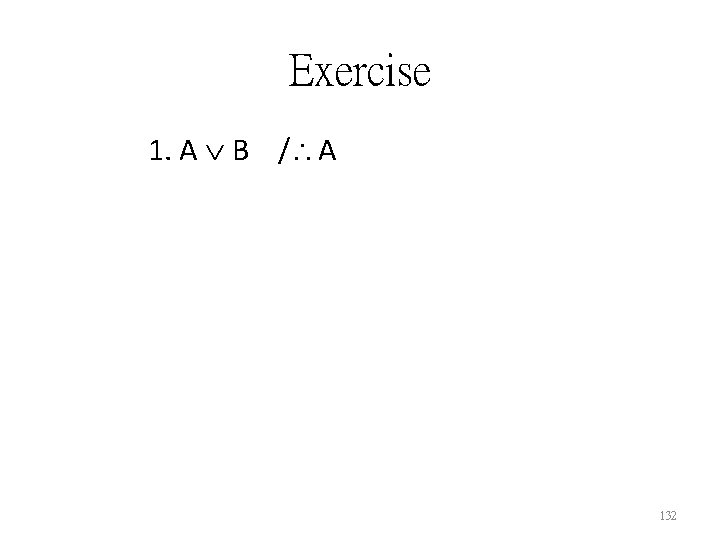
Exercise 1. A B / A 132

Exercise 1. A B / A 2. asm: A 133

Exercise 1. A B / A 2. asm: A 3. B {from 1 and 2, DS} 134

Exercise 1. A B / A 2. asm: A 3. B {from 1 and 2, DS} Assign A = 0 and A B = 1 135

Exercise 1. A B / A 2. asm: A 3. B {from 1 and 2, DS} Assign A = 0 and A B = 1 So B = 1 136

Exercise 1. A B / A 2. asm: A 3. B {from 1 and 2, DS} Under the truth-assignment of A = 0 B = 1, this argument is invalid. 137

5. Appendix: Model Theory • Two approaches to Validity: – Proof Theory: an argument is valid if and only if there is a formal proof of it. (an argument is a series of small steps, each based on S-rules and Irules) – Model Theory: an argument is valid if and only if there is a truth-table showing that no possible case has premises all true and conclusion false. 138

Model Theory • A model is an interpretation of formal language, such as propositional language. • As introduced at the beginning, PL contains two components: – Vocabulary – Formation Rules • Therefore, a model must interpret the vocabulary of PL. 139

Interpretation • Vocabulary contains two parts: – Logical constants (logical connectives) – Logical variables (propositional letters) • A model interprets logical connectives by truth functions and propositional letters by truth values (1 or 0). • Recall the truth-assignment test: – An argument is valid if and only if no possible truth-assignment can make all premises true and conclusion false. 140

Formal Explanation • A model for PL is an interpretation function I: – I( ): f (x) = 1 v(x) – I( ): f (<x, y>) = v(x) v(y) – I( ): f (<x, y>) = v(x) + v(y) v(x) v(y) – I( ): f (<x, y>) = v(y) v(x) v(y) – I(PL) = v(PL) (v: PL {0, 1}) 141