Firstorder Logic Limitation of propositional logic A very








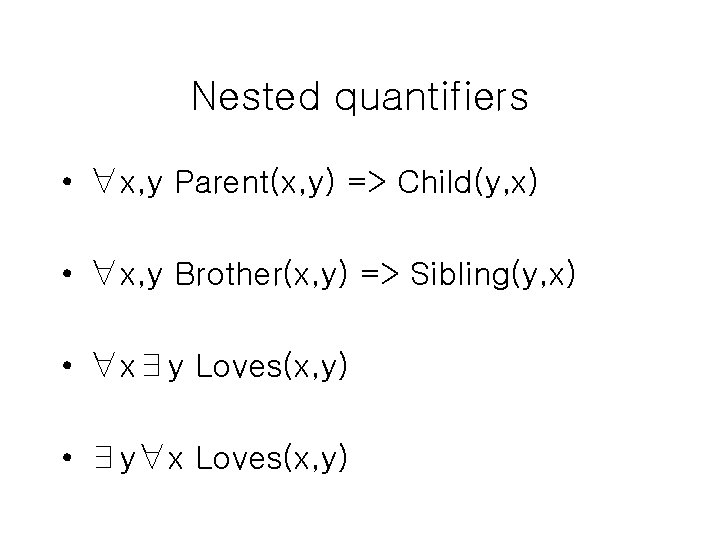


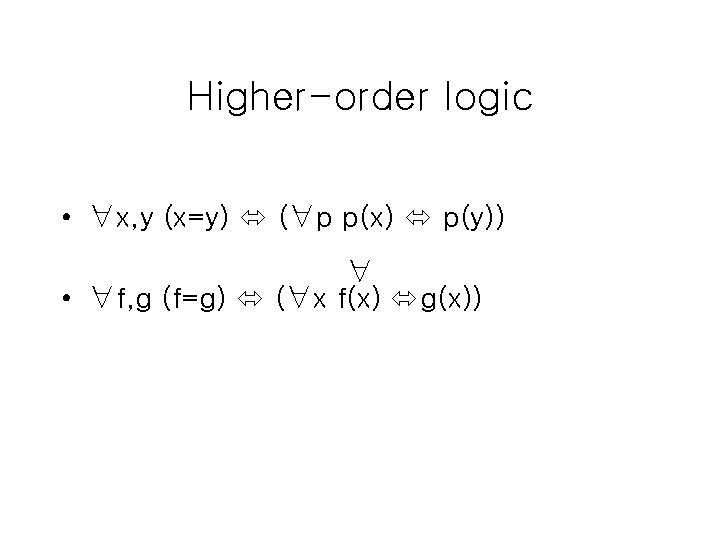






















- Slides: 37

논리와 응용 First-order Logic

Limitation of propositional logic • A very limited ontology • to need to the representation power • first-order logic

First-order logic • A stronger set of ontological commitments • A world in FOL consists of objects, properties, relations, functions • Objects people, houses, number, colors, Bill Clinton • Relations brother of, bigger than, owns, love • Properties red, round, bogus, prime • Functions father of, best friend, third inning of

Examples • “One plus two equals three” – objects : : one, two, three, one plus two – Relation : : equal – Function : : plus • “Squares neighboring the wumpus are smelly – Objects : : wumpus, square – Property : : smelly – Relation : : neighboring


Syntax and Semantics Sentence Atomic. Sentence | Sentence Connective Sentence | Auantifier Variable, …Sentence | (Sentence) Atomic. Sentence Predicate(Term, …) | Term=Term Function (Term, …) | Constant | Variable Connective | | | Quantifier | Constant A | X 1 | John | … Variable a | x | s | … Predicate Before | Han. Color | Raining | … Function Mother | Left. Leg. Of | … Figure 7. 1 The syntax of first-order logic (with equality) in BNF (Backus-Naur Form).

예 • • • Constant symbols : : A, B, John, Predicate symbols : : Round, Brother Function symbols : : Cosine, Father. Of Terms : : King John, Richard’s left leg Atomic sentences : : Brother(Richard, John), Married(Father. Of(Richard), Mother. Of(John)) • Complex sentences : : Older(John, 30)=>~younger(John, 30)

Quantifiers • World = {a, b, c} • Universal quantifier (∀) ∀x Cat(x) => Mammal(x) Cat(a) => Mammal(a) & Cat(a) => Mammal(a) • Existential quantifier (∃) ∃x Sister(x, Sopt) & Cat(x)
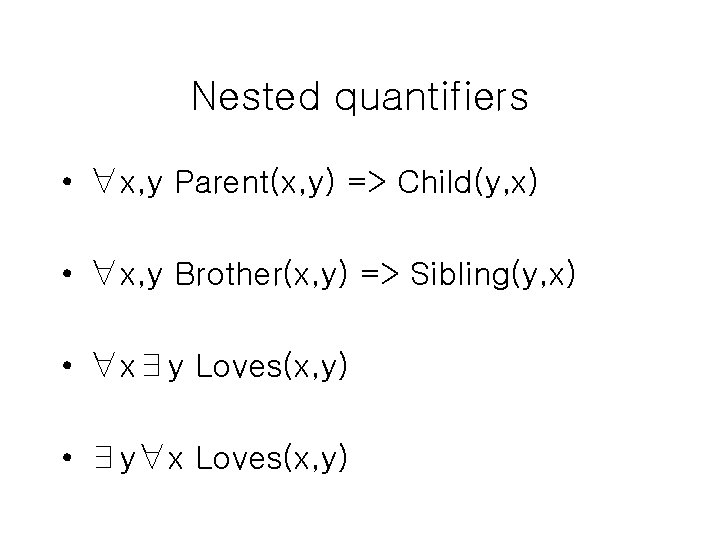
Nested quantifiers • ∀x, y Parent(x, y) => Child(y, x) • ∀x, y Brother(x, y) => Sibling(y, x) • ∀x∃y Loves(x, y) • ∃y∀x Loves(x, y)

De Morgan’s Rule ∀x ~P ~∃x P ~P&~Q ~(P v Q) ~∀x P ∃x ~P ~(P&Q) ~P v ~Q ∀x P ~∃x ~P P&Q ~(~P v ~ Q) ∃x P ~∀x ~P P v Q ~(~P&~Q)

Equality • Identity relation • Father(John) = Henry • ∃x, y Sister(Spot, x) & Sister(Spot, y) & ~(x=y) ≠ ∃x, y Sister(Spot, x) & Sister(Spot, y)
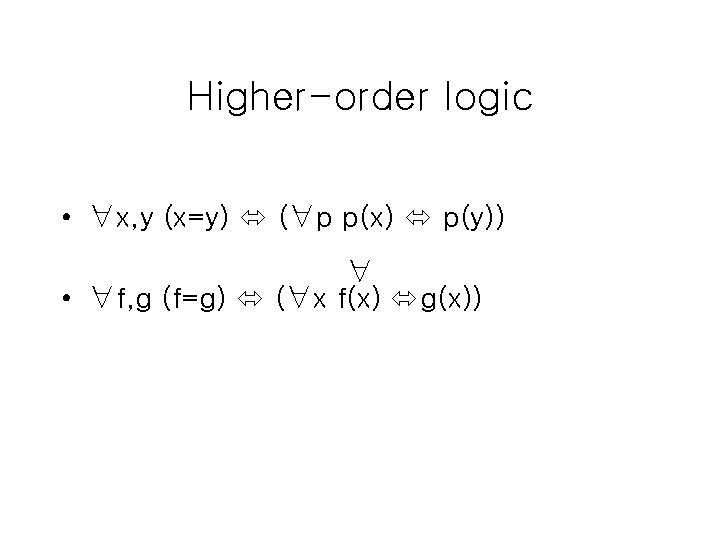
Higher-order logic • ∀x, y (x=y) (∀p p(x) p(y)) ∀ • ∀f, g (f=g) (∀x f(x) g(x))

-expression • x, y x 2 – y 2 • -expression can be applied to arguments to yield a logical term in the same way that a function can be • ( x, y x 2 – y 2)(25, 24) = 252 -242 = 49 • x, y Gender(x) ≠Gender(y) & Address(x) = Address(y)

∃! (The uniqueness quantifier) • ∃!x King(x) • ∃x King(x) & ∀y King(y) => x=y world를 고려하여 보여주면 => object가 1, 2, 3개일 때 {a} w 0 king={}, w 1 king={a} w 1만 model {a, b} w 0 king={}, w 1 king={a}, w 2 {b}, w 3 {a, b} w 1, w 2만 model

Representation of sentences by FOPL • One’s mother is one’s female parent ∀m, c Mother(c)=m Female(m) & Parent(m) • One’s husband is one’s male spouse ∀w, h Husband(h, w) Male(h) & Spouse(h, w) • Male and female are disjoint categories ∀x Male(x) ~Female(x) • A grandparent is a parent of one’s parent ∀g, c Grandparent(g, c) ∃p parent(g, p) & parent(p, g)

Knowledge Base • A set of representations of facts about the world • Knowledge representation language – tell : what has been told to the knowledge base previously – ask : a question and the answer • Inference : what follows from what the KB has been Telled • Background knowledge : a knowledge base which may initially contained • Sentence : individual representation of a fact

Knowledge base • The knowledge level : : saying what it knows to KB “Golden Gates Bridge links San Francisco and Marin Country • The logical level : : the knowledge is encoding into sentences Links(GGBridge, SF, Marin) • The implementation level : : the level that runs on the agent architecture (data structures to represent knowledge or facts)

Knowledge • declarative/procedural – love(john, mary). – can_fly(X) : - bird(X), not(can_fly(X)), !. • learning : general knowledge about the environment given a series of percepts • Commonsense knowledge

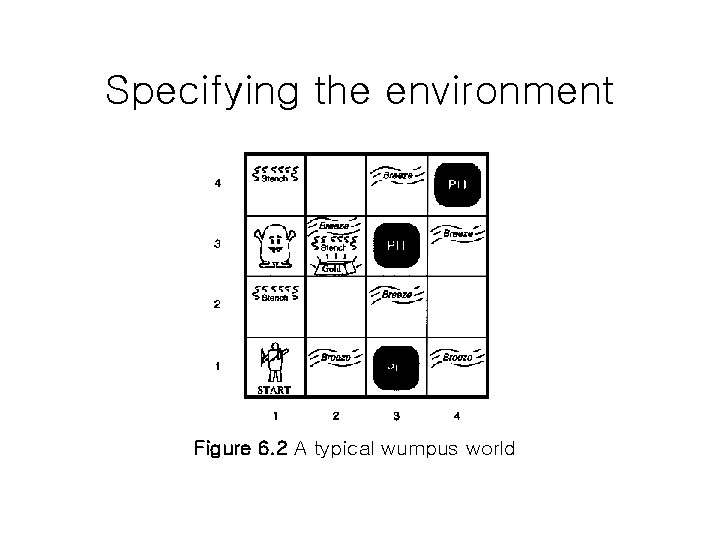
Specifying the environment Figure 6. 2 A typical wumpus world

Domain specific knowledge • Domain specific knowledge – In the squares directly adjacent to a pit, the agent will perceive a breeze • Commonsense knowledge – logical reasoning – stench(1, 2) & ~setnch(2, 1) ~wumpus(2, 2) – wumpus(1, 3) stench(2, 1) & stench(2, 3) & stench(1, 4)

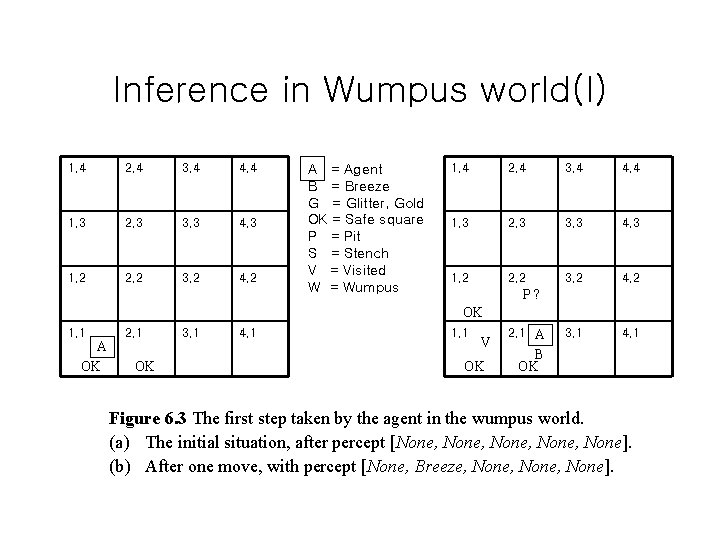
Inference in Wumpus world(I) 1, 4 2, 4 3, 4 4, 4 1, 3 2, 3 3, 3 4, 3 1, 2 2, 2 3, 2 4, 2 A = Agent B = Breeze G = Glitter, Gold OK = Safe square P = Pit S = Stench V = Visited W = Wumpus 1, 4 2, 4 3, 4 4, 4 1, 3 2, 3 3, 3 4, 3 1, 2 2, 2 3, 2 4, 2 3, 1 4, 1 P? OK 1, 1 A OK 2, 1 OK 3, 1 4, 1 1, 1 V OK 2, 1 A B OK Figure 6. 3 The first step taken by the agent in the wumpus world. (a) The initial situation, after percept [None, None]. (b) After one move, with percept [None, Breeze, None, None].

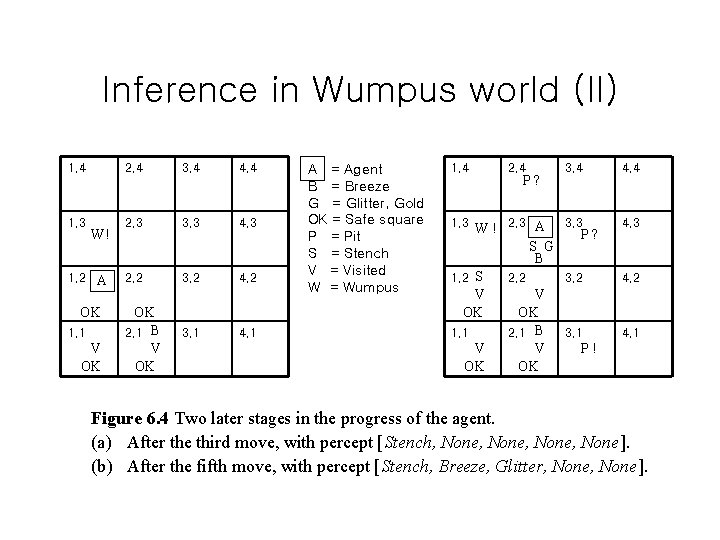
Inference in Wumpus world (II) 1, 4 1, 3 W! 1, 2 A OK 1, 1 V OK 2, 4 3, 4 4, 4 2, 3 3, 3 4, 3 2, 2 3, 2 4, 2 3, 1 4, 1 OK 2, 1 B V OK A = Agent B = Breeze G = Glitter, Gold OK = Safe square P = Pit S = Stench V = Visited W = Wumpus 1, 4 1, 3 2, 4 P? 3, 4 W ! 2, 3 A 3, 3 P ? S G B 1, 2 S 2, 2 3, 2 V V OK OK 1, 1 2, 1 B 3, 1 V V P! OK OK 4, 4 4, 3 4, 2 4, 1 Figure 6. 4 Two later stages in the progress of the agent. (a) After the third move, with percept [Stench, None, None]. (b) After the fifth move, with percept [Stench, Breeze, Glitter, None].

Representation, Reasoning, and Logic • Syntax : the possible configurations that constitute sentences • Semantics : the facts in the world to which the sentences refer

The logical reasoning Figure 6. 5 The connection between sentences and facts is provided by the semantics of the language. The property of one fact following from some other facts is mirrored by the property of one sentence being entailed by some other sentences. Logical inference generates new sentences that are entailed by existing sentences.

Wrong logical reasoning FIRST VILLAGER: We have found a witch. May we burn her? ALL: A witch! Burn her! BEDEVERE: Why do you think she is a witch? SECOND VILLAGER: She turned me into a newt. BEDEVERE: A newt? SECOND VILLAGER (after looking at himself for some time): I got better. ALL: Burn her anyway. BEDEVERE: Quiet! There are ways of telling whether she is a witch. BEDEVERE: Tell me … What do you do with witches? ALL: Burn them. BEDEVERE: And what do you burn, apart from witches? FOURTH VILLAGER: … Wood? BEDEVERE: So why do witches burn? SECOND VILLAGER: (pianissimo) Because they’re made of wood? BEDEVERE: Good. ALL: I see. Yes, of course. BEDEVERE: So how can we tell if she is made of wood? FIRST VILLAGER: Make a bridge out of her. BEDEVERE: Ah … but can you not also make bridges out of stone? ALL: Yes, of course … um … er … BEDEVERE: Does wood sink in water? ALL: No, no, it floats. Throw her in the pond. BEDEVERE: Wait … tell me, what also floats on water? ALL: Bread? No, no no. Apples … gravy … very small rocks … BEDEVERE: No, no no. KING ARTHUR: A duck! (They all turn and look at ARTHUR. BEDEVERE looks up very impressed. ) BEDEVERE: Exactly. So … logically … FIRST VILLAGER (beginning to pick up the thread): If she. . Weight the same as a duck … she’s made of wood. BEDEVERE: And therefore? ALL: A witch!

Ontological and epistemological commitments • Ontological commitments : : to do with the nature of reality – Propositional logic(true/false), Predicate logic, Temporal logic • Epistemological commitments : : to do with the possible states of knowledge an agent can have using various types of logic – degree of belief – fuzzy logic

Commitments Formal languages and their and ontological and epistemological commitments Language Ontological Commitment (What exists in the world) Epistemological Commitment (What an agent believes about facts) Propositional logic First-order logic Temporal logic Probability theory Fuzzy logic facts, objects, relations times facts degree of truth true/false/unknown degree of belief 0… 1

Inference Rules for propositional logic § Modus Ponens or Implication-Elimination: (From an implication => , and the premise of the implication, you can infer the conclusion. ) § And-Elimination: (From a conjunction, you can infer any of the conjuncts. ) § And-Introduction: (From a list of sentences, you can infer their 1 2 … n Double-Negation Elimination: (From a doubly negated Unit Resolution: (From a disjunction, if one of the disjuncts is false, then you can infer the other one is true. ) § sentence, you can infer a positive sentence. ) § i Or-Introduction: (From a sentence, you can infer its disjunction with anything else at all. ) § i 1, 2, …, n 1 2 … n conjunction. ) § 1 2 … n , Resolution: (This is the most difficult. Because cannot be both true and false, one of the other disjucts must be true in one of the premises. Or equivalently, implication is transitive. ) , or equivalently => , => Figure 6. 13 Seven inference for propositional logic. The unit resolution rule is a special case of the resolution rule, which in turn is a special case of the full resolution rule for first-order logic discussed in Chapter 9.

Complexity of propositional inference • NP-complete • Monotonicity – If KB 1╞ then (KB 1 ∪ KB 2) ╞ • Horn clause logic – polynomial time complexity – P 1∧P 2∧…. ∧Pn ⇒ Q

Wumpus world • Initial state ~S 1, 1 ~S 2, 1 S 1, 2 ~B 1, 1 B 2, 1 ~B 1, 2 • Rule R 1: R 2: R 3: R 4: ~S 1, 1 ~S 2, 1 ~S 1, 2 -> ~W 1, 1 & ~W 1, 2 & ~W 2, 1 -> ~W 1, 1 & ~W 2, 2 & ~W 3, 1 -> ~W 1, 1 & ~W 1, 2 & ~W 2, 2 & ~W 1, 3 -> W 1, 3 V W 1, 2 V W 2, 2 V W 1, 2

Finding the wumpus • Inference process – Modus ponens : ~S 1, 1 and R 1 ~W 1, 1 & ~W 1, 2 & ~W 2, 1 – And-Elimination ~W 1, 1 ~W 1, 2 ~W 2, 1 – Modus ponens and And-Elimination: ~W 2, 2 ~W 2, 1 ~W 3, 1 – Modus ponens S 1, 2 and R 4 W 1, 3 V W 1, 2 V W 2, 2 V W 1, 1

Inference process(cont. ) – unit resolution ~W 1, 1 and W 1, 3 V W 1, 2 V W 2, 2 V W 1, 1 W 1, 3 V W 1, 2 V W 2, 2 – unit resolution ~W 2, 2 and W 1, 3 V W 1, 2 V W 2, 2 W 1, 3 V W 1, 2 – unit resolution ~W 1, 2 and W 1, 3 V W 1, 2 W 1, 3

Representation of sentences by FOPL • A sibling is another child of one’s parents ∀x, y Sibling(x, y) x≠y & ∃p Parent(p, x) & Parent(p, y) • Symmetric relations ∀x, y Sibling(x, y) Sibling(y, x)

The domain of sets (I) • The only sets are the empty set and those made by adjoining something to a set : ∀s Set(s) (s=Empty. Set) v (∃x, s 2 Set(s 2) & s=Adjoin(x, s 2)) • The empty set has no elements adjoined into it. ~∃x, s Adjoin(x, s)=Empty. Set • Adjoining an element already in the set has no effect ∀x, s Member(x, s) s=Adjoin(x, s) • The only members of a set are the elements that were adjoined into it ∀x, s Member(x, s) ∃y, s 2 (s=Adjoin(y, s 2) & (x=y v Member(x, s)))

The domain of sets (II) • A set is a subset of another if and only if all of the first set’s are members of the second set : ∀s 1, s 2 Subset(s 1, s 2) (∀x Member(x, s 1) => member(x, s 2)) • Two sets are equal if and only if each is a subset of the other: ∀s 1, s 2 (s 1=s 2) (Subset(s 1, s 2) & Subset(s 2, s 1))

The domain of sets (III) • An object is a member of the intersection of two sets if and only if it is a member of each of sets : ∀x, s 1, s 2 Member(x, Intersection(s 1, s 2)) Member(x, s 1) & Member(x, s 2) • An object is a member of the union of two sets if and only if it is a member of either set : ∀x, s 1, s 2 Member(x, Union(s 1, s 2)) Member(x, s 1) v Member(x, s 2)

Asking questions and getting answers • Tell(KB, (∀m, c Mother(c)=m Female(m) & Parent(m, c))) • …… • Tell(KB, (Female(Maxi) & Parent(Maxi, Spot) & Parent(Spot, Boots))) • • Ask(KB, Grandparent(Maxi, Boots) Ask(KB, ∃x Child(x, Spot)) Ask(KB, ∃x Mother(x)=Maxi) Substitution, unification, {x/Boots}