Fakultet kemijskog inenjerstva i tehnologije Matematike metode u

Fakultet kemijskog inženjerstva i tehnologije Matematičke metode u kemijskom inženjerstvu FOURIEROVI REDOVI I INTEGRALI Ana Škrobica Andreja Prtenjak Studenti : 2006/2007

UVOD • pri rješavanju različitih inženjerskih problema koriste se periodične funkcije: Ø trigonometrijske funkcije, sinus i kosinus • imaju važnost u praktičnoj primjeni Ø u proučavanju signala, titranja, rezonancije i pri rješavanju problema vezanih uz obične i parcijalne diferencijalne jednadžbe

PERIODIČNE FUNKCIJE • temeljna skupina funkcija koje se upotrebljavaju u harmonijskoj analizi • harmonička analiza predstavlja razvoj dotičnih periodičnih funkcija u odgovarajući Fourierov red • funkcija f : R → R je periodična funkcija ako postoji T ≠ 0 takav da vrijedi: f(x + T) = f(x) za svaki x koji je element skupa R realnih brojeva - broj T se zove period funkcije f(x)

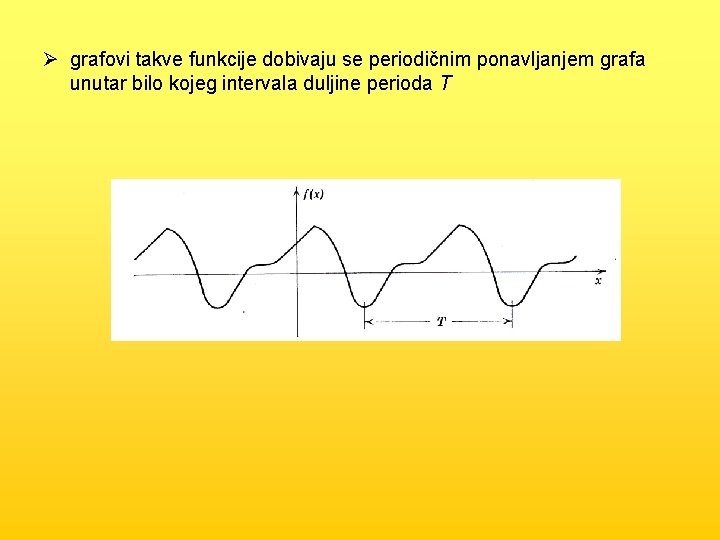
Ø grafovi takve funkcije dobivaju se periodičnim ponavljanjem grafa unutar bilo kojeg intervala duljine perioda T

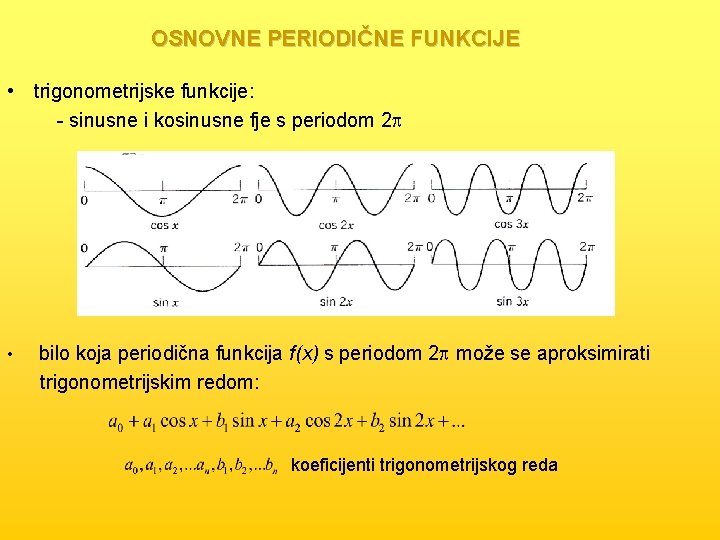
OSNOVNE PERIODIČNE FUNKCIJE • trigonometrijske funkcije: - sinusne i kosinusne fje s periodom 2 p • bilo koja periodična funkcija f(x) s periodom 2 p može se aproksimirati trigonometrijskim redom: koeficijenti trigonometrijskog reda

RAZVOJ PERIODIČNIH FUNKCIJA PERIODA 2 p U FOURIEROVE REDOVE • da bi razvili odgovarajuću periodičnu funkciju s periodom 2 p u Fourierov red potrebno je izračunati koeficijente Fourierovog reda koje računamo na temelju ovih izraza:

Izvod koeficijenata • pretpostavimo da je f(x) periodična funkcija s periodom 2 p, koju možemo prikazati trigonometrijskim redom (1) • želimo odrediti koeficijente an i bn • a 0 dobijemo integrirajući izraz s obje strane od –p do p: • prvi dio izraza na desnoj strani jednak je 2 pa 0 dok su ostali integralni izrazi jednaki nuli, te provedbom integracije dobivamo:

Ø sada ćemo redom izračunati koeficijente sličnim postupkom • množit ćemo izraz (1) s cos mx, (m je bilo koji fiksni pozitivan broj), slijedi: • integrirajući član po član proizlazi da je desna strana jednaka: • prvi integral i zadnji integral jednaki su nuli (jer je podintegralni izraz neparna funkcija) • primjenjujući svojstva parnosti i neparnosti funkcije na drugi integral dobivamo izraz:

• prvi integral s desne strane jednak je nuli za svaki m i n koji se uzimaju u obzir, i posljednji integral je jednak nuli kada je ili iznosi p za svaki • proizlazi da je desna strana jednaka am p i dobiva se :

Ø možemo izračunati koeficijente b 1, b 2, . . . pri čemu množimo izraz (1) sa sin mx, (m je bilo koji fiksni pozitivan broj) • integracijom tog izraza od –p dobivamo: • integrirajući član po član, desna strana izraza je jednaka: • prvi integral jednak je nuli, sljedeći integral također je jednak nuli za svaki n = 1, 2, . . . • posljednji i prvi član jednak je nuli, desna strana postaje bm p, dakle:

EULEROVE FORMULE • Upisujući n umjesto m u prethodno dobivene formule za koeficijente, dobivaju se Eulerove formule: formule

FOURIEROV RED • pomoću periodične funkcije f(x) s danim periodom 2 p, možemo izračunati koeficijente an i bn , prema Eulerovim formulama i formirati trigonometrijski niz: Ø ovaj red se naziva Fourierov red i odgovara f(x) Ø koeficijente nazivamo Fourierovi koeficijenti funkcije f(x)

TEOREM 1. • Ako imamo periodičku funkciju f(x) sa periodom 2 p koja je djelomično neprekidna unutar intervala i ukoliko postoji njena derivacija i s lijeve i sa desne strane u svakoj točki unutar intervala integracije tada za odgovarajući Fourierov red kažemo da je konvergentan.

PRIMJEDBA: • ukoliko Fourierov red odgovarajuće funkcije f(x) konvergira, kao što je objašnjeno u teoremu 1, red se naziva Fourierovim redom funkcije f(x) pa možemo pisati: - f(x) predstavlja Fourierov red dotične funkcije • ovaj niz je konvergentan, i novodobiveni red imat će sumu jednaku sumi originalnog reda pa se može pisati:

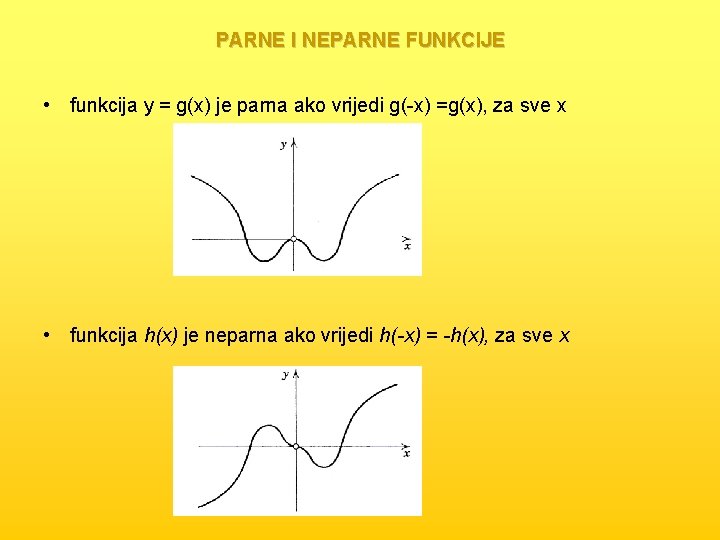
PARNE I NEPARNE FUNKCIJE • funkcija y = g(x) je parna ako vrijedi g(-x) =g(x), za sve x • funkcija h(x) je neparna ako vrijedi h(-x) = -h(x), za sve x

TEOREM 1. • Fourierov red bilo koje parne periodične funkcije s periodom 2 p je kosinusni Fourierov red koji zapisujemo: s koeficijentima • Fourierov red bilo koje neparne periodične funkcije perioda 2 p je tzv. sinusni Fourierov red koji zapisujemo: s koeficijentima

TEOREM 2. • Fourierovi koeficijenti sume f 1 + f 2 su suma odgovarajućih Fourierovih koeficijenata od f 1 i f 2.

FUNKCIJE KOJE IMAJU PROIZVOLJAN PERIOD • prijelaz iz funkcije perioda 2 p na funkcije koje imaju period T je jednostavan zbog toga što se može provesti izmjena skale • ako je f(t) funkcija perioda T, tada možemo uvesti novu varijablu x tako da nova funkcija, kao funkcija od x, ima period 2 p • ako je onda vrijedi • Fourierov red je sljedećeg oblika čije koeficijente računamo prema sljedećim formulama:

• možemo primjeniti i ove formule direktno ali promjenom perioda T pojednostavljujemo jednadžbu: • interval integracije se mijenja i postaje: • posljedično, dobivamo Eulerove formule za Fourierove koeficijente funkcije f(t): • Fourierov red u kojem je varijabla x zamjenjena varijablom t ima oblik:

TEOREM 1. • Fourierov red parne funkcije f(t) perioda T je kosinusni Fourierov red s koeficijentima: • Fourierov red neparne funkcije f(t) perioda T je sinusni Fourierov red s koeficijentima:

POLUPERIODIČNO PROŠIRENJE REDA • neka funkcija f(t) ima period T=2 l, ako je ta funkcija parna dobiva se Fourierov kosinusni red : s koeficijentima • ako je ta funkcija f(x) neparna funkcija dobiva se Fourierov sinusni red: s koeficijentima

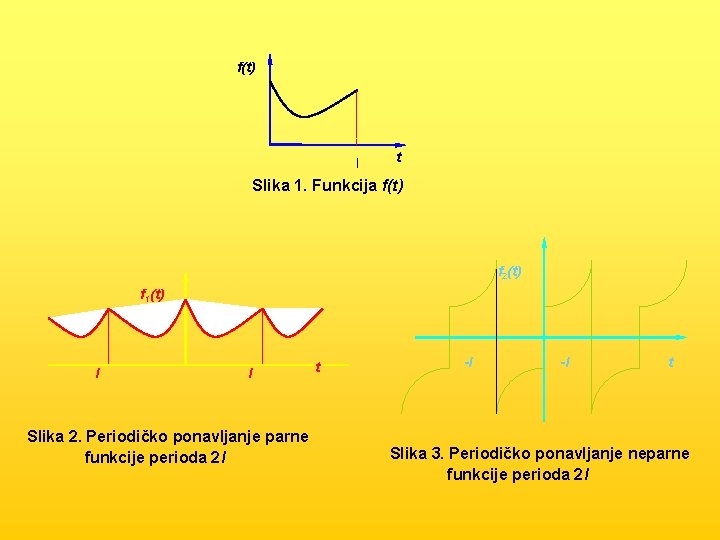
f(t) l t Slika 1. Funkcija f(t) f 2(t) f 1(t) l l Slika 2. Periodičko ponavljanje parne funkcije perioda 2 l t -l -l t Slika 3. Periodičko ponavljanje neparne funkcije perioda 2 l

FOURIEROV INTEGRAL • kako mnogi praktični problemi ne uključuju periodične funkcije poželjno je generalizirati metodu Fourierovog reda i na neperiodične funkcije • imamo periodičnu funkciju f. T(x) sa periodom T i možemo ju pisati pomoću Fourierovog reda : • ako uzmemo da vrijedi : • uvrstimo an i bn prema Eulerovim formulama, označimo varijablu integracije sa n dobiva se : • ako je :

• onda 2/T = ∆w / p i možemo pisati Fourierov red u obliku (1) - vrijedi za bilo koji fiksni T, proizvoljno velik ali konačan • neka T → ∞ i pretpostavimo da rezultirajuća neperiodična funkcija postoji • 1/T → 0 i vrijednost prvog člana da desnoj strani izraza (1) se približava nuli • ∆w = 2 p/T → 0 , beskonačan red (1) postaje integral od 0 do ∞ koji predstavlja f(x)

• ako uvedemo supstituciju • izraz se može pisati u obliku Ø ovakav oblik f(x) se naziva Fourierov integral

TEOREM 1. • Ako je f(x) po djelovima neprekinuta na svakom konačnom intervalu i može se s lijeve i desne strane derivirati u svakoj točki i ako integral postoji onda se f(x) može pisati pomoću Fourierovog integrala. U točki gdje je f(x) prekinuta vrijednost Fourierova integrala je jednaka granicama lijeve i desne strane funkcije f(x) u toj točki prekida.

• ako je f(x) parna funkcija, onda je B(w) = 0 i slijedi • Fourierov integral se može pisati u jednostavnijem obliku • ako je f(x) neparna funkcija, onda je A(w) = 0 i slijedi • Fourierov integral se može pisati prema

ORTOGONALNE FUNKCIJE • gm(x) i gn(x) realne funkcije, definirane u intervalu • postoji integral produkta na tom intervalu kojeg ćemo označiti kao: • za funkcije kažemo da su ortogonalne u intervalu ako je integral jednak nuli: • ne-negativan korijen od se zove norma od i označava se sa

Osnovna pretpostavka Ø Sve funkcije koje se pojavljuju su ograničene i imaju svojstvo da integrali koji se pojavljuju postoje i da njihove norme nisu nula. • Ortogonalni skup u intervalu čije funkcije imaju normu 1 zadovoljavaju relaciju: - takav skup se naziva ortonormiran skup funkcija u intervalu • skup • mogućnost prikaza zadane funkcije f(x) pomoću bilo kojeg ortogonalnog skupa g 1(x), g 2(x). . . oblika: je ortogonalan na intervalu duljine 2 p

• ako red konvergira i predočuje f(x) nazivamo ga generaliziran Fourierov red funkcije f(x) • njegove koeficijente nazivamo Fourierovim konstantama funkcije f(x) s obzirom na taj ortogonalni skup funkcija • konstante određujemo pomoću izraza: • integral za koji je jednak je kvadratu iznosa , dok su ostali integrali jednaki nuli jer su funkcije međusobno ortogonalne

• ako je skup funkcija ortonormiran tada Fourierove konstante zadovoljevaju Besselovu nejednakost: • red na lijevoj strani konvergira pa slijedi: pri

LITERATURA • A. E. Kreyzig , “Advanced engineering mathematics”, John Wiley & Sons Inc (1995) • I. Ivanšić, “Fourierovi redovi. Diferencijalne jednadžbe”, Odjel za matematiku, Sveučilište J. J. Strossmayera u Osijeku (2000. )