EQUAZIONI DI 2 GRADO Classe II a s

EQUAZIONI DI 2° GRADO Classe II a. s. 2010/2011 Prof. ssa Rita Schettino

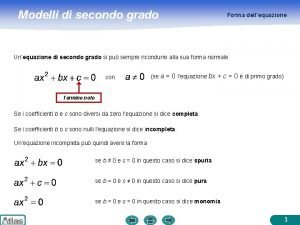
DEFINIZIONE Un’equazione, in , si dice di secondo grado se, ridotta a forma normale, è del tipo: Ø Ø con a 0 Risolvere un’equazione significa determinare i due valori reali 2 di x (soluzioni o radici), se esistono, che soddisfano l’equazione data prof. ssa R. Schettino Ø

DEFINIZIONE Si definisce DISCRIMINANTE dell’equazione e si indica con la lettera greca (delta) il termine E’ importante il segno di perché da esso scaturisce la realtà delle soluzioni dell’equazione prof. ssa R. Schettino 3

FORMULE RISOLUTIVE prof. ssa R. Schettino 4

OSSERVAZIONI • • prof. ssa R. Schettino • Si noti che le formule per la pura e la spuria si ottengono dalla prima sostituendo rispettivamente b=0 e c=0 (lo si faccia per esercizio) Si noti che i radicali presenti nelle formule sono di indice pari (radicali quadratici) e quindi vanno fatte le considerazioni per i radicali algebrici Come si sa l’esistenza dei suddetti radicali dipende dal segno del radicando , quindi Ø Se 0 il radicale esiste in ed ammette due valori quindi l’equazione ammette due soluzioni reali Ø Se < 0 il radicale non esiste in quindi l’equazione risulta impossibile in 5

OSSERVAZIONI In più Se > 0 i valori dei due radicali sono opposti quindi le soluzioni sono reali e distinte Ø Se = 0 il valore dei due radicali è 0 quindi le soluzioni sono reali e coincidenti Ø Pertanto 6 prof. ssa R. Schettino

ESEMPI prof. ssa R. Schettino 7

ESEMPI prof. ssa R. Schettino 8

prof. ssa R. Schettino • Dagli esempi si evince che: Ø Individuato il tipo di equazione, si applica la relativa formula facendo massima attenzione ai segni dei coefficienti a, b e c ØCalcolato il , se > 0 si determinano le soluzioni reali e distinte; se = 0 soluzioni reali e coincidenti oppure se <0 l’equazione si classifica “impossibile in ” 9

QUADRO RIASSUNTIVO >0 soluzioni reali e distinte x 1 x 2 =0 soluzioni reali e coincidenti x 1=x 2 <0 equazione impossibile in prof. ssa R. Schettino (imparare BENISSIMO tali condizioni) 10

SOMMA E PRODOTTO DELLE SOLUZIONI Dalla formula risolutiva si ricava che: si può osservare che risulta prof. ssa R. Schettino Ciò significa che è possibile determinare la somma s e il prodotto p delle soluzioni di un’equazione di 2° grado utilizzando i coefficienti, senza dover risolvere l’equazione Ed inoltre potendo scrivere un’equazione nella forma 11

SOMMA E PRODOTTO DELLE SOLUZIONI Di qui scaturiscono i seguenti tipi di esercizi: Ø Determinare prof. ssa R. Schettino immediatamente le soluzioni di semplici equazioni cercando due numeri (qualora esistano perché > 0) che abbiano somma s e prodotto p (lo si può fare a mente) Ø Determinare due numeri reali di cui siano dati la loro somma e il loro prodotto Ø Impostare un’equazione che ammetta come soluzioni due numeri prefissati, sostituendo la loro somma s come coefficiente di x e il loro prodotto p come termine noto 12

ESEMPI prof. ssa R. Schettino 13

ESEMPI prof. ssa R. Schettino 14

ESEMPI prof. ssa R. Schettino 15

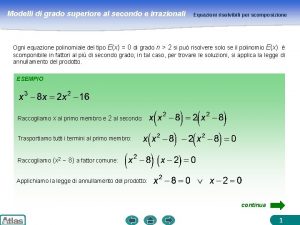
SCOMPOSIZIONE DI UN TRINOMIO DI 2° GRADO • • • prof. ssa R. Schettino • Può presentarsi il caso di dover scomporre in fattori un trinomio di 2° grado che non sia un quadrato perfetto La teoria delle equazioni di 2° grado ci permette di risolvere tale questione Si considera l’equazione associata al trinomio dato, si risolve con l’applicazione della formula risolutiva determinando le soluzioni x 1 e x 2 Infine il trinomio si scompone nel seguente modo: 16

ESEMPIO Scomporre in fattori il trinomio 2 x 2+3 x-2 Si considera 2 x 2+3 x-2=0 le cui soluzioni sono x 1= -2 e x 2 = ½ Quindi il trinomio si scompone in 2(x+2)(x-1/2) che, svolgendo i calcoli, diventa (x+2)(2 x-1) Cosa succede se l’equazione associata al trinomio non ammette soluzioni reali? Si spieghi perché i trinomi x 2 -x+1 o x 2+x-1 o i binomi x 2+1 o x 2 +3 (somme di due quadrati) non sono scomponibili prof. ssa R. Schettino 17

REGOLA DI CARTESIO Questa prof. ssa R. Schettino regola consente di conoscere il segno delle radici di un’equazione di 2° grado senza determinarle numericamente Considerati i coefficienti e termine noto di un’equazione in forma normale a, b e c si dice “ permanenza di segno” se due termini consecutivi (ossia a e b oppure b e c) hanno lo stesso segno; si dice “variazione di segno” se due termini consecutivi hanno segno opposto. 18

REGOLA DI CARTESIO Es: l’equazione 3 x 2 -5 x-1=0 ammette due soluzioni reali e distinte (perché a e c sono discordi quindi è sicuramente > 0) : una positiva ( che corrisponde alla variazione di segno di a=3 e b=-5) e una negativa (che corrisponde alla permanenza di segno di b=-5 e c=-1) prof. ssa R. Schettino La regola di Cartesio afferma che: In un’equazione in cui 0 (quindi ammette radici reali) Ad ogni permanenza corrisponde una soluzione negativa Ad ogni variazione corrisponde una soluzione positiva 19

Es: l’equazione 7 x 2+14 x+1=0 , per cui è 0 (verificare), ammette due soluzioni negative corrispondenti alle due permanenze di segno (a=7 e b = 14; b=14 e c=1) prof. ssa R. Schettino 20

DEFINIZIONE DI EQUAZIONE PARAMETRICA in cui si nota che il secondo coefficiente e il termine noto sono espressi in funzione del parametro k. Ciò significa che ad ogni valore reale del parametro corrisponde una precisa equazione di 2° grado che ammetterà soluzioni o sarà impossibile prof. ssa R. Schettino Equazione parametrica di 2° grado è un’equazione in cui i coefficienti a , b o il termine noto c dipendono da un parametro letterale variabile in , indicato ad esempio con la lettera k. Es: 21

Pertanto quando si studia o discute un’equazione parametrica, si sta studiando una famiglia di infinite equazioni, ognuna delle quali si ottiene assegnando un valore al parametro k. Si tratta generalmente di scoprire quale o quali valori del parametro danno luogo ad equazioni di quella famiglia che rispettano condizioni richieste. prof. ssa R. Schettino 22

Per capire: 3 x 2 -5 x+k 2 -4=0 è un’equazione parametrica perché il termine noto k 2 -4 assume valori diversi a seconda del valore assegnato a k Infatti se k = 1 l’equazione diventa: 3 x 2 -5 x-3=0 k = 3 l’equazione diventa 3 x 2 -5 x+5=0 Se k = -2 l’equazione diventa 3 x 2 -5 x=0 Se k = 0 l’equazione diventa 3 x 2 -5 x-4=0 e così via prof. ssa R. Schettino Se 23

Si prof. ssa R. Schettino noti che nel primo e quarto esempio si sono ottenute equazioni complete con soluzioni reali e distinte, nel secondo caso si è ottenuta un’equazione completa impossibile in , nel terzo caso un’equazione spuria che ammette una soluzione nulla Studiare l’equazione parametrica dell’esempio, significa determinare per quali valori di k si ottengono equazioni che rispondono a precise richieste Ad esempio, si potrebbe determinare quali valori del parametro danno equazioni con soluzioni coincidenti, oppure quali valori del parametro danno equazioni con soluzioni opposte o, ancora, quali valori del parametro danno equazioni che ammettono soluzioni reali, e così via. 24

FORMULE IMPORTANTI FORMULA DA IMPORRE Soluzioni reali e distinte = b 2 -4 ac > 0 Soluzioni reali e coincidenti =b 2 -4 ac = 0 Soluzioni complesse o equazione impossibile in =b 2 -4 ac < 0 Somma delle radici s = m Prodotto delle radici p = n Soluzioni opposte x 1=-x 2 prof. ssa R. Schettino CONDIZIONE RICHIESTA x 1 + x 2 = Soluzioni reciproche Somma dei quadrati delle radici x 12+x 22=q Somma dei cubi delle radici x 13+x 23=q 25

1° ESEMPIO DI STUDIO DI UN’EQUAZIONE PARAMETRICA DI 2° GRADO Determinare il valore del parametro m affinché l’equazione x 2 -(m-3)x+m 2+3 m+3=0 abbia: b) c) a) Una soluzione nulla (= 0) Una soluzione reciproca dell’altra La somma dei quadrati delle soluzioni sia uguale a 23 prof. ssa R. Schettino a) Studiamo caso per caso: Affinché una soluzione sia nulla bisogna che l’equazione sia spuria e quindi che il termine noto sia uguale a 0. Perciò imponendo che il termine noto dell’equazione data m 2+3 m+3 sia uguale a 0 determiniamo i valori di m perché l’equazione sia spuria e che abbia perciò una soluzione nulla, condizione richiesta dall’esercizio 26

a) Perciò dobbiamo risolvere l’equazione m 2+3 m+3 = 0 Applicando la formula risolutiva scopriamo che questa equazione non ha soluzioni per cui concludiamo che non esiste alcun valore del parametro m per cui l’equazione parametrica sia spuria; ciò vuol dire che non esiste alcuna equazione, tra le infinite equazioni della famiglia parametrica, che ammetta la soluzione nulla. Una soluzione reciproca dell’altra significa che prof. ssa R. Schettino b) Equivale alla condizione , per cui imponendo che il prodotto sia uguale a 1, determiniamo i valori di m tali che le soluzioni siano reciproche : Risolvendo questa equazione di 2° grado nell’incognita m, si determinano ; ciò vuol dire che esistono due valori del parametro, e perciò due equazioni della famiglia parametrica, che ammettono soluzioni reciproche. Quali sono le equazioni e quali le soluzioni reciproche? Riflettere e rispondere. 27

c) La somma dei quadrati delle radici è data dalla penultima formula della tabella per cui imponendo che quella formula sia uguale a 23, determiniamo i valori cercati di m prof. ssa R. Schettino Notiamo che nella nostra equazione la somma delle radici è uguale a m-3 e che il prodotto è uguale a m 2+3 m+3, per cui la condizione richiesta diventa: (m-3)2 -2(m 2+3 m+3)=23 che, risolta, dà i valori m = -2 e m = -10 Ciò vuol dire che esistono due valori di m e quindi due equazioni della famiglia parametrica che ammettono la condizione richiesta dall’esercizio. Anche qui, come si fa a sapere quali equazioni rispettano la richiesta fatta dall’esercizio? N. B. Esercitarsi a decodificare le condizioni richieste dallo studio di equazioni parametriche e sarà più facile determinare i valori del parametro richiesti 28

ALTRI ESEMPI Per quali valori di k l’equazione x 2=k+2 ha due radici reali e distinte? prof. ssa R. Schettino La condizione richiesta equivale alla condizione algebrica > 0 (vedere la tabella), per cui, essendo un’equazione pura imponiamo k + 2 > 0 da cui k> -2 , ciò vuol dire che per tutti i valori di k maggiori di -2 l’equazione corrispondente ammette due radici reali e distinte. Data l’equazione parametrica kx 2 -2(k-1)x+1= 0 determinare i valori di k per cui il prodotto delle radici è 3 La condizione richiesta equivale a ammette la soluzione e l’equazione N. B. Esercitarsi a decodificare le condizioni richieste dallo studio di equazioni parametriche e sarà più facile determinare i valori del parametro richiesti 29