EGR 2201 Unit 11 Sinusoids and Phasors Read

EGR 2201 Unit 11 Sinusoids and Phasors Read Alexander & Sadiku, Chapter 9 and Appendix B. ¡ Homework #11 and Lab #11 due next week. ¡ Quiz next week. ¡

DC Versus AC ¡ In a direct-current (DC) circuit, current flows in one direction only. l ¡ The textbook’s Chapters 1 through 8 cover DC circuits. In an alternating-current (AC) circuit, current periodically reverses direction. l The book’s Chapters 9 through 11 cover AC circuits.

The Math Used in AC Circuits ¡ Our study of AC circuits will rely heavily on two areas of math: l l ¡ Sine and cosine functions Complex numbers We’ll review the math after introducing some terminology used in discussing AC voltages and currents.

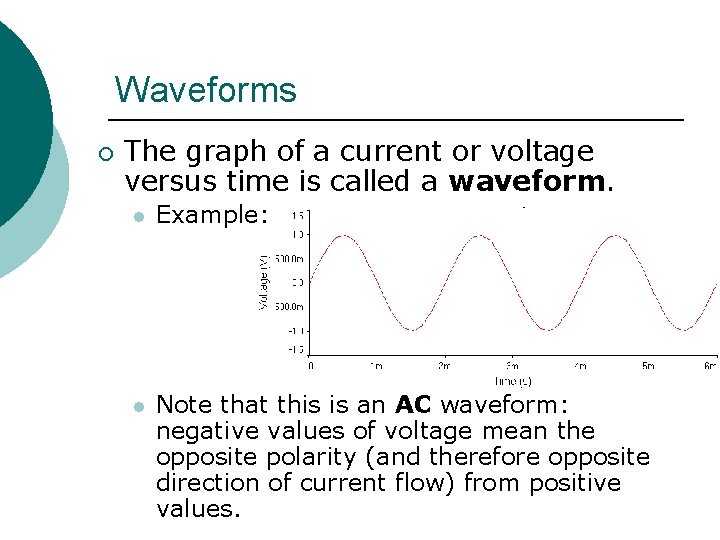
Waveforms ¡ The graph of a current or voltage versus time is called a waveform. l Example: l Note that this is an AC waveform: negative values of voltage mean the opposite polarity (and therefore opposite direction of current flow) from positive values.

Periodic Waveforms ¡ ¡ Often the graph of a voltage or current versus time repeats itself. We call this a periodic waveform. Common shapes for periodic waveforms include: l l ¡ ¡ Sinusoid Square Triangle Sawtooth Image from http: //en. wikipedia. org/wiki/Sinusoids are the most important of these.

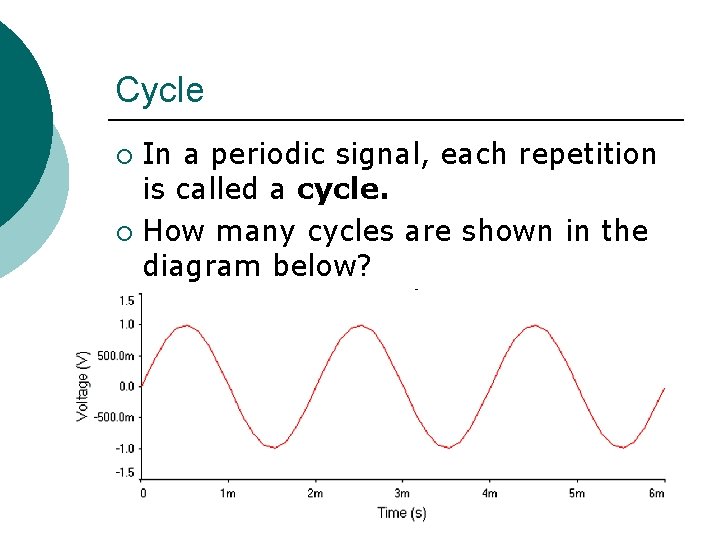
Cycle In a periodic signal, each repetition is called a cycle. ¡ How many cycles are shown in the diagram below? ¡

Waveform Parameters ¡ Important parameters associated with periodic waveforms include: l Period T l Frequency f l Angular Frequency l Amplitude Vm (or Peak Value Vp) l Peak-to-Peak Value l Instantaneous Values

Period The time required for one cycle is called the waveform’s period. ¡ The symbol for period is T. ¡ Period is measured in seconds, abbreviated s. ¡ Example: If a waveform repeats itself every 3 seconds, we’d write T = 3 s ¡

Frequency ¡ ¡ ¡ A waveform’s frequency is the number of cycles that occur in one second. The symbol for frequency is f. Frequency is measured in hertz, abbreviated Hz. l ¡ Some old-timers say “cycles per second” instead of “hertz. ” Example: If a signal repeats itself 20 times every second, we’d write f = 20 Hz

Period and Frequency ¡ ¡ Period and frequency are the reciprocal of each other: f = 1 / T T = 1 / f For practice with these relationships, play my Frequency-Period game.

Radians ¡

Angular Frequency The quantity 2 f, which appears in many equations, is called the angular frequency. ¡ Its symbol is , and its unit is rad/s: = 2 f ¡

One Question, Three Answers So we have three ways of answering the question, “How fast is the voltage (or current) changing? ” 1. Period, T, unit = seconds (s) ¡ l 2. Frequency, f, unit = hertz (Hz) l 3. Tells how many seconds for one cycle. Tells how many cycles per second. Angular frequency, , unit = rad/s l Tells size of angle covered per second, where one complete cycle corresponds to an angle of 2 radians (which is 360 ).

Relating T, f, and If you know any one of these three (period, frequency, angular frequency), you can easily compute the other two. ¡ The key equations that you must memorize are: ¡ T = 1/f = 2 f = 2 /T

Amplitude (or Peak Value) ¡ The maximum value reached by an ac waveform is called its amplitude or peak value.

Peak-to-Peak Value A waveform’s peak-to-peak value is its total height from its lowest value to its highest value. ¡ Many waveforms are symmetric about the horizontal axis. In such cases, the peak-to-peak value is equal to twice the amplitude. ¡

Instantaneous Value The waveform’s instantaneous value is its value at a specific time. ¡ A waveform’s instantaneous value constantly changes, unlike the previous parameters (period, frequency, angular frequency, amplitude, peak-to-peak value), which usually remain constant. ¡

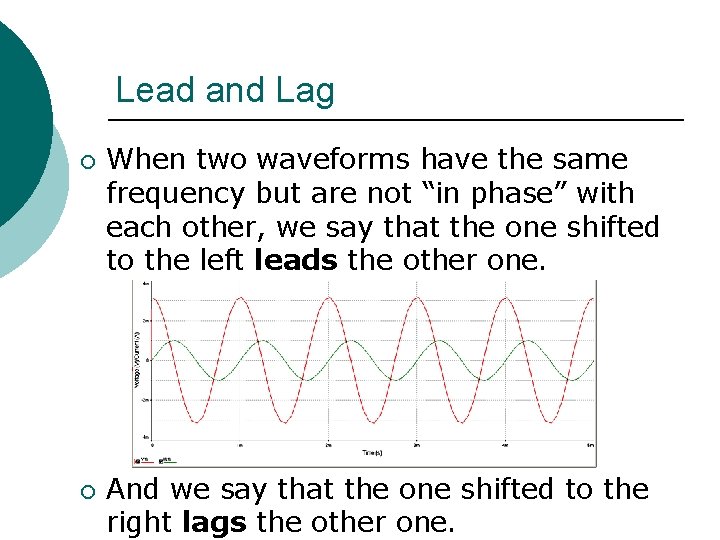
Lead and Lag ¡ ¡ When two waveforms have the same frequency but are not “in phase” with each other, we say that the one shifted to the left leads the other one. And we say that the one shifted to the right lags the other one.

Phase Angle ¡ To quantify the idea of how far a waveform is shifted left or right relative to a reference point, we assign each waveform a phase angle . l ¡ ¡ Recall that one complete cycle corresponds to an angle of 2 radians, or 360. A positive phase angle causes the waveform to shift left along the xaxis. A negative phase angle causes it to shift right.

Sinusoids ¡ ¡ ¡ A sinusoid is a sine wave or a cosine wave or any wave with the same shape, shifted to the left or right. Sinusoids arise in many areas of engineering and science. They are the waveform used most frequently in electrical circuit theory. The waveform we’ve been looking at is a sinusoid.

Amplitude, Frequency, Phase Angle ¡ Any two sinusoids must have the same shape, but can vary in three ways: l l l ¡ Amplitude (maximum value) Angular frequency (how fast the values change) Phase angle (how far shifted to the left or right) We’ll use mathematical expressions for sinusoids that specify these three things….

Mathematical Expression For a Sinusoid ¡ The mathematical expression for a sinusoidal voltage looks like this: v(t) = Vmcos( t + ) ¡ where Vm is the amplitude, is the angular frequency, and is the phase angle (relative to some reference). Example: v(t) = 20 cos(180 t + 30 ) V

Calculator’s Radian Mode and Degree Mode ¡ Recall that when using your calculator’s trig buttons (such as cos), you must pay attention to whether the calculator is in radian mode or degree mode. l l Example: If the calculator is in radian mode, then cos(90) returns 0. 448, which is the cosine of 90 radians. But if the calculator is in degree mode, then cos(90) returns 0, which is the cosine of 90 degrees.

Caution: Radians and Degrees ¡ In the expression for a sinusoid, v(t) = Vmcos( t + ) is usually given in degrees, but is always given in radians per second. ¡ Recommendation: To compute a sinusoid’s instantaneous value, leave your calculator in radian mode, and convert to radians.

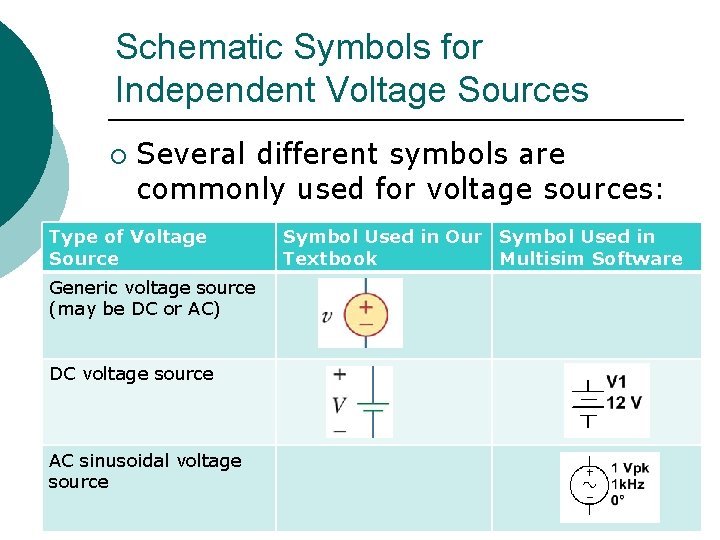
Schematic Symbols for Independent Voltage Sources ¡ Several different symbols are commonly used for voltage sources: Type of Voltage Source Generic voltage source (may be DC or AC) DC voltage source AC sinusoidal voltage source Symbol Used in Our Symbol Used in Textbook Multisim Software

Function Generator ¡ We use a function generator to produce periodic waveforms.

Trainer’s Function Generator Regular Output, controlled by all four knobs. In this course we’ll always use this one. No matter which one of these you use, you must also use the GROUND connection. TTL Mode Output, controlled only by the FREQUENCY and RANGE knobs. Used in Digital Electronics courses.

Oscilloscope We use an oscilloscope to display waveforms. ¡ Using it, we can measure amplitude, period, and phase angle of ac waveforms, as well as dc values, transients, and more. ¡

Oscilloscope Challenge Game The oscilloscope is a complex instrument that you must learn to use. ¡ To learn the basics, play my Oscilloscope Challenge game at ¡ http: //nreeder. com/flashgames. htm.

Sine or Cosine? Any sinusoidal waveform can be expressed mathematically using either the sine function or the cosine function. ¡ Example: these two expressions describe the same waveform: v(t) = 20 sin(300 t + 30 ) v(t) = 20 cos(300 t 60 ) ¡ In a problem where you’re given a mixture of sines and cosines, your first step should be to convert all of the sines to cosines. ¡

Trigonometric Identities Relating Sine and Cosine ¡ ¡ You can convert from sine to cosine (or vice versa) using the trig identities sin(x + 90 ) = cos(x) sin(x 90 ) = cos(x) cos(x + 90 ) = sin(x) cos (x 90 ) = sin(x) These identities reflect the fact that the cosine function leads the sine function by 90.

A Graphical Method Instead of Trig Identities ¡ ¡ ¡ Remembering and applying trig identities may be difficult. The book describes a graphical method that relies on the following diagram: To use it, recall that we measure positive angles counterclockwise, and negative angles clockwise.

Mathematical Review: Complex Numbers ¡ ¡ The system of complex numbers is based on the so-called imaginary unit, which is equal to the square root of 1. Mathematicians use the symbol i for this number, but electrical engineers use j: or

Rectangular versus Polar Form ¡ Any complex number can be expressed in three forms: l Rectangular form ¡ Example: 3 + j 4 l Polar form ¡ Example: 5 53. 1 l Exponential form ¡ Example: 5 e j 53. 1 or 5 e j 0. 927

Rectangular Form ¡ In rectangular form, a complex number z is written as the sum of a real part x and an imaginary part y: z = x + jy

The Complex Plane ¡ We often represent complex numbers as points in the complex plane, with the real part plotted along the horizontal axis (or “real axis”) and the imaginary part plotted along the vertical axis (or “imaginary axis”).

Polar Form ¡ In polar form, a complex number z is written as a magnitude r at an angle : z = r ¡ The angle is measured from the positive real axis.

Converting Between Rectangular and Polar Forms ¡ ¡ We will very often have to convert from rectangular form to polar form, or vice versa. This is easy to do if you remember a bit of right-angle trigonometry.

Converting from Rectangular Form to Polar Form ¡ Given a complex number z with real part x and imaginary part y, its magnitude is given by and its angle is given by

Inverse Tangent Button on Your Calculator When using your calculator’s tan 1 (inverse tangent) button, pay attention to whether the calculator is in degree mode or radian mode. Also recall that the calculator’s answer may be in the wrong quadrant, and that you may need to adjust the answer by 180. ¡ ¡ l The tan 1 button always returns an angle in Quadrants I or IV, even if you want an answer in Quadrants II or III.

Converting from Polar Form to Rectangular Form ¡ Given a complex number z with magnitude r and angle , its real part is given by and its imaginary part is given by

Exponential Form ¡ Complex numbers may also be written in exponential form. Think of this as a mathematically respectable version of polar form. Polar form Exponential Form r Example: ¡ 3 30 rej 3 ej /6 In exponential form, should be in radians.

Euler’s Identity ¡ The exponential form is based on Euler’s identity, which says that, for any ,

Mathematical Operations ¡ You must be able to perform the following operations on complex numbers: l l l Addition Subtraction Multiplication Division Complex Conjugate

Addition ¡ ¡ Adding complex numbers is easiest if the numbers are in rectangular form. Suppose z 1 = x 1+jy 1 and z 2 = x 2+jy 2 Then z 1 + z 2 = (x 1+x 2) + j(y 1+y 2) ¡ In words: to add two complex numbers in rectangular form, add their real parts to get the real part of the sum, and add their imaginary parts to get the imaginary part of the sum.

Subtraction ¡ ¡ Subtracting complex numbers is also easiest if the numbers are in rectangular form. Suppose z 1 = x 1+jy 1 and z 2 = x 2+jy 2 Then z 1 z 2 = (x 1 x 2) + j(y 1 y 2) ¡ In words: to subtract two complex numbers in rectangular form, subtract their real parts to get the real part of the result, and subtract their imaginary parts to get the imaginary part of the result.

Multiplication ¡ ¡ Multiplying complex numbers is easiest if the numbers are in polar form. Suppose z 1 = r 1 1 and z 2 = r 2 2 Then z 1 z 2 = (r 1 r 2) ( 1+ 2) ¡ In words: to multiply two complex numbers in polar form, multiply their magnitudes to get the magnitude of the result, and add their angles to get the angle of the result.

Division ¡ ¡ Dividing complex numbers is also easiest if the numbers are in polar form. Suppose z 1 = r 1 1 and z 2 = r 2 2 Then z 1 ÷ z 2 = (r 1 ÷ r 2) ( 1 2) ¡ In words: to divide two complex numbers in polar form, divide their magnitudes to get the magnitude of the result, and subtract their angles to get the angle of the result.

Complex Conjugate ¡ ¡ Given a complex number in rectangular form, z = x + jy its complex conjugate is simply z* = x jy Given a complex number in polar form, z = r its complex conjugate is simply z* = r

Performing Complicated Operations on Complex Numbers ¡

Entering Complex Numbers in MATLAB ¡ Entering a number in rectangular form: >> z 1 = 3 + j 4 ¡ Entering a number in polar (actually, exponential) form: >> z 5 = 3 exp(j − 30 pi / 180) ¡ ¡ You must give the angle in radians, not degrees. MATLAB always displays complex numbers in rectangular form, no matter how you enter them.

Operating on Complex Numbers in MATLAB ¡ Use the usual mathematical operators for addition, subtraction, multiplication, division: >> z 8 = z 1 + z 5 ¡ >> z 9 = z 5 / z 6 and so on.

Built-In Complex Functions in MATLAB Useful MATLAB functions: ¡ l l l ¡ real(z 1) gives z 1’s real part imag(z 1) gives z 1’s imaginary part abs(z 1) gives z 1’s magnitude angle(z 1) gives z 1’s angle in radians conj(z 1) gives z 1’s complex conjugate Since angle(z 1) gives you the angle in radians, you must multiply this by 180/pi if you want the angle in degrees.

Online Alternative to MATLAB ¡ Recall that wolframalpha. com is a free online math tool. An earlier example in MATLAB: Same example in Wolfram. Alpha: >> z 1 = 3 + j 4 >> z 5 = 3 exp(j − 30 pi / 180) >> z 8 = z 1 + z 5 >> abs(z 8) >> angle(z 8) 180 / pi Note that you must use i rather than j for the imaginary unit. Next slide shows results of this command.

Online Alternative to MATLAB (cont'd. ) ¡ Rect. form Polar form Here is part of the result of the previous command in wolframalpha. com:

Reminder About Calculators ¡ ¡ ¡ In this course I’ll let you use any calculator or MATLAB on the exams. But the Fundamentals of Engineering exam and the Principles and Practice of Engineering exam have a restrictive calculator policy. To succeed on those exams, you must be able to do complex-number math with a “bare-bones” calculator.

Useful Properties of j ¡

Sinusoids Everywhere ¡ If you connect a sinusoidal voltage source or current source to a circuit made up of resistors, capacitors, and inductors, then: 1. 2. ¡ Every voltage and every current in the circuit will also be a sinusoid. All of these sinusoids will have the same frequency. Statement #1 is not true for sources of other waveshapes, such as triangle waves, square waves, or sawtooth waves.

Kirchhoff’s Laws in AC Circuits ¡ ¡ KCL and KVL hold in AC circuits. But to apply these laws, we must add (or subtract) sinusoids instead of adding (or subtracting) numbers. l Example: In the circuit shown, KVL tells us that v = v 1 + v 2. Suppose that v 1 = 10 cos(200 t + 30 ) V and v 2 = 4 cos(200 t + 90 ) V How can we add those to find v?

Adding Sinusoids We often need to find the sum of two or more sinusoids. ¡ A unique mathematical property of sinusoids: the sum of sinusoids of the same frequency is always another sinusoid of that frequency. ¡ You can’t make the same statement for triangle waves, square waves, sawtooth waves, or other waveshapes. ¡

Adding Sinusoids (Continued) ¡ For example, if we add v 1 = 10 cos(200 t + 30 ) V + v 2 = 4 cos(200 t + 90 ) V we’re guaranteed to get another sinusoid of the same angular frequency, 200 rad/s: v 1 + v 2 = Vm cos(200 t + ) V ¡ But how do we figure out the resulting sinusoid’s amplitude Vm and phase angle ?

Adding Sinusoids: A Common Mistake ¡ Here’s a common beginner mistake that is sure to give you the wrong answer: v 1 = 10 cos(200 t + 30 ) V + v 2 = 4 cos(200 t + 90 ) V v 1 + v 2 = 14 cos(400 t + 120 ) V

Using MATLAB to Plot the Sinusoids That We’re Adding ¡ ¡ We have v 1 = 10 cos(200 t + 30 ) V v 2 = 4 cos(200 t + 90 ) V and we’re trying to find v 1 + v 2. In MATLAB: >> fplot('10 * cos(200 * t + pi/6)', [0, 0. 1]) >> hold on >> fplot('4 * cos(200 * t + pi/2)', [0, 0. 1], 'r') >> fplot('10*cos(200*t + pi/6) + 4*cos(200*t + pi/2)', [0, 0. 1], 'g')

Complex Numbers to the Rescue! ¡ One method for adding sinusoids relies on trig identities. l ¡ You learned this method if you took the course named Introductory Math for Engineering Applications (EGR 1101). But we’ll use a simpler method, which relies on complex numbers. l In fact, the only reason we’re interested in complex numbers (in this course) is that they give us a simple way to add and subtract sinusoids.

Phasors ¡ ¡ ¡ A phasor is a complex number that represents the amplitude and phase angle of a sinusoidal voltage or current. The phasor’s magnitude r is equal to the sinusoid’s amplitude. The phasor’s angle is equal to the sinusoid’s phase angle. l Example: To represent the sinusoid v(t) = 10 cos(200 t + 30 ) V we’ll use the phasor V = 10 30 V

Time Domain and Phasor Domain Some fancy terms: ¡ We call an expression like 10 cos(200 t + 30 ) V the time-domain representation of a sinusoid. ¡ We call 10 30 V the phasor-domain representation of the same sinusoid. (It’s also called the frequency-domain representation. ) ¡

Using Phasors to Add Sinusoids To add sinusoids of the same frequency: 1. If any of your sinusoids are expressed using sine, convert them all to cosine. 2. Write the phasor-domain version of each sinusoid. 3. Add the phasors (which are just complex numbers). 4. Write the time-domain version of the resulting phasor. ¡

Example of Using Phasors to Add Sinusoids To add v 1 = 10 cos(200 t + 30 ) V + v 2 = 4 cos(200 t + 90 ) V ¡ Transform from time domain to phasor domain: V 1 = 10 30 V and V 2 = 4 90 V ¡ ¡ ¡ Add the phasors: V 1 + V 2 = 10 30 + 4 90 = 12. 49 46. 1 V Transform from phasor domain back to time domain: v 1 + v 2 = 12. 49 cos(200 t + 46. 1 ) V

Phasor Relationships for Circuit Elements We’ve seen how we can use phasors to add sinusoids. ¡ Next we’ll revisit the voltage-current relationships for resistors, inductors, and capacitors, assuming that their voltages and currents are sinusoids. ¡

Phasor Relationship for Resistors ¡ For resistors we have, in the time domain: v = i. R l l l Example: If i = 2 cos(200 t + 30 ) A and R = 5 , then v = 10 cos(200 t + 30 ) V For this same example, in the phasor domain we have: If I = 2 30 A and R = 5 , then V = 10 30 V So we can write V = IR.

What This Means For resistors, if i is a sinusoid, then v will be a sinusoid with the same frequency and phase angle as i. ¡ Therefore i and v reach their peak values at the same instant. ¡ We say that a resistor’s voltage and current are in phase. ¡

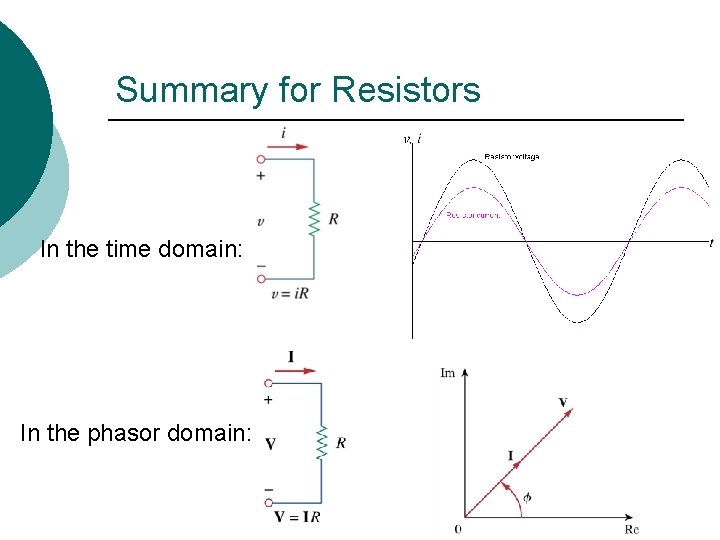
Summary for Resistors In the time domain: In the phasor domain:

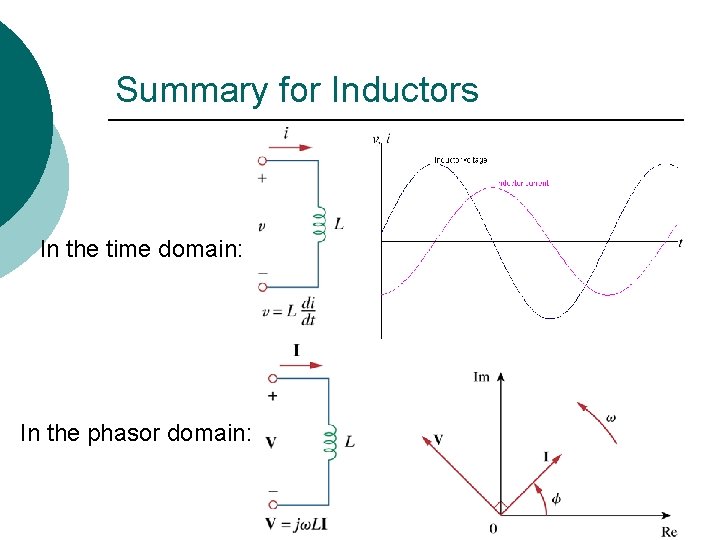
Phasor Relationship for Inductors ¡

What This Means ¡ For inductors, if i is a sinusoid, then v will be a sinusoid with the same frequency as i, but i will lag v by 90.

Summary for Inductors In the time domain: In the phasor domain:

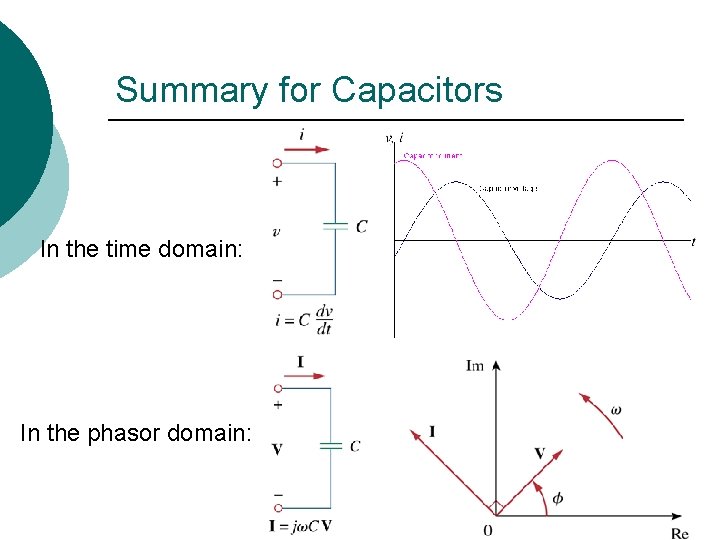
Phasor Relationship for Capacitors ¡

What This Means ¡ For capacitors, if i is a sinusoid, then v will be a sinusoid with the same frequency as i, but i will lead v by 90.

Summary for Capacitors In the time domain: In the phasor domain:

Summary: Textbook’s Table 9. 2 ¡ Working in the frequency domain (phasor domain) is nicer than working in the time domain because we can use algebra instead of calculus and differential equations.

A Memory Aid ¡ To remember whether current leads or lags voltage in a capacitor or inductor, remember the phrase “ELI the ICEman” ¡ (For this to make sense, you must know that E is sometimes used as the abbreviation for voltage. )

Impedance ¡

A Resistor’s Impedance ¡

Resistors and Frequency A resistor’s impedance does not depend on frequency, since Z=R for a resistor. ¡ Therefore, a resistor doesn’t oppose high-frequency current any more or less than it opposes low-frequency current. ¡

An Inductor’s Impedance ¡

Inductors and Frequency The magnitude of an inductor’s impedance is directly proportional to frequency, since Z = j L for an inductor. ¡ Therefore, an inductor opposes high -frequency current more than it opposes low-frequency current. ¡ Also, as 0, Z 0, which is why inductors act like short circuits in dc circuits. ¡

A Capacitor’s Impedance ¡

Capacitors and Frequency ¡

Summary: Impedances of the Basic Elements Ignore this column for now.

Ohm’s Law Generalized ¡

A Typical AC Circuit Problem ¡ ¡ Suppose we want to find i(t) in this circuit. Here are the steps: 1. 2. 3. 4. Transform to the phasor domain (i. e. , write the voltage source in phasor form Vs and find the resistor’s impedance ZR and the capacitor’s impedance ZC). Combine ZR and ZC to find the circuit’s total impedance Zeq. (See next slide. ) Apply Ohm’s law: I = Vs ÷ Zeq. Transform back to the time domain by converting I to i(t).

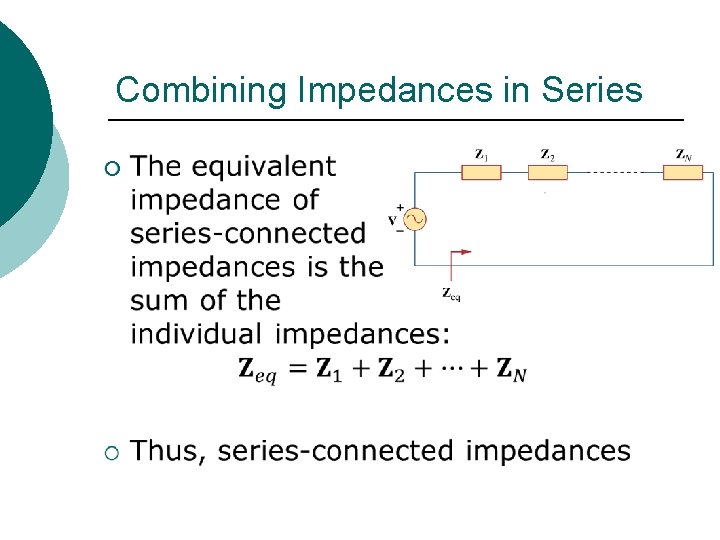
Combining Impedances in Series ¡

Combining Impedances in Parallel ¡

Voltage-Divider Rule ¡

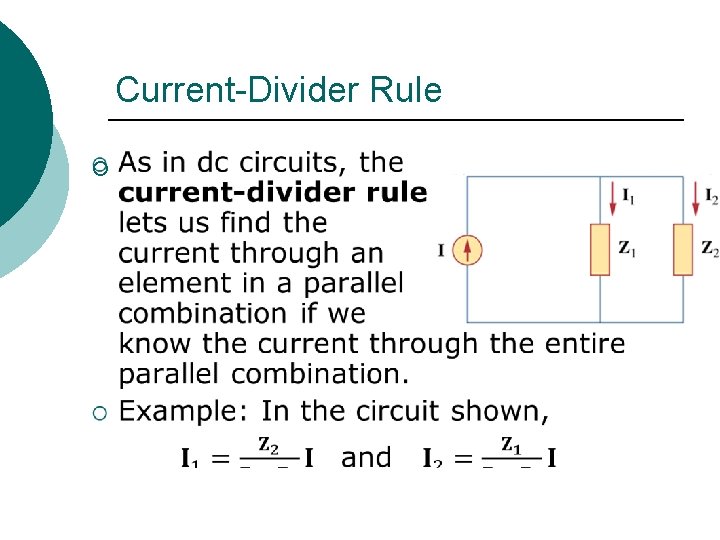
Current-Divider Rule ¡

Summary of Chapter 9 ¡

What’s Next? ¡ In Chapter 10 we’ll see that we can also apply these other familiar techniques in the phasor domain: l l l Nodal analysis Mesh analysis Superposition Source transformation Thevenin’s theorem Norton’s theorem

General Procedure for Analyzing AC Circuits with Sinusoidal Sources 1. 2. 3. Transform the circuit from the time domain to the phasor domain. Solve the problem using circuit techniques (Ohm’s law, Kirchhoff’s laws, voltage-divider rule, mesh analysis, etc. ). This will involve doing math with complex numbers instead of real numbers. Transform the resulting phasor to the time domain.

Terminology: Impedance, Resistance, and Reactance ¡

Impedance, Resistance, and Reactance of Single Elements Element Impedance Resistance Reactance Resistor R R Inductor j L L Capacitor ¡ Inductors and capacitors are called reactive elements because they have reactance but no resistance.

Admittance ¡ ¡ ¡ Recall that the reciprocal of resistance is called conductance, abbreviated G: G=1/R The reciprocal of impedance is called admittance, abbreviated Y: Y=1/Z Conductance and admittance are measured in siemens (S).

More Terminology: Admittance, Conductance, and Susceptance ¡

Admittance, Conductance, and Susceptance of Single Elements Element Resistor Admittance Conductance Susceptance G Inductor Capacitor G j C