Efficiently Solving Convex Relaxations for MAP Estimation M

Efficiently Solving Convex Relaxations for MAP Estimation M. Pawan Kumar University of Oxford Philip Torr Oxford Brookes University

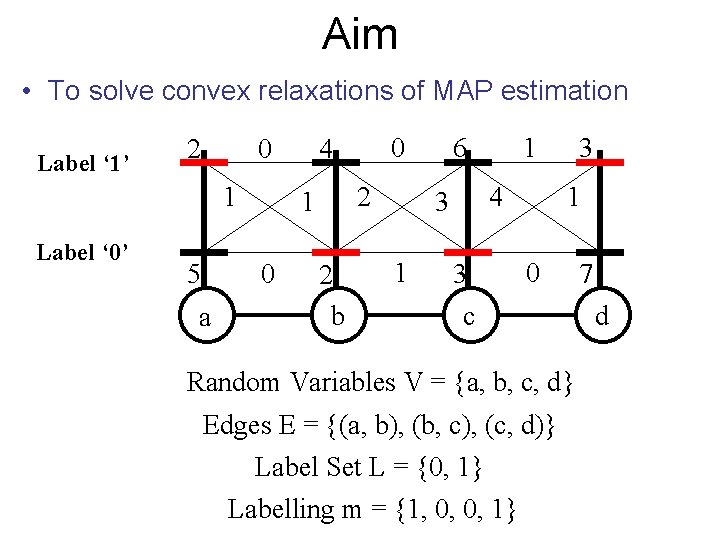
Aim • To solve convex relaxations of MAP estimation Label ‘ 1’ 2 0 1 Label ‘ 0’ 5 a 2 1 0 0 4 2 b 6 4 3 1 1 3 3 1 0 c Random Variables V = {a, b, c, d} Edges E = {(a, b), (b, c), (c, d)} Label Set L = {0, 1} Labelling m = {1, 0, 0, 1} 7 d

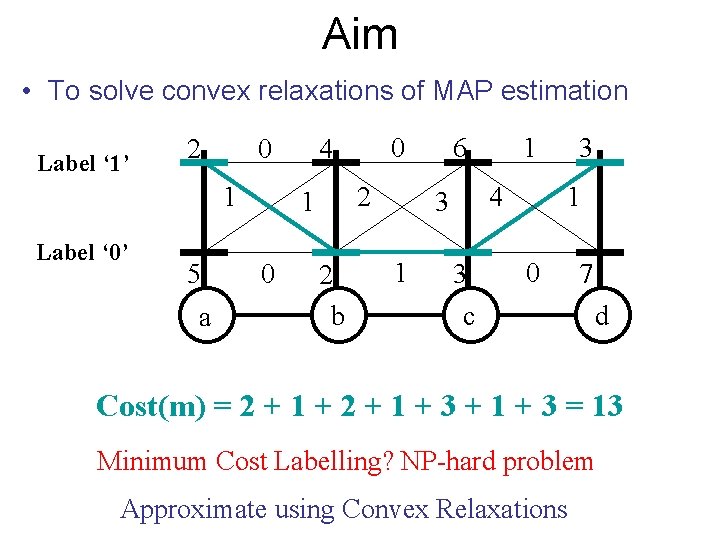
Aim • To solve convex relaxations of MAP estimation Label ‘ 1’ 2 0 1 Label ‘ 0’ 5 a 2 1 0 0 4 2 b 6 4 3 1 1 3 3 1 0 c 7 d Cost(m) = 2 + 1 + 3 = 13 Minimum Cost Labelling? NP-hard problem Approximate using Convex Relaxations

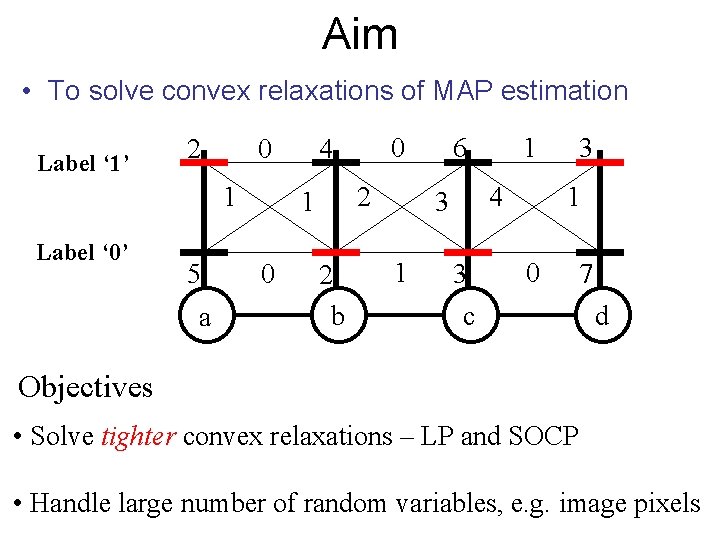
Aim • To solve convex relaxations of MAP estimation Label ‘ 1’ 2 0 1 Label ‘ 0’ 5 a 2 1 0 0 4 2 b 6 4 3 1 1 3 3 1 0 c 7 d Objectives • Solve tighter convex relaxations – LP and SOCP • Handle large number of random variables, e. g. image pixels

Outline • Integer Programming Formulation • Linear Programming Relaxation • Additional Constraints • Solving the Convex Relaxations • Results and Conclusions

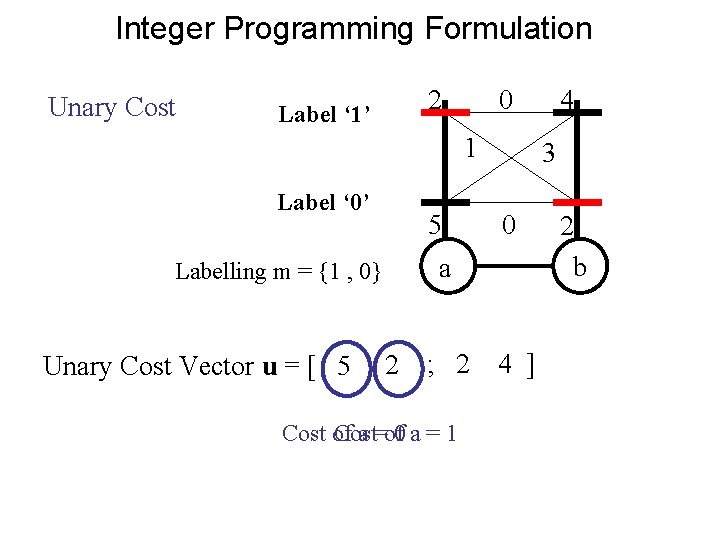
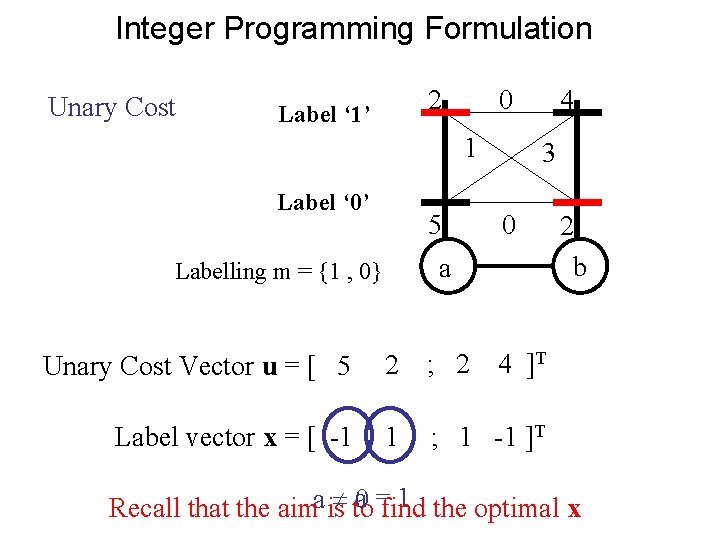
Integer Programming Formulation Unary Cost 2 Label ‘ 1’ 0 1 Label ‘ 0’ 5 Unary Cost Vector u = [ 5 3 0 a Labelling m = {1 , 0} 2 ; 2 Cost of Cost a =of 0 a = 1 4 4 ] 2 b

Integer Programming Formulation Unary Cost 2 Label ‘ 1’ 0 1 Label ‘ 0’ 5 4 3 0 a Labelling m = {1 , 0} Unary Cost Vector u = [ 5 2 ; 2 Label vector x = [ -1 1 ; 1 -1 ]T 2 b 4 ]T 1 the optimal x 0 a =find Recall that the aima is to

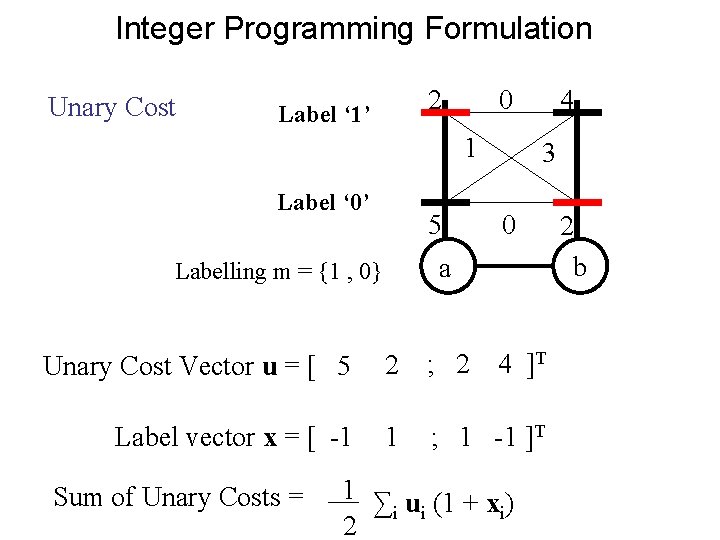
Integer Programming Formulation Unary Cost 2 Label ‘ 1’ 0 1 Label ‘ 0’ 5 4 3 0 a Labelling m = {1 , 0} Unary Cost Vector u = [ 5 2 ; 2 Label vector x = [ -1 1 ; 1 -1 ]T Sum of Unary Costs = 4 ]T 1 ∑ u (1 + x ) i i i 2 2 b

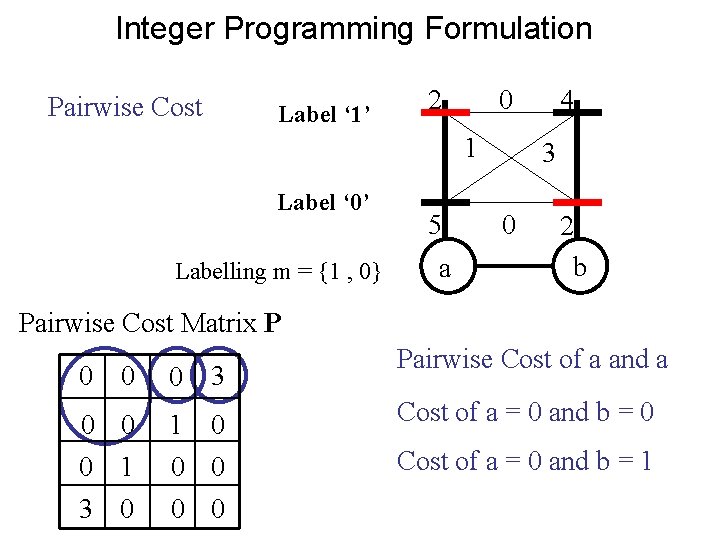
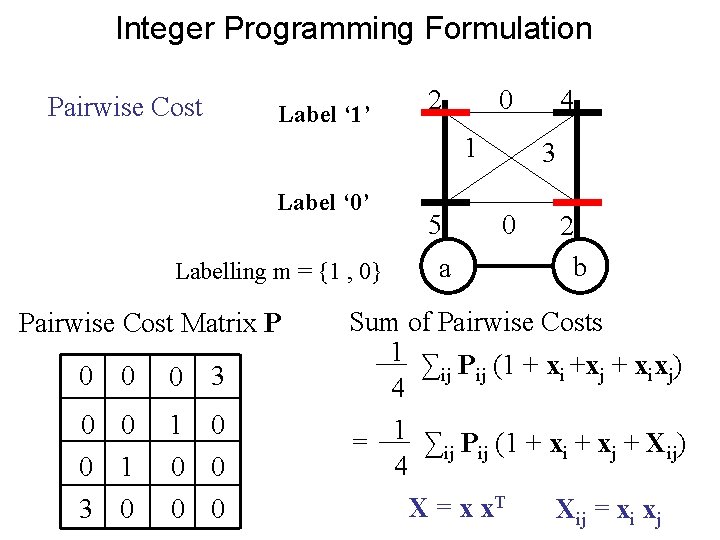
Integer Programming Formulation Pairwise Cost Label ‘ 1’ 2 0 1 Label ‘ 0’ Labelling m = {1 , 0} 5 a 4 3 0 2 b Pairwise Cost Matrix P 0 0 0 3 0 0 0 1 1 0 0 0 3 0 0 0 Pairwise Cost of a and a Cost of a = 0 and b = 0 Cost of a = 0 and b = 1

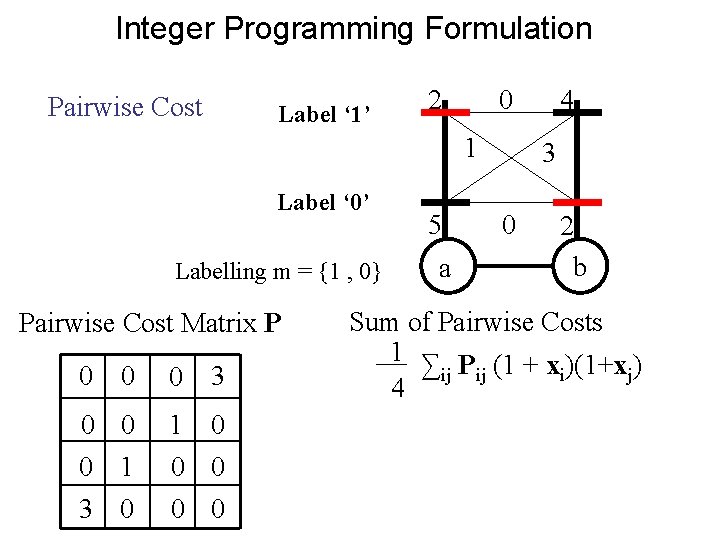
Integer Programming Formulation Pairwise Cost Label ‘ 1’ 2 0 1 Label ‘ 0’ Labelling m = {1 , 0} Pairwise Cost Matrix P 0 0 0 3 0 0 0 1 1 0 0 0 3 0 0 0 5 a 4 3 0 2 b Sum of Pairwise Costs 1 ∑ P (1 + x )(1+x ) ij ij i j 4

Integer Programming Formulation Pairwise Cost Label ‘ 1’ 2 0 1 Label ‘ 0’ Labelling m = {1 , 0} Pairwise Cost Matrix P 0 0 0 3 0 0 0 1 1 0 0 0 3 0 0 0 5 a 4 3 0 2 b Sum of Pairwise Costs 1 ∑ P (1 + x +x + x x ) ij ij i j 4 = 1 ∑ij Pij (1 + xi + xj + Xij) 4 X = x x. T Xij = xi xj

Integer Programming Formulation Constraints • Integer Constraints xi {-1, 1} X = x x. T • Uniqueness Constraint ∑ xi = 2 - |L| i a

Integer Programming Formulation x* = argmin 1 ∑ u (1 + x ) + 1 ∑ P (1 + x + X ) ij i j ij i i 4 2 ∑ xi = 2 - |L| i a Convex xi {-1, 1} X = x x. T Non-Convex

Outline • Integer Programming Formulation • Linear Programming Relaxation • Additional Constraints • Solving the Convex Relaxations • Results and Conclusions

Linear Programming Relaxation Schlesinger, 1976 Retain Convex Part x* = argmin 1 ∑ u (1 + x ) + 1 ∑ P (1 + x + X ) ij i j ij i i 4 2 ∑ xi = 2 - |L| i a xi {-1, 1} X = x x. T

Linear Programming Relaxation Schlesinger, 1976 Retain Convex Part x* = argmin 1 ∑ u (1 + x ) + 1 ∑ P (1 + x + X ) ij i j ij i i 4 2 ∑ xi = 2 - |L| i a xi [-1, 1] Xij [-1, 1] 1 + xi + xj + Xij ≥ 0 ∑ Xij = (2 - |L|) xi j b

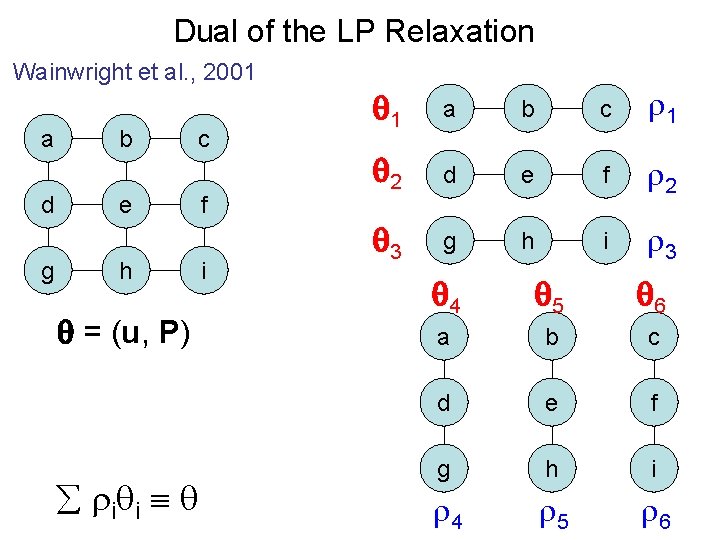
Dual of the LP Relaxation Wainwright et al. , 2001 a d g b c e h = (u, P) i i f i 1 a b c 1 2 d e f 2 3 g h i 3 4 5 6 a b c d e f g h i 4 5 6

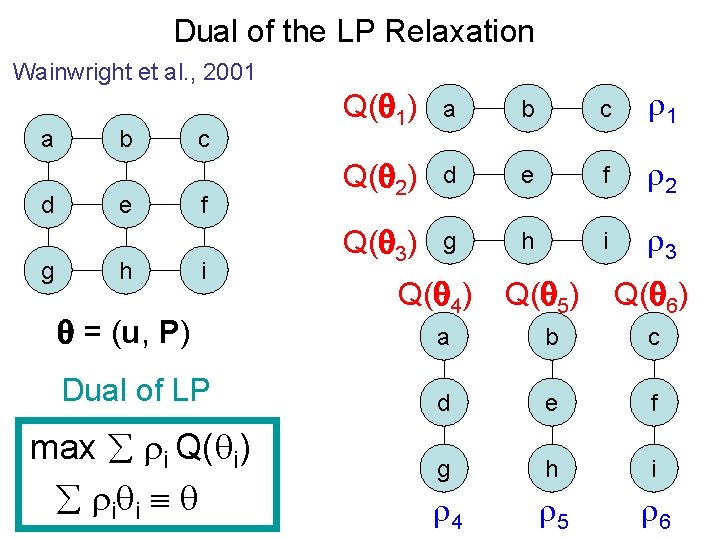
Dual of the LP Relaxation Wainwright et al. , 2001 a d g b e h c f i = (u, P) Dual of LP max i Q( i) i i Q( 1) a b c 1 Q( 2) d e f 2 Q( 3) g h i 3 Q( 4) Q( 5) Q( 6) a b c d e f g h i 4 5 6

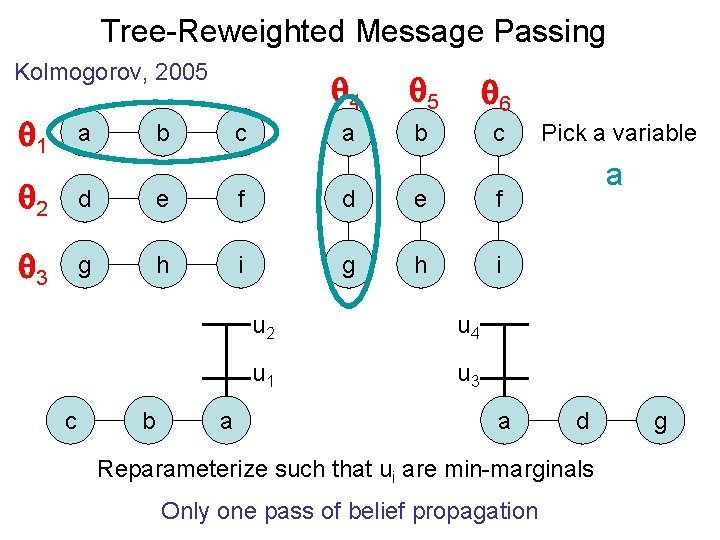
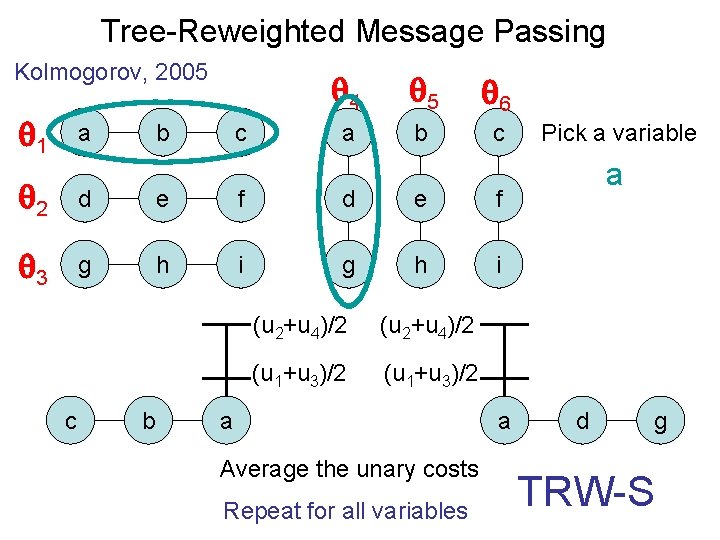
Tree-Reweighted Message Passing Kolmogorov, 2005 4 5 6 a b c 1 a 2 d e f 3 g h i c b b c a u 2 u 4 u 1 u 3 a Pick a variable a d Reparameterize such that ui are min-marginals Only one pass of belief propagation g

Tree-Reweighted Message Passing Kolmogorov, 2005 4 5 6 a b c 1 a 2 d e f 3 g h i c b b c (u 2+u 4)/2 (u 1+u 3)/2 a Average the unary costs Repeat for all variables a Pick a variable a d g TRW-S

Outline • Integer Programming Formulation • Linear Programming Relaxation • Additional Constraints • Solving the Convex Relaxations • Results and Conclusions

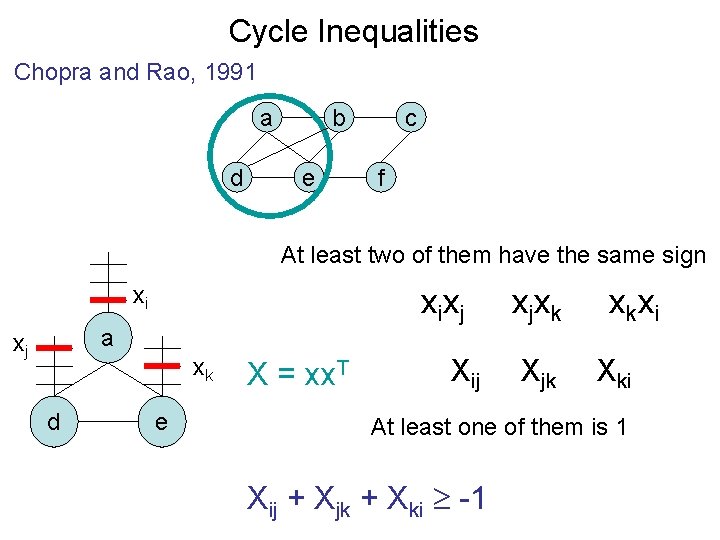
Cycle Inequalities Chopra and Rao, 1991 a d b e c f At least two of them have the same sign xi xixj a xj xk d e X = xx. T Xij xjxk Xjk xkxi Xki At least one of them is 1 Xij + Xjk + Xki -1

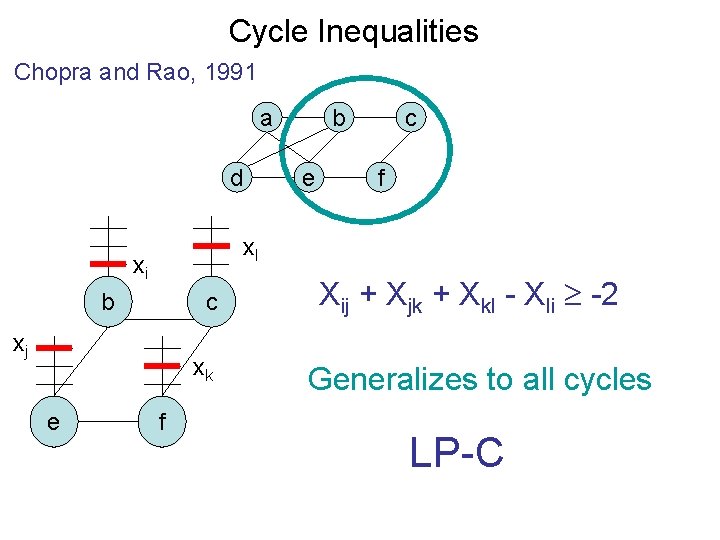
Cycle Inequalities Chopra and Rao, 1991 a d e c f xl xi b c xj xk e b f Xij + Xjk + Xkl - Xli -2 Generalizes to all cycles LP-C

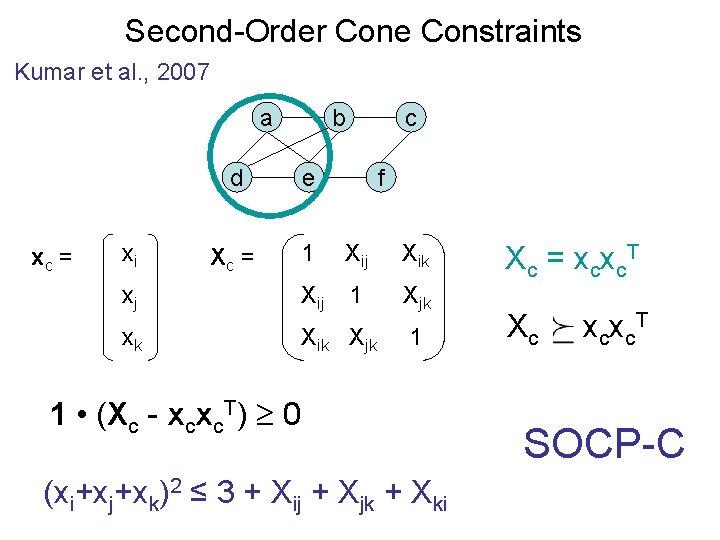
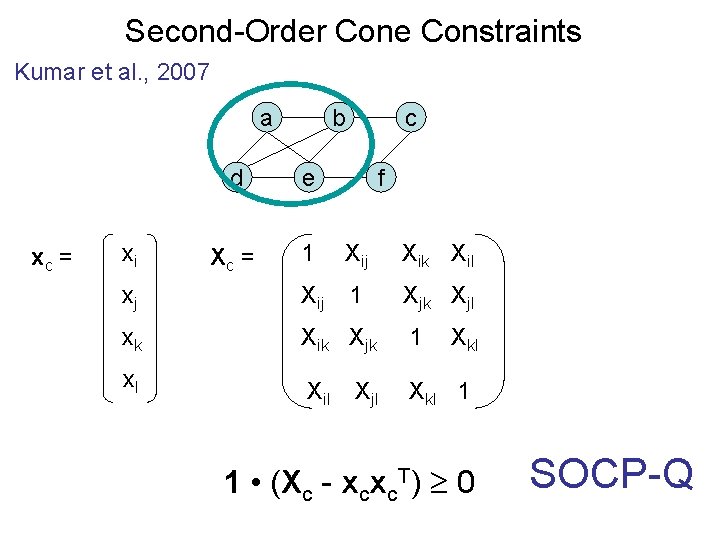
Second-Order Cone Constraints Kumar et al. , 2007 a xc = b c d e Xc = 1 Xij Xik xj Xij 1 Xjk xk Xik Xjk xi f 1 1 • (Xc - xcxc. T) 0 (xi+xj+xk)2 ≤ 3 + Xij + Xjk + Xki Xc = xcxc. T Xc xcxc. T SOCP-C

Second-Order Cone Constraints Kumar et al. , 2007 a xc = b c d e Xc = 1 Xij Xik Xil xj Xij 1 Xjk Xjl xk Xik Xjk 1 xl Xil Xkl 1 xi f Xjl Xkl 1 • (Xc - xcxc. T) 0 SOCP-Q

Outline • Integer Programming Formulation • Linear Programming Relaxation • Additional Constraints • Solving the Convex Relaxations • Results and Conclusions

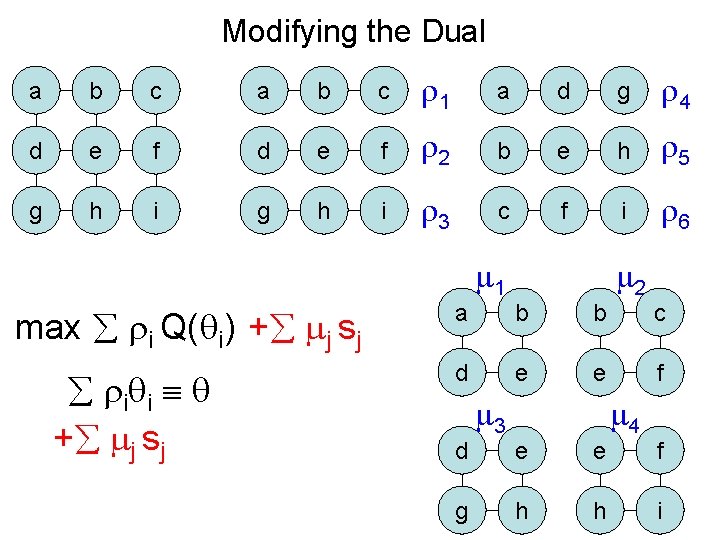
Modifying the Dual a b c 1 a d g 4 d e f 2 b e h 5 g h i 3 c f i 6 max i Q( i) + j sj i i + j sj a 1 d d g 3 b b e e h h 2 c f 4 f i

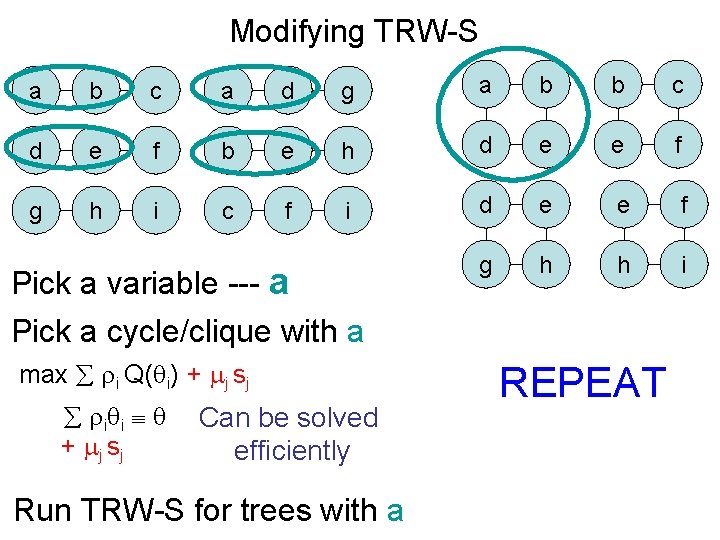
Modifying TRW-S a b c a d g a b b c d e f b e h d e e f g h i c f i d e e f g h h i Pick a variable --- a Pick a cycle/clique with a max i Q( i) + j sj i i + j sj Can be solved efficiently Run TRW-S for trees with a REPEAT

Properties of the Algorithm satisfies the reparametrization constraint Value of dual never decreases CONVERGENCE Solution satisfies Weak Tree Agreement (WTA) WTA not sufficient for convergence More accurate results than TRW-S

Outline • Integer Programming Formulation • Linear Programming Relaxation • Additional Constraints • Solving the Convex Relaxations • Results and Conclusions

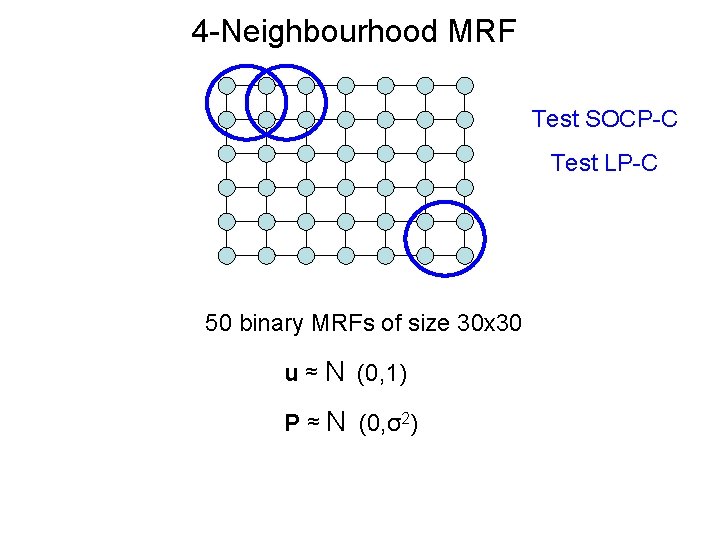
4 -Neighbourhood MRF Test SOCP-C Test LP-C 50 binary MRFs of size 30 x 30 u ≈ N (0, 1) P ≈ N (0, σ2)

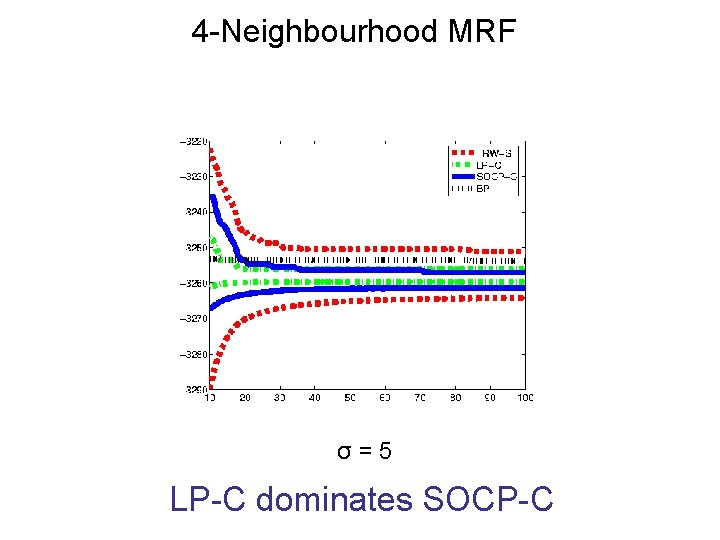
4 -Neighbourhood MRF σ=5 LP-C dominates SOCP-C

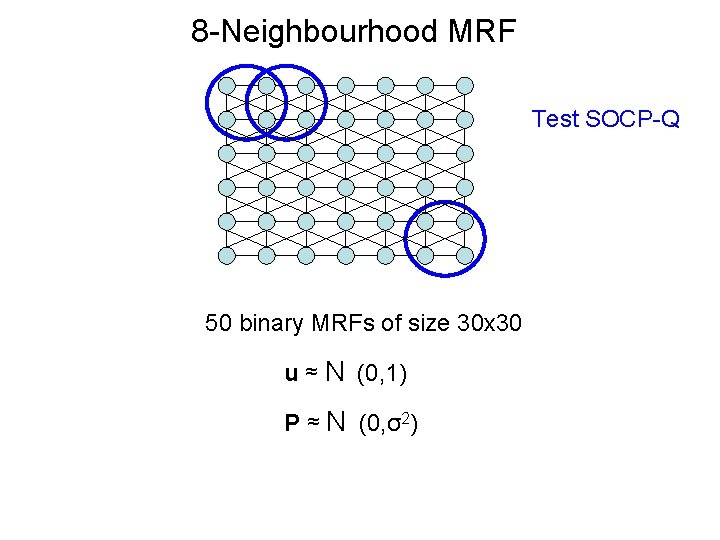
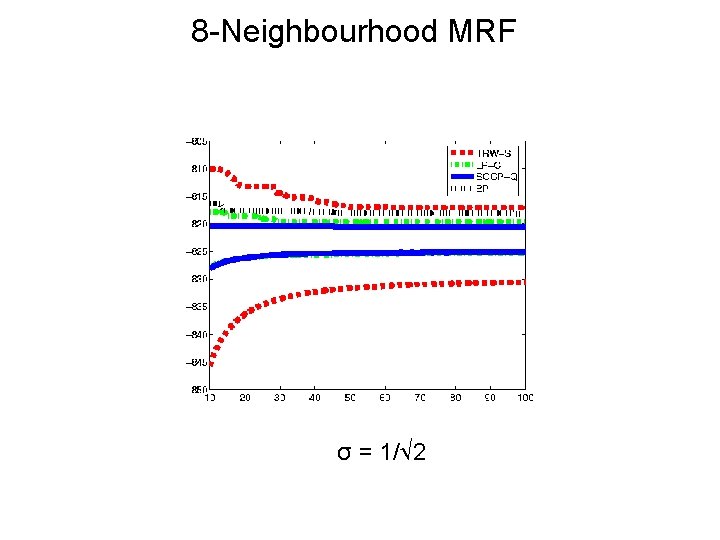
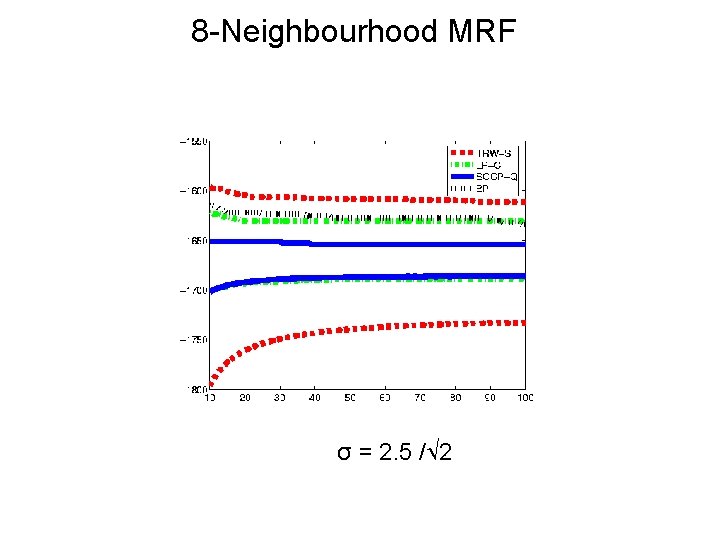
8 -Neighbourhood MRF Test SOCP-Q 50 binary MRFs of size 30 x 30 u ≈ N (0, 1) P ≈ N (0, σ2)

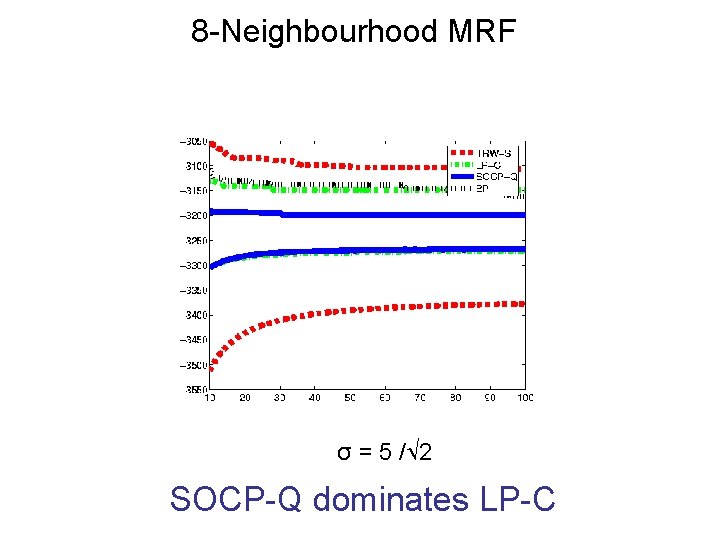
8 -Neighbourhood MRF σ = 5 / 2 SOCP-Q dominates LP-C

Conclusions • Modified LP dual to include more constraints • Extended TRW-S to solve tighter dual • Experiments show improvement • More results in the poster

Future Work • More efficient subroutines for solving cycles/cliques • Using more accurate LP solvers proximal projections • Analysis of SOCP-C vs. LP-C

Questions?

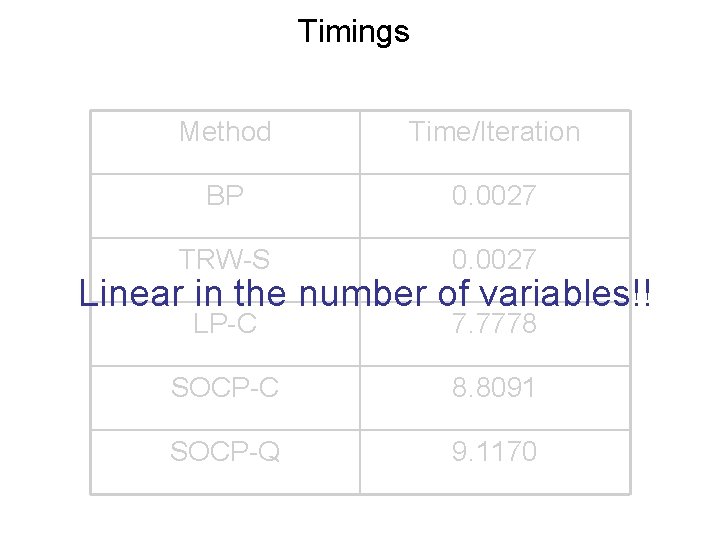
Timings Method Time/Iteration BP 0. 0027 TRW-S 0. 0027 LP-C 7. 7778 SOCP-C 8. 8091 SOCP-Q 9. 1170 Linear in the number of variables!!

Video Segmentation Keyframe User Segmentation Segment remaining video ….

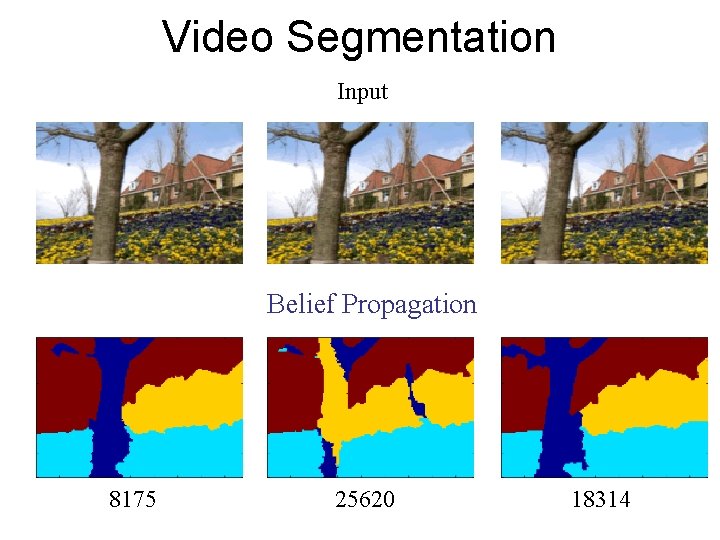
Video Segmentation Input Belief Propagation 8175 25620 18314

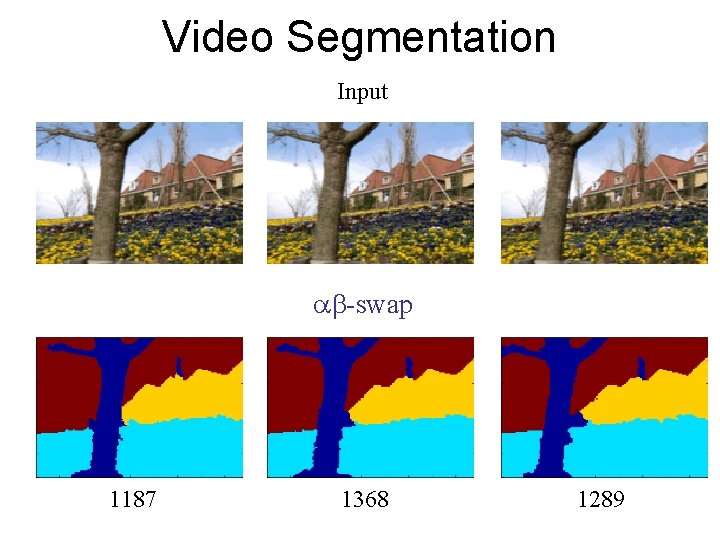
Video Segmentation Input -swap 1187 1368 1289

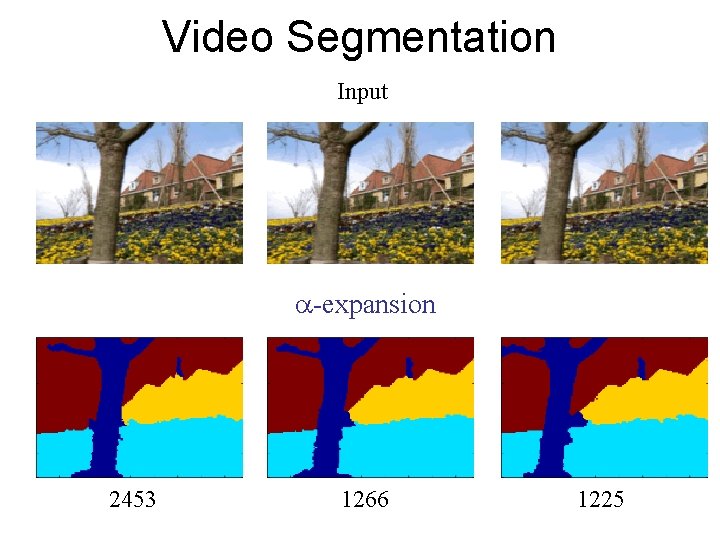
Video Segmentation Input -expansion 2453 1266 1225

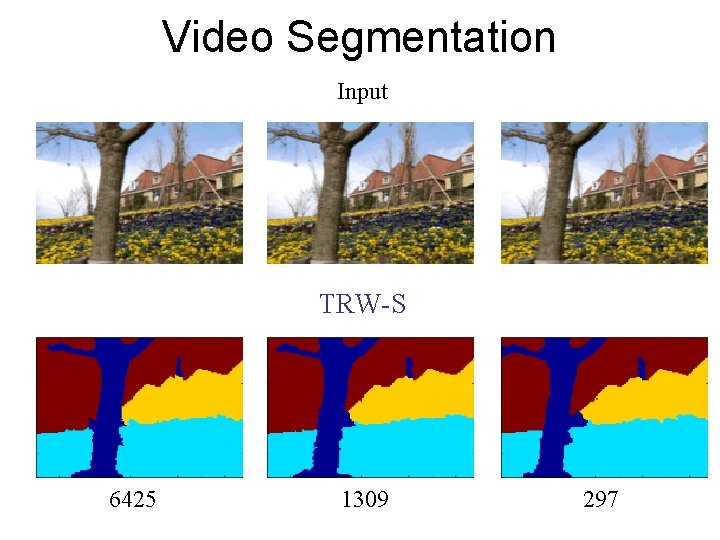
Video Segmentation Input TRW-S 6425 1309 297

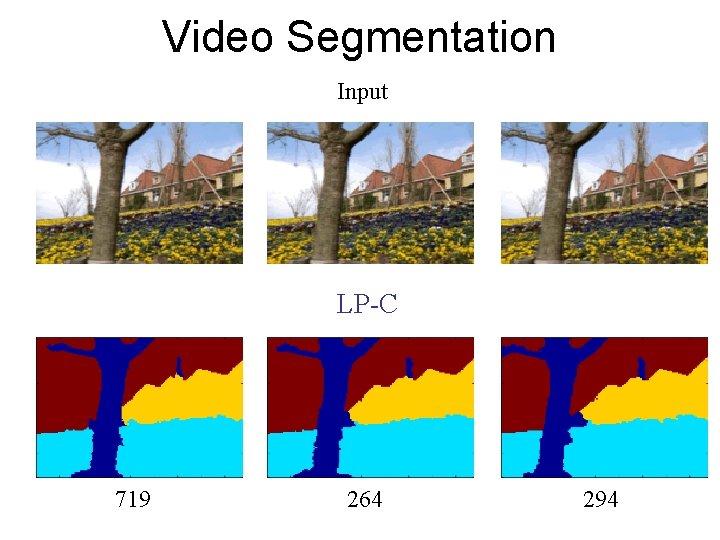
Video Segmentation Input LP-C 719 264 294

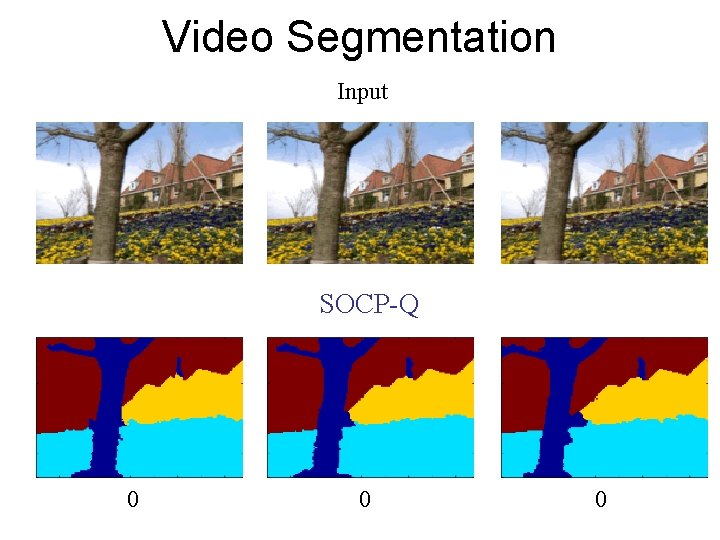
Video Segmentation Input SOCP-Q 0 0 0

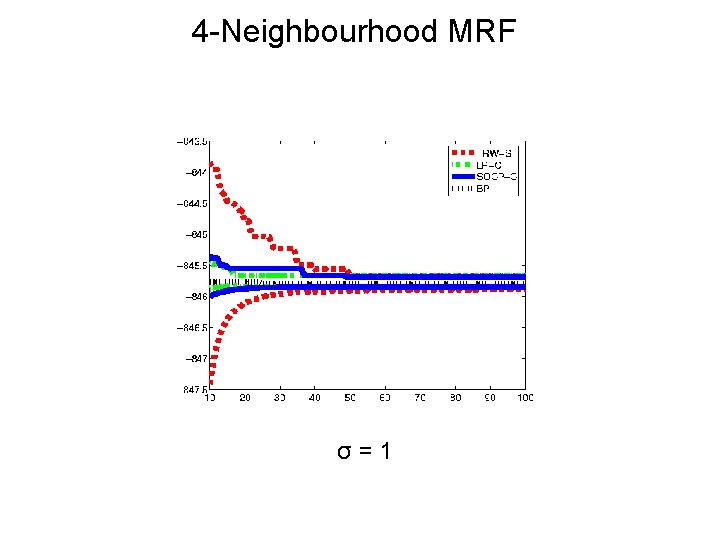
4 -Neighbourhood MRF σ=1

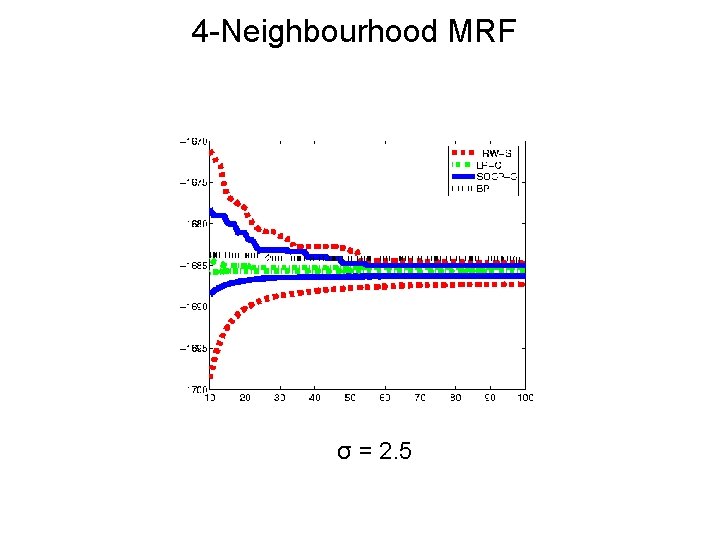
4 -Neighbourhood MRF σ = 2. 5

8 -Neighbourhood MRF σ = 1/ 2

8 -Neighbourhood MRF σ = 2. 5 / 2