ECMWF Data Assimilation Training Course Kalman Filter Techniques

ECMWF Data Assimilation Training Course Kalman Filter Techniques Mike Fisher Slide 1 ECMWF

Kalman Filter – Derivation 1 l Consider a general linear analysis: l Define errors, l Then: - Where is representativeness error. l Assume that the errors are unbiased. Slide 2 ECMWF

Kalman Filter – Derivation 1 l Assume that is uncorrelated with l The covariance matrix for the analysis error is: Slide 3 ECMWF

Kalman Filter – Derivation 1 l Use the following matrix calculus identities: l To get: Slide 4 ECMWF

Kalman Filter – Derivation 1 l Minimum variance => l I. e. l This is the Kalman gain matrix Slide 5 ECMWF

Kalman Filter – Derivation 1 l The Kalman filter consists of two sets of equations. l The first set define the minimum–variance, linear analysis, and its covariance matrix: - where: Slide 6 ECMWF

Kalman Filter – Derivation 1 l The second set of equations describe how to propagate the state and the covariance matrix so that they can be used for the background for the next cycle of analysis. l For the state, we have: - where is a linear model. l The equation for the error is: - where is the model error. Slide 7 ECMWF

Kalman Filter – Derivation 1 l Assume that model error is unbiased, and uncorrelated with analysis error, and form the covariance matrix: l I. e. Slide 8 ECMWF

Kalman Filter – Derivation 1 l The Kalman Filter Equations: Slide 9 ECMWF

Extended Kalman Filter (EKF) l The Extended Kalman Filter is an ad hoc generalization of the Kalman filter to weakly non-linear systems. l The forecast model and observation operators are allowed to be non-linear: l The matrices and in the equations for and are the linearized about and. l NB: The EKF requires tangent linear and adjoint codes! l The Iterated Extended Kalman Filter (IEKF) repeats the linearization of Hk as soon as a better estimate for the state is available – much like incremental 4 d. Var. Slide 10 ECMWF

Kalman Filter for Large Dimensions l The Kalman filter is impractical for large dimension systems. l It requires us to handle matrices of dimension N×N, where N is the dimension of the state vector. l This is out of the question if N~106. l Propagating the covariance matrix using: requires N integrations of the tangent linear model. l Even the matrix multiplies required to construct prohibitively expensive. are l A range of reduced-rank, approximate Kalman filters have been developed for use in large systems. Slide 11 ECMWF

Reduced-Rank Methods l Reduced-rank methods approximate the Kalman filter by restricting the covariance equations to a small subspace. l Suppose we can write with K small (e. g. K~100). , where is N×K, l The Kalman gain becomes : l The initial in this equation means that the analysis error covariance is also restricted to the subspace: Slide 12 ECMWF

Reduced-Rank Methods l Hence, the covariance may be propagated using only K integrations of the linear model: l We can then project onto a new subspace to generate an approximate covariance matrix for use in the next analysis cycle. Slide 13 ECMWF

Reduced-Rank Methods l It is important to remember that reduced-rank Kalman filters are approximations to the full Kalman filter. l They are not optimal. l How sub-optimal are they, e. g. compared to 4 d. Var? - The jury is still out! l A particular defect is the leading in: l This means that the analysis increment is restricted to lie in the space spanned by the columns of. l This is sometimes called the “rank problem”. Slide 14 ECMWF

Ways Around the Rank Problem l We can allow increments in directions orthogonal to the columns of by using a sub-optimal gain matrix, in the directions orthogonal to the columns of. - where Π represents projection onto the columns of . l NB: What is meant by “projection” must be carefully defined, especially in a multi-variate system. - The choice of inner product is rarely discussed! Slide 15 ECMWF

Ways Around the Rank Problem l Another consequence of approximating by a low-rank matrix is that spurious long-range correlations are produced. l Example: - Suppose there is a spurious long-range correlation between Antarctica and Europe. - The analysis will find it difficult to generate increments over Antarctica, since these will contradict the observations over Europe. l More generally, the analysis will not have enough available degrees of freedom to allow it to fit all the observations (100 degrees of freedom v. 105 obs!). l Two ways around this problem are: - local analysis (e. g. Evensen, 2003, Ocean Dynamics pp 343 -367) - Schur product (e. g. Houtekamer and Mitchell, 2001, MWR pp 123 -137) Slide 16 ECMWF

Ways Around the Rank Problem l Local analysis applies the analysis equation independently to each gridpoint (or to a each of a set of regions). l Each analysis uses only observations that are local to the gridpoint (or region). l In this way, the analysis at each gridpoint (or region) is not influenced by distant observations. l The global analysis is no longer a linear combination of the spanning vectors. l The method acts to vastly increase the effective rank of the covariance matrix. l The analysis is sub-optimal because, at each gridpoint, only a subset of available information is used. Slide 17 ECMWF

Ways Around the Rank Problem l The Schur product of two matrices, denoted is the element-wise product: . , l Spurious, long-range correlations may be removed from by forming the Schur product of the covariance matrix with a matrix representing a decaying function of distance. l The modified covariance matrix is never explicitly formed (it is too big). Rather, the method deals with terms such as. l The Schur product has the effect of vastly increasing the effective rank of the covariance matrix. l Choosing the product function is non-trivial. It is easy to modify the correlations in undesirable ways. E. g. balance relationships may be adversely affected. Slide 18 ECMWF

Ensemble Methods l Ensemble Kalman filters are reduced-rank Kalman filters that construct their covariance matrices as sample covariance matrices: - where the index, i, refers to sample (ensemble) member. - is a sample (ensemble) of analysis states whose sample covariance matrix is an estimate of the true analysis error covariance matrix. l Given a sample of analysis states, , a sample of background states for the next analysis cycle is produced by: - where - NB: The full nonlinear model is used to propagate the states. is a noise process with covariance matrix Qk+1. Slide 19 ECMWF

Ensemble Methods l The terms involving in the analysis equation are also represented as sample error covariance matrices: l It is never necessary to explicitly form the N×N background error covariance matrix. l No tangent linear or adjoint observation operators or models are required. Slide 20 ECMWF

Ensemble Methods l The random sample , may be generated by perturbing the observations with random noise drawn from the covariance matrix of observation error (Burgers et al. , 1998, MWR pp 1719 -1724). l This method is similar to the analysis-ensemble method for generating Jb statistics. l Adding noise to the observations results in additional sampling noise. l This additional noise is avoided in the Ensemble Adjustment Kalman Filter (EAKF, Anderson 2001, MWR 2884 -2903) and the Ensemble Transform Kalman Filter (ETKF, Bishop et al. 2001, MWR 420 -436). Slide 21 ECMWF

Ensemble Methods l The ensemble adjustment Kalman filter avoids the need to add noise by implicitly calculating a matrix A, such that: - and l The ensemble transform Kalman filter calculates T such that Va represents an analysis sample in: l These methods can be more accurate than the perturbedobservation method, but they make heavier demands on the linearity of the underlying system, and on the Gaussian assumption for the statistics. Slide 22 ECMWF

Other Low-Rank Methods l Ensemble methods are popular and attractive because they don’t require adjoint or tangent linear codes. However, a random basis is unlikely to be optimal. l Singular vectors, bred modes, etc. can be used to define deterministic subspaces for reduced-rank Kalman filtering that attempt to capture important aspects of covariance evolution. l ECMWF RRKF (R. I. P. ) - defined a subspace that evolved into the leading eigenvectors of the forecast error covariance matrix at day 2. l SEEK, SEIK, SEPLK (Pham et al, 1998) - a plethora of evolving/partially-evolving subspaces and a plague of acronyms! l Reduced Order Kalman Filter (Farrell and Ioannou, 2001) - uses model-reduction techniques to define an optimal subspace. Slide 23 ECMWF

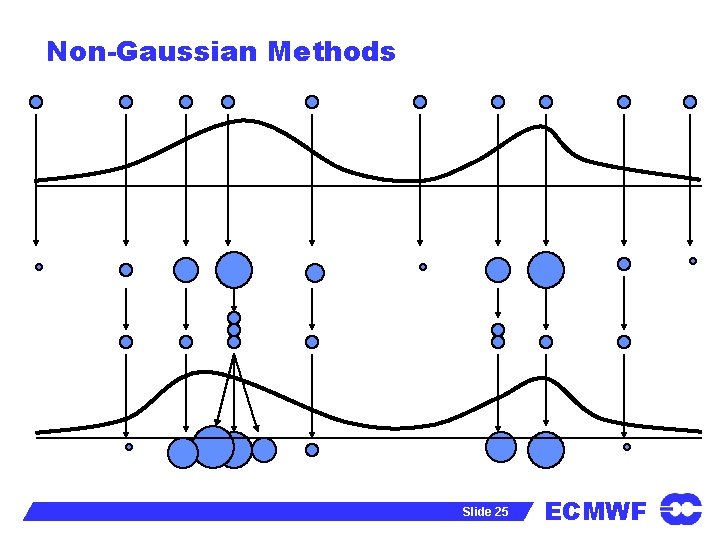
Non-Gaussian Methods l Particle filters approximate the forecast pdf by a discrete distribution: l An ensemble of forecasts, x(1). . . x(K) is run. Each member of the ensemble has an associated weight, w(i). l When an observation is available, the weights are adjusted using Bayes’ theorem. E. g: l Eventually, the weights for some members become tiny. l These members are dropped from the ensemble, and replaced by new, more probable members. Slide 24 ECMWF

Non-Gaussian Methods Slide 25 ECMWF

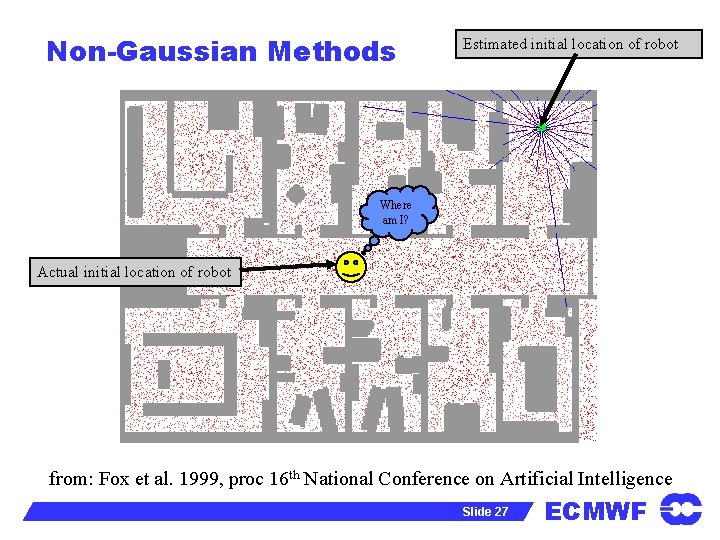
Non-Gaussian Methods l Particle filters work well for highly-nonlinear, lowdimensional systems. - Successful applications include missile tracking, computer vision, etc. (see the book “Sequential Monte Carlo Methods in Practice”, Doucet, de Freitas, Gordon (eds. ), 2001) l van Leeuwen (2003) has successfully applied the technique for an ocean model. l The main problem to be overcome is that, for a largedimensional system, with lots of observations, almost any forecast will contradict an observation somewhere on the globe. - => Every cycle, unless the ensemble is truly enormous, all the particles (forecasts) are highly unlikely (given the obseravtions). - van Leeuwen has recently suggested methods that may get around this problem. Slide 26 ECMWF

Non-Gaussian Methods Estimated initial location of robot Where am I? Actual initial location of robot from: Fox et al. 1999, proc 16 th National Conference on Artificial Intelligence Slide 27 ECMWF

Non-Gaussian Methods from: Fox et al. 1999, proc 16 th National Conference on Artificial Intelligence Slide 28 ECMWF

The Non-Sequential Approach l All the preceding is based on the sequential (recursive) view of the filtering problem: l An optimal estimate for step k+1 is produced using only the state and covariance matrices from step k. l All the information from earlier steps is brought to the present step via the covariance matrices. l The advantage of the sequential approach is that we don’t need to go back any further than the previous step in order to determine the current analysis. l The disadvantage is that we must explicitly propagate the covariance matrices. l For very large systems, the matrices are so enormous that a non-sequential approach may be preferable. Slide 29 ECMWF

Slide 30 ECMWF

Equivalence of Kalman Smoother and 4 d. Var l Suppose we want to produce the optimal estimate of the states x 0. . . x. K, at steps 0. . . K, given observations y 0. . . y. K at steps 0. . . K, and a background state xb at step 0. l Assuming errors are Gaussian, the probability of x 0. . . x. K given y 0. . . y. K and xb is: Slide 31 ECMWF

Equivalence of Kalman Smoother and 4 d. Var l Taking the logarithm gives us the weak-constraint 4 d. Var cost function: l The maximum likelihood solution is given by the minimum of the cost function. - For Gaussians, this is also the minimum-variance solution. l Hence, at step K, weak-constraint 4 d. Var gives the same (minimum-variance) solution as the Kalman filter. Slide 32 ECMWF

Equivalence of Kalman Smoother and 4 D-Var l The solution of the minimization problem differs from the Kalman filter solution at steps 0…K-1. - The 4 d. Var solution for step k is optimal with respect to observations at steps 0…K. - The Kalman filter solution at step k is optimal only with respect to observations at steps 0…k. l I. e. weak constraint 4 D-Var is equivalent to the Kalman smoother. - The lecture notes give a purely algebraic proof of this equivalence. - This proof shows that the equivalence does not depend on the statistical assumptions made in formulating the analysis problem. Slide 33 ECMWF

The Non-Sequential Approach l To determine the optimal state at step K, given observations at steps 0. . . K, and a background at step 0, we can: - Either: run a sequential Kalman filter, starting from the background at step 0, and updating the N×N covariance matrices at each step. - Or: minimize the weak-constraint 4 d. Var cost function using all observations for steps 0…K. l The sequential approach is impractical for large N. l In principle, the 4 d. Var approach becomes impractical as K becomes large. l What may save 4 d. Var is the limited memory of the Kalman filter. - The analysis is insensitive to observations in the distant past, because the Kalman filter can’t trust the imperfect model to propagate information over long periods of time. => We can minimize over steps K-p. . . K, instead of 0. . . K. Slide 34 ECMWF

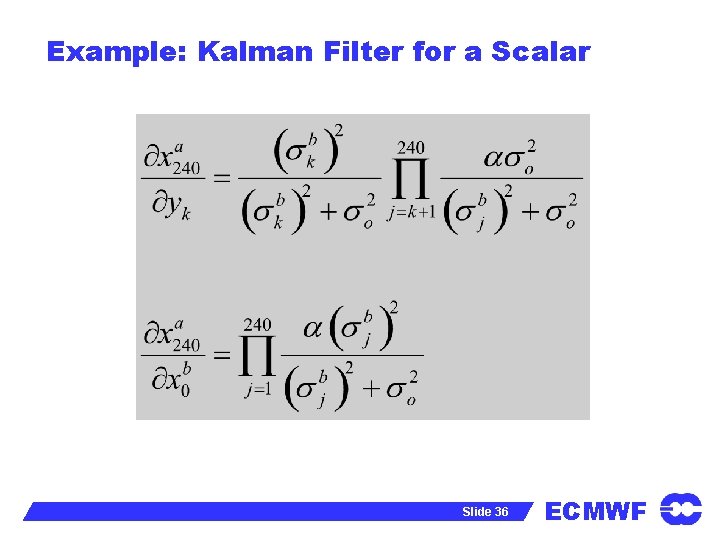
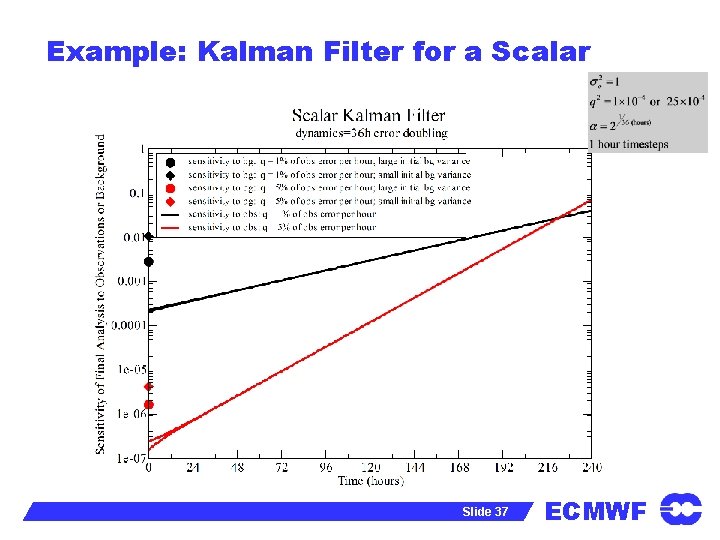
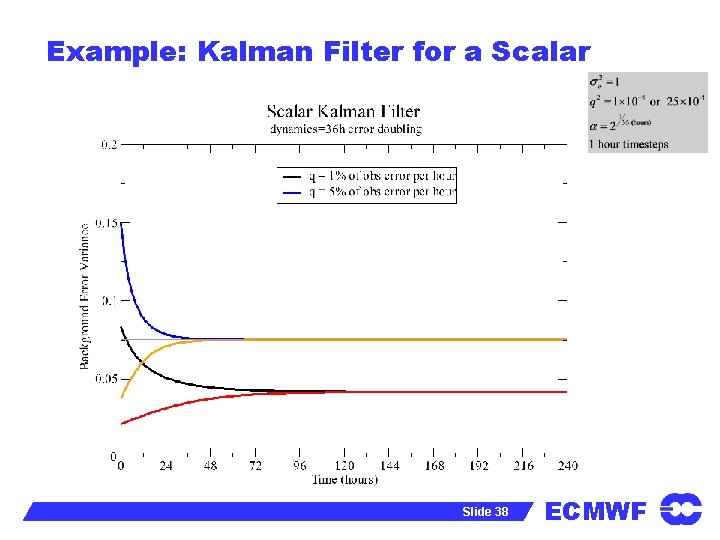
Example: Kalman Filter for a Scalar Analysis equation: Forecast equation: Analysis error variance: Variance evolution: Slide 35 ECMWF

Example: Kalman Filter for a Scalar Slide 36 ECMWF

Example: Kalman Filter for a Scalar Slide 37 ECMWF

Example: Kalman Filter for a Scalar Slide 38 ECMWF

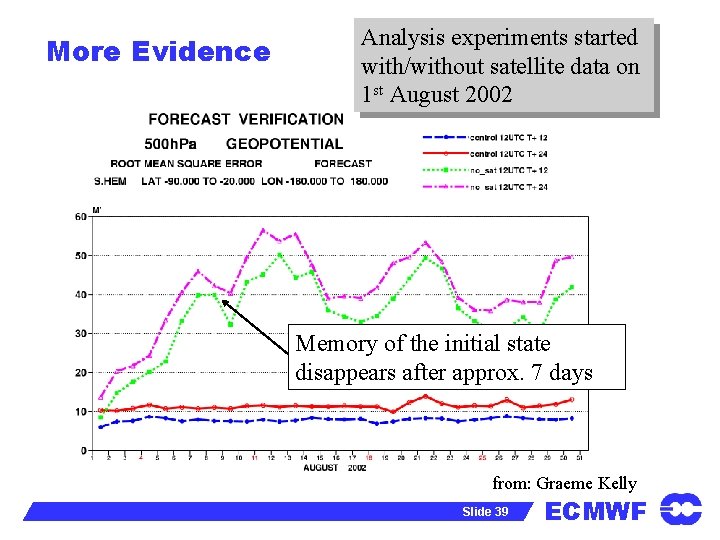
More Evidence Analysis experiments started with/without satellite data on 1 st August 2002 Memory of the initial state disappears after approx. 7 days from: Graeme Kelly Slide 39 ECMWF

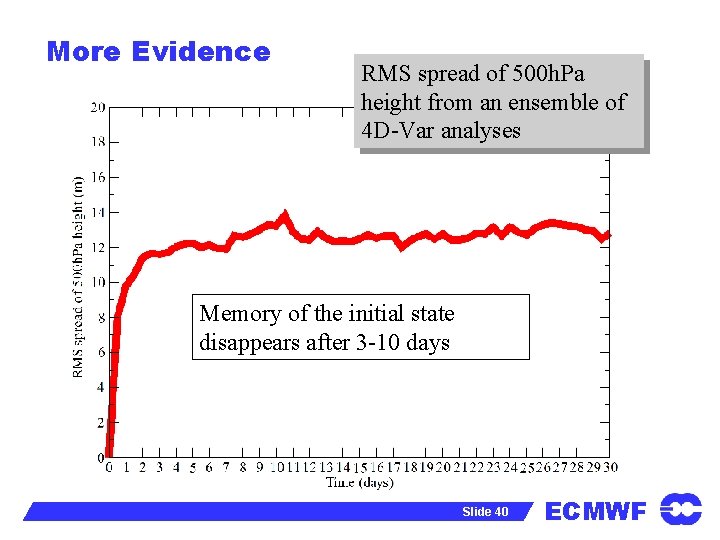
More Evidence RMS spread of 500 h. Pa height from an ensemble of 4 D-Var analyses Memory of the initial state disappears after 3 -10 days Slide 40 ECMWF

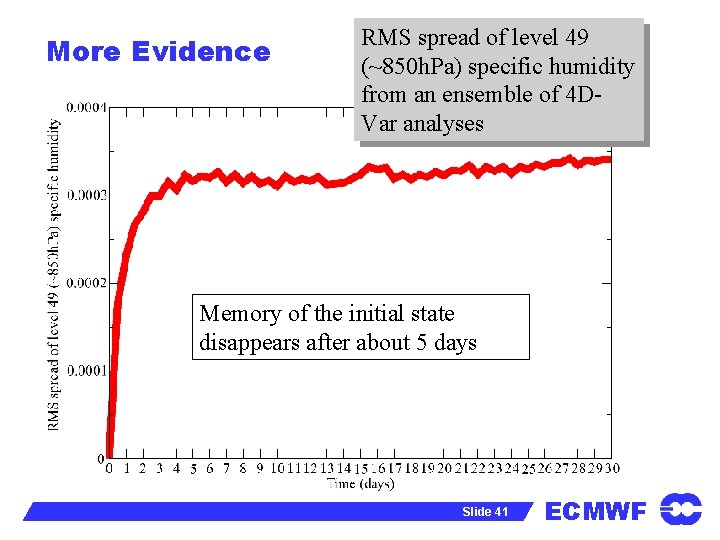
More Evidence RMS spread of level 49 (~850 h. Pa) specific humidity from an ensemble of 4 DVar analyses Memory of the initial state disappears after about 5 days Slide 41 ECMWF

Long-Window, Weak-Constraint 4 d. Var l Long window, weak constraint 4 d. Var is equivalent to the Kalman filter, provided we make the window long enough. l For NWP, 3 -10 days is long enough. l This makes long-window, weak constraint 4 d. Var expensive. l But, the resulting Kalman filter is full-rank. Slide 42 ECMWF

Summary l The Kalman filter is the optimal (minimum-variance) analysis for a linear system. l For weakly nonlinear systems, the extended Kalman filter can be used, but it needs adjoints and tangent linear models and observation operators. l Ensemble methods are relatively easy to develop (no adjoints required), but little rigorous investigation of how well they approximate a full-rank Kalman filter has been carried out. l Particle filters are interesting, but it is not clear how useful they are for large-dimension systems. l For large systems, the covariance matrices are too big to be handled. - We must either use low-rank approximations of the matrices (and risk destroying the advantages of the Kalman filter) - Or use the non-sequential approach (weak-constraint 4 d. Var). Slide 43 ECMWF