What is Data Assimilation Data Assimilation Data assimilation

What is Data Assimilation ? Data Assimilation: Data assimilation seeks to characterize the true state of an environmental system by combining information from measurements, models, and other sources. Typical measurements for hydrologic/earth science applications: • Ground-based hydrologic and geological measurements (stream flow, soil moisture, soil properties, canopy properties, etc. ) • Ground-based meteorological measurements (precipitation, air temperature, humidity, wind speed, etc. ) • Remotely-sensed measurements (usually electromagnetic) which are sensitive to hydrologically relevant variables (e. g. water vapor, soil moisture, etc. ) Mathematical models used for data assimilation: • Models of the physical system of interest. • Models of the measurement process. • Probabilistic descriptions of uncertain model inputs and measurement errors. A description based on combined information should be better than one obtained from either measurements or model alone.

Key Features of Environmental Data Assimilation Problems State estimation -- System is described in terms of state variables, which are characterized from available information Multiple data sources -- Estimates are often derived from different types of measurements (ground-based, remote sensing, etc. ) measured at different times and resolutions. State variables may fluctuate over a wide range of time and space scales -Different scales may interact (e. g. small scale variability can have large-scale consequences) Spatially distributed dynamic systems -- Systems are often modeled with partial differential equations, usually nonlinear. Uncertainty -- The models used in data assimilation applications are inevitably imperfect approximations to reality, model inputs may be uncertain, and measurement errors may be important. All of these sources of uncertainty need to be considered in the data assimilation process. The equations used to describe the system of interest are usually discretized over time and space -- Since discretization must capture a wide range of scales the resulting number of degrees of freedom (unknowns) can be very large.

State-Space Framework for Data Assimilation State-space concepts provide a convenient way to formulate data assimilation problems. Key idea is to describe system of interest in terms of following variables: • Input variables -- variables which account forcing from outside the system or system properties which do not depend on the system state. • State variables -- dependent variables of differential equations used to describe the physical system of interest, also called prognostic variables. • Output variables -- variables that are observed, depend on state and input variables, also called diagnostic variables. Classification of variables depends on system boundaries: Atmosphere Precip. ET Land System includes coupled land atmosphere -- precipitation and evapo-transpiration are state variables Atmosphere Precip. ET Land System includes only land, precipitation and evapotranspiration are input variables

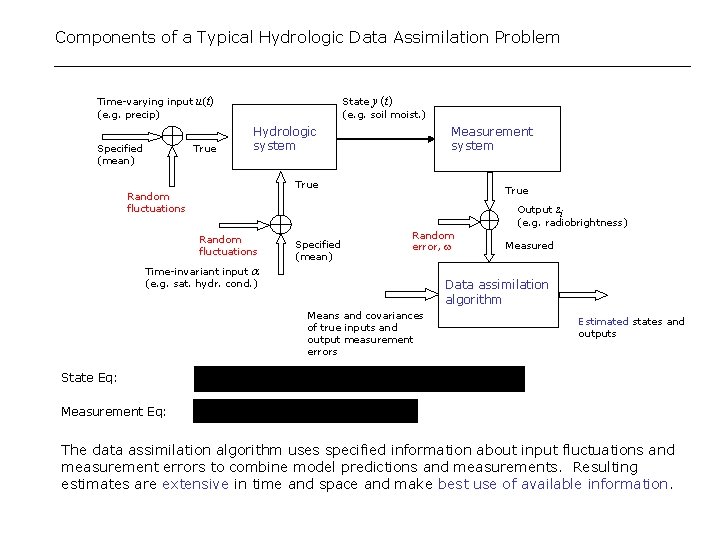
Components of a Typical Hydrologic Data Assimilation Problem Time-varying input u(t) (e. g. precip) Specified (mean) True State y (t) (e. g. soil moist. ) Hydrologic system Measurement system True Random fluctuations Output zi (e. g. radiobrightness) Random fluctuations Time-invariant input (e. g. sat. hydr. cond. ) Specified (mean) Random error, Measured Data assimilation algorithm Means and covariances of true inputs and output measurement errors Estimated states and outputs State Eq: Measurement Eq: The data assimilation algorithm uses specified information about input fluctuations and measurement errors to combine model predictions and measurements. Resulting estimates are extensive in time and space and make best use of available information.

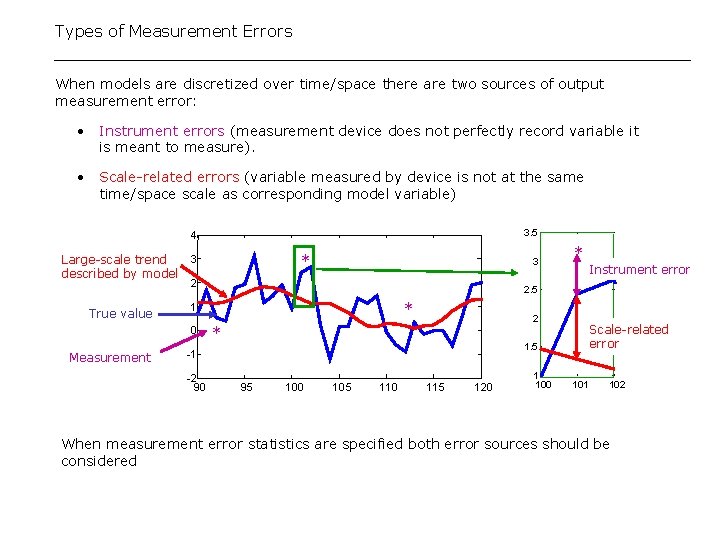
Types of Measurement Errors When models are discretized over time/space there are two sources of output measurement error: • Instrument errors (measurement device does not perfectly record variable it is meant to measure). • Scale-related errors (variable measured by device is not at the same time/space scale as corresponding model variable) 3. 5 4 Large-scale trend described by model True value 3 2 * Instrument error Scale-related error 1. 5 -1 -2 90 * 2. 5 1 0 Measurement * 3 95 100 105 110 115 120 1 100 101 102 When measurement error statistics are specified both error sources should be considered

Types of Data Assimilation Problems - Temporal Aspects Zi = [z 1, z 2, …, zi] =Set of all measurements through time ti Interpolation: no time-dependence, characterize system only at time t=t Use for interpolation of spatial data (e. g. kriging) i t=ti Smoothing: characterize system over time interval t t i Use for reanalysis of historic data t 1 t 2 t ti Filtering/forecasting: characterize system over time interval t t i Use for real-time forecasting t 1 t 2 ti t

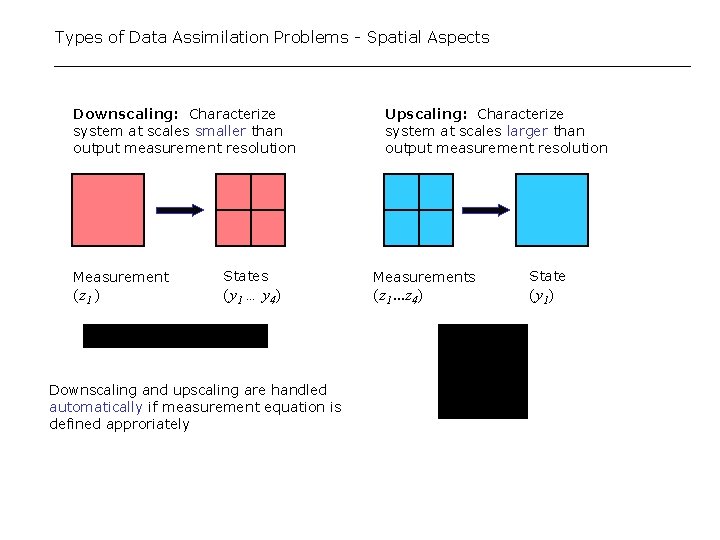
Types of Data Assimilation Problems - Spatial Aspects Downscaling: Characterize system at scales smaller than output measurement resolution Measurement (z 1 ) States (y 1 … y 4) Downscaling and upscaling are handled automatically if measurement equation is defined approriately Upscaling: Characterize system at scales larger than output measurement resolution Measurements (z 1. . . z 4) State (y 1)

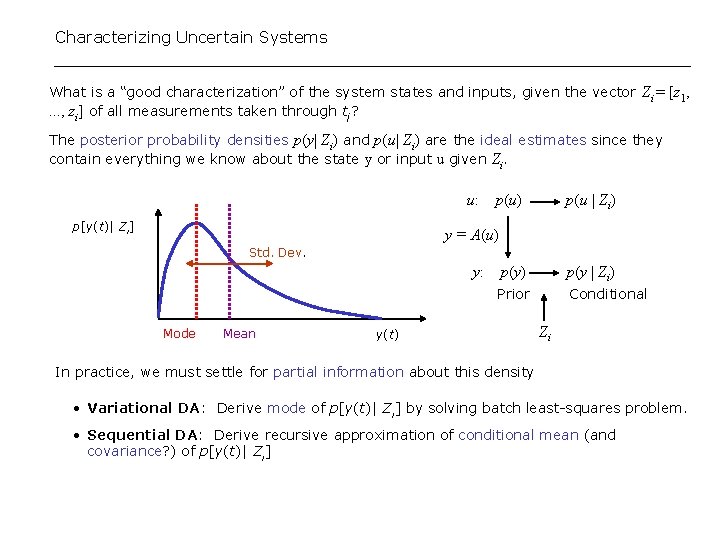
Characterizing Uncertain Systems What is a “good characterization” of the system states and inputs, given the vector Zi = [z 1, . . . , zi] of all measurements taken through ti? The posterior probability densities p(y| Zi) and p(u| Zi) are the ideal estimates since they contain everything we know about the state y or input u given Zi. u: p[y(t)| Zi] p(u) p(u | Zi) y = A(u) Std. Dev. y: Mode Mean p(y) p(y | Zi) Prior Conditional y(t) Zi In practice, we must settle for partial information about this density • Variational DA: Derive mode of p[y(t)| Zi] by solving batch least-squares problem. • Sequential DA: Derive recursive approximation of conditional mean (and covariance? ) of p[y(t)| Zi]

The Variational/Batch Approach Most variational methods use the mode of p u|z(u| Zi) as an estimate of uncertain input vector. State estimate is obtained by substituting into state equation: If and u are multivariate normal is the value of generalized least-squares error measure: that minimizes the following Terms that do not depend on The state equation is often incorporated as a constraint, using adjoint methods. u 2 is found with an iterative search. Search convergence is improved by the presence of the second (regularization) term in JB. u 1

The Sequential Approach Sequential methods are designed to propagate and update the conditional pdf in a series of discrete steps: Meas. 1 z 1 Meas. 2 z 2 Z 1 = [z 1 ] t 0 t 1 p y 1 [ y 1 ] Propagation 0 to 1 p y 0 [ y 0] p y 1| z 1[ y 1|Z 1 ] Algorithm Update 1 initialized with unconditional (prior) PDF at t 0 Meas. zi Zi = [Zi-1 , zi ] Z 2 = [Z 1 , z 2 ] t 2 p y 2| z 1[ y 2|Z 1 ] Propagation 1 to 2 i ti p yi| zi-1[ yi|Zi-1 ] p yi| zi[ yi|Zi ] Update In practice various approximations must be introduced. i ti+1 p y, i+1| zi[ yi+1|Zi ] Propagation i to i+1

Some Common Sequential Data Assimilation Methods A common approximation is to assume that the conditional PDF is multivariate Gaussian. The update for conditional mean has the form: K weights measurements Propagated estimate update vs. model predictions Some common approximations: Direct insertion Update forced to equal measurements where available, interpolated from meas. elsewhere Nudging: K = empirically selected constant Optimal Interpolation: K derived from assumed (static) covariance Extended Kalman filter: K derived from covariances propagated with a linearized model, input fluctuations and measurement errors must be additive. Ensemble Kalman filter: K derived from a ensemble of random replicates propagated with a nonlinear model, form of input fluctuations and measurement errors is unrestricted.

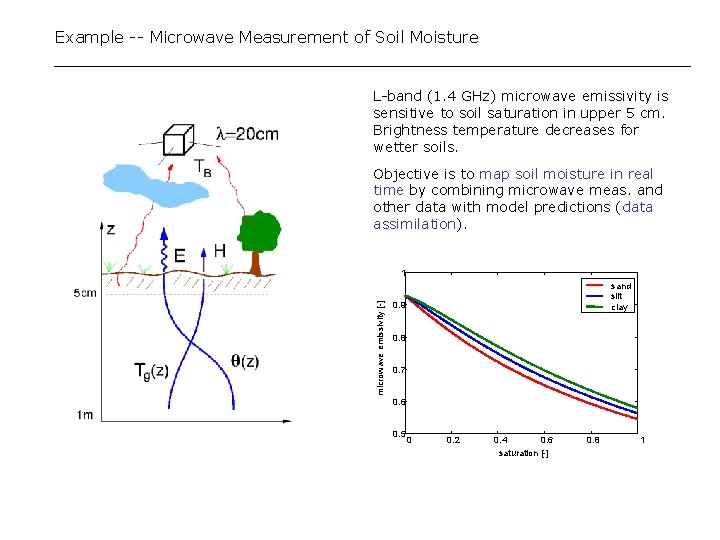
Example -- Microwave Measurement of Soil Moisture L-band (1. 4 GHz) microwave emissivity is sensitive to soil saturation in upper 5 cm. Brightness temperature decreases for wetter soils. Objective is to map soil moisture in real time by combining microwave meas. and other data with model predictions (data assimilation). microwave emissivity [-] 1 sand silt clay 0. 9 0. 8 0. 7 0. 6 0. 5 0 0. 2 0. 4 0. 6 saturation [-] 0. 8 1

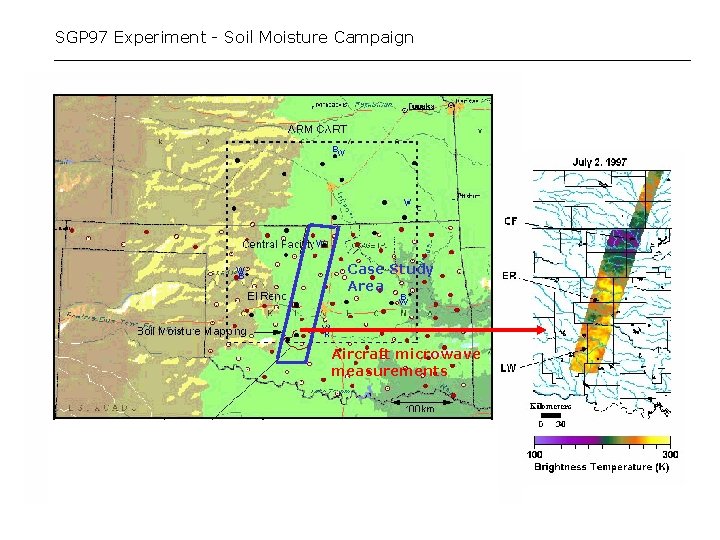
SGP 97 Experiment - Soil Moisture Campaign Case Study Area Aircraft microwave measurements

Problem Specifications –SGP 97 Ensemble Kalman Filter Example • Hydrologic model: 1 D (vertical) NOAH Land Surface Model (NOAA NCEP, Chen et al, 1996) applied at each estimation pixel • Radiative Transfer Model: Jackson et al , 1999 model applied at each pixel • Uncertain model inputs included in ensemble filter: Time-varying inputs: Precipitation (temporally uncorrelated) Time-invariant inputs: Porosity (upper bound on moisture content) Random fluctuations are multiplicative and lognormal (mean=1. 0) Wilting point (lower bound on moisture content) Saturated hydraulic conductivity Minimum stomatal resistance • Random measurement errors included in ensemble filter: Additive radiobrightness measurement noise • Filter assumes that random fluctuations and measurement errors for different pixels are uncorrelated

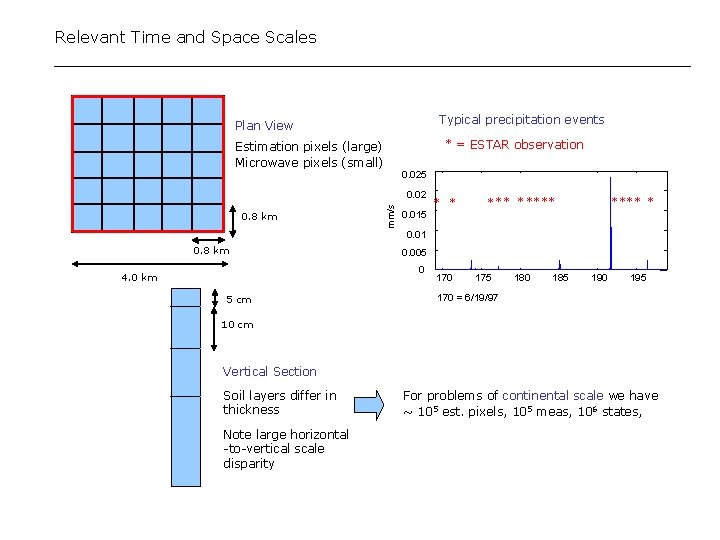
Relevant Time and Space Scales Typical precipitation events Plan View * = ESTAR observation Estimation pixels (large) Microwave pixels (small) 0. 025 0. 8 km mm/s 0. 02 0. 015 * ** * * 0. 01 0. 8 km 0. 005 0 4. 0 km 5 cm 170 175 180 185 190 195 170 = 6/19/97 10 cm Vertical Section Soil layers differ in thickness Note large horizontal -to-vertical scale disparity For problems of continental scale we have ~ 105 est. pixels, 105 meas, 106 states,

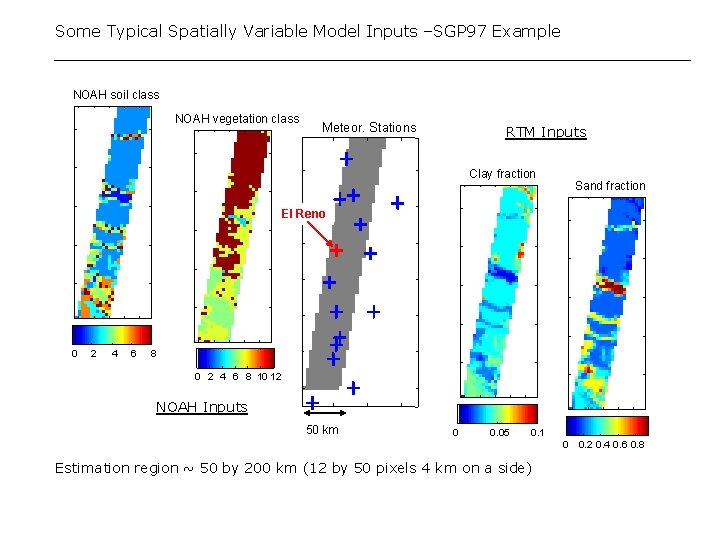
Some Typical Spatially Variable Model Inputs –SGP 97 Example NOAH soil class NOAH vegetation class Meteor. Stations RTM Inputs Clay fraction Sand fraction El Reno 0 2 4 6 8 10 12 NOAH Inputs 50 km 0 0. 05 0. 1 0 0. 2 0. 4 0. 6 0. 8 Estimation region ~ 50 by 200 km (12 by 50 pixels 4 km on a side)

Brightness Temperatures at a Typical Pixel – SGP 97 Example Precip Brightness temp. deg. K. Brightness Temp. and Precip Time Series – El Reno Brightness meas. Individual replicates Conditional mean Unconditional mean

Moisture Contents at a Typical Pixel – SGP 97 Example Precip Moisture content Moisture Content and Precip. Time Series – El Reno Brightness meas. times Individual replicates Conditional mean Unconditional mean Local spatial average of gravitimetric meas.

Comparison of Some Data Assimilation Options Variational methods • • Well-suited for smoothing problems, less convenient for real-time applications +/Does not provide information on estimation accuracy Difficult to accommodate time-dependent model errors, not robust – Most efficient forms require derivation of an adjoint model - Direct insertion, nudging, optimal interpolation • • Easy to implement + Updates do not account for system dynamics or input and measurement statistics No information on estimation accuracy – Computationally efficient + – Extended Kalman filter • • Can be adapted for real time or smoothing problems + Provides info. on estimation accuracy + Computationally demanding, limited capability to deal with model errors Linearization approximation may be poor, tends to be unstable - - Ensemble Kalman filter • • Well-suited for real time applications, not optimal for smoothing problems +/Provides information on estimation accuracy + Very flexible, modular, able to accommodate wide range of model error descriptions + No need for adjoint model or for linearizations or other approximations during propagation step Approach is robust and easy to use + Update assumes states are jointly normal – Can be computationally demanding – +