Data Structures www cp eng chula ac thvishnu

Data Structures www. cp. eng. chula. ac. th/~vishnu Vishnu Kotrajaras, Ph. D. 1

Introduction n Why study data structure? u. Can understand code written by others. u. Can choose a correct data structure for any task. Vishnu Kotrajaras, Ph. D. 2

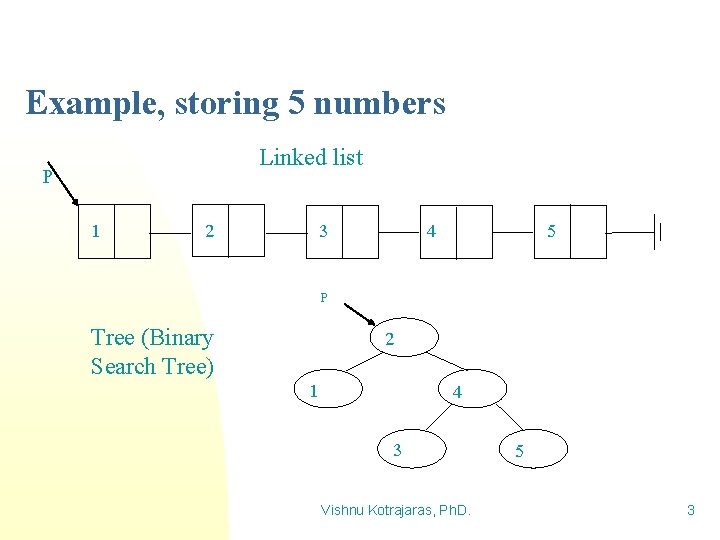
Example, storing 5 numbers Linked list P 1 2 3 4 5 P Tree (Binary Search Tree) 2 1 4 3 Vishnu Kotrajaras, Ph. D. 5 3

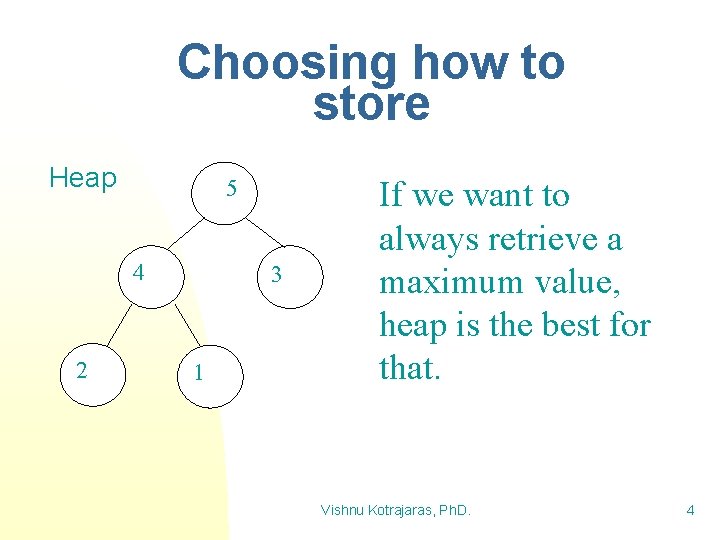
Choosing how to store Heap 5 4 2 3 1 If we want to always retrieve a maximum value, heap is the best for that. Vishnu Kotrajaras, Ph. D. 4

Estimating the program speed Big O if n where c and N 0 are constants and N>=N 0 n >see asymtotic. pdf page 2< n This is telling us how the program grows. n Vishnu Kotrajaras, Ph. D. 5

Find the speed of the following code sigma. Of. Square(int n) // calculate { 1 unit (declare only) 1: int temp. Sum; 1 unit (assignment) 2: temp. Sum = 0; n+1 unit n unit 3: for (int i=1; i<=n; i++) 1 unit Multiply, add, and 4: temp. Sum += i*i; assignment, each 5: return temp. Sum; has n times. } Total time is. 5 n+5 unit Therefore we have 1 unit (return) 3 n unit. Vishnu Kotrajaras, Ph. D. 6

We want to have a simple picture n n n It’s better to use an approximation time. That is Big O From the example, the time of the loop is dominant (other running times become insignificant) The loop is performed n times. u Therefore, Big O = O(n) n The detailed time is 5 n+5, which matches O(n) -> (5 n+5<= 6 n. ( Vishnu Kotrajaras, Ph. D. 7

Finding BIG O from various loops For loop-> Its Big O is the number of repetition. n Nested loop n times n 1: for (i = 1; i <= n; i++) n times 2: for (j = 1; j <= n; j++) statements; Big O is O(n 2). Vishnu Kotrajaras, Ph. D. 8

Finding BIG O from various loops(cont 2(. n Consecutive Statements 1: for (i = 0; i <= n; i++) O(n) 2: statement 1; 3: for (j = 0; j <= n; j++) 4: for (k = 0; k <= n; k++) 5: statement 2; O(n 2) The answer is their max. -> O(n 2) Vishnu Kotrajaras, Ph. D. 9

Finding BIG O from various loops(cont 3(. n Big O definition for consecutive statements: u. If T 1(N)=O(f(N)) and T 2(N)= O(g(N)), then «T 1(N)+ T 2(N)= max(O(f(N), O(g(N))) «From last page -> f(n) = O(n), g(n) = O(n 2) «The answer is therefore O(n 2) Vishnu Kotrajaras, Ph. D. 10

Finding BIG O from various loops(cont 4(. n Conditional statement 1: if (condition) 2: Statement 1 O(f(n)) 3: Else 4: Statement 2 O(g(n)) Use the max -> max(O(f(n), O(g(n))) Vishnu Kotrajaras, Ph. D. 11

Finding BIG O from recursion 1: mymethod (int n) { 2: if (n == 1) { 3: return 1; 4: } else { 5: return 2*mymethod(n – 1) + 1; 6: } 7: } n times, big O = O(n) Vishnu Kotrajaras, Ph. D. 12

Maximum Subsequence Sum Algorithm does matter n Maximum Subsequence Sum is: u For integer A 1, A 2, …, An u Maximum Subsequence Sum is that gives the maximum value. It is a consecutive sequence that gives the highest added value. u Example: 7 , 5 - , 16 , 6 - , 11 , 2 - consecutive « The sum of 11, -6, 16 is 21. But the max sequence is 11, -6, 16, -5, 7 -> the sum is 23. « 23 is the max. sub. Sum. Vishnu Kotrajaras, Ph. D. 13

Solving max sub sum: 1 st method 1: int max. Sub. Sum 01 ( int [] a) { 2: int max. Sum = 0; First index 3: for (int i = 0; i < a. length; i++) { Last index 4: for (int j = i; j < a. length; j++) { 5: int the. Sum = 0; 6: for (int k = i; k <= j; k++) { Sum from 7: the. Sum += a[k]; first to last. 8: } 9: if (the. Sum > max. Sum) {Choose 10: max. Sum = the. Sum; to store 11: } max 12: } value. 13: return max. Sum; 14: } Vishnu Kotrajaras, Ph. D. 14 15: }

Solving max sub sum: 1 st method(cont(. This first method has big O = O(n 3). n Not good enough. Too many redundant calculations. n u. If we have added elements from index 0 to 2, when we add elements from index 0 to 3, we should not start the addition from scratch. Vishnu Kotrajaras, Ph. D. 15

Solving max sub sum: 2 nd method 1: int max. Sub. Sum 02 (int [] a) { Starting 2: int max. Sum = 0; 3: for (int i = 0; i < a. length; i++) { position 4: int the. Sum = 0; 5: for (int j = i; j < a. length; j++) { Do the addition 6: the. Sum += a[j]; from the 7: if (the. Sum > max. Sum} ( starting : 8 max. Sum = the. Sum position { : 9 and collect { : 10 the result. BIG O = O(n 2) { : 11 : 12 return max. Sum; : 13 } Vishnu Kotrajaras, Ph. D. 16

Solving max sub sum: 2 nd method(cont(. -2 11 -6 4 when i=0, j=0: when i=0, j=1: when i=0, j=2: when i=0, j=3: the. Sum = -2 max. Sum = 0 the. Sum = -2 + 11 = 9 max. Sum becomes 9. max. Sum is still 9. the. Sum = 9 + (-6) = 3 the. Sum = 3 + 4 max. Sum is still 9. Vishnu Kotrajaras, Ph. D. 17

Solving max sub sum: 3 rd method Use divide and conquer n The result sequence maybe in u. The left half or the array, or u. The right half, or u. Lie between the left half and the right half. (its sequence contains the last element of the left half and the first element of the right half. ) n Vishnu Kotrajaras, Ph. D. 18

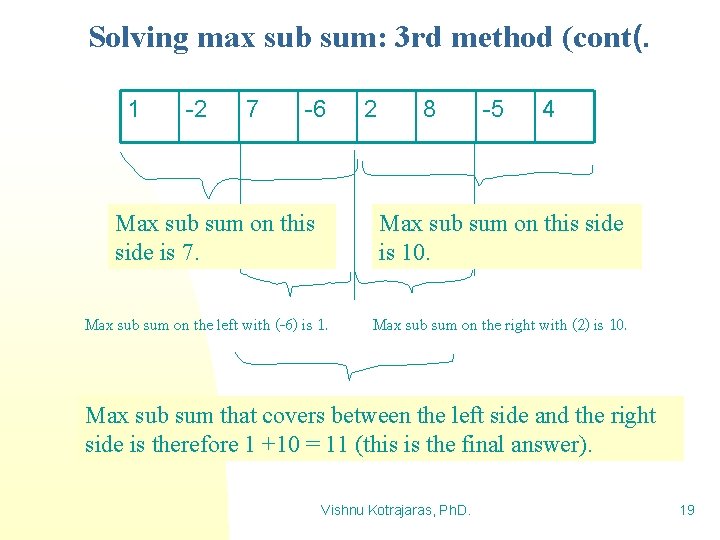
Solving max sub sum: 3 rd method (cont(. 1 -2 7 -6 Max sub sum on this side is 7. 2 8 -5 4 Max sub sum on this side is 10. Max sub sum on the left with (-6) is 1. Max sub sum on the right with (2) is 10. Max sub sum that covers between the left side and the right side is therefore 1 +10 = 11 (this is the final answer). Vishnu Kotrajaras, Ph. D. 19

Solving max sub sum: 3 rd method (cont 2(. 1: int max. Sum. Divide. Conquer (int [] array, int leftindex, int rightindex { 2: //assume that the array can be divided evenly. 3: if (leftindex == rightindex) { // Base Case T(n) 5: if (array[leftindex] > 0 ) 6: return array[leftindex]; 7: else 8: return 0; // min value of max. Sub. Sum T(n/2) 9: } 10: int centerindex = (leftindex + rightindex)/2; 12: int maxsumleft = max. Sum. Divide. Conquer(array, T(n/2) leftindex, centerindex); 13: int maxsumright = max. Sum. Divide. Conquer ( array, 20 centerindex + 1, right); Vishnu Kotrajaras, Ph. D.

Solving max sub sum: 3 rd method (cont 3(. 14: int maxlefthalf. Sum = 0, lefthalf. Sum = 0; 15: //max sum – from the last element of the left //side to the first element. 16: for (int i = center; i >= leftindex; i--) { 17: lefthalf. Sum = lefthalf. Sum + array[i]; 18: if (lefthalf. Sum > maxlefthalf. Sum) { 19: maxlefthalf. Sum = lefthalf. Sum; 20: } O(n/2) 21: } Vishnu Kotrajaras, Ph. D. 21

Solving max sub sum: 3 rd method (cont 4(. 22: int maxrighthalf. Sum = 0, righthalf. Sum = 0; 23: // max sum – from the first element of the right //side to the last element. 24: for (int i = centerindex + 1; i <= rightindex; i++) { 25: righthalf. Sum = righthalf. Sum + array [i]; 26: if (righthalf. Sum > maxrighthalf. Sum) { 27: maxrighthalf. Sum = righthalf. Sum; 28: } O(n/2) 29: } Vishnu Kotrajaras, Ph. D. 22

Solving max sub sum: 3 rd method (cont 5(. 30: //finally, find max of the three. 31: return max 3 (maxsumleft, maxsumright, maxlefthalf. Sum + maxrighthalf. Sum) } This part takes constant time. We can ignore. Therefore the total time is T(n) = 2 T(n/2) + 2 O(n/2) Using Master method we solve this equation u Big O = O(n log n) <skip to page 33< Vishnu Kotrajaras, Ph. D. 23

Solving max sub sum: 3 rd method (cont 6(. n We find the total BIG O: T(n) = 2 T(n/2) + 2 O(n/2) (2 T(n/2) + O(n = = 2 T(n/2) + cn O(n) <= c*n according to the definition Divide everything by n, we get: (1) Vishnu Kotrajaras, Ph. D. 24

Solving max sub sum: 3 rd method (cont 7(. n We can create a series of equations: (2) (3) (X) Vishnu Kotrajaras, Ph. D. 25

Solving max sub sum: 3 rd method (cont 8(. n Do (1) + (2) + (3) +…. . + (x), we get: u. The left and right hand side cancel each other out. And c is added for log 2 n times. u. Multiply both sides by n, we get: u. Because T(1) is constant, we can conclude that u. Big O = O(n log n( Vishnu Kotrajaras, Ph. D. 26

Solving max sub sum: 4 th method We improve on the 2 nd method, with two points to note: n First, the first element of any maximum subsequence sum cannot be a negative value. u. For example: 3, -5, 1, 4, 7, -4 n -5 cannot be the first element of our result. It can only make the total smaller. Any single positive number gives a better result anyway. Vishnu Kotrajaras, Ph. D. 27

Solving max sub sum: 4 th method (cont(. n Second, any subsequence that is negative cannot begin max sub sum. u. Let us be in a loop execution. Let i be the index of the first element of a subsequence an j be the index of the last element of that subsequence. u. Let the last element make this subsequence negative. u. Let p be any index between i+1 and j. 3 4 1 i -3 -9 p j 1 Vishnu Kotrajaras, Ph. D. 5 28

Solving max sub sum: 4 th method (cont 2(. « The next step of this loop -> increment j by one. • If a[j] is negative, we will not get a better max sub sum. Max sub sum value will not change. • If a[j] is positive, a[i]+…+a[j] will be greater than a[i]+…+a[j 1]. However, because a[i]+…+a[j-1] is negative, the new sum is never more than a stored max sub sum. The new sum cannot even match a[j] alone. • Therefore if we have a negative subsequence, we should not move j. We should move i instead. Vishnu Kotrajaras, Ph. D. 29

Solving max sub sum: 4 th method (cont 3(. «Should we only increment i by one or more? «From our assumption, we know that a[j] makes a[i]+…+a[j] negative. Therefore, incrementing i by one within the range between i and p will only make a[i]+…+ a[p] smaller. (p is any index between i and j). «If we want to get a larger max sub sum, we must start our subsequence from position j+1. Therefore i should be incremented to j+1. 3 4 1 i -3 -9 p j 1 Vishnu Kotrajaras, Ph. D. 5 30

Solving max sub sum: 4 th method (cont 4(. 1: int maxsubsum. Optimum (int[] array) { 2: int max. Sum = 0, the. Sum = 0; 3: for (int j = 0; j < a. length; j++) { 4: the. Sum = the. Sum + array [j]; 5: if ( the. Sum > max. Sum) { 6: max. Sum = the. Sum; 7: } else if (the. Sum < 0) { // if a[j] makes the 8: //sequence negative, 9: the. Sum = 0; // start again from 10: // position j+1. 11: } 12: } 13: return max. Sum; Vishnu Kotrajaras, Ph. D. 31 14: }

Logarithm in big O If we can spend a constant time (O(1)) to divide a problem into equal subproblems (3 rd method of the maximum subsequence sum problem), that problem will have big O = O(log n). n Usually , we make an assumption that all data is in the system. Otherwise, reading data in will take O(n). n Vishnu Kotrajaras, Ph. D. 32

Example: O)log n( n n n finding 5 in a sorted array. If we start from the first array member, it takes O(n) to find a number. But we know that the array is sorted: u So we can look at the middle of the array, and search from there, going to either left or right depending on the value of that middle element. u And keep searching by looking at the middle element of the subarray we are looking at, and so on. u This is called -> Binary Search. Vishnu Kotrajaras, Ph. D. 33

int binary. Search (int[] a, int x) { int left = 0, right = a. length – 1; while (left <=right) { int mid = (left + right)/2; if (a[mid] < x ) { left = mid + 1; Big O = O(log 2 n) } else if (a[mid] > x) { right = mid – 1; } else { return mid; } } return // ; 1 -reaching this point means -> not found. >goto page 39< Vishnu Kotrajaras, Ph. D. 34

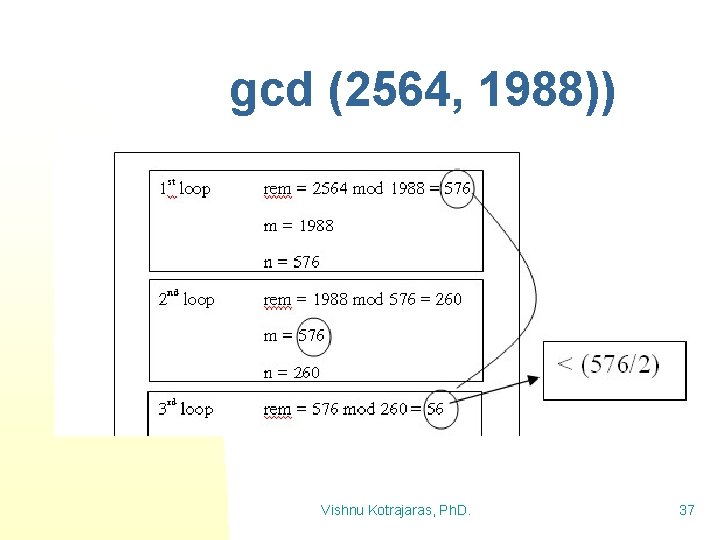
Example: O)log n) (cont(. n Greatest common divisor long gcd (long m , long n) { while (n!=0) { long rem = m%n; m = n; n = rem; } How do we find big O? return m; } The reduction of the remainder tells us the Big O. In this program, The remainder decreases without any specific pattern. Vishnu Kotrajaras, Ph. D. 35

Big O of gcd n n We use the following definition: if M > N, M mod N < M/2 u Prove: if N <= M/2: Because the remainder from M mod N must be less than N, so it must also be less than M/2. u if N > M/2: M divided by N will = 1 + (M-N). The remainder is M-N or M – (> M/2). Therefore the remainder is less than M/2. u n If we look at the code for gcd: The remainder from the xth loop will be used as m of the (x+2)th loop. u Therefore the remainder from the (x+2)th loop must be less than half the remainder from the xth loop. u Meaning -> with 2 iterations passed, the remainder must surely reduce by half or more. u Vishnu Kotrajaras, Ph. D. 36

gcd (2564, 1988)) Vishnu Kotrajaras, Ph. D. 37

Example: O)log n) (cont 2(. n Calculate xn by divide and conquer. long power (long x, int n) { Big O = O (log 2 n) if (n==0) The original problem is divided return 1; by half in each method call. if (is. Even (n)) return power (x*x, n/2); else return power (x*x, n/2)*x; } Vishnu Kotrajaras, Ph. D. 38

O(log n) definition logk n = O(n) when k is constant. u. This definition tells us that a logarithmic function has a small growth rate. n f(n) = loga n has its big O = O(logb n), where a and b is a positive number more than 1. u. Any two logarithmic functions have the same growth rate. n Vishnu Kotrajaras, Ph. D. 39

Any two logarithmic functions have the same growth rate: a proof n let and Vishnu Kotrajaras, Ph. D. 40

Runtime –small(top) to large (bottom) n n n n c log n logk n n n log n n 2 n 3 2 n Vishnu Kotrajaras, Ph. D. 41

Definitions other than big O Big Omega ( ) T(N) = (g(N)) if there exist constant C and N 0 that u. T(N) >= C g(N), where N>=N 0 n From def. if f(N) = (N 2), then f(N) = (N 1/2) u. We should choose the most realistic answer. n Vishnu Kotrajaras, Ph. D. 42

Definitions other than big O (CONT. ) Big Theta ( ) n T(N) = (h(N)) if T(N) = O(h(N)) and T(N) = (h(N)) n There exist c 1, c 2, N 0 that make c 1*h(N) <= T(N) <= c 2*h(N), where N >= N 0 n Vishnu Kotrajaras, Ph. D. 43

Definitions other than big O (CONT 2. ) small O n T(N) = o(p(N)) if T(N) = O(p(N)) but T(N) (p(N)) n Vishnu Kotrajaras, Ph. D. 44

Notes from the definitions n T(N) = O(f(N)) has the same meaning as f(N) = (T(N)) u We can say f(N) is an “upper bound” of T(N), and T(N) is a lower bound of f(N) = N 2 and g(N) = 2 N 2 have the same Big O ��� Big . That is f(N) = (g(N)) n f(N) = N 2 can have several Big O -> (O(N 3), O(N 4)) but the best value is O(N 2). n u We can use f(N) = (N 2) to tell that this value is the best big O. Vishnu Kotrajaras, Ph. D. 45

Thus, we have the latest definition: n n If T(N) is a Polynomial degree k, then T(N) = (Nk) From here, uif T(N) = 5 N 4 + 4 N 3 + N, we know that T(N) = (N 4) Vishnu Kotrajaras, Ph. D. 46

Best case, Worst case, Average case worst case = a maximum running time possible. n best case = a minimum running time possible. n average case? n u For each input, see how long the program runs. u average case running time = total time from every input divided by the number of input. Vishnu Kotrajaras, Ph. D. 47

Average case The average case definition is based on an assumption that: u. Each input has equal chance of occurrence. n If we do not want the assumption, u. We must take a probability of each input into account. n Average case = (prob. of inputi * unit time when use inputi ) n Vishnu Kotrajaras, Ph. D. 48

Example: Finding Average case Let’s say we want to find x in an array of size n. n Best case: find x in the first array slot. n Worst case: x is in the array’s last slot, or x is not in the array at all. n Average case: n u Assume each array slot has an equal chance of having x inside. u Therefore, a chance of x being in a slot is 1/n. Vishnu Kotrajaras, Ph. D. 49

Example: Finding Average case (cont(. Average Case running time = 1/n * (steps used when finding x in the first slot) + 1/n * (steps used when finding x in the second slot) + . . . + 1/n * (steps used when finding x in the last slot, or not finding x at all) n = (1 + 2 +… + n) / n = (n+1)/2 n = O(n) = big O of worst case n Vishnu Kotrajaras, Ph. D. 50