Chapter 8 Disjoint Sets and Dynamic Equivalence Equivalence

Chapter 8 Disjoint Sets and Dynamic Equivalence

Equivalence Relations An equivalence relation R has three properties: – reflexive: for any x, x. Rx is true – symmetric: for any x and y, x. Ry implies y. Rx – transitive: for any x, y, and z, x. Ry and y. Rz implies x. Rz Example equivalence relations? • • Born in the same year as Live on same island as In same department, where two people are related if they are in the same department – This relationship is an equivalence relation if someone was in only one department An example of a relation in which town a is related to town b if traveling from a to b by road is possible. – This relationship is an equivalence relation if the roads are two-way. Disjoint Sets 2

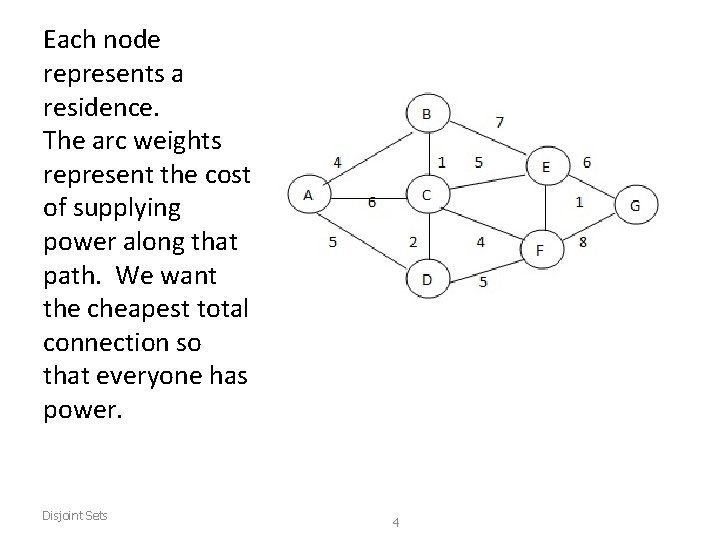
Example • Building electrical network for a new community. Want to make sure everybody has access to electricity with minimal cost. • Union – add wiring between two homes. • Find – Are you in same community as power supply? • This is called a spanning tree of a graph. Disjoint Sets 3

Each node represents a residence. The arc weights represent the cost of supplying power along that path. We want the cheapest total connection so that everyone has power. Disjoint Sets 4

Another example Disjoint Sets 5

Disjoint Set Union/Find ADT operations – union find(4) – find Name of 8 {1, 4, 8} – create – destroy {6} {7} {2, 3, 6} {5, 9, 10} union(2, 6) {2, 3} Disjoint set equivalence property: every element of a Disjoint set structure belongs to exactly one set Dynamic equivalence property: the sets can change after execution of a union Disjoint Sets 6

Disjoint Set Union/Find More Formally Given a set U = {a 1, a 2, … , an} • Maintain a partition of U, a set of subsets of U {S 1, S 2, … , Sk} such that: - each pair of subsets Si and Sj are disjoint: - together, the subsets cover U: • Union(a, b) creates a new subset which is the union of a’s subset and b’s subset NOTE: outside agent decides when/what to union – Abstract Data Type (ADT) is just the bookkeeper • Find(a) returns a unique name for a’s subset. We don’t care what name is used. NOTE: set names are arbitrary! We only care that: Find(a) == Find(b) a and b are in the same subset Disjoint Sets 7

How implement? Array? Union(1, 4) Union(2, 3) Other elements in own set. Group ID 0 1 2 3 4 5 6 7 8 9 10 11 Disjoint Sets 0 4 3 3 4 5 6 7 8 9 10 11 How long to find? How long to union? 8

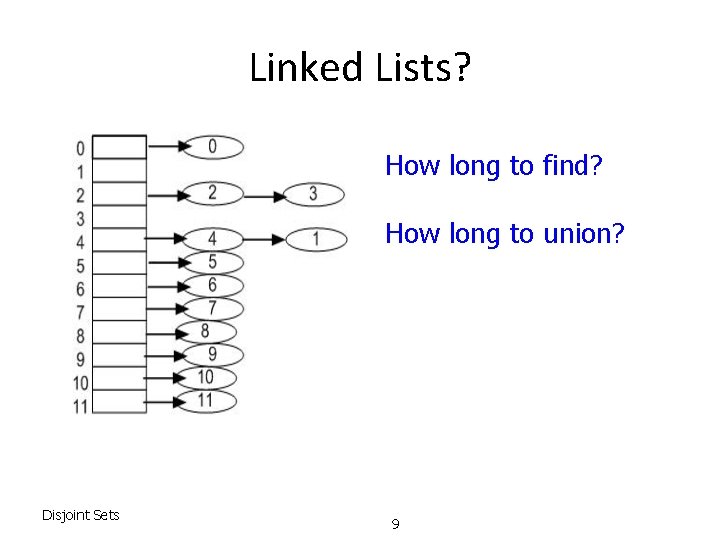
Linked Lists? How long to find? How long to union? Disjoint Sets 9

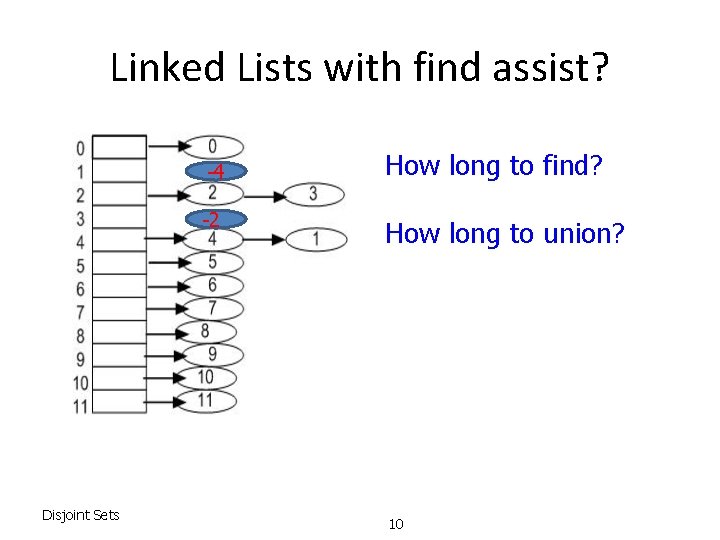
Linked Lists with find assist? -4 -2 Disjoint Sets How long to find? How long to union? 10

Up-Tree Intuition Finding the representative member of a set is somewhat like the inverse of finding whether a given item exists in a binary search tree. Instead of using trees with pointers from each node to its children; let’s use trees with a pointer from each node to its parent. Pay only for what you need: Note we never need to know the members of a set – just what set something is in. We have seen this idea of storing less information to facilitate fast operations. Where? If we don’t need as much functionality we may be able to create a special purpose data structure with good complexity. Since we are asking less functionality, we expect a better “cost”. 11

Question • With this representation, how would you do a union? • Could you find out who is in the set and point them all to the parent (directly)? • Would you want to do that? (The doorbell rings…) Disjoint Sets 12

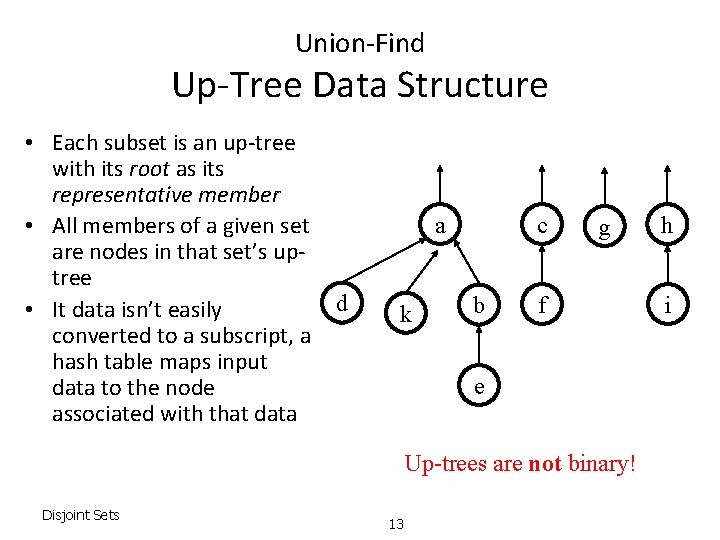
Union-Find Up-Tree Data Structure • Each subset is an up-tree with its root as its representative member • All members of a given set are nodes in that set’s uptree • It data isn’t easily converted to a subscript, a hash table maps input data to the node associated with that data a d k c b g f e Up-trees are not binary! Disjoint Sets 13 h i

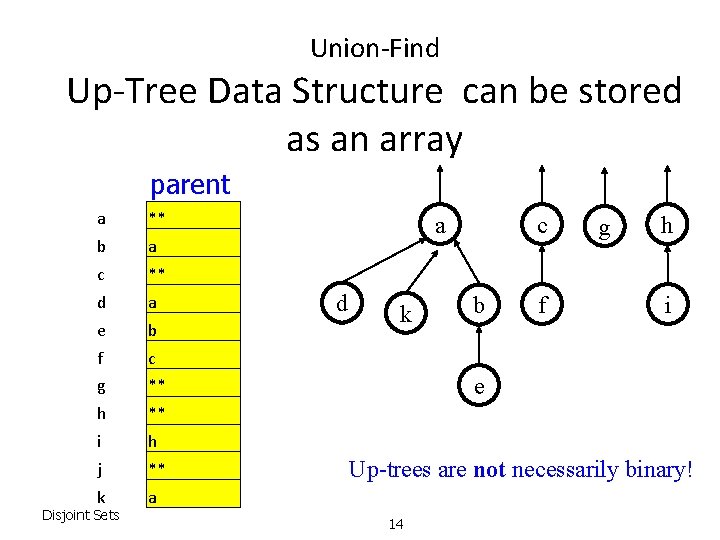
Union-Find Up-Tree Data Structure can be stored as an array parent a ** b a c ** d a e b f c g ** h ** i h j ** k a Disjoint Sets a d k c b f g h i e Up-trees are not necessarily binary! 14

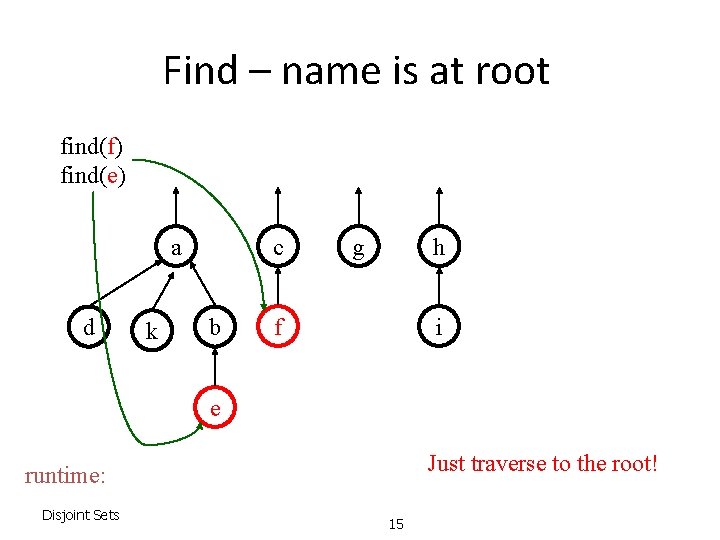
Find – name is at root find(f) find(e) a d k c b g h f i e Just traverse to the root! runtime: Disjoint Sets 15

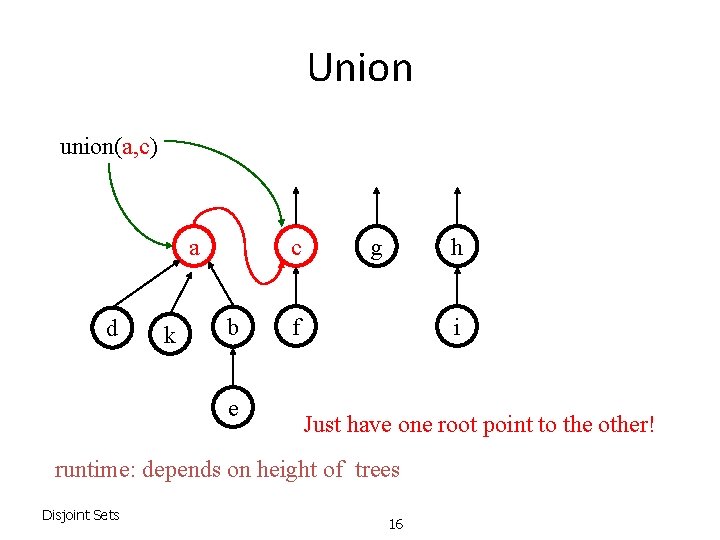
Union union(a, c) a d k c b e g h f i Just have one root point to the other! runtime: depends on height of trees Disjoint Sets 16

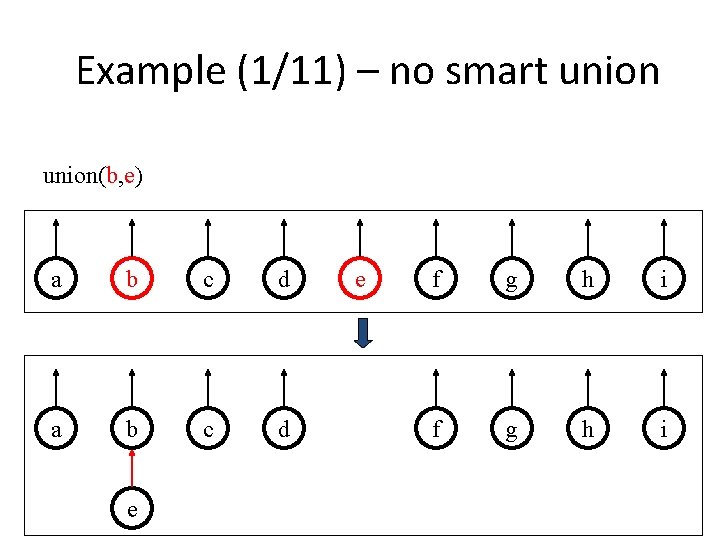
Example (1/11) – no smart union(b, e) a b c d e e f g h i

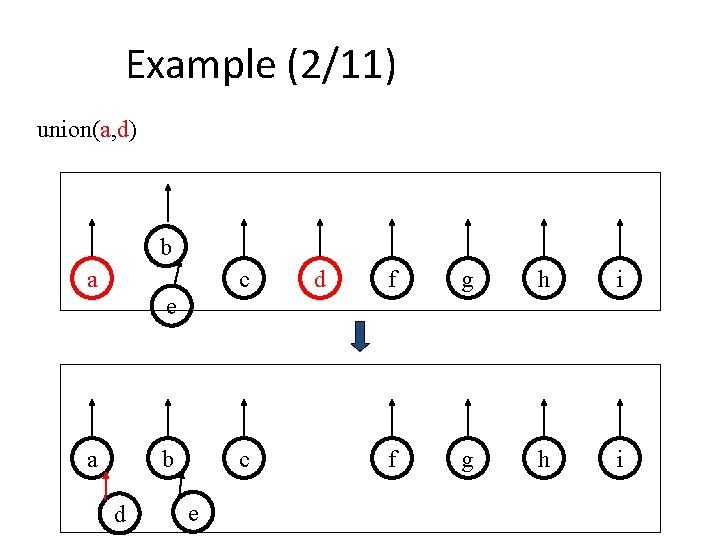
Example (2/11) union(a, d) b a c d f g h i e a b d c e

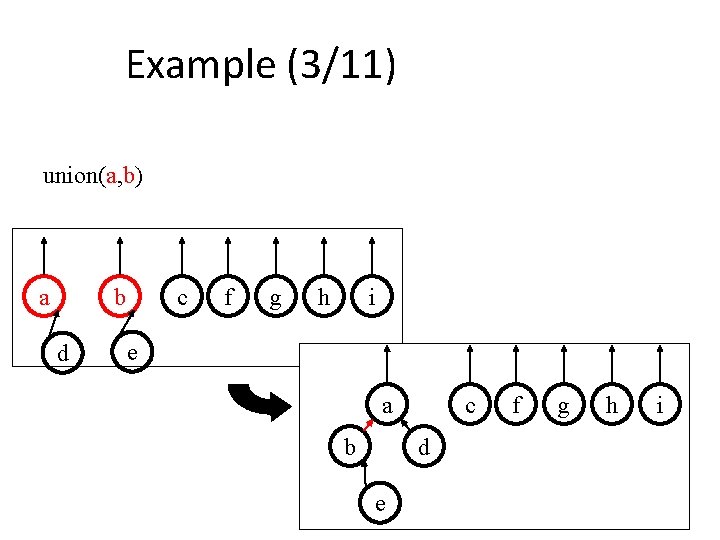
Example (3/11) union(a, b) a b d c f g h i e a b c d e f g h i

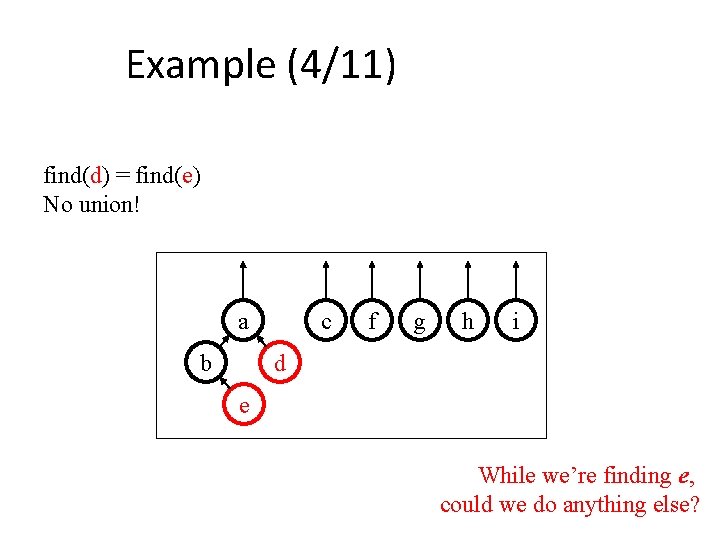
Example (4/11) find(d) = find(e) No union! a b c f g h i d e While we’re finding e, could we do anything else?

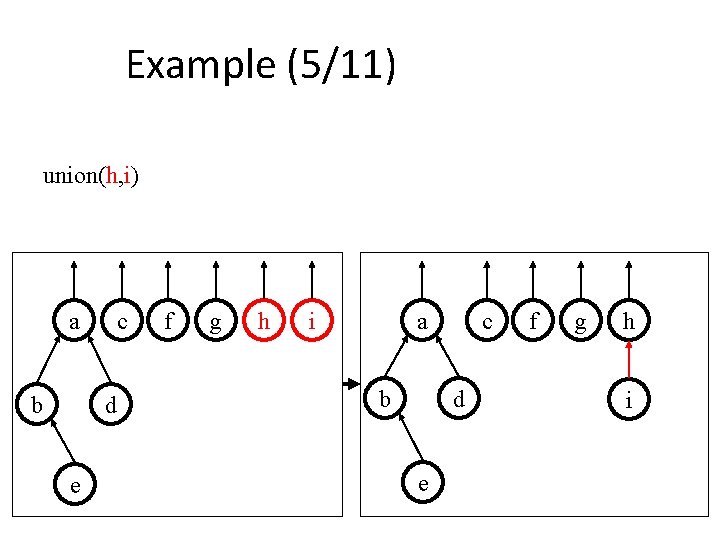
Example (5/11) union(h, i) a b c d e f g h i

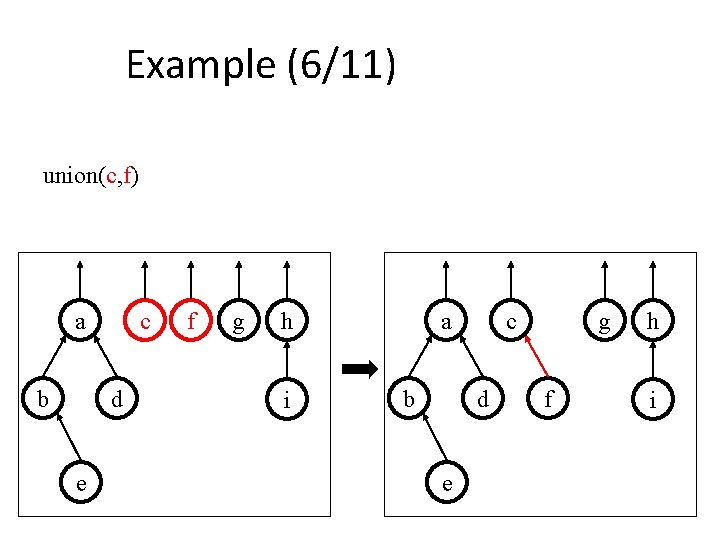
Example (6/11) union(c, f) a b c d e f g h i a b c d e g f h i

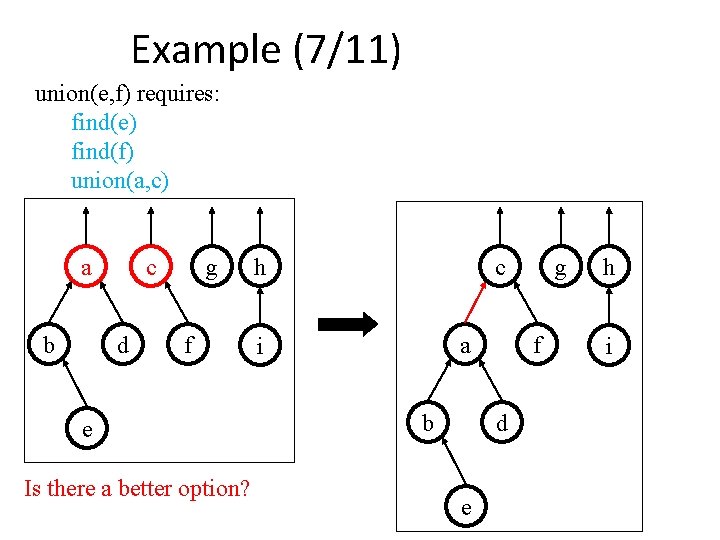
Example (7/11) union(e, f) requires: find(e) find(f) union(a, c) a b c d g f e Is there a better option? h c a i b f d e g h i

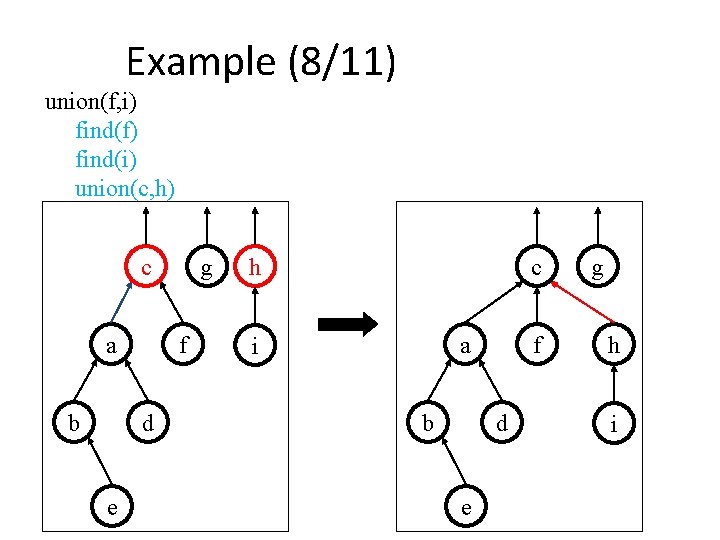
Example (8/11) union(f, i) find(f) find(i) union(c, h) c a b f d e g h c a i b f d e g h i

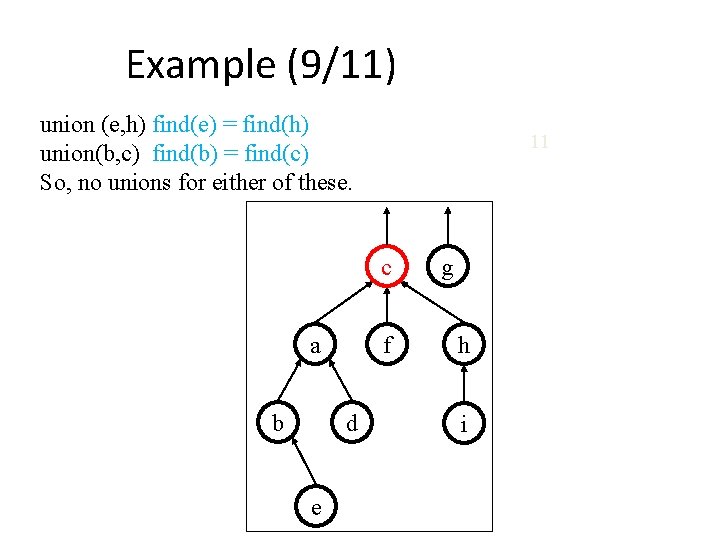
Example (9/11) union (e, h) find(e) = find(h) union(b, c) find(b) = find(c) So, no unions for either of these. 11 c a b f d e g h i

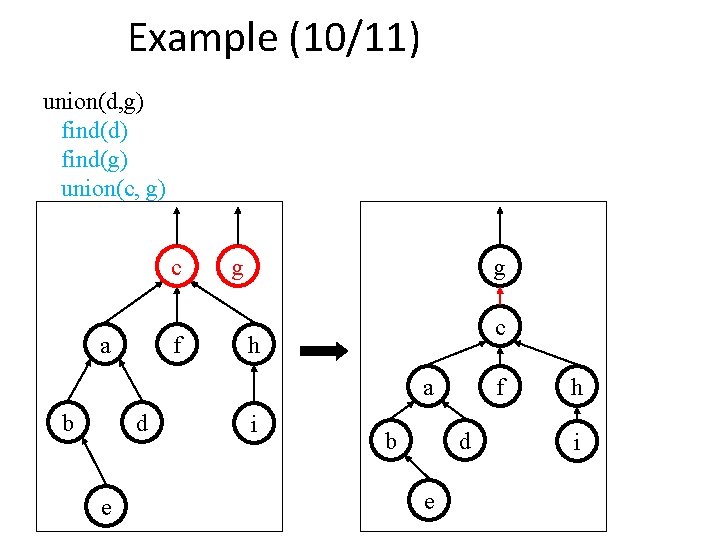
Example (10/11) union(d, g) find(d) find(g) union(c, g) c a f g g c h a b d e i b f d e h i

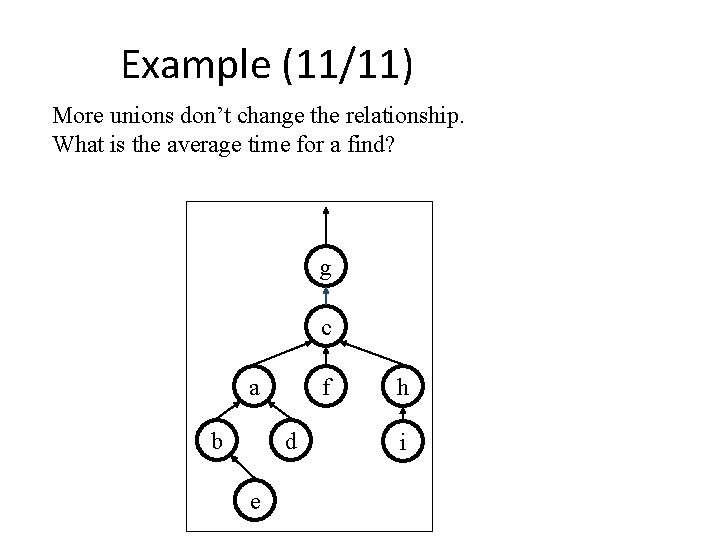
Example (11/11) More unions don’t change the relationship. What is the average time for a find? g c a b f d e h i

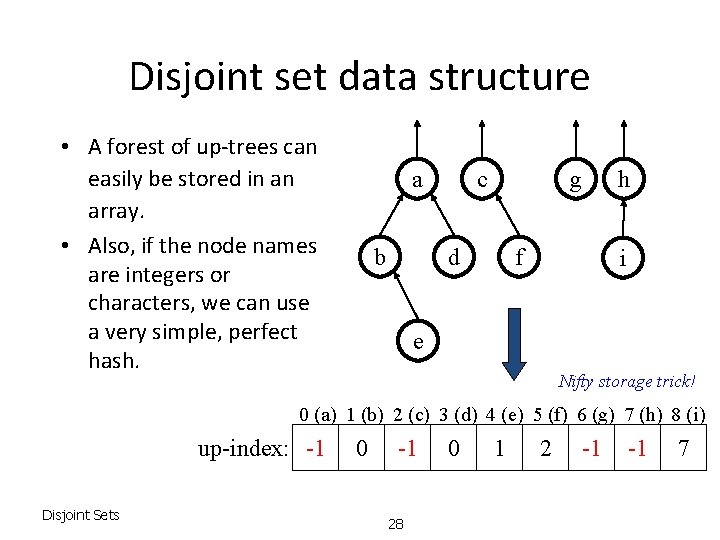
Disjoint set data structure • A forest of up-trees can easily be stored in an array. • Also, if the node names are integers or characters, we can use a very simple, perfect hash. a b c g d f h i e Nifty storage trick! 0 (a) 1 (b) 2 (c) 3 (d) 4 (e) 5 (f) 6 (g) 7 (h) 8 (i) up-index: -1 Disjoint Sets 0 -1 28 0 1 2 -1 -1 7

How can we make find cheaper? Disjoint Sets 29

Why do we need union/find? • In a maze – are the beginning and ending cells in the same group? • Is your house connected to the sewer treatment plant? Disjoint Sets 30

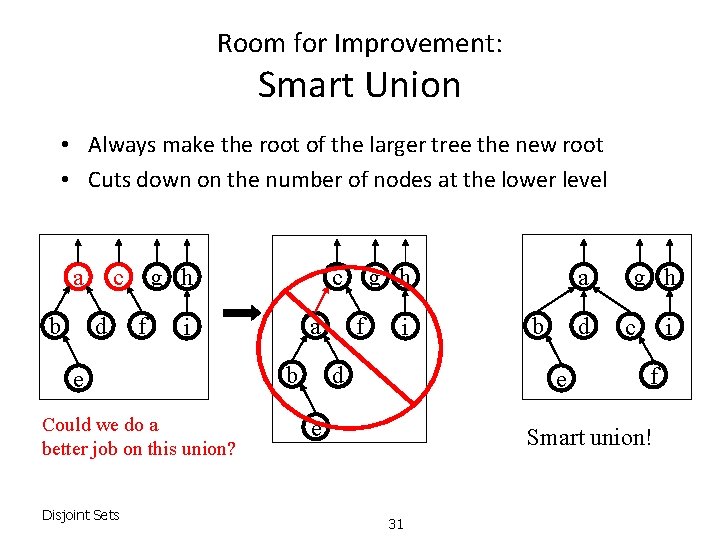
Room for Improvement: Smart Union • Always make the root of the larger tree the new root • Cuts down on the number of nodes at the lower level a b c d g h f a i e Could we do a better job on this union? Disjoint Sets c b g h f i d a b d e e g h i c f Smart union! 31

Union by size • A simple improvement is to make the smaller tree (in terms of number of nodes) a subtree of the larger, breaking ties by any method. – This is called union-by-size. – How could we keep track of the size? Disjoint Sets 32

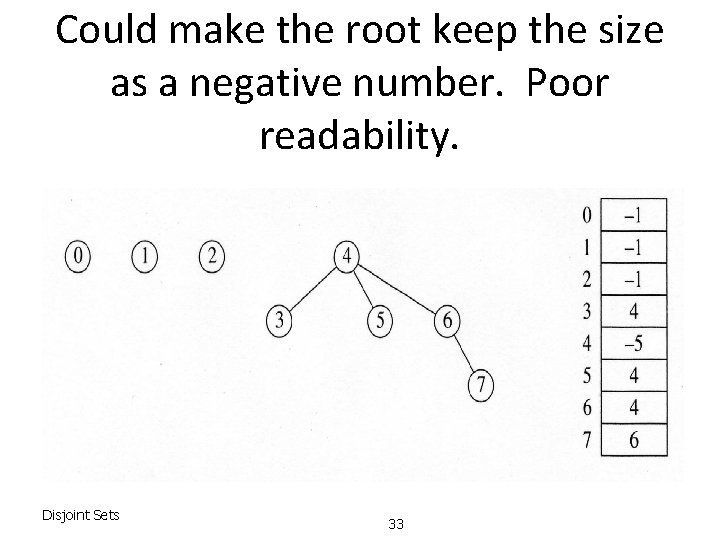
Could make the root keep the size as a negative number. Poor readability. Disjoint Sets 33

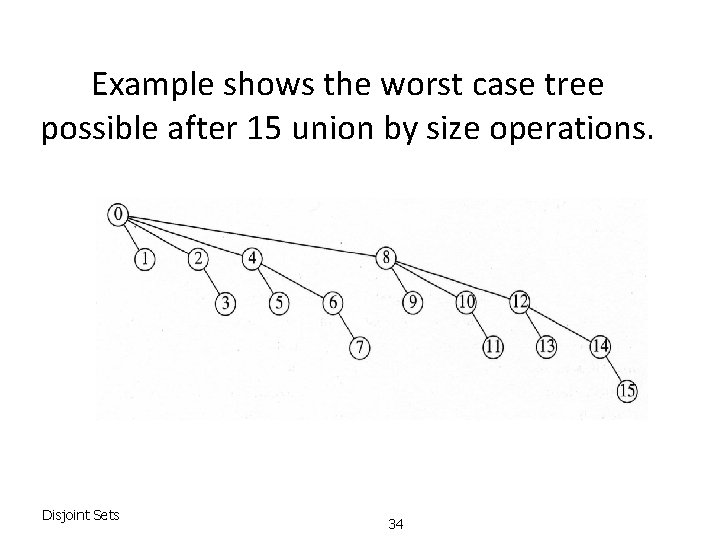
Example shows the worst case tree possible after 15 union by size operations. Disjoint Sets 34

Another idea – union by height (rank) Another implementation is union-by-height in which we keep track of the height of the trees and perform union operations by making a shallower tree a subtree of the deeper tree. Disjoint Sets 35

Union by height Code Union. Sets( int root 1, int root 2 ) { assert. Is. Root(root 1); assert. Is. Root(root 2); if (s[root 2] < s[root 1]) s[root 1]=root 2; else { if(s[root 1] == s[root 2]) s[root 1]--; // weight stored as a negative, this increases height. s[root 2] = root 1; } } //Union. Sets Disjoint Sets 36

Union by height Find Analysis • Finds with weighted union are O(max up-tree height) • But, an up-tree of height h with weighted union must have at least 2 h nodes 0 Base case: h = 0, tree has 2 = 1 node Induction hypothesis: assume true for h < h • 2 max height n and max height log n • So, find takes O(log n) Disjoint Sets A merge can only increase tree height by one over the smaller tree. So, a tree of height h -1 was merged with a larger tree to form the new tree. Each tree then has 2 h -1 nodes by the induction hypotheses for a total of at least 2 h nodes. QED. 37

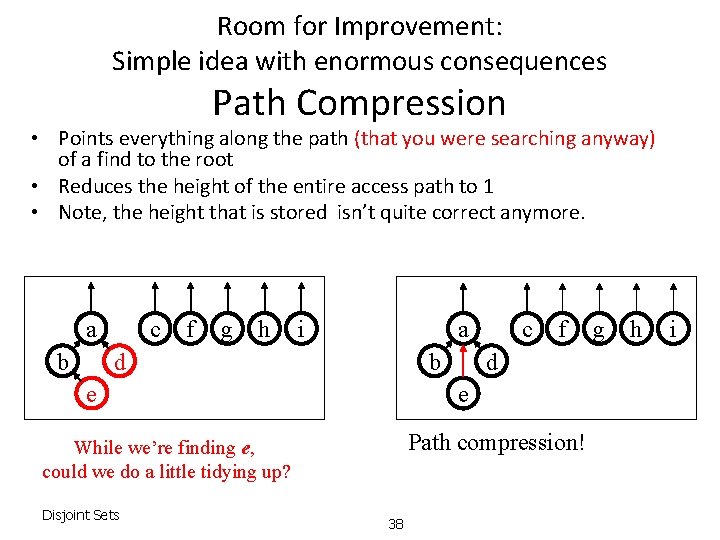
Room for Improvement: Simple idea with enormous consequences Path Compression • Points everything along the path (that you were searching anyway) of a find to the root • Reduces the height of the entire access path to 1 • Note, the height that is stored isn’t quite correct anymore. a b c f g h i a b d e f d e Path compression! While we’re finding e, could we do a little tidying up? Disjoint Sets c 38 g h i

At seats, write find with path compression Disjoint Sets 39

Analogy – Tutor Room • Suppose you need information about how to use feature F. You go to a variety of tutors. None of them know the answer, but refer you to someone else. Eventually you find the answer, and (to be nice) you inform everybody else you contacted what the answer is. Disjoint Sets 40

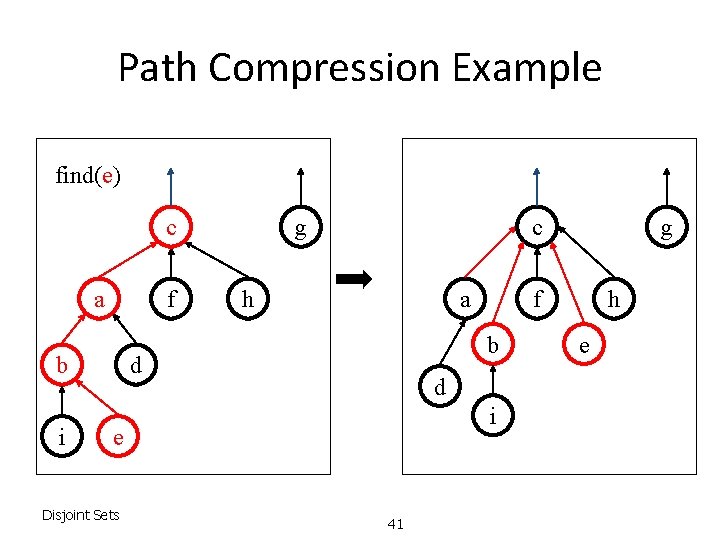
Path Compression Example find(e) c a f b i c g h a d i e Disjoint Sets f b d 41 g h e

Complexity of Weighted Union + Path Compression Ackermann created a function A(x, y) which grows very fast! Inverse Ackermann function (x, y) grows very slooooooowly … Single-variable inverse Ackermann function is called log* n How fast does log n grow? log n = 4 for n = 16 Let log(k) n = log (log … (log n))) Then, let log* n = minimum k such that log(k) n 1 How fast does log* n grow? log* n = 4 for n = 65536 log* n = 5 for n = 265536 (20, 000 digit number!) How fast does (x, y) grow? Even sloooooower than log* n (x, y) = 4 for n far larger than the number of atoms in the universe (2300) Disjoint Sets 42

Complexity of Weighted Union + Path Compression • Tarjan proved that m weighted union and find operations on a set of n elements have worst case complexity O(m (m, n)) • This is essentially amortized constant time • In some practical cases, weighted union or path compression or both are unnecessary because trees do not naturally get very deep. Disjoint Sets 43

Summary Disjoint Set Union/Find ADT • Simple ADT, simple data structure, simple code • It may make sense to have meaningful (non-arbitrary) set names • Complex complexity analysis, but extremely useful result: essentially, constant time! • Lots of potential applications – Find cycles in a structure – Dynamic connectivity(friend of a friend, maze slots, spanning tree construction) – Image segmentation by similar colored regions – Least common ancestor – Equivalence of finite state automata – Polymorphic type inference or Fortran equivalence statements – Percolation (Hoshen-Kopelman algorithm in physics) Disjoint Sets 44

One application is in the modeling of percolation or electrical conduction. If occupied cells are made of copper and unoccupied cells of glass, then a cluster is a group of electrically connected cells. Disjoint Sets 45