Data Structures and Abstractions with Java 5 th

Overview of Two Implementations • Two common implementations of the ADT graph – Array: ▪ Typically a two-dimensional array called an adjacency matrix – List: ▪ Referred to as an adjacency list. Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

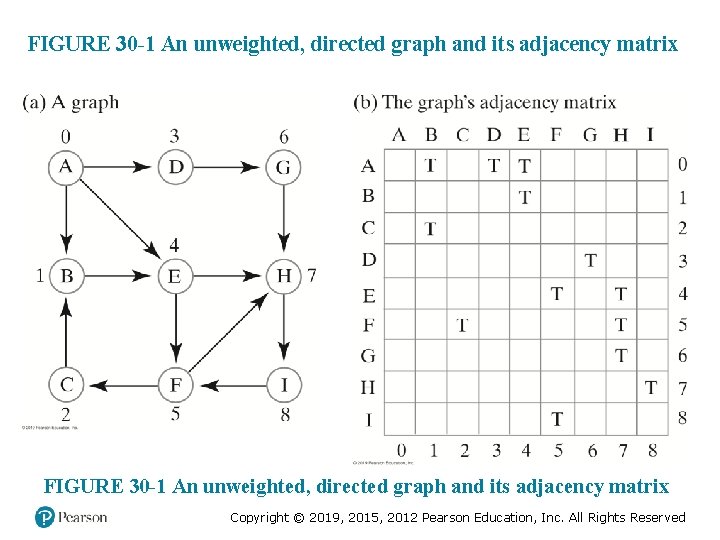
FIGURE 30 -1 An unweighted, directed graph and its adjacency matrix Copyright © 2019,

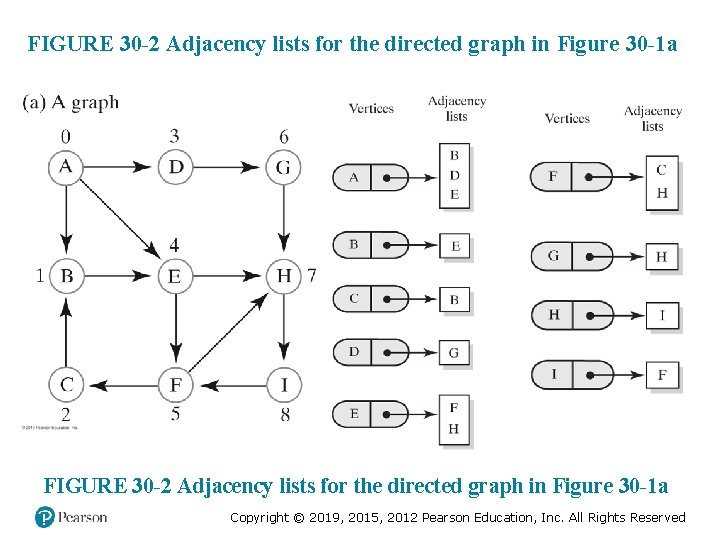
FIGURE 30 -2 Adjacency lists for the directed graph in Figure 30 -1 a

Vertices and Edges • Specifying the Class Vertex – Identify vertices – Visit vertices

Vertices and Edges — Interface (Part 1) /** An interface for a vertex in a graph. */ public interface Vertex. Interface<T> { /** Gets this vertex's label. @return The object that labels the vertex. */ public T get. Label(); /** Marks this vertex as visited. */ public void visit(); /** Removes this vertex's visited mark. */ public void unvisit(); /** Sees whether the vertex is marked as visited. @return True if the vertex is visited. */ public boolean is. Visited(); /** Connects this vertex and a given vertex with a weighted edge. The two vertices cannot be the same, and must not already have this edge between them. In a directed graph, the edge points toward the given vertex. @param end. Vertex A vertex in the graph that ends the edge. @param edge. Weight A real-valued edge weight, if any. @return True if the edge is added, or false if not. */ public boolean connect(Vertex. Interface<T> end. Vertex, double edge. Weight); LISTING 30 -1 An interface for the vertices in a graph Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Vertices and Edges — Interface (Part 2) /** Connects this vertex and a given vertex with an unweighted edge. The two vertices cannot be the same, and must not already have this edge between them. In a directed graph, the edge points toward the given vertex. @param end. Vertex A vertex in the graph that ends the edge. @return True if the edge is added, or false if not. */ public boolean connect(Vertex. Interface<T> end. Vertex); /** Creates an iterator of this vertex's neighbors by following all edges that begin at this vertex. @return An iterator of the neighboring vertices of this vertex. */ public Iterator<Vertex. Interface<T>> get. Neighbor. Iterator(); /** Creates an iterator of the weights of the edges to this vertex's neighbors. @return An iterator of edge weights for edges to neighbors of this vertex. */ public Iterator<Double> get. Weight. Iterator(); /** Sees whether this vertex has at least one neighbor. @return True if the vertex has a neighbor. */ public boolean has. Neighbor(); /** Gets an unvisited neighbor, if any, of this vertex. @return Either a vertex that is an unvisited neighbor or null if no such neighbor exists. */ public Vertex. Interface<T> get. Unvisited. Neighbor(); LISTING 30 -1 An interface for the vertices in a graph Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Vertices and Edges — Interface (Part 3) /** Records the previous vertex on a path to this vertex. @param predecessor The vertex previous to this one along a path. */ public void set. Predecessor(Vertex. Interface<T> predecessor); /** Gets the recorded predecessor of this vertex. @return Either this vertex's predecessor or null if no predecessor was recorded. */ public Vertex. Interface<T> get. Predecessor(); /** Sees whether a predecessor was recorded for this vertex. @return True if a predecessor was recorded. */ public boolean has. Predecessor(); /** Records the cost of a path to this vertex. @param new. Cost The cost of the path. */ public void set. Cost(double new. Cost); /** Gets the recorded cost of the path to this vertex. @return The cost of the path. */ public double get. Cost(); } // end Vertex. Interface LISTING 30 -1 An interface for the vertices in a graph Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

The Inner Class Edge protected class Edge { private Vertex. Interface<T> vertex; // Vertex at end of edge private double weight; protected Edge(Vertex. Interface<T> end. Vertex, double edge. Weight) { vertex = end. Vertex; weight = edge. Weight; } // end constructor protected Edge(Vertex. Interface<T> end. Vertex) { vertex = end. Vertex; weight = 0; } // end constructor protected Vertex. Interface<T> get. End. Vertex() { return vertex; } // end get. End. Vertex protected double get. Weight() { return weight; } // end get. Weight } // end Edge LISTING 30 -2 The protected class Edge, as an inner class of Vertex Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementing the Class Vertex (Part 1) /** A class of vertices for a graph. */ class Vertex<T> implements Vertex. Interface<T> { private T label; private List. With. Iterator. Interface<Edge> edge. List; // Edges to neighbors private boolean visited; // True if visited private Vertex. Interface<T> previous. Vertex; // On path to this vertex private double cost; // Of path to this vertex public Vertex(T vertex. Label) { label = vertex. Label; edge. List = new Linked. List. With. Iterator<>(); visited = false; previous. Vertex = null; cost = 0; } // end constructor /* Implementations of the vertex operations go here. . */ LISTING 30 -3 An outline of the class Vertex Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementing the Class Vertex (Part 2) protected class Edge { private Vertex. Interface<T> vertex; // Vertex at end of edge private double weight; protected Edge(Vertex. Interface<T> end. Vertex, double edge. Weight) { vertex = end. Vertex; weight = edge. Weight; } // end constructor protected Edge(Vertex. Interface<T> end. Vertex) { vertex = end. Vertex; weight = 0; } // end constructor protected Vertex. Interface<T> get. End. Vertex() { return vertex; } // end get. End. Vertex protected double get. Weight() { return weight; } // end get. Weight } // end Edge } // end Vertex Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementing the Class Vertex — method connect public boolean connect(Vertex. Interface<T> end. Vertex) { return connect(end. Vertex, 0); } // end connect public boolean connect(Vertex. Interface<T> end. Vertex, double edge. Weight). { boolean result = false; if (!this. equals(end. Vertex)) { // Vertices are distinct Iterator<Vertex. Interface<T>> neighbors = get. Neighbor. Iterator(); boolean duplicate. Edge = false; while (!duplicate. Edge && neighbors. has. Next()) { Vertex. Interface<T> next. Neighbor = neighbors. next(); if (end. Vertex. equals(next. Neighbor)) duplicate. Edge = true; } // end while if (!duplicate. Edge) { edge. List. add(new Edge(end. Vertex, edge. Weight)); result = true; } // end if return result; } // end connect Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementing the Class Vertex public Iterator<Vertex. Interface<T>> get. Neighbor. Iterator() { return new Neighbor. Iterator(); } // end get. Neighbor. Iterator The iterator Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementing the Class Vertex private class Neighbor. Iterator implements Iterator<Vertex. Interface<T>>. { private Iterator<Edge> edges; private Neighbor. Iterator() { edges = edge. List. get. Iterator(); } // end default constructor public boolean has. Next() { return edges. has. Next(); } // end has. Next public Vertex. Interface<T> next() { Vertex. Interface<T> next. Neighbor = null; if (edges. has. Next()) { Edge edge. To. Next. Neighbor = edges. next(); next. Neighbor = edge. To. Next. Neighbor. get. End. Vertex(); } else throw new No. Such. Element. Exception(); return next. Neighbor; } // end next LISTING 30 -4 The private class Neighbor. Iterator, as an inner class of Vertex Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementing the Class Vertex public boolean has. Neighbor() { return !edge. List. is. Empty(); } // end has. Neighbor public Vertex. Interface<T> get. Unvisited. Neighbor() { Vertex. Interface<T> result = null; Iterator<Vertex. Interface<T>> neighbors = get. Neighbor. Iterator(); while ( neighbors. has. Next() && (result == null) ) { Vertex. Interface<T> next. Neighbor = neighbors. next(); if (!next. Neighbor. is. Visited()) result = next. Neighbor; } // end while return result; } // end get. Unvisited. Neighbor The methods has. Neighbor and get. Unvisited. Neighbor Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementing the Class Vertex public boolean equals(Object other) { boolean result; if ((other == null) || (get. Class() != other. get. Class())) result = false; else { // The cast is safe within this else clause @Suppress. Warnings("unchecked") Vertex<T> other. Vertex = (Vertex<T>)other; result = label. equals(other. Vertex. label); } // end if return result; } // end equals The method equals Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

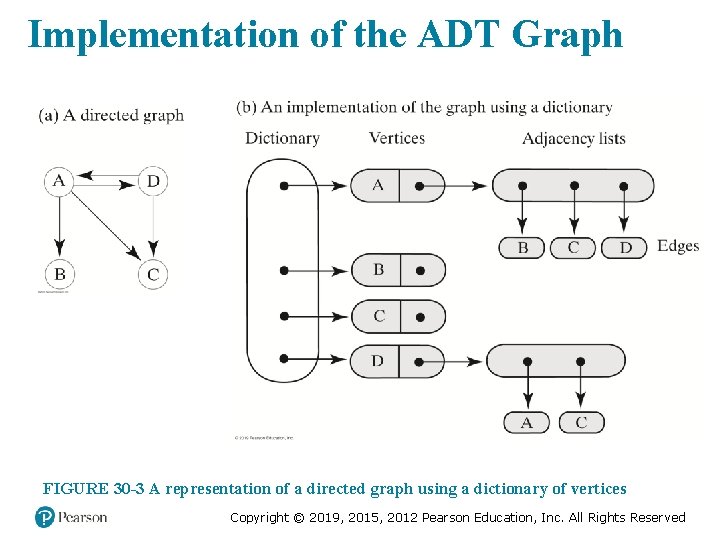
Implementation of the ADT Graph FIGURE 30 -3 A representation of a directed graph

Implementation of the ADT Graph /** A class that implements the ADT directed graph. */ public class Directed. Graph<T> implements Graph. Interface<T> { private Dictionary. Interface<T, Vertex. Interface<T>> vertices; private int edge. Count; public Directed. Graph() { vertices = new Linked. Dictionary<>(); edge. Count = 0; } // end default constructor /* Implementations of the graph operations go here. . */ } // end Directed. Graph LISTING 30 -5 An outline of the class Directed. Graph Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementation of the ADT Graph public boolean add. Vertex(T vertex. Label) { Vertex. Interface<T> add. Outcome = vertices. add(vertex. Label, new Vertex<>(vertex. Label)); return add. Outcome == null; // Was addition to // dictionary successful? } // end add. Vertex The dictionary’s method add. Vertex Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementation of the ADT Graph public boolean add. Edge(T begin, T end) { return add. Edge(begin, end, 0); } // end add. Edge public boolean add. Edge(T begin, T end, double edge. Weight) { boolean result = false; Vertex. Interface<T> begin. Vertex = vertices. get. Value(begin); Vertex. Interface<T> end. Vertex = vertices. get. Value(end); if ( (begin. Vertex != null) && (end. Vertex != null) ) result = begin. Vertex. connect(end. Vertex, edge. Weight); if (result) edge. Count++; return result; } // end add. Edge The add. Edge methods Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementation of the ADT Graph public boolean has. Edge(T begin, T end) { boolean found = false; Vertex. Interface<T> begin. Vertex = vertices. get. Value(begin); Vertex. Interface<T> end. Vertex = vertices. get. Value(end); if ( (begin. Vertex != null) && (end. Vertex != null) ) { Iterator<Vertex. Interface<T>> neighbors = begin. Vertex. get. Neighbor. Iterator(); while (!found && neighbors. has. Next()) { Vertex. Interface<T> next. Neighbor = neighbors. next(); if (end. Vertex. equals(next. Neighbor)) found = true; } // end while } // end if return found; } // end has. Edge Testing for an edge Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementation of the ADT Graph public boolean is. Empty() { return vertices. is. Empty(); } // end is. Empty public void clear() { vertices. clear(); edge. Count = 0; } // end clear public int get. Number. Of. Vertices() { return vertices. get. Size(); } // end get. Number. Of. Vertices public int get. Number. Of. Edges() { return edge. Count; } // end get. Number. Of. Edges Miscellaneous methods Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Implementation of the ADT Graph protected void reset. Vertices() { Iterator<Vertex. Interface<T>> vertex. Iterator = vertices. get. Value. Iterator(); while (vertex. Iterator. has. Next()) { Vertex. Interface<T> next. Vertex = Vertex. Iterator. next(); next. Vertex. unvisit(); next. Vertex. set. Cost(0); next. Vertex. set. Predecessor(null); } // end while } // end reset. Vertices Resetting vertices Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Efficiency of Basic Graph Operations Operation add. Vertex O(n) add. Edge O(n) has. Edge O(n) is. Empty O(1) get. Number. Of. Vertices O(1) get. Number. Of. Edges O(1) Clear O(1) FIGURE 30 -4 The performance of basic operations of the ADT graph when implemented by using adjacency lists Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Graph Algorithms — Breadth-first traversal public Queue. Interface<T> get. Breadth. First. Traversal(T origin) { reset. Vertices(); Queue. Interface<T> traversal. Order = new Linked. Queue<>(); Queue. Interface<Vertex. Interface<T>> vertex. Queue = new Linked. Queue<>(); Vertex. Interface<T> origin. Vertex = vertices. get. Value(origin); origin. Vertex. visit(); traversal. Order. enqueue(origin); // Enqueue vertex label vertex. Queue. enqueue(origin. Vertex); // Enqueue vertex while (!vertex. Queue. is. Empty()) { Vertex. Interface<T> front. Vertex = vertex. Queue. dequeue(); Iterator<Vertex. Interface<T>> neighbors = front. Vertex. get. Neighbor. Iterator(); while (neighbors. has. Next()) { Vertex. Interface<T> next. Neighbor = neighbors. next(); if (!next. Neighbor. is. Visited()) { next. Neighbor. visit(); traversal. Order. enqueue(next. Neighbor. get. Label()); vertex. Queue. enqueue(next. Neighbor); } // end if } // end while return traversal. Order; } // end get. Breadth. First. Traversal Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Graph Algorithms — Finding the shortest path (Part 1) public int get. Shortest. Path(T begin, T end, Stack. Interface<T> path) { reset. Vertices(); boolean done = false; Queue. Interface<Vertex. Interface<T>> vertex. Queue = new Linked. Queue<>(); Vertex. Interface<T> origin. Vertex = vertices. get. Value(begin); Vertex. Interface<T> end. Vertex = vertices. get. Value(end); origin. Vertex. visit(); vertex. Queue. enqueue(origin. Vertex); while (!done && !vertex. Queue. is. Empty()) { Vertex. Interface<T> front. Vertex = vertex. Queue. dequeue(); Iterator<Vertex. Interface<T>> neighbors = front. Vertex. get. Neighbor. Iterator(); while (!done && neighbors. has. Next()) { Vertex. Interface<T> next. Neighbor = neighbors. next(); if (!next. Neighbor. is. Visited()) { next. Neighbor. visit(); next. Neighbor. set. Cost(1 + front. Vertex. get. Cost()); next. Neighbor. set. Predecessor(front. Vertex); vertex. Queue. enqueue(next. Neighbor); } // end if Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved

Graph Algorithms — Finding the shortest path (Part 2) if (next. Neighbor. equals(end. Vertex)) done = true; } // end while // Traversal ends; construct shortest path int path. Length = (int)end. Vertex. get. Cost(); path. push(end. Vertex. get. Label()); Vertex. Interface<T> vertex = end. Vertex; while (vertex. has. Predecessor()) { vertex = vertex. get. Predecessor(); path. push(vertex. get. Label()); } // end while return path. Length; } // end get. Shortest. Path Copyright © 2019, 2015, 2012 Pearson Education, Inc. All Rights Reserved