CPSC 335 Geometric Data Structures in Computer Modeling

CPSC 335 Geometric Data Structures in Computer Modeling and GIS Dr. Marina L. Gavrilova Assistant Professor Dept of Comp. Science, University of Calgary, AB, Canada, T 2 N 1 N 4

Topics n n Survey of applications of computational geometry to modeling and simulation of natural processes and GIS Brief introduction to Voronoi diagrams, ROAM and progressive meshes Application to terrain modeling Application to image processing and visualization

Computational geometry n n n Originated in 1960 with invention of computers Describes algorithms and data structures for solving geometric problems with the use of computational methods Confirmed by practical implementation of methods

Areas of applicability The Monter Carlo model of a lipid bilayer in water, 8666 atoms A spectrum of computational geometry applications: n Biology n Molecular dynamics n GIS (Geographical Information Systems) n Physics n Mechanics n Chemistry

Problems in CG Problems that are addressed include: n n n n computing properties of particles arrangements, such as their volume and topology, in a general d-dimensional space testing intersections and collisions between particles finding offset surfaces (related to questions of accessibility of subregions) Solving nearest-neighbours problems Predicting time of the next collision between particles undergoing continuous motion Updating data structures accurately and efficiently Visualizing algorithms for rendering models

Subjects of study in CG n n n Spatial objects: lines, polygons, planes Operations: stored, displayed, manipulated, queried Methods: querying algorithms, optimization algorithms, visualization methods

Topological relationships n n n Adjacent Overlapping Disjoined Inclusion Neighbor Closest neighbor

Long ago… Jorge Luis Borges: "Map of a region was a size of a city, Map of an Empire was a size of a Province"

Now… Digital maps of geographical objects: n spatial, or geometric attribute (shape, location, orientation, size) in 2 D or 3 D n non-spatial attribute (descriptive)

Digital maps Geographical object: n spatial, or geometric attribute (shape, location, orientation, size) in 2 D or 3 D n non-spatial attribute (descriptive): statistic, population, force, velocity, etc.

What computer scientists are looking for: Not only a goal, but a process itself! n Data structure: both inherent and coherent n n model properties, attributed geometric data structures Ex: Surface representation n Algorithms: efficient, reliable, easy to update, portable, easy to implement, possible to visualize

Commonly used data structures in GIS Space partitioning: n Planar subdivisions (regular and irregular) n Tree-based data structure (segment trees, k-d trees, hierarchical octrees…) n Voronoi diagrams n Triangulations k cells

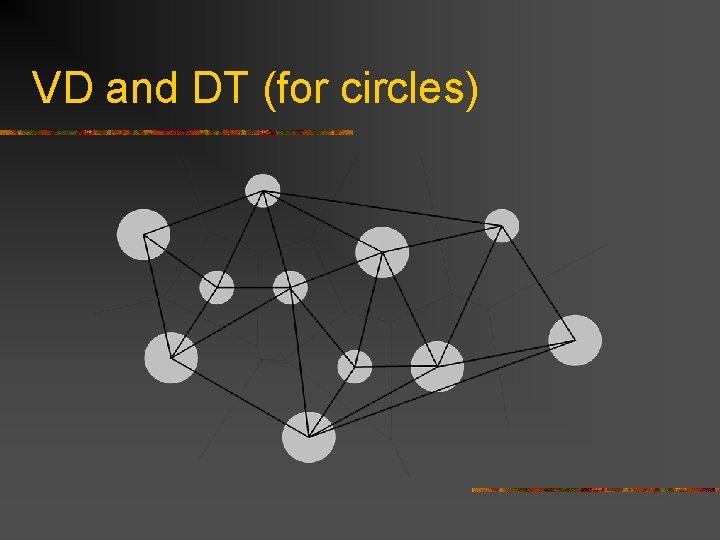
Voronoi diagram n n Given a set of N sites (points) in the plane or a 3 D space Distance function d(x, P) between point x and site P is defined according to some metric Voronoi region Vor(P) is the set of all points which are closer to P than to any other site Voronoi diagram is the union of all Voronoi regions

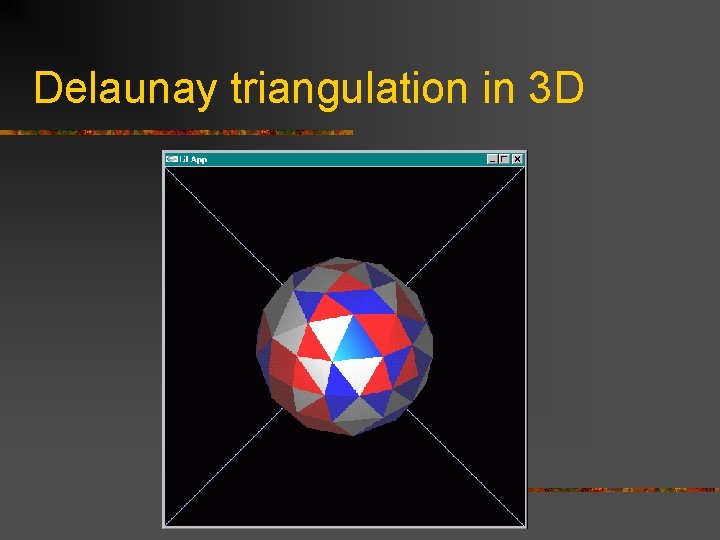
Delaunay triangulation The generalized Delaunay tessellation (DT) is the data structure, dual to the generalized VD, containing proximity information for a set S. Definition 3. A Delaunay triangulation (DT) is the straight-line dual of the Voronoi diagram obtained by joining all pairs of sites whose Voronoi regions share a common Voronoi edge [Delaunay 34]. Follows from the definition: n n If two Voronoi regions Vor(P) and Vor(Q) share an edge, then sites P and Q are connected by an edge in the Delaunay triangulation If a Voronoi vertex belongs to Vor(P), Vor(Q) and Vor(R), then DT contains a triangle (P, Q, R)

VD and DT (for circles)

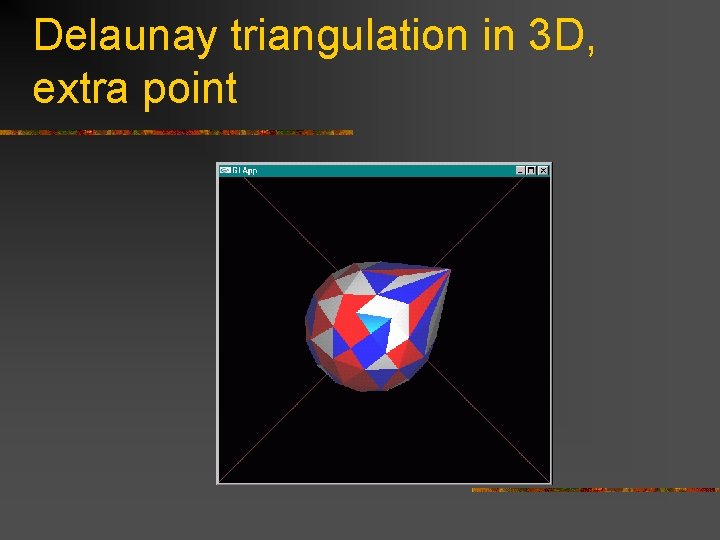
Delaunay triangulation in 3 D

Delaunay triangulation in 3 D, extra point

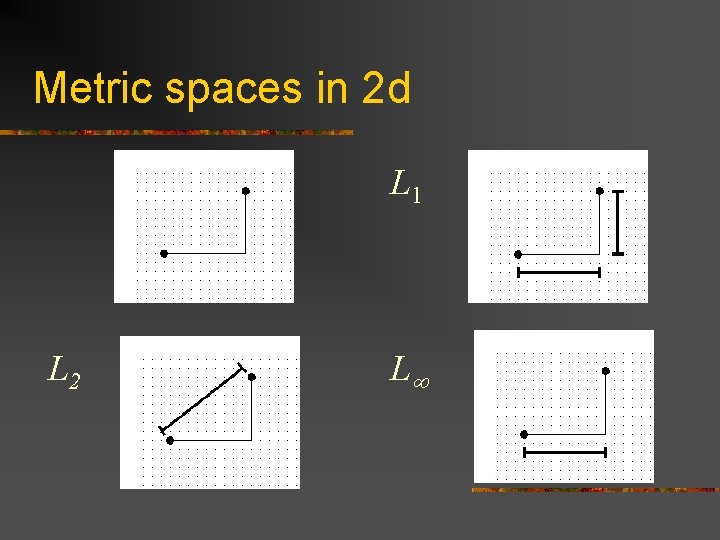
Distances: Given a set of spherical objects (sites) S in Rd. Point x from Rd is the nearest neighbor of P from S iff d(x, P) <= d(x, Q), Q from S. Euclidean metric: d(x, P) = d(x, p) - rp Manhattan metric: d(x, P) = d(x, p) - rp = |x 1 - p 1| +…+ |xd - pd|-rp Supremum metric: d(x, P) = d(x, p) - rp = max(|x 1 - p 1|…|xd - pd|) - rp Laguerre geometry: d(x, P) = d(x, p)2 - r 2 p =(x 1 - p 1)2+…(xd- pd)2 - r 2 p

Metric spaces in 2 d L 1 L 2 L

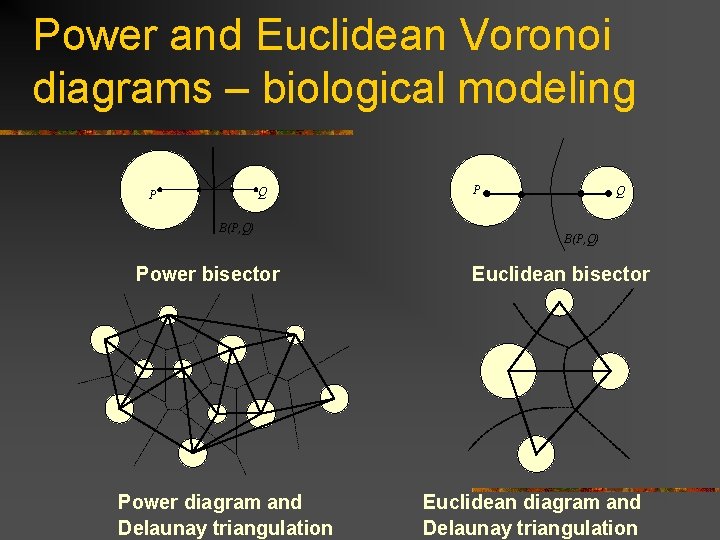
Power and Euclidean Voronoi diagrams – biological modeling Q P B(P, Q) Power bisector Power diagram and Delaunay triangulation P Q B(P, Q) Euclidean bisector Euclidean diagram and Delaunay triangulation

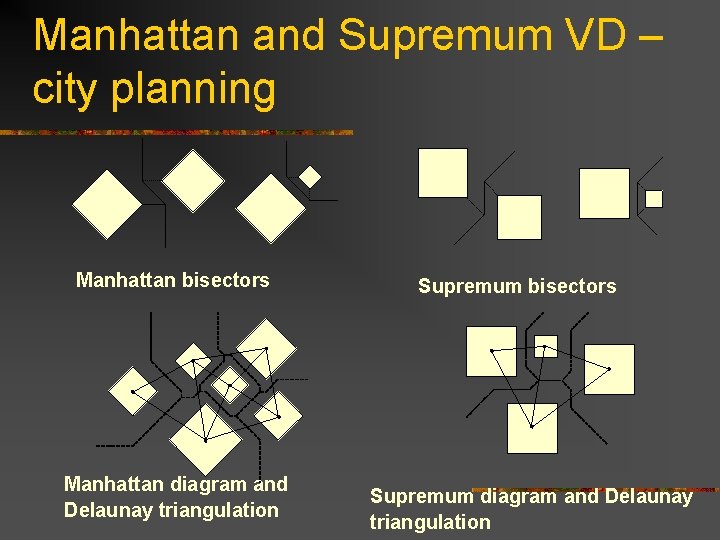
Manhattan and Supremum VD – city planning Manhattan bisectors Manhattan diagram and Delaunay triangulation Supremum bisectors Supremum diagram and Delaunay triangulation

Example of Supremum VD and DT The supremum weighted Voronoi diagram (left) and the corresponding Delaunay triangulation (right) for 1000 randomly distributed sites.

Metric spaces are used: n n In computer modeling For optimization For point patter analysis For autocorrelation analysis

3 D Terrain Rendering n n Involves transformation of GIS data sources into a 3 D coherent system Convert 2 D map layers to 3 D Using rendering methods to project the 3 D data back to 2 D Manipulate Camera and animation methods to obtain perspective view

Sourcing data from real world

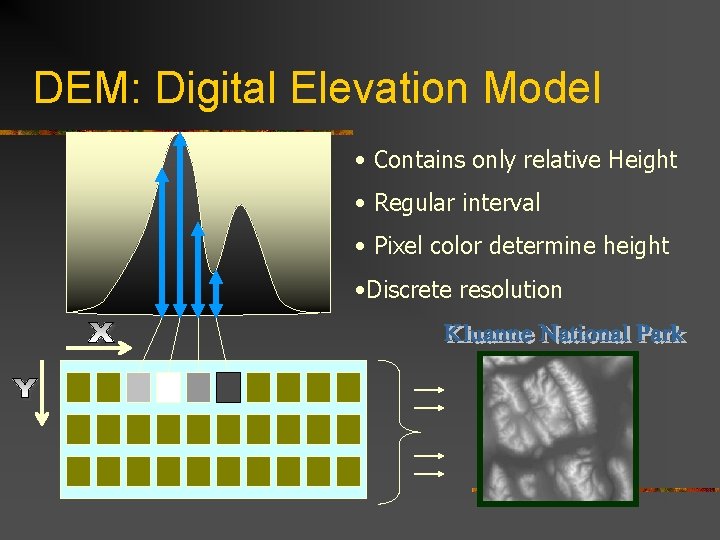
DEM – Digital Elevation Models n n n Finite representation of an abstract modeled space. Represent a function of 2 D space: temperature, pressure, etc. Exist in sampled points in space, other points obtained by interpolation.

DEM: Digital Elevation Model • Contains only relative Height • Regular interval • Pixel color determine height • Discrete resolution

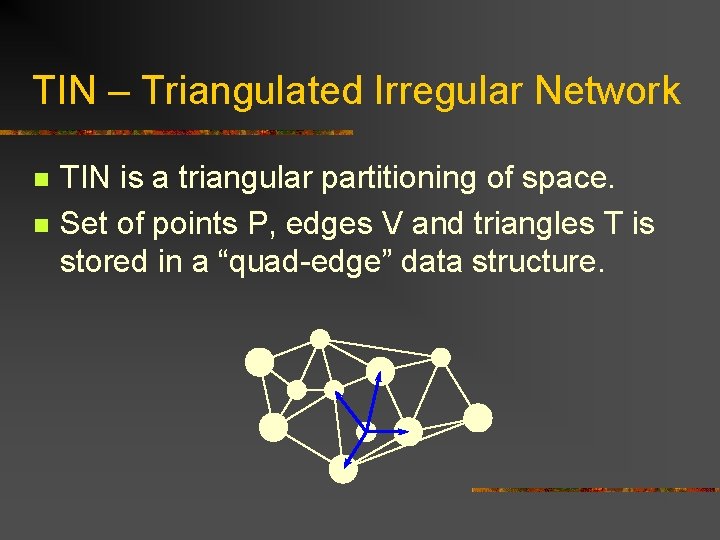
TIN – Triangulated Irregular Network n n TIN is a triangular partitioning of space. Set of points P, edges V and triangles T is stored in a “quad-edge” data structure.

Tessellation in terrain modeling n Tessellation is a cellular decomposition of the plane (space).

Non-Photo-Realistic Real-time 3 D Terrain Rendering • Uses DEM as input of the application • Generates frame coherent animated view in real-time • Uses texturing, shades, particles etc. for layer visualization

Real-time terrain rendering n n n Uses a graphics Engine/Library Central focus on efficient mesh representation View coherence and frame rate constancy Limited/Variable Level of Detail Speed optimization Representing layer data as textures or particles

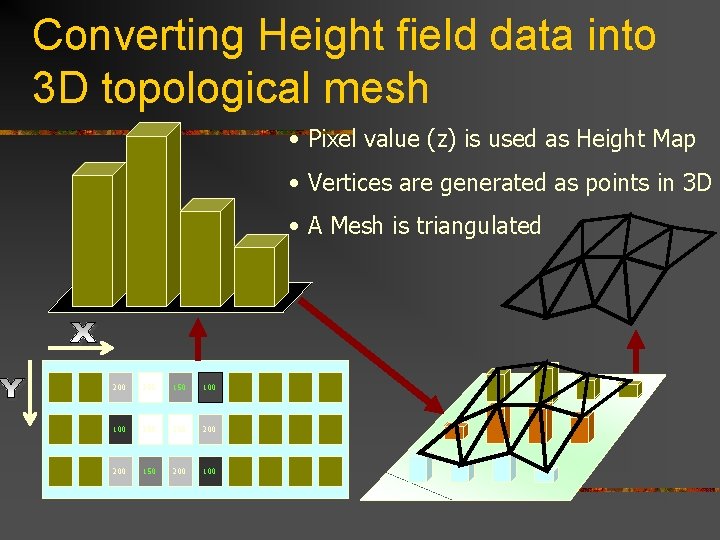
Converting Height field data into 3 D topological mesh • Pixel value (z) is used as Height Map • Vertices are generated as points in 3 D • A Mesh is triangulated 200 255 150 100 255 200 150 200 100

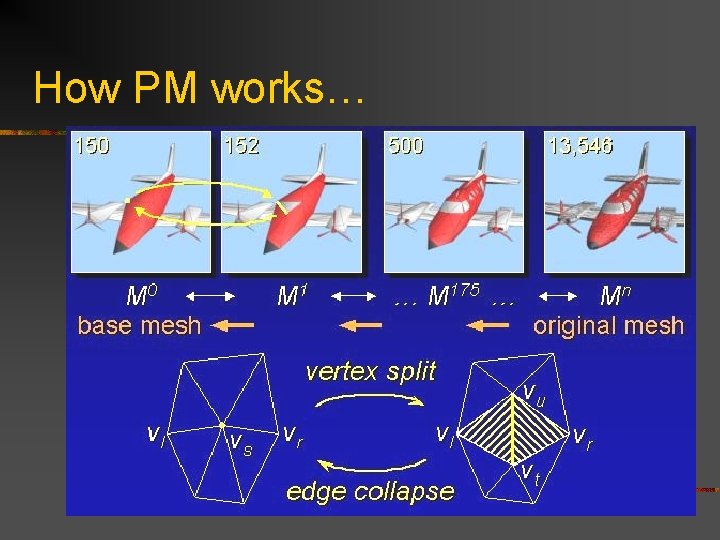
Mesh Representation n Goals: n Representations: n Speed n Progressive Meshes n Quality n n Constancy ROAM: Real-time Optimally Adapting Mesh

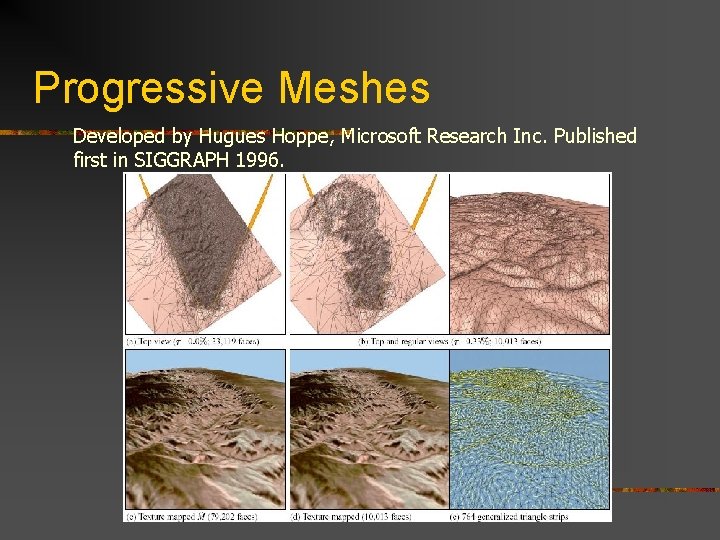
Progressive Meshes Developed by Hugues Hoppe, Microsoft Research Inc. Published first in SIGGRAPH 1996.

How PM works…

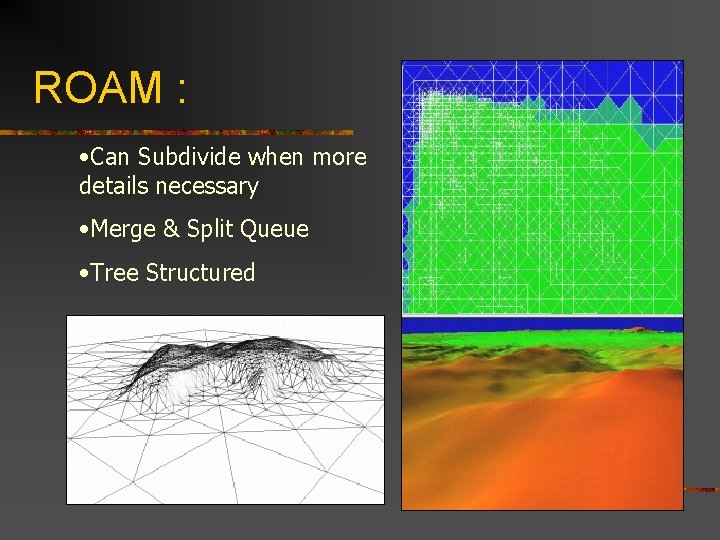
ROAM : • Can Subdivide when more details necessary • Merge & Split Queue • Tree Structured

Photo Realistic 3 D Terrain

Conclusions n Computational geometry methods find a variety of applications in GIS and other areas: for underlying data structures, algorithm implementation, querying, visualization, statistical analysis and optimization.